ANALYSIS AND TUNING OF A MULTIVARIABLE PLANT: APPLICATION OF THE INTERNAL MODEL CONTROL (IMC) TUNING METHOD.
REGISTRO DOI: 10.69849/revistaft/ar10202411220855
Lucas Amorim Barros¹;
Prof. Me. Stênio Sousa de Coelho².
Resumo
O estudo explora a análise e sintonia de uma planta multivariável de velocidade e temperatura para a implementação de um controlador PI. Para isso, aplicou-se o método de Controle por Modelo Interno (IMC), visando otimizar o desempenho do processo. A modelagem do sistema foi realizada por meio de regressão de Ridge, devido à sua capacidade de lidar com dados multivariáveis e a colinearidade entre eles. Foram testadas abordagens de sintonia conservadora e agressiva para verificar a eficiência do método em processos multivariáveis. Os critérios de avaliação incluíram “overshoot”, tempo de subida e índices de integral do erro. Os resultados visam avaliar a viabilidade de métodos simplificados na busca de uma performance eficiente e de baixo esforço de sintonia em sistemas de controle industriais complexos. O método IMC apresentou um resultado satisfatório em regime permanente, porém não conseguiu extrair a potencialidade da planta de ação de aquecimento e resfriamento rápidos e a sintonia com uma ação agressiva apresentou melhores índices de desempenho devido as características intrínsecas do processo controlado.
Palavras-chave: Controle por Modelo Interno. Controlador PI. Regressão de Ridge. Multivariáveis. Métodos de Sintonia.
1 INTRODUÇÃO
Os sistemas de controle desempenham um papel fundamental na sociedade contemporânea, estando presentes em uma ampla variedade de aplicações. Desde o acionamento de foguetes e a decolagem de ônibus espaciais rumo à órbita terrestre, até processos industriais automatizados, como a usinagem de peças metálicas assistida por jatos de água de resfriamento, os sistemas de controle estão integrados em diversas operações de alta precisão. Além disso, exemplos como veículos autônomos que distribuem materiais em estações de trabalho em oficinas aeroespaciais ilustram como esses sistemas contribuem para a automação e otimização de processos complexos em diferentes setores (NISE, 2012). Essas tecnologias representam apenas uma fração das inúmeras possibilidades de sistemas controlados automaticamente que podem ser desenvolvidas.
As indústrias inseridas em mercados altamente competitivos enfrentam a necessidade de aprimorar continuamente a produtividade de suas plantas industriais. Nesse contexto, uma área tecnológica crucial para promover a eficiência das unidades produtivas é a de controle, automação e otimização de processos. Tais tecnologias visam alcançar diversos benefícios, incluindo a melhoria da qualidade dos produtos, a minimização de retrabalhos, o aumento da confiabilidade dos sistemas e a redução da carga de trabalho dos operadores, liberando-os de atividades manuais e repetitivas (CAMPOS & TEXEIRA, 2010).
Com base nessas circunstâncias, foi somente no início do século XX que o controlador PID, como o conhecemos atualmente, surgiu. Grande parte da teoria fundamental utilizada na melhoria do desempenho de sistemas de controle automático pode ser atribuída a Nicholas Minorsky, um engenheiro russo nascido em 1885. Foi seu trabalho teórico, aplicado à automação na condução de navios, que resultou no desenvolvimento dos controladores proporcional, integral e derivativo (PID), conhecidos também como controladores de três modos. Esses controladores são amplamente estudados e utilizados em diversas áreas da engenharia (NISE, 2012).
Inicialmente, os ajustes desses parâmetros eram realizados de maneira empírica, com base no método de tentativa e erro. No entanto, com o crescente uso industrial do controle automático, os estudiosos Ziegler e Nichols (1942) propuseram um método sistemático para a sintonia eficiente e rápida dos controladores PID, visando aplicá-los em uma variedade de plantas. Esse método revolucionou a forma de ajustar os parâmetros do controlador e permitiu sua ampla adoção nas indústrias da época, facilitando a comercialização de soluções automatizadas e otimizadas para o controle de processos em diferentes setores.
Atualmente, o controlador PID permanece como a tecnologia predominante na indústria, com mais de 90% das malhas de controle sendo do tipo PI ou PID (ÅSTROM & HAGGLUND, 2001). No estudo de Desborough e Miller (2002), destaca-se que uma grande parte desses controladores na indústria apresenta desempenho aquém do esperado. Os autores identificam vários fatores para essa ineficiência, como a ausência de monitoramento e manutenção contínua dos parâmetros do controlador. Em seus estudos, foram também evidenciadas as principais demandas dos responsáveis por esses controladores, que incluem: a) tornar a tecnologia simples e intuitiva de usar; b) facilitar o acesso rápido e direto a informações importantes; e c) proporcionar uma configuração e manutenção descomplicadas.
Para a sintonia de uma planta de controle multivariável de velocidade e temperatura, utilizou-se o método de Controle por Modelo Interno (IMC), uma abordagem amplamente reconhecida por sua simplicidade e eficácia na determinação de parâmetros do controlador. O método IMC baseia-se na modelagem da inversa do sistema, o que permite que os parâmetros de sintonia sejam calculados diretamente a partir do modelo do processo, facilitando ajustes específicos ao comportamento desejado (MORARI & ZAFIRIOU, 1989). Nesse contexto, aplicou-se a regressão de Ridge para modelar a dinâmica do sistema, uma técnica robusta para evitar problemas de multicolinearidade e ajustar modelos multivariáveis complexos, especialmente em processos com dados ruidosos ou altamente correlacionados (HOERL & KENNARD, 1970).
Adotaram-se duas abordagens de sintonia para o controlador utilizando método de Controle por Modelo Interno (SKOGESTAD, 2003): uma abordagem conservadora, focada em estabilidade e robustez, e uma abordagem mais agressiva, que visa uma resposta rápida e um menor tempo de acomodação, ambas amplamente descritas na literatura como técnicas recomendadas para diferentes objetivos de controle.
O objetivo deste estudo é avaliar a viabilidade de métodos simplificados de controle, como o IMC, em processos multivariáveis, e investigar se tais métodos podem garantir uma performance ótima com baixo esforço de sintonia. Para tanto, os critérios de desempenho utilizados serão os índices de avaliação padrão de controladores PID, como “overshoot”, tempo de subida e índices de integral do erro, incluindo IAE (Integral of Absolute Error) e ITAE (Integral of Time-weighted Absolute Error), assim como a análise da dinâmica da planta sob diferentes condições de sintonia. Esses critérios permitirão verificar se a metodologia aplicada é eficaz para manter a estabilidade e alcançar uma resposta dinâmica adequada ao sistema multivariável de controle de velocidade e temperatura, promovendo, assim, uma performance robusta e eficiente.
2 FUNDAMENTAÇÃO TEÓRICA
O referencial teórico deste estudo apresenta os conceitos fundamentais necessários para desenvolver uma compreensão dos processos abordados. Estruturado em subtópicos, esse referencial visa promover um fluxo lógico, facilitando a compreensão dos processos de identificação e sintonia da planta de controle. Ao explorar fundamentos teóricos e abordagens específicas para controle de processos, com o objetivo de propiciar uma base sólida que orienta a análise e aplicação prática das técnicas propostas ao longo do artigo.
2.1 Regressão de Ridge
A análise de regressão é uma das técnicas mais eficazes para observar dados multifacetados em diversos campos da ciência. É amplamente reconhecido que os estimadores de mínimos quadrados (MMQ) são utilizados em modelos lineares, pois são imparciais e apresentam variação insignificante. No entanto, esses estimadores podem resultar em conclusões insatisfatórias quando os dados apresentam colinearidade (SALEH; ARASHI; KIBRIA, 2019). Essa limitação compromete a precisão das estimativas e a interpretação dos resultados, tornando fundamental a adoção de métodos alternativos, como a regressão de Ridge, nesses contextos. A colinearidade, refere-se à existência de relações quase lineares entre os regressores, preditores ou variáveis de entrada exógenas.
A regressão de Ridge é uma técnica de regularização que é amplamente utilizada na modelagem estatística, especialmente quando se trabalha com dados que apresentam colinearidade. Desenvolvida por Hoerl e Kennard (1970), a essa regressão busca minimizar a soma dos erros quadráticos, mas com a adição de uma penalidade que é proporcional ao quadrado da magnitude dos coeficientes da regressão. Essa abordagem não apenas melhora a precisão das estimativas, mas também contribui para a estabilidade do modelo, especialmente em cenários onde o número de variáveis preditivas é comparável ou superior ao número de observações. É descrito em sua forma matricial pela equação a seguir.
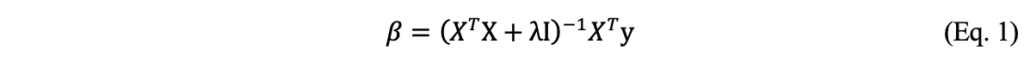
Os coeficientes estimados no modelo são representados por “β”. A matriz das variáveis preditoras é denotada por “X”, enquanto “XT” representa a matriz transposta de “X”, O vetor “y” contém as variáveis dependentes, que são os valores que o modelo tenta prever. A matriz identidade, denotada por “I”, é adicionada ao termo de regularização para garantir que a matriz “(XTX + λI)” seja invertível. O parâmetro de regularização “λ” controla a quantidade de penalização aplicada aos coeficientes, com valores maiores resultando em uma maior regularização, o que reduz a variância, mas pode aumentar o viés. O ajuste do valor de “λ” permite controlar o grau de penalização aplicado, e esse parâmetro pode ser otimizado por meio de validação cruzada para melhorar o desempenho do modelo (TIBSHIRANI, 1996).
2.2 Função de Transferência
A função de transferência descreve como uma determinada entrada é dinamicamente transferida para a saída do sistema (AGUIRRE, 2015). Em controle de sistemas, a função de transferência é utilizada para analisar e projetar controladores, pois permitem prever o comportamento da planta a diferentes entradas sem a necessidade de realizar experimentos diretos.
A identificação de uma função de transferência pode ser feita a partir de modelos de regressão, utilizando dados experimentais para ajustar uma estrutura matemática predefinida. Ljung (1999) descreve que métodos de regressão, como a regressão Ridge, são úteis para ajustar funções que descrevem a dinâmica do sistema com uma representação precisa. Esse ajuste permite obter uma função de transferência que descreve o sistema por meio de um conjunto de parâmetros identificados empiricamente, que expressam a relação entre as variáveis de entrada e saída ao longo do tempo.
A função de transferência encontrada utilizando dados discretos podem ser transformadas para uma função no tempo continuo. Para Åström e Wittenmark (2011) a forma mais simples de fazer uma reconstrução de um sinal de dados amostrados é deixar a saída do sistema constante até que o próximo valor seja obtido. Nesse processo, a retenção do sinal da saída gera uma aproximação do sinal contínuo original ao invés de uma transição suave, o sinal reconstruído “salta” de um nível para outro a cada nova amostra. Entre duas amostras consecutivas, o valor do sinal reconstruído é constante, formando degraus em vez de uma linha contínua ou curva suave. O processo citado é denominado como Segurador de Ordem Zero(ZOH), a expressão “ordem zero” indica que, entre os pontos de amostragem, o sinal é um polinômio de ordem zero.
No domínio do tempo continuo, o ZOH é representado por uma função de transferência, que é usada para transformar um sinal discreto para uma representação continua expressa na Eq. 2.
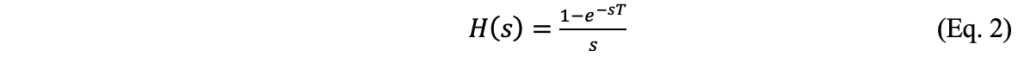
2.3 Controlador PID
O controlador Proporcional-Integral-Derivativo é amplamente reconhecido como o algoritmo de controle mais utilizado na indústria. Sua popularidade deve-se, em grande parte, à simplicidade na configuração dos parâmetros, o que permite alcançar um desempenho satisfatório em diversas aplicações (CAMPOS & TEXEIRA, 2010). Essa facilidade de ajuste e a capacidade de adaptar-se a diferentes processos tornam o PID uma solução robusta e versátil, ideal para garantir a estabilidade e a precisão em sistemas de controle industrial.
Os controladores de três modos calculam inicialmente o erro do processo, que corresponde à diferença entre a saída real do sistema e o valor desejado, denominado “setpoint”. A partir desse erro, o controlador gera um sinal de controle para minimizar essa diferença e, assim, estabilizar o sistema (CAMPOS & TEXEIRA, 2010). O algoritmo PID utiliza o erro em três componentes distintos – o termo proporcional, o integral e o derivativo – que, juntos, produzem um sinal a variável manipulada. O algoritmo do controlador PID é descrita matematicamente pela Eq. 3:
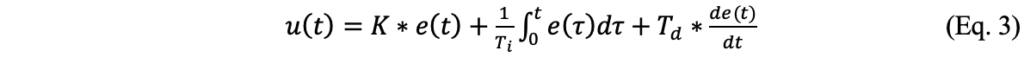
Sabe-se que o “y” é a variável observado do processo, “r” é a variável de referência ou “setpoint”, “u” é o sinal de controle e “e” é o erro de controle (e = r – y). Dessa forma, o sinal de controle é o somatório de três termos : o termo proporcional ao erro, o termo proporcional à integral do erro e o termo proporcional à derivada do erro. Os parâmetros do controlador são o ganho “K”, o tempo integral “Ti” e o tempo derivativo “Td”.
O termo proporcional é responsável por gerar uma resposta imediata ao erro. A intensidade dessa ação é ajustada pelo ganho “K”. Um valor elevado de “K” resulta em uma resposta mais rápida, mas pode levar o sistema a oscilações se o ganho for excessivo (OGATA, 2010). O termo integral acumula o erro ao longo do tempo, corrigindo desvios persistentes e eliminando-o em regime permanente. Essa componente é ajustada pelo tempo integral “Ti” e um valor menor de “Ti” resulta em uma correção mais rápida, mas pode aumentar a tendência a oscilações (CAMPOS & TEXEIRA, 2010). Por fim, o termo derivativo antecipa o comportamento futuro, reagindo à taxa de variação do erro. Essa ação é modificada pelo tempo derivativo “Td”. A inclusão da ação derivativa melhora a estabilidade do sistema e reduz o “overshoot”, pois fornece uma previsão dos desvios com base na sua taxa de mudança (ÅSTRÖM & HÄGGLUND, 1995).
Além disso, é importante destacar que a combinação das ações do controlador PID pode resultar em diferentes tipos de controladores. Por exemplo, a combinação da ação proporcional ao erro com a ação integral forma um controlador do tipo “PI”, enquanto a combinação da ação proporcional com a ação derivativa resulta em um controlador do tipo “PD”. Por fim, a ação proporcional ao erro isoladamente configura um controlador do tipo “P”. A escolha do controlador adequado deve ser baseada no funcionamento da planta de controle e nas características específicas do sistema a ser regulado.
2.4 Critérios de Desempenho
O desempenho de um controlador PID é avaliado por meio de critérios quantitativos que indicam a precisão, estabilidade e resposta do sistema a distúrbios ou alteração de “setpoint”. Dentre os principais critérios de desempenho, destacam-se o Erro Absoluto Integrado (IAE), o Erro Quadrático Integrado (ISE), o Erro Absoluto Integrado e Ponderado pelo Tempo (ITAE), além de outros parâmetros como o “overshoot”, o tempo de subida e o tempo de acomodação.
Alguns critérios baseados na resposta temporal são fundamentais para avaliar o desempenho de controladores. Um deles é o “overshoot”, que indica o valor máximo que a resposta do sistema ultrapassa o valor de referência antes de se estabilizar. Outro critério importante é o tempo de subida, que representa o tempo necessário para que a resposta do sistema atinja e permaneça dentro de uma faixa de tolerância, geralmente de ±5%, ou ±1% em aplicações que exigem maior precisão. Por fim, o tempo de acomodação mede o período necessário para que a resposta do sistema se estabilize dentro de uma margem de tolerância em torno do valor de referência, refletindo a capacidade de atingir a estabilidade desejada (SEBORG & MELLICHAMP, 2011).
Além dos critérios tradicionais, são amplamente utilizados índices de desempenho baseados em erros integrados, os quais permitem uma avaliação precisa da resposta do sistema em relação ao seu valor de referência ao longo de uma janela de tempo específica. Esses índices são calculados acompanhando a trajetória da variável controlada em comparação ao “setpoint” desejado, oferecendo uma análise detalhada do comportamento do sistema (CAMPOS & TEXEIRA, 2010).
O Erro Absoluto Integrado (IAE) representa a soma do valor absoluto do erro ao longo do tempo. Já o Erro Quadrático Integrado (ISE) eleva o erro ao quadrado antes da integração, o que resulta em uma penalização mais intensa para desvios maiores, priorizando, assim, uma resposta rápida e precisa. Por outro lado, o Erro Absoluto Integrado e Ponderado pelo Tempo (ITAE) pondera o erro em função do tempo, aplicando maior penalização a erros persistentes e minimizando oscilações prolongadas. Essa abordagem se destaca especialmente para sistemas que exigem estabilidade a longo prazo (SEBORG & MELLICHAMP, 2011). Tais índices de desempenho são descritos pela Tabela 1.
Tabela 1 – Índices de desempenho para avaliação de controle em malha fechada.

2.5 Atraso de Transporte
O atraso no tempo ocorre em sistemas de controle quando há uma diferença entre o comando de resposta e o início da resposta na saída do sistema (NISE, 2012). Por exemplo, considere um sistema de ventilação em que o ar condicionado é acionado para resfriar uma área específica. Embora o comando para resfriamento tenha sido dado, o ar frio leva um tempo para circular e alcançar o ambiente. Esse intervalo entre o acionamento do sistema e o início do resfriamento efetivo em uma área distante representa o atraso no tempo. É importante observar que esse atraso não se refere ao tempo necessário para o sistema alcançar a temperatura desejada, mas sim ao período em que ainda não há mudança perceptível na saída.
De maneira análoga, os sistemas de controle sem atraso de transporte são aqueles em que a resposta do sistema ocorre muito rápido, cuja a dinâmica é desprezível, após a aplicação de um comando (GARCIA, 2017). Em termos práticos, podemos considerar um sistema como sem atraso de transporte quando a dinâmica do processo é suficientemente rápida em comparação ao tempo necessário para que a ação do controlador se manifeste na saída. Isso ocorre geralmente em sistemas que possuem uma inércia mínima e onde as respostas não são influenciadas por fatores externos ou por variações significativas no ambiente de operação.
2.6 Sintonia de Controladores PID
O processo de encontrar e selecionar parâmetros do controlador que garantam a especificação de desempenho é denominada de sintonia do controlador (OGATA, 2010). A aplicação de métodos de sintonia, conforme autores como Ogata (2010) e Åström e Hägglund (1995), demonstra que a escolha de métodos depende do tipo de sistema em controle e das exigências de performance, como o tempo de subida, tempo de estabilização, “overshoot” e erro em regime permanente. Dessa forma, a sintonia de controladores PID permanece um campo dinâmico, contribuindo continuamente para a eficiência e a precisão em processos industriais, com perspectivas de otimização crescente conforme novas tecnologias e métodos de análise são incorporados.
Na prática, a sintonia de controladores é frequentemente realizada por tentativa e erro, um processo que pode ser demorado. Dessa forma, contar com boas estimativas preliminares dos parâmetros do controlador é desejável, pois facilita e agiliza o processo de ajuste. Essas estimativas iniciais podem ser baseadas na experiência prévia com sistemas de controle similares, o que oferece uma base aproximada para a configuração do controlador. Quando se possui um modelo matemático do sistema, é possível aplicar métodos de projeto fundamentados na teoria de controle para definir os parâmetros do controlador de maneira mais precisa. No entanto, mesmo nesses casos, ajustes em campo podem ser necessários para garantir a sintonia fina, especialmente quando o modelo matemático não representa perfeitamente as dinâmicas reais do sistema (GARCIA, 2017).
Em 1942, os engenheiros John G. Ziegler e Nataniel B. Nichols, da Taylor “Instrument Company”, desenvolveram os primeiros métodos formais de sintonia para controladores de três modos. Antes disso, os ajustes eram realizados apenas por tentativa e erro. A motivação por trás do desenvolvimento desses métodos foi a necessidade de Ziegler, do setor comercial, de promover a linha recém-lançada de controladores “Fulscope”. Em colaboração com Nichols, da equipe de pesquisa, ele buscou estabelecer uma abordagem prática para sintonizar controladores PID, incentivando assim o uso e a venda dos produtos da empresa (CAMPOS & TEIXEIRA, 2010).
Segundo Garcia (2017), os métodos de sintonia para controladores PID lineares são classificados em três principais categorias, baseadas nas técnicas empregadas em sua formulação. A primeira categoria é o método de tentativa e erro, que envolve ajustes diretamente no campo após a instalação do controlador, permitindo adaptações finas em condições reais. A segunda abrange métodos que utilizam relações de ajuste, podendo ocorrer em malha fechada ou aberta. Em malha fechada, destacam-se as Oscilações Contínuas de Ziegler e Nichols e o método de Tyreus e Luyben; em malha aberta, incluem-se os métodos de Chien, Hrones e Reswick (CHR) e o de Cohen e Coon. A terceira categoria compreende métodos de projeto fundamentados em um modelo do processo, como a Síntese Direta (ou Sintonia Lambda) e o Controle por Modelo Interno (IMC).
2.6.1 Sintonia pelo Método da Síntese Direta e Controle por Modelo Interno.
A sintonia pelo método da Síntese Direta é uma metodologia que utiliza o modelo inverso do processo controlado, associada ao cancelamento de polos e zeros, com o objetivo de atingir o desempenho desejado em malha fechada. Essa abordagem é a mesma utilizada pelo método IMC (Internal Model Control), e ambos são comumente referidos como técnicas de Sintonia Lambda, termo amplamente utilizado para classificar métodos nos quais a velocidade de resposta da malha fechada é um parâmetro ajustável. Em contrapartida de definir a localização dos polos em malha fechada, a sintonia lambda permite que a velocidade de resposta seja controlada diretamente. Esse tipo de sintonia é particularmente eficaz para sistemas de controle rápido e auxilia na redução de oscilações indesejadas (GARCIA, 2017).
Dahlin (1968) foi o pioneiro a discutir a ideia do controle de desempenho a partir de um valor de lambda em malha fechada. O parâmetro lambda foi inicialmente proposto como uma forma de controlar a velocidade de resposta do sistema, ajustando diretamente o tempo de resposta sem a necessidade de se especificar a localização exata dos polos do sistema. Essa abordagem se baseia na ideia de que o desempenho do controlador pode ser ajustado de maneira mais intuitiva e eficiente, simplesmente definindo um valor para o parâmetro lambda, que está relacionado ao comportamento transiente da malha fechada, como o tempo de subida e a amplitude das oscilações.
Os pesquisadores Rivera, Morari e Skogestad (1986) desenvolveram o método IMC para a sintonia de controladores PID. Eles aplicaram essa metodologia a diferentes dinâmicas de processos e estabeleceram uma abordagem sistemática para a sintonia de controladores, levando em consideração as características específicas de cada tipo de sistema. No caso de sistemas de primeira ordem sem atraso de transporte, a equação proposta determina um controlador PI e é apresentada a seguir, conforme descrito na Tabela 2.
Tabela 2 – Sintonia PID para sistemas de primeira ordem sem tempo morto.
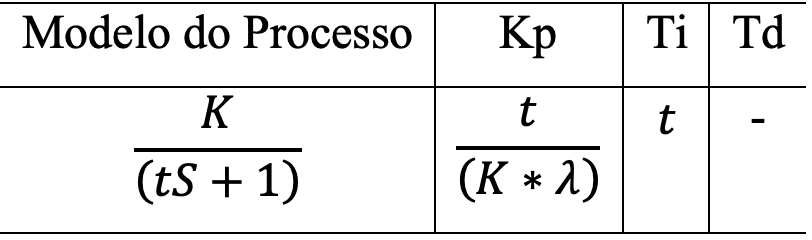
Garcia (2017) destaca que, para controladores com sintonia lambda, valores menores de “λ” resultam em uma ação de controle mais rápida, o que aumenta o ganho proporcional (Kp) e possibilita um retorno mais veloz ao valor de referência. Em contrapartida, valores mais altos de “λ” proporcionam respostas mais lentas, favorecendo a estabilidade ao reduzir variações na variável manipulada. De acordo com Teixeira e Campos (2010), uma abordagem conservadora para essa sintonia consiste em definir “λ” como equivalente à constante de tempo dominante do processo. Essa prática é recomendada, especialmente em sistemas com alta não-linearidade ou modelagem imprecisa, já que reduz potenciais erros associados às incertezas no modelo de controle.
2.7 Estruturas de Controle.
Pode-se classificar os sistemas de acordo com o número de variáveis de entrada e saída. O sistema de controle mais básico é o SISO (Single Input, Single Output), que utiliza uma única variável de entrada para controlar uma única variável de saída. Esse tipo de controle é amplamente estudado e aplicado, especialmente em processos industriais que envolvem respostas simples e previsíveis, como aquecimento e controle de pressão em processos unitários (OGATA, 2010; SEBORG et al., 2011).
Com a evolução da automação e o aumento da complexidade dos processos industriais, surgiu a necessidade de arquiteturas de controle mais avançadas (ASTROM & MURRAY, 2008), como MISO (Multiple Input, Single Output), MIMO (Multiple Input, Multiple Output) e TITO (Two Input, Two Output). Essas configurações permitem controlar múltiplas variáveis simultaneamente, algo essencial em sistemas interdependentes, como reações químicas multicomponentes ou sistemas de produção de energia. A estrutura MISO, por exemplo, envolve várias entradas controlando uma única saída e é comumente utilizada em processos onde várias variáveis influenciam um único parâmetro de interesse. Embora aumente a flexibilidade, esse tipo de sistema apresenta desafios para a sintonia de controladores devido à interferência entre as entradas (SKOGESTAD & POSTLETHWAITE, 2005).
3 METODOLOGIA
O objetivo deste estudo foi aplicar e analisar a identificação do sistema por meio da regressão de Ridge, empregar a metodologia clássica de sintonia de um controlador PI pelo método do Controle por Modelo Interno e avaliar seu desempenho em uma planta de controle multivariável de temperatura e velocidade. A pesquisa é caracterizada como um estudo de caso, de caráter explicativo e abordagem qualitativa, com um desenho transversal no que se refere à dimensão temporal.
O instrumento de pesquisa foi estruturado conforme as etapas a seguir: observação do comportamento da planta de controle, tratamento dos dados iniciais, identificação do sistema, simulação do sistema de controle sintonizado de maneira conservadora e com uma ação mais rápida, seguida de uma análise do comportamento do sistema sintonizado com base nos critérios de desempenho. Cada uma dessas etapas será detalhada nos subtópicos a seguir.
3.1 Planta de Controle
A planta de controle foi projetada com duas malhas distintas: uma responsável pelo aquecimento e outra pelo resfriamento do sistema. O aquecimento do sistema é realizado por um resistor cerâmico de cimento, com capacidade de dissipação de 5 W, resistência de 4,7 Ω e precisão de ±5%. Esse elemento resistivo foi acoplado a um dissipador metálico de alumínio, com núcleo de cobre em contato direto com o resistor, utilizando pasta térmica para maximizar a condutividade térmica no ponto de contato.
O controle da temperatura é gerido por um sistema baseado no microcontrolador Arduino UNO R3, que faz uso de dois sensores: um sensor de temperatura, responsável pelo monitoramento térmico do resistor, e um sensor infravermelho, utilizado para medir a velocidade da ventoinha que atua no resfriamento do sistema. Esse cooler, por sua vez, melhora a troca de calor com o ambiente, permitindo um controle mais preciso da temperatura da planta.
Figura 1 – Componentes e sua disposição na montagem do sistema de controle.

A unidade de controle utilizada no estudo foi projetada para simulações e sintonia de um sistema de controle térmico, composta por diversos componentes eletrônicos que interagem de forma coordenada. A medição da temperatura foi realizada com um termistor do tipo NTC (Negative Temperature Coefficient), que apresenta resistência inversamente proporcional à temperatura. Este tipo de sensor é amplamente utilizado por sua alta sensibilidade e precisão na detecção de variações térmicas (FETEIRA, 2009).
O sistema controlado é responsivo aos sinais de modulação por largura de pulso (PWM) enviados por um microcontrolador, permitindo o controle da potência fornecida ao resistor cerâmico e a velocidade do cooler. O microcontrolador, por sua vez, é responsável por ler e registrar os dados fornecidos pelos sensores, utilizando um programa desenvolvido em C++.
A velocidade da ventoinha foi medida por um sensor infravermelho TCRT5000, utilizado no modo de detecção de objetos. Esse sensor, que funciona com base no circuito integrado LM393, compara o sinal refletido pelo LED infravermelho com um nível de tensão de referência. Quando um objeto (neste caso, o ventilador) altera a reflexão do sinal, o sensor gera um sinal digital, indicando a detecção da rotação do cooler (VISHAY, 2009).
Para resfriamento da planta, utilizou-se um cooler, que inclui um dissipador de calor, responsável por dispersar o calor gerado pela malha de aquecimento, e um ventilador que aumenta a eficiência do processo de resfriamento. O ventilador foi fixado em uma base de fenolite, garantindo estabilidade ao conjunto.
O controle do motor do cooler é realizado por meio de um driver de ponte H, baseado no chip L298N, que permite a modulação da potência fornecida ao ventilador através de sinais PWM. O driver controla o ciclo de trabalho (“duty cycle”), ajustando a quantidade de energia entregue ao motor da ventoinha (STMICROELECTRONICS, 2000). Por fim, a figura 02 mostra a planta de controle em sua totalidade.
Figura 2 – Planta de controle.

3.2 Observação do comportamento da Planta
Para observar a dinâmica do processo, foram realizadas duas simulações assistidas na planta, variando diferentes valores de entrada. Na primeira simulação, o cooler recebeu um sinal PWM zerado, porém, mesmo sem a modulação do sinal, a ventoinha operou em sua velocidade mínima de rotação. O processo de aquecimento foi assistido ao longo de 120 minutos, com variação das entradas de aquecimento a cada 12 minutos, utilizando 10 sinais de entrada distintos. Durante o experimento, o microcontrolador registrou os valores das variáveis de entrada e saída a cada 100 milissegundos.
De forma análoga, a segunda simulação teve como objetivo observar a dinâmica da malha de resfriamento. Nessa simulação, o sinal de entrada da malha de aquecimento foi mantido zerado, enquanto o sistema de resfriamento recebeu diferentes sinais de entrada, com intervalos de tempo iguais aos utilizados na primeira simulação. É valido lembrar, que no processo de resfriamento é controlado a velocidade de rotação do cooler.
3.3 Identificação do Sistema
O processo de identificação do sistema foi realizado utilizando os dados registrados nas simulações, aplicando a técnica de regressão de Ridge. Para isso, foi desenvolvido um algoritmo em Python, utilizando a biblioteca “control”, que é amplamente reconhecida por sua funcionalidade no tratamento de sistemas de controle que permitiu que fossem obtidas duas equações matemáticas que descrevem o comportamento do sistema em função das variáveis manipuladas e dos sinais de saída.
Após a coleta de dados, as equações resultantes foram organizadas na forma de razão entre as variáveis de saída e de entrada do sistema, a fim de criar uma função de transferência no domínio do tempo discreto. Essa função foi então submetida ao processo de Transformada Z, o que permitiu a conversão para o domínio de Laplace, representando o comportamento do sistema em termos de variáveis contínuas. Essa conversão foi realizada utilizando a técnica do Segurador de Ordem Zero (Zero-Order Hold), que é comumente utilizada para converter sistemas discretos de volta para o domínio contínuo.
3.4 Sintonia do Controlador
A sintonia dos controladores será realizada com base nos valores obtidos a partir da função de transferência do sistema, utilizando o método de Controle por Modelo Interno para sistemas de primeira ordem sem atraso. Serão aplicadas duas abordagens distintas de sintonia: uma abordagem conservadora, em que o parâmetro “λ” será igual ao valor de “τ” (constante de tempo do sistema), e uma abordagem mais agressiva, na qual “λ” será definido como 0,5*τ.
Após a implementação dessas sintonias, será registrado o comportamento da planta para cada uma das abordagens. A performance do sistema será avaliada utilizando critérios de desempenho amplamente reconhecidos na literatura.
4 RESULTADOS E DISCUSSÕES
A seção de Resultados e Discussões tem como objetivo apresentar e analisar os principais achados obtidos durante as etapas de simulação e validação do modelo desenvolvido para a planta de controle multivariável de velocidade e temperatura. Ela foi subdividida em seções que descrevem o comportamento do sistema, a execução da modelagem do processo controlado, o funcionamento da planta sob diferentes sintonias e, por fim, uma discussão sobre os resultados obtidos.
4.1 Comportamento do sistema
Durante as simulações iniciais, foram identificados pontos fora do padrão esperado, conhecidos como “outliers”, que interferiram na identificação precisa do modelo matemático que descreve o comportamento da planta de controle. Para garantir maior confiabilidade dos resultados, torna-se imprescindível aplicar um pré-processamento aos dados, eliminando esses outliers e reduzindo ruídos por meio de técnicas de suavização, como a aplicação de filtros apropriados. Montgomery e Runger (2021) destacam que o tratamento cuidadoso dos dados é fundamental para aprimorar a precisão nas análises e obter modelos matemáticos ajustados, elevando a qualidade e a validade dos resultados finais. Esse processo de preparação dos dados contribui significativamente para a estabilidade e a consistência das simulações, facilitando a obtenção de uma representação mais realista da dinâmica do sistema.
Após o pré-processamento dos dados, os resultados finais foram ilustrados nas Figuras 3 e 4. Nessas representações, o eixo x mostra o tempo decorrido durante a simulação, enquanto o eixo y1 exibe a resposta do sistema monitorada ao longo do tempo. Já o eixo y2 corresponde ao sinal de entrada aplicado ao sistema, que influenciou o comportamento observado na saída. Essa estrutura facilita a análise dos dados, permitindo uma compreensão visual da dinâmica de resposta do sistema em função das variações nos sinais de entrada.
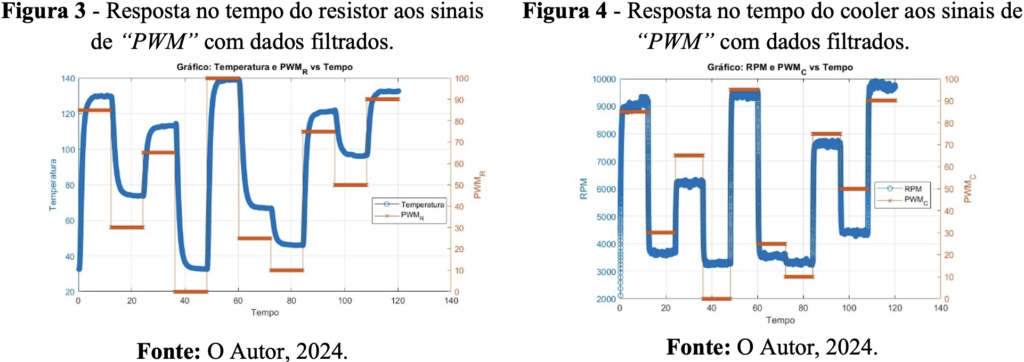
4.2 Modelagem Matemática da Planta.
Os dados, previamente tratados para remoção de outliers e suavizados com um filtro de dados, foram submetidos a um algoritmo de regressão de Ridge implementado em Python, utilizando a biblioteca “Control”. Esse procedimento resultou em uma equação no tempo discreto que descreve, de forma ajustada, o comportamento das malhas de controle do sistema. As Figuras 5 e 6 apresentam, respectivamente, as curvas ajustadas dos processos de aquecimento e resfriamento da planta. As Equações 4 e 5 mostram o resultado da regressão, expressando matematicamente o modelo estimado do sistema.
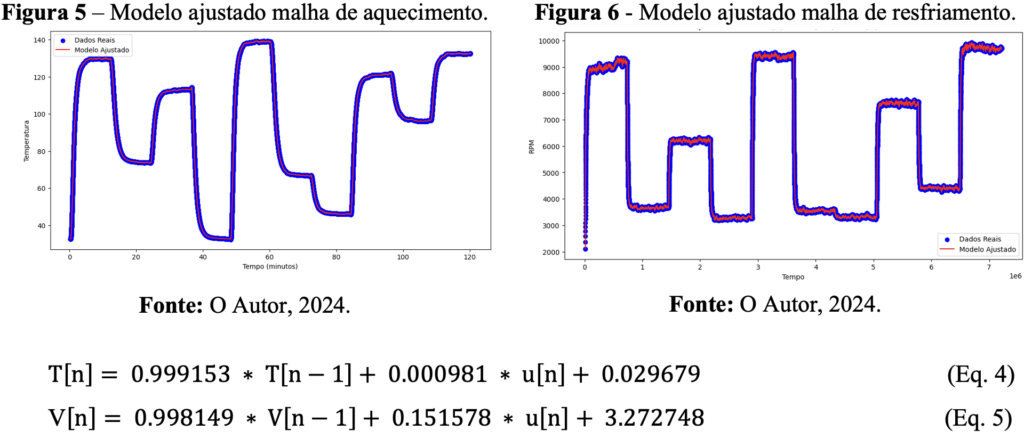
Por fim, após a aplicação das equações no tempo discreto, conforme descrito no item 2.2 do referencial teórico, foram obtidas as funções de transferência das duas malhas de controle. Esse processo foi realizado organizando os dados como uma razão entre saída e entrada, aplicando a transformada Z e, em seguida, convertendo para o domínio do tempo contínuo por meio do método do segurador de ordem zero. As expressões finais das funções de transferência estão apresentadas nas Equações 6 e 7, respectivamente, para a malha de aquecimento e para a malha de resfriamento.

4.3 Valores de sintonia.
Os parâmetros “Kp” e “Ti” foram determinados utilizando o método de Controle por Modelo Interno aplicado a uma função de primeira ordem sem atraso, conforme apresentado na Tabela 2. Os resultados foram obtidos para as duas malhas do sistema, com a aplicação de dois valores distintos para o parâmetro de ajuste “λ”: uma abordagem conservadora, que prioriza a estabilidade, e outra voltada para a otimização da velocidade de resposta. Os valores de “Kp” e “Ti” correspondentes a cada abordagem estão descritos na Tabela 3.
Tabela 3 – Valores de sintonia por IMC.
Kp Ti λ=Tau λ=(Tau/2) λ=Tau λ=(Tau/2) Malha de aquecimento 0,863271 1,726541 0,08473 0,08473 Malha de resfriamento 0,012213 0,024425 0,01853 0,018529
Fonte: Autor, 2024.
4.4 Funcionamento da planta sintonizada.
O estudo realizou a observação assistida do comportamento da planta de controle em duas abordagens de sintonia para um “setpoint” de 45°C, mantendo esse valor ao longo de 20 minutos. As Figuras 7 e 8 apresentam os resultados da resposta do sistema nas duas configurações de sintonia. Na Figura 7, observamos uma abordagem conservadora de sintonia, com um valor de lambda mais alto (λ=Tau).
Na Figura 8 é exibido a resposta da planta com o valor de lambda reduzido pela metade, o que produziu uma resposta mais rápida (λ=Tau/2).
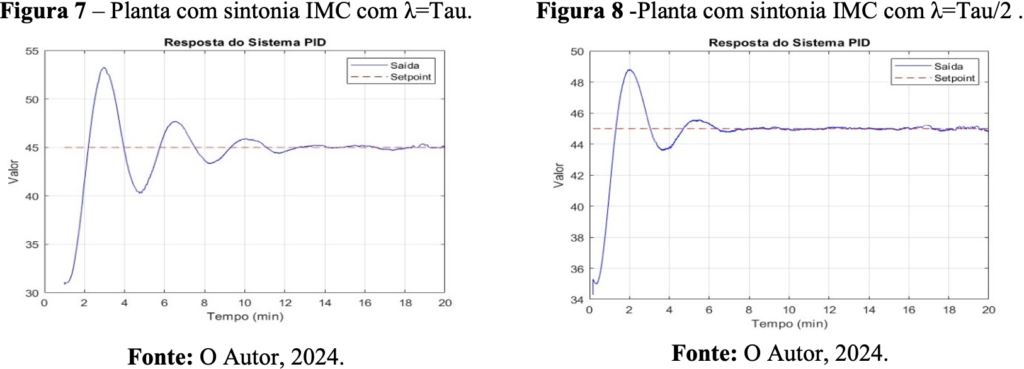
A análise da performance foi realizada por meio da observação do comportamento do sistema, utilizando os índices de critério de desempenho mencionados no tópico 2.4. Na Tabela 4, esses critérios foram organizados de forma a facilitar a análise e comparação dos resultados obtidos. Esse método de organização permite uma visão clara e objetiva dos dados, possibilitando uma avaliação precisa do sistema.
Tabela 4 – Índices de Desempenho.
Sintonia 1 (λ=Tau). Sintonia 2 (λ=Tau/2) Sobressinal máximo (Overshoot): 18,34% 8,48% Tempo do primeiro pico: 2.98 min 2,06 min Tempo de subida (10% a 90%): 0,95 min 0,80 min IAE : 32,62 14,45 ISE : 212,64 74,37 ITAE : 134,4 33,17 IPE (Índice de Performance Integral): 379,66 121,98
4.5 Discussões.
Os critérios de desempenho indicaram uma melhora significativa ao utilizar uma abordagem de sintonia mais agressiva com o método lambda, especialmente em comparação com o método conservador. Essa diferença se opõe aos conceitos apresentados por Garcia (2017), que descreve que uma configuração em que o valor de lambda é igual ao tempo tau tende a produzir respostas mais lentas, o que favorece a estabilidade ao minimizar variações na variável manipulada. Esta afirmação é indicada para processos monovariáveis.
As características físicas da planta de controle justificam os resultados observados. Sob uma sintonia conservadora, o sinal de controle varia em pequenos incrementos, levando a uma maior estabilidade. Quando a temperatura atinge o “setpoint”, o sinal de controle para a malha de aquecimento está elevado, enquanto o da malha de resfriamento permanece baixo. Essa configuração não proporciona uma resposta suficientemente rápida para compensar o efeito de memória térmica, resultando em um “overshoot” inicial. Em contrapartida, ao adotar uma sintonia mais agressiva (com um valor reduzido de lambda), observou-se uma diminuição de 9,48% no “overshoot” e uma redução de 257,68 pontos no índice de desempenho integral (IPE). Esses resultados reforçam a importância da escolha de parâmetros de sintonia conforme as características específicas da planta.
Como discutido por Campos e Teixeira (2019), as propriedades físicas de um sistema de controle são cruciais para a eficácia da sintonia, influenciando a resposta do sistema de controle de maneira substancial. Para sistemas dinâmicos com capacidade rápida de aquecimento e resfriamento, o método de controle IMC aplicado a uma função de transferência de primeira ordem sem atraso pode alcançar um desempenho satisfatório em regime permanente. Contudo, uma abordagem simplificada para processos multivariáveis não conseguiu explorar todo o potencial da planta, que possui capacidade de aquecimento e resfriamento muito mais rápida do que a resposta observada com essa estratégia.
5 CONSIDERAÇÕES FINAIS.
A presente pesquisa alcançou os objetivos propostos de modelagem matemática de uma planta multivariável de controle de temperatura e velocidade, utilizando a regressão de Ridge. Além disso, foi aplicada a sintonia pelo método de Controle do Modelo Interno para sistemas de primeira ordem sem atraso, inicialmente com uma abordagem conservadora, e posteriormente, com uma abordagem mais agressiva, variando o valor de “λ”. Observou-se que o método IMC, embora seja uma técnica de sintonia simplificada, permitiu obter uma estabilização aceitável do sistema em regime permanente. No entanto, não foi capaz de explorar totalmente o potencial da planta para uma estabilização rápida e com mínimo “overshoot” e abordagem conservadora para um processo multivariável não resultou em uma sintonia com menor erro devido as características intrínsecas do sistema de controle.
As perspectivas para pesquisas futuras incluem a aplicação de metodologias de sintonia mais robustas, como os métodos desenvolvidos por Åström e Hägglund, bem como aprimoramentos no algoritmo de controle PID para ajustar a intensidade das ações de controle de forma adaptativa. Em condições onde o sistema está distante do “setpoint”, incrementos maiores devem ser aplicados; enquanto em proximidade com o valor de referência, incrementos menores são preferíveis, maximizando a precisão e estabilidade do sistema. Essa abordagem pode ser complementada pelo método de Chien, Hrones e Reswick (1952), que permite uma sintonia com resposta rápida ou resposta lenta, dependendo do objetivo de controle, visando reduzir o “overshoot” e otimizar o desempenho.
REFERÊNCIAS
AGUIRRE, Luis Antonio. Introdução à Identificação de Sistemas: Técnicas Lineares e Não Lineares Aplicadas a Sistemas – Teoria e Aplicação. 4. ed. Belo Horizonte: UFMG, 2015. ISBN 978-8542300796.
ASTROM, K. J.; HAGGLUND, T. PID controllers: Theory, design and tuning. 2. ed. Research Triangle Park, USA: ISA, 1995.
ÅSTRÖM, Karl Johan; MURRAY, Richard M. Feedback Systems: An Introduction for Scientists and Engineers. Princeton: Princeton University Press, 2008. 408 p. ISBN 978-0691135762
ÅSTRÖM, Karl J.; WITTENMARK, Björn. Computer-controlled systems: theory and design. Courier Corporation, 2011. ISBN 978-0486486130.
CAMPOS, Mario Cesar M. Massa de; TEIXEIRA, Herbert C. G. Controles típicos de equipamentos e processos industriais. 2. ed. São Paulo: Blucher, 2010.
CHIEN, K. L.; HRONES, J. A.; RESWICK, J. B. On the Automatic Control of Generalized Passive Systems. Transactions of the American Society of Mechanical Engineers, v. 74, n. 2, p. 175-183, 1952.
DAHLIN, E. B. Designing and tuning digital controllers. Instruments & Control Systems, v. 41, n. 6, p. 77-83, 1968.
FETEIRA, Antonio. Negative Temperature Coefficient Resistance (NTCR) Ceramic Thermistors: An Industrial Perspective. Journal of the American Ceramic Society, v. 92, n. 5, p. 967–983, 2009. DOI: 10.1111/j.1551-2916.2009.02990.x.
GARCIA, Claudio. Controle de Processos Industriais: Estratégias Convencionais. Volume 1. 1. ed. São Paulo: Blucher, 2017. ISBN 978-8521211853.
HOERL, A. E.; KENNARD, R. W. Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics, v. 12, n. 1, p. 55-67, 1970.
LJUNG, L. System Identification: Theory for the User. 2. ed. New Jersey: Prentice Hall, 1999.
MONTGOMERY, Douglas C.; RUNGER, George C. Estatística Aplicada e Probabilidade para Engenheiros. 7. ed. Rio de Janeiro: LTC, 2021. ISBN 978-8521637332.
MORARI, M.; ZAFIRIOU, E. Robust Process Control. Englewood Cliffs, N.J.: Prentice Hall, 1989.
NISE, Norman S. Engenharia de Sistemas de Controle. 6. ed. Rio de Janeiro: LTC, 2012. ISBN 978-8521621355.
OGATA, Katsuhiko. Modern Control Engineering. 5. ed. Upper Saddle River: Prentice Hall, 2010. ISBN 978-8013616734.
SALEH, A. K. Md. Ehsanes; ARASHI, Mohammad; KIBRIA, B. M. Golam (Eds.). Theory of Ridge Regression Estimation with Applications. Hoboken: John Wiley & Sons, 2019. ISBN 9781118644478. DOI: 10.1002/9781118644478.
SKOGESTAD, S. Simple analytic rules for model reduction and PID controller tuning. Journal of Process Control, v. 13, n. 4, p. 291-309, 2003. SKOGESTAD, Sigurd; POSTLETHWAITE, Ian. Multivariable Feedback Control: Analysis and Design. 2. ed. Chichester: John Wiley & Sons, 2005. ISBN 978-0470011683.
¹Discente do Curso Superior de Bacharelado em Engenharia Elétrica do Instituto Centro Universitário Santo Agostinho – Anexo II. E-mail: eng.lucasamorimb@gmail.com
²Docente do Curso Superior de Bacharelado em Engenharia Elétrica do Instituto Centro Universitário Santo Agostinho. Mestre em Engenharia Elétrica pela Universidade Federal do Piauí (UFPI). E-mail: stenio.coelho@unifsa.com.br
