REGISTRO DOI: 10.69849/revistaft/ra10202411132102
Beatriz Felipe Guzeloto
Caio Victor Sepúlveda Rojas da Silva
Gabriela Maria Oliveira da Nóbrega
Marcella Toreta Frignani
Orientador: Bernardo Goisman
Resumo
O comércio eletrônico no Brasil continua a crescer e transformar os padrões de consumo, inclusive no setor de varejo de autopeças. Com isso, a previsão da demanda é importante para melhorar a gestão e controle de estoque. A assertividade leva a uma melhoria na experiência do cliente. Este artigo, a partir de dados de vendas de um e-commerce de autopeças do ABC paulista, visa desenvolver e comparar diferentes modelos de previsão de demanda para diversas categorias de produtos. O trabalho incluirá levantamento teórico, coleta de dados históricos, categorização por meio da curva ABC e utilização do software Crystal Ball®. As cinco estratégias de modelagem propostas permitem avaliar o desempenho da abordagem baseadas em séries temporais, contribuindo para melhoria da precisão nas previsões e, consequentemente, na eficiência operacional da empresa.
Palavras-chave: Previsão de demanda, Séries temporais, Crystal Ball®, Curva ABC, E-commerce.
Abstract
E-commerce in Brazil continues to grow and transform consumption patterns, including in the auto parts retail sector. Therefore, forecasting demand is important to improve inventory management and control. Assertiveness leads to an improvement in the customer experience. This article, based on sales data from an auto parts e-commerce in ABC São Paulo, aims to develop and compare different demand forecast models for different product categories. The work will include theoretical research, historical data collection, categorization using the ABC curve and use of Crystal Ball® software. The five proposed modeling strategies allow evaluating the performance of the approach based on time series, contributing to improving forecast accuracy and, consequently, the company’s operational efficiency.
Keywords: Demand forecasting, Time series, Crystal Ball®, ABC curve, E-commerce.
CAPÍTULO 1. INTRODUÇÃO
O contínuo crescimento do comércio eletrônico no Brasil tem transformado os padrões de consumo, forçando os gestores a enfrentar novos desafios operacionais e a explorar novas oportunidades emergentes no gerenciamento dessas atividades. Em 2023, a força desse mercado foi evidenciada por um faturamento de R$ 185 bilhões (ABCOMM, 2023a). Adicionalmente, no mesmo período, houve um total de 395 milhões de pedidos (ABCOMM,2023b). Esses números destacam a importância e a crescente influência do comércio eletrônico na economia brasileira.
Entre os setores que têm se beneficiado dessa expansão está o de autopeças, que atende a uma variedade de necessidades dos proprietários de veículos e profissionais da área de manutenção automotiva. De acordo com Delazeri (2023), a venda online de peças para carros combina urgência e conveniência. Em um cenário de alta competitividade, a capacidade de prever a demanda de produtos com precisão se torna um diferencial estratégico para garantir a disponibilidade dos itens, minimizar custos de estoque e melhorar a experiência do cliente.
No entanto, assim como ocorre em todos os setores de vendas, o e-commerce de autopeças enfrenta uma série de desafios e incertezas relacionados ao controle de estoque e atendimento da demanda. Segundo Viana (2002), os estoques são recursos ociosos que possuem valor econômico e representam um investimento destinado a incrementar as atividades de produção e atender aos clientes.
O planejamento é uma das atividades essenciais para um controle de estoque eficiente, englobando uma série de decisões relevantes que são parte integrante desse processo ou que dele derivam. Dentre essas decisões, destaca-se a previsão de demanda. A capacidade de prever a demanda é fundamental para a maioria dos processos operacionais, pois sem estimativas adequadas, torna-se inviável planejar o nível das atividades esperadas, além de dificultar o planejamento e a projeção dos recursos necessários para atender às demandas do mercado (LEWIS, 1997).
Neste contexto, o presente artigo realizará um estudo de caso em um e-commerce de autopeças, sediado no ABC paulista. Ela possui cerca de 50 funcionários e vende peças para suspensão, motores, direção, câmbio, transmissão, freios e componentes.
O objetivo geral deste trabalho consiste em criar, para cada categoria de produtos, diferentes modelos de previsão de demanda. Tais modelos serão comparados, segundo critério de erro, de forma a escolher o modelo mais adequado para previsão de cada categoria de produtos. Através da análise e teste desses modelos de previsão, pretende-se determinar qual deles oferece as previsões mais precisas e confiáveis para orientar as decisões estratégicas e operacionais da empresa em relação à gestão de estoque, produção e planejamento de vendas.
Para alcançar o objetivo geral deste trabalho, uma sequência de etapas será realizada. Inicialmente, será feito um levantamento de conteúdo teórico relevante para a resolução do problema em questão. Em seguida, serão coletados os dados históricos de vendas da empresa. Posteriormente, esses dados serão agrupados em diferentes categorias. Uma vez definidas as categorias, será utilizada a metodologia conhecida como curva ABC para definição de quais categorias pertencem, respectivamente, às classes A, B e C. A seguir, o software Crystal Ball®, será utilizado para desenvolver modelos de previsão de demanda para os produtos classe A, conforme uma métrica de erro pré-definida.
CAPÍTULO 2. REFERENCIAL TEÓRICO
2.1. Curva ABC
A Curva ABC, ou Classificação ABC, é uma ferramenta que auxilia os gestores das organizações a planejarem o estoque orientando os esforços em direção aos resultados significativos da empresa. Segundo Ribeiro (2022), o método é composto por três classificações, sendo elas:
Curva A: Itens de alta prioridade, os quais corresponderão a 80% do valor do estoque;
Curva B: Itens intermediários, os quais corresponderão a 15% do valor do estoque;
Curva C: Itens intermediários, os quais corresponderão a 5% do valor do estoque.
A metodologia da Curva ABC estabelece inicialmente três prioridades distintas, porém, sua aplicação pode ser estendida para incluir um número maior de prioridades, de acordo com as exigências de cada ambiente organizacional. Os valores padrão pré-definidos, geralmente 80%, 15% e 5%, embora utilizados na maioria dos casos, são subjetivos e podem variar conforme as estratégias específicas de cada empresa (BALLOU,2006). A figura 1 exemplifica os dados ao serem plotados num gráfico formando a curva ABC:
Figura 1 – Exemplo de uma Curva ABC
Fonte: CCa Express (2019)
Através da análise e da representação gráfica da Curva ABC, é possível identificar os itens que requerem atenção e tratamento adequado. Alguns itens possuem grande quantidade física, mas baixa importância financeira, por serem de pequeno valor dentro do estoque. Em contrapartida, outros itens, embora em menor quantidade física, possuem alta importância financeira, devido ao seu grande valor no conjunto do estoque (PONTES, 2013).
A técnica representa uma abordagem estratégica para categorizar e priorizar de itens com base em critérios específicos, como quantidade estocada, valor financeiro retido e espaço físico ocupado, oferecendo uma visão abrangente da distribuição dos recursos, permitindo uma tomada de decisão mais precisa dentro do contexto organizacional (SLACK et al.,2010).
O método é uma ferramenta empregada para aprimorar a gestão de estoques, proporcionando benefícios como a obtenção de informações confiáveis para decisões futuras de reposição (KNABBEN et al., 2019).
Para Santa Ana (2021), informações sobre as oscilações do estoque no tempo podem ser utilizadas para prever demandas futuras. Considerando o objetivo geral, a curva ABC auxilia na identificação dos itens que requerem atenção especial do gestor.
2.2. Previsão de demanda
Segundo Dias (2015), a previsão de demanda consiste em um estudo detalhado que visa obter informações precisas sobre as vendas futuras de produtos e/ou serviços em um determinado mercado.
As empresas, muitas vezes, não podem aguardar a chegada dos pedidos para iniciar a determinação qualitativa e quantitativa dos equipamentos de produção necessários. Adicionalmente, os insumos devem ser negociados antecipadamente com os fornecedores. Isso implica que o fabricante deve prever a demanda por seu produto e, assim, assegurar a capacidade de produção e as respectivas matérias primas. Esta atividade exige a projeção das vendas de um determinado produto, convertendo essa projeção na demanda correspondente pelos elementos de produção e providenciando sua aquisição (MAYER, 1990).
Dada a competitividade do ambiente empresarial, Fernandes e Godinho (2010) destacam a importância de analisar as demandas futuras, já que elas fornecem dados essenciais para diversas funções e decisões no Planejamento e Controle da Produção (PCP), como a orientação para o planejamento estratégico de produção, vendas e finanças. Dessa maneira, a previsão de demandas fundamenta a formulação de políticas de estoque, a alocação adequada de recursos financeiros, a eliminação e substituição de produtos não rentáveis, o desenvolvimento de controles eficientes, entre outros aspectos (RUSSOMANO, 2000).
O lead time é importante para previsão e planejamento. Este é definido como o intervalo entre a percepção de um evento e sua materialização. O propósito da previsão é antecipar ações, e sua relevância para a organização está diretamente ligada à capacidade de gerar ações tangíveis e efetivas (MAKRIDAKIS et al., 1998).
Na elaboração de previsões, é importante a distinção de eventos externos incontroláveis, como aqueles provenientes da economia, governo e concorrência, e eventos internos controláveis, como estratégias de marketing e decisões de produção internas à empresa (MAKRIDAKIS et al., 1998).
Os métodos de previsão de demanda podem ser classificados em dois grandes grupos: qualitativos e quantitativos. Os quantitativos, por sua vez, se desdobram em métodos causais e séries temporais. Esses grupos apresentam diferenças em termos de precisão e acurácia de acordo com o horizonte de previsão, nível de sofisticação do modelo e base de dados necessária (BALLOU, 2006).
2.2.1. Métodos Qualitativos
A escolha de como será feita a previsão da demanda depende muito da natureza dos dados à disposição. Ao ter dificuldade em encontrar informações e/ou em não havendo dados quantitativos para fazê-la, a abordagem mais indicada é a qualitativa (LAGE JÚNIOR, 2019).
Os métodos qualitativos são fundamentados em considerações de especialistas que, por conhecimento e experiência, podem analisar e emitir opiniões sobre tendências futuras de relevância. Contudo, essas não se restringem apenas às previsões de demanda, podendo ser utilizadas em movimentos do comércio internacional, tendências de novos produtos, futuras condições econômicas e políticas, etc. (MOREIRA, 2012).
Dentro dessa abordagem, é possível encontrar diferentes métodos. Podem ser citados, entre outros: método Delphi, análise da força de venda e pesquisa de mercado.
2.2.1.1. Método Delphi
Iniciado em 1948 pela RAND Corporation para avaliar o impacto de um possível ataque nuclear aos Estados Unidos, o método Delphi se expandiu para diversas áreas, especialmente na previsão de mudanças tecnológicas e seus impactos nas organizações. É usado principalmente em situações de longo prazo, onde os dados são limitados ou inexistentes, e o julgamento pessoal torna-se importante (MOREIRA, 2012).
O método envolve a consulta a um grupo de especialistas para obter suas opiniões sobre um determinado assunto, seguindo regras específicas para coletá-las e processá-las. Então, o grupo é formado e cada membro expressa seu ponto de vista de forma independente, geralmente por meio de questionários. As respostas são então resumidas e redistribuídas ao grupo, destacando as opiniões divergentes. Os participantes são convidados a revisar suas teses com base nas novas informações recebidas. Este ciclo é repetido várias vezes até que se alcance um consenso (MOREIRA, 2012).
Entre as vantagens do método Delphi está a possibilidade de coletar ideias individuais sem a influência direta entre os participantes, o que pode evitar distorções. Contudo, o método depende da qualidade dos questionários utilizados e não oferece um meio para discutir ambiguidades diretamente, o que pode limitar sua eficácia em certos contextos (MOREIRA, 2012).
2.2.1.2. Análise de força de venda
A análise da força de vendas é importante para prever vendas futuras, ajustando-as conforme tendências e mudanças de mercado. Empresas com armazéns regionais, por exemplo, dependem dessas previsões para planejar a distribuição adequada de produtos (GUERRINI et al., 2019).
Embora contar com a equipe de vendas para essas previsões seja benéfico, existem riscos. Vendedores podem confundir intenções de compra com ações efetivas dos clientes, podem ser influenciados por eventos recentes e a imposição de cotas de vendas ou comissões é capaz de influir em seus julgamentos. Portanto, é essencial equilibrar as opiniões da equipe de vendas com uma análise objetiva para garantir previsões confiáveis (MOREIRA, 2012).
2.2.1.3. Pesquisa de mercado
Entender a demanda do mercado envolve ouvir os consumidores, pois são eles que a definem. Quando se lida com um grupo de consumidores potencialmente grande, torna-se inviável consultar cada um individualmente. Por isso, opta-se pela amostragem, realizando o que é conhecido como pesquisa de mercado. Este tipo de pesquisa exige conhecimento especializado e cuidado detalhado desde o planejamento até a interpretação dos dados coletados. A realização bem-sucedida de uma pesquisa de mercado, que requer profissionais qualificados e recursos adequados, pode trazer insights valiosos para a empresa (MOREIRA, 2012).
2.2.2. Métodos Quantitativos
Os métodos quantitativos são técnicas científicas para coletar e analisar dados, modelar e interpretar os modelos. Devido a sua capacidade de transformar dados em informações mensuráveis para tomada de decisões, eles são amplamente utilizados em diversas áreas como Economia, Finanças, Administração, Medicina, Biologia entre outras. Pode-se definir métodos quantitativos como o uso de técnicas, modelos matemáticos e/ou formas de análise de dados e informações para resolução ou investigação de problemas tornando dados antes não organizados em objetos mensuráveis, permitindo a melhor compreensão para encontro de resultados. Para Moreira (2012, p. 294) “métodos quantitativos são aqueles que utilizam modelos matemáticos para se chegar aos valores previstos. Permitem controle do erro, mas exigem informações quantitativas preliminares”.
Para Siqueira (2013, p.3) “os métodos quantitativos aplicados são uma combinação das ciências matemáticas, estatísticas e computacionais”.
Portanto as técnicas disponíveis para uso em estudos podem ser adaptadas ou mesmo podem ser mais bem indicadas para levantamento de soluções à medida que as ciências avançam. “Os problemas das organizações evoluem em quantidade, em complexidade e em competências. Os métodos quantitativos aplicados também evoluem no mesmo sentido” (SIQUEIRA, 2013, p.8).
No caso em estudo, os modelos quantitativos para previsão de demanda são os métodos causais e as séries temporais.
2.2.2.1. Métodos Causais
Os métodos causais são técnicas que utilizam a relação entre a demanda de um produto ou serviço e variáveis que podem influenciar na previsão delas. Esse método considera fatores externos que são capazes de impactar significativamente futuras demandas. Ao dizer a respeito dos métodos causais, Moreira faz as seguintes considerações:
A demanda de um item ou conjunto de itens é relacionada a uma ou mais variáveis internas ou externas à empresa. Essas variáveis são chamadas de variáveis causais. A população, o PNB (Produto Nacional Bruto), o número de alvarás expedidos para construção, o consumo de certos produtos etc. são alguns exemplos de variáveis causais. Na verdade, o que determina a escolha de uma particular variável causal para a previsão da demanda é a sua ligação lógica com essa última. Se tivermos uma boa estimativa desse valor, ser possível obter a projeção desejada para um produto ou grupo de produtos em estudo (MOREIRA, P.294, 2012).
Para Lage Júnior (2019), a utilização dessa abordagem necessita de algum fator causal que influencie os dados de maneira conhecida e que auxiliarão na previsão. Dentro dessa perspectiva, existem diversos métodos. Entre eles, pode-se mencionar: regressão linear, regressão polinomial e regressão múltipla.
A título de exemplo, será explicado a regressão simples. Segundo Moreira (2012), esta técnica é utilizada para modelar a relação entre uma variável dependente e uma variável independente, com o objetivo de ajustar uma curva que melhor represente essa relação. A eq. (1) mostra uma relação na regressão simples:

“Nesta, Y é chamada de variável dependente e X é a variável independente. O símbolo f(X) indica que os valores de Y podem ser determinados caso sejam conhecidos os valores de Y. Portanto Y é uma função de Y” (MOREIRA 2012, p. 298).
Quando se faz uso de regressão simples, tem-se várias alternativas para o formato da função Y=f(x)
A figura 2 retrata a representação gráfica da regressão linear simples:
Figura 2 – Representação gráfica da regressão linear simples
Fonte: Dev.to (2020)
2.2.2.2. Séries Temporais
As séries temporais são importantes na análise de dados ao longo do tempo, representando uma sequência de observações de uma variável em intervalos regulares, como dias ou meses. Essas observações permitem estimativas de valores futuros baseadas em tendências passadas. O uso dessas séries é amplamente aceito devido à sua base lógica e aplicabilidade prática em previsões (MOREIRA, 2012).
Existem dois grupos de aplicações de séries temporais: previsão e classificação. Na previsão, o objetivo é identificar padrões que permitam prever valores futuros, como tendências do dólar ou vendas de produtos. A classificação envolve a identificação de padrões em momentos específicos, como a diferenciação entre batimentos cardíacos normais e anormais em um eletrocardiograma (SPADINI, 2021).
Para Santos et al (2020), um modelo que utiliza séries temporais depende exclusivamente de dados históricos de, por exemplo, demanda. As previsões baseadas nesse modelo utilizam a premissa de que os valores do futuro são projeções dos valores do passado, sem sofrer qualquer influência de outras variáveis. Para construí-lo, é necessário mapear os dados históricos e analisar os fatores que são capazes de alterar as características da curva obtida (TUBINO, 2017).
Características essas que se originam de quatro componentes: tendência, sazonalidade, ciclo e aleatoriedade (GUERRINI et al., 2019). A tendência representa a direção-geral dos dados ao longo do tempo, seja ela crescente ou decrescente. A sazonalidade reflete padrões repetitivos ou flutuações que ocorrem em intervalos regulares. Os ciclos são variações que ocorrem devido a mudanças econômicas ou outras influências, enquanto a aleatoriedade é a variação que não pode ser explicada por outros elementos (MOREIRA, 2012).
As séries temporais podem ser classificadas como univariadas ou multivariadas. As univariadas envolvem uma única variável sendo analisada ao longo do tempo. Em contraste, as multivariadas envolvem diferentes variáveis inter-relacionadas (SOUZA, 1981).
Na análise de séries temporais, diversas abordagens são adotadas para atender as diferentes necessidades de modelagem dos dados. São algumas das opções de métodos dessa abordagem: média móvel simples, média móvel ponderada, suavização exponencial simples, suavização exponencial dupla (ou método de Holt) e suavização exponencial tripla (ou método de Winters). Cada um desses métodos é selecionado com base na estrutura dos dados e no tipo de previsão desejada, permitindo uma modelagem mais precisa e eficaz (LAGE JÚNIOR, 2019).
2.2.2.2.1. Média Móvel Simples (MMS)
Segundo Tubino (2017), a média móvel simples é calculada com base nos dados mais recentes, substituindo o dado mais antigo pelo mais novo a cada novo período. Corrêa e Corrêa (2022) ressaltam a importância de escolher o período correto para a média, seja ele de três, seis ou mais meses, dependendo do objetivo da sua vização. A eq. (2) mostra o cálculo da MMS:

No mercado de ações, por exemplo, a média móvel simples é aplicada para facilitar a identificação de tendências (JACOBS; CHASE, 2009).
Lage Júnior (2019) ressalta que, ao utilizar os dados mais recentes, a média móvel simples responde rapidamente a mudanças, tornando-a ideal para processos estáveis. No entanto, Moreira (2012) adverte que, embora a média móvel simples possa ser eficiente para demandas estacionárias, ela pode não ser adequada para captar tendências de longo prazo ou variações sazonais, o que é uma consideração importante ao aplicar essa técnica em qualquer análise preditiva.
2.2.2.2.2. Média Móvel Ponderada (MMP)
Ao contrário da média móvel simples, a média móvel ponderada (MMP) não atribui o mesmo peso a todos os dados (LAUGENI; MARTINS, 2015). Jacob e Chase (2009) destacam que, enquanto a MMS considera todos os períodos igualmente, a MMP permite a atribuição de pesos variáveis, que quando somados devem ser iguais à 1, tendo flexibilidade para enfatizar informações mais relevantes, como os dados mais recentes.
Ainda para Jacobs e Chase (2009), a escolha dos pesos na MMP é muito importante e pode ser baseada, por exemplo, em experiência ou tentativa e erro. Para Moreira (2012) e Tubino (2017), normalmente, dá-se maior peso aos dados recentes, refletindo sua maior relevância para prever tendências futuras. A eq. (3) mostra o cálculo geral para a MMP:

Apesar de suas vantagens, a MMP tem ressalvas. Segundo Jacobs e Chase (2009), ela pode ser mais custosa do que métodos como a média ponderada exponencial. A escolha arbitrária de (n) e dos pesos pode afetar a precisão das previsões, e é essencial considerar o equilíbrio entre a resposta a variações na demanda (MOREIRA. 2012).
2.2.2.2.3. Suavização Exponencial Simples
A suavização exponencial surgiu no final da década de 1950, proposta por pioneiros como Brown, Holt e Winters. Esta técnica revolucionou os métodos de previsão ao introduzir médias ponderadas que atribuem pesos decrescentes a observações mais antigas. Sua aplicabilidade e eficácia rapidamente a tornaram uma ferramenta valiosa para análises de séries temporais em diversos setores industriais (HYNDMAN; ATHANASOPOULOS, 2021).
O método de suavização exponencial simples calcula previsões utilizando uma fórmula que considera a demanda real do último período e a previsão anterior, ajustadas por uma constante de suavização, α. Esta constante, variando entre 0 e 1, determina o peso dado às observações recentes em contraste com as mais antigas, refletindo a relevância temporal dos dados na modelagem de previsões (JACOBS; CHASE, 2009). A eq. (4) mostra o cálculo do método:

O valor de α é importante no ajuste do modelo de suavização exponencial. Um α maior prioriza informações recentes, tornando o modelo mais responsivo a mudanças recentes, enquanto um α menor dá mais importância ao histórico de dados, proporcionando uma previsão mais estável e menos suscetível a variações pontuais (LAGE JÚNIOR, 2019).
2.2.2.2.4. Método de Holt (Suavização Exponencial Dupla)
O método de suavização exponencial dupla, conhecido como método Holt, foi desenvolvido por Holt, em 1957. De acordo com Makridakis et al. (1998), o modelo de Holt pode ser utilizado, de maneira satisfatória, em séries temporais com tendências lineares bem definidas. Este método oferece refinamentos adicionais na modelagem, à medida que introduz uma constante de suavização que afeta a tendência da série. Sua diferença para o modelo simples está na utilização de duas constantes de suavização, α e β, que são encontradas por interações a fim de buscar o menor erro médio quadrático, por exemplo. Os seus valores sempre irão variar entre 0 e 1. As equações (5) e (6) são responsáveis pela estimativa de nível e inclinação da série temporal, já a (7) calcula a previsão de demanda nos próximos n períodos.

Para lidar com a subjetividade na escolha dos parâmetros e , são propostos métodos para a seleção desses parâmetros de forma a otimizar várias métricas de desempenho de previsões, como o erro médio (ME), erro absoluto médio (MAE) e erro quadrático médio (MSE) (BILLAH et al., 2010). Por outro lado, Rasmussen (2004) sugere uma abordagem para calcular tanto os parâmetros e que aprimoram o método de previsão quanto os valores iniciais, utilizando o MSE como função objetivo para minimizar.
2.2.2.2.5. Método de Holt-Winters (Suavização Exponencial Tripla)
O modelo Holt-Winters estende o trabalho de Holt ao incluir uma componente sazonal, permitindo que ele lide com séries temporais que exibem tanto tendências quanto padrões sazonais. Essa extensão faz com que o algoritmo seja altamente eficaz em capturar e prever esses comportamentos cíclicos em dados temporais (TEBALDI, 2019).
O método Holt-Winters decompõe a série temporal em três componentes: nível, que representa o valor médio da série em um determinado ponto no tempo; tendência, componente que indica a direção e a magnitude da mudança na série ao longo do tempo e por fim, a sazonalidade, capturando os padrões cíclicos que ocorrem em intervalos regulares (MORETTIN; TOLOI, 2006).
Os modelos exponenciais se dividem entre: aditivo e multiplicativo.
Quando a amplitude da sazonalidade é constante, a variante aditiva é utilizada e suas fórmulas são:

2.2.2.2.6. Modelo ARIMA
De acordo com Ediger e Akar (2007), o modelo autorregressivo integrado de médias móveis, conhecido como ARIMA, é amplamente utilizado para prever a demanda em séries temporais devido à sua capacidade de modelar dados que exibem comportamentos não-estacionários. O modelo ARIMA é particularmente útil para séries que apresentam tendências e variações complexas ao longo do tempo. Ao lidar com essas séries, o modelo aplica diferenciações para estabilizar as propriedades estatísticas, tornando os dados estacionários antes de realizar a modelagem e a previsão (MORETTIN; TOLOI, 2006).

Como destacado por Werner e Ribeiro (2003), o componente autorregressivo (p) quantifica a relação entre valores consecutivos da série, enquanto a integração verifica a estacionariedade da série, aplicando diferenciações (d) para estabilizar os dados. A média móvel (q) considera o impacto das variações mais recentes, suavizando a série para refletir uma tendência mais clara, facilitando assim a interpretação e a previsão das séries temporais complexas.
2.3. Medidas de Erros
Tratar diferentes tipos de informações permite a realização de estudos que envolvem uma cadeia de decisões que podem ser tomadas para diversas áreas, desde os campos sociais, exatas e até mesmo os biológicos. Com base nos dados disponíveis é possível supor diferentes modelos sobre os temas em questão. Quando se pensa em modelos, é possível inferir diversos destes para prever o que pode acontecer. Pode-se pensar que o conjunto de informações disponíveis, num determinado tempo, pode ser base para determinar o que pode acontecer no futuro. O conjunto de dados observados num determinado período é usado em séries temporais (SOUSA et al. 2021). Para Bowersox, Cooper e Closs (2006), a precisão da previsão envolve diferença entre as previsões e as vendas reais correspondentes. Avaliação e análise de erros são necessárias para aperfeiçoar a precisão da previsão.
Para realizar previsões em qualquer contexto, é crucial entender e avaliar a precisão das previsões. Neste caso, as medidas de erro desempenham um papel fundamental nesse processo, pois permitem uma análise imparcial de quão próximas às previsões estão dos valores reais. Essas medidas podem ser utilizadas para tomada de decisão em áreas, tais como demanda de produtos nos variados setores, demanda de serviços nas mais diversas áreas. Para se avaliar a precisão das previsões, é necessário medir e analisar os erros que se apresentam. É possível mensurar e acompanhar a amplitude dos erros de previsão de várias formas, contudo, o erro médio absoluto e o erro médio quadrático são os mais usuais (CORRÊA; CORRÊA, 2006).
Para Hyndman e Koehler (2006), as medidas absolutas são dependentes da escala, o que significa que dependem da ordem de grandeza dos dados em estudo. Para este tipo, as medidas mais comuns são: Erro Absoluto Médio (Median Absolute Deviation – MAD), Erro Quadrático Médio (Mean Square Error – MSE) e Raiz do Erro Quadrático Médio (Root Mean Square Error – RMSE). Adicionalmente, há medidas relativas de erro; nesta se enquadra o Erro Absoluto Percentual Médio (Mean Absolute Percentage Error – MAPE).
2.3.1. Erro MAD
O desvio médio absoluto (MAD) é determinado pela análise das discrepâncias entre as previsões de demanda e os valores reais observados. Trata-se de medida absoluta de erro (SILVA et al.,2022).
O seu principal objetivo é avaliar a variabilidade de erros. Quanto menor for o valor do MAD, mais próximo à realidade estarão as previsões (TUBINO, 2017). A eq. (16) mostra o cálculo do modelo:

2.3.2. Erro MAPE
O erro absoluto percentual médio (MAPE) mede, em módulo, a percentagem média dos erros da previsão. Quanto menor esse valor, mais precisa será a previsão. Trata-se de medida relativa de erro (OLIVEIRA JÚNIOR, 2021).
Um ponto negativo do MAPE é onde há valores observados iguais à zero, o MAPE se aproximará a valores infinitos (MIRANDA, 2014).
Para calcular o MAPE usa-se a eq. (17):

2.3.3. Erro MSE
O erro quadrático médio (MSE) é dado pela média dos quadrados dos erros. Quanto mais discrepantes forem os dados da previsão em relação ao valor real, maior será seu valor. Por outro lado, quanto mais próximo à previsão estiver do valor real, menor ele será (MIRANDA, 2014).
O MSE é um modelo popularmente usado devido a sua fácil compreensão e cálculo. Tem como característica principal a sua sensibilidade a grandes erros (TAVARES, 2020).

2.3.4. Erro RMSE
O root mean squared error (RMSE) – raíz do erro quadrático médio, é muito parecido com o erro MSE, porém com um acréscimo de uma raiz na fórmula. O RMSE adiciona a raiz quadrada à fórmula do MSE para transformar as unidades de medida dos erros de quadradas para lineares, tornando-os diretamente comparáveis com os valores originais (OLIVEIRA JÚNIOR, 2021).
Um modelo que minimiza o RMSE tende a ter previsões que se aproximam da média dos dados (HYNDMAN; ATHANASOPOULOS, 2021). A sua fórmula é dada pela eq. (19):
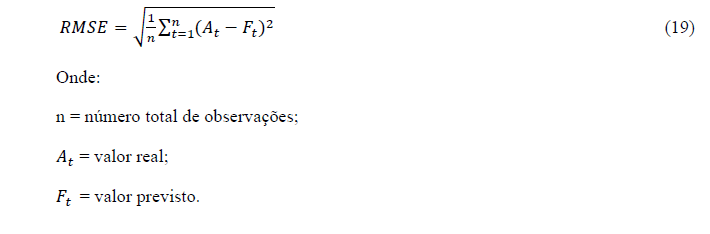
2.4. U de Theil
O coeficiente U de Theil, criado pelo econometrista holandês Henri Theil, é uma métrica que avalia a precisão das previsões. Quanto mais próximo de zero for o valor do coeficiente, menor é o erro de previsão do modelo em comparação com uma previsão simples ou ingênua. Em outras palavras, indica que o modelo fornece uma previsão superior à trivial (MAKRIDAKIS et al., 1998).
Essa métrica de precisão é capaz de medir o quão bem um modelo de previsão se comporta comparando-o com uma previsão simples. A eq. (20) mostra como é calculado:

De acordo com Makridakis et al. (1998), uma das vantagens do coeficiente U de Theil é a capacidade de realizar comparações relativas. Ele permite uma comparação direta entre a performance do modelo e uma previsão ingênua, oferecendo uma referência prática para avaliar a eficiência relativa dos modelos preditivos.
2.5. Crystal Ball
O Oracle Crystal Ball® é um software de simulação, análise preditiva e otimização para realizar as modelagens das previsões. É utilizado em diversas áreas, como finanças, engenharia e gestão de projetos para analisar dados descritos em planilhas do Microsoft Excel. Ele proporciona uma compreensão profunda dos elementos críticos, capacitando o usuário a tomar decisões táticas e precisas para alcançar metas e garantir uma vantagem competitiva, mesmo em cenários de incerteza (Oracle, 2020).
2.5.1. Funcionamento do Crystal Ball®
Primeiramente, o Crystal Ball® é integrado ao Microsoft Excel, tornando-se disponível no menu como uma nova guia. Quando essa guia é selecionada, a faixa de opções correspondente é exibida, como ilustrado na Figura 3.

O acesso ao “Predictor” é feito na seleção do respectivo ícone mostrado na figura 3.
O processo de previsão no software começa com a entrada de dados históricos na tela “Inserir Dados” no campo “Local de série de dados” conforme ilustra a figura 4. Esses dados são importados de uma planilha Excel contendo, por exemplo, informações de vendas dos produtos para os períodos sucessivos analisados. É importante selecionar a opção “Dados em linhas” conforme os dados estejam dispostos em linhas.
Os dados também podem estar dispostos em colunas. Neste caso, a opção adequada seria “Dados em colunas”.
Figura 4 – Tela “Inserir Dados” do Crystal Ball®
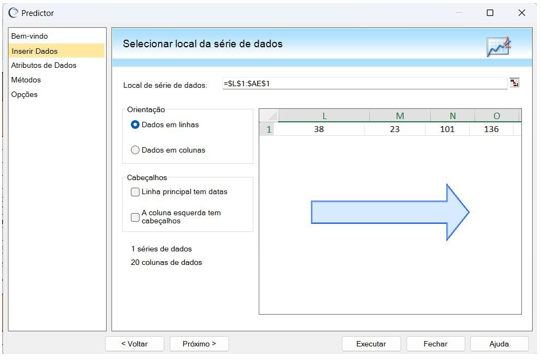
Fonte: Autoria própria (2024)
Selecionado o item “Próximo”, aparece a seção “Atributos de dados”.
Na seção “Atributos de Dados” apresentada na figura 5, é onde é possível configurar as características dos dados que serão utilizados para realizar a previsão. Nessa tela é definido o intervalo de datas, isto é, sua unidade. As variáveis a serem analisadas são escolhidas e filtros ou transformações podem ser aplicados caso seja necessário. Isso é importante para garantir que o software entenda os dados corretamente e possa fazer previsões precisas.
Figura 5 – Tela “Atributos de Dados” do Crystal Ball®
Fonte: Autoria própria (2024)
Novamente seleciona-se o item “Próximo”, aparecendo a seção “Métodos”.
Conforme é mostrado na figura 6, a tela “Métodos” permite escolher os modelos estatísticos candidatos a fazer a previsão. Nela é possível selecionar entre diferentes opções, como: ARIMA, Regressão Linear Múltipla, Métodos Sazonais e Não Sazonais.
Figura 6 – Tela “Métodos” do Crystal Ball®
Fonte: Autoria própria (2024)
Selecionado novamente o item “Próximo”, aparece a seção “Opções”.
Segundo a figura 7, na tela “Opções”, o software permite que as configurações adicionais sejam ajustadas para a previsão. No campo de “Medida de erro” foi selecionada, no exemplo, a opção MAPE, pois ajuda a avaliar a precisão das previsões em termos percentuais. Há, adicionalmente, as técnicas MAD e RMSE para medidas de erro.
Já no campo de “Técnica de previsão” foi selecionado “Previsão Padrão”, pois define a técnica básica para a geração das previsões, garantindo uma abordagem inicial e confiável para análise.
Figura 7 – Tela “Opções” do Crystal Ball®
Fonte: Autoria própria (2024)
Uma vez configurado o software, seleciona-se a opção “Executar”.
Nos “Resultados do Predictor” é exibida uma análise detalhada das previsões geradas pelo modelo selecionado. No exemplo usado, é possível identificar diversas informações. A figura 8 mostra, no canto superior direito, entre outras informações, que foram utilizados 20 pontos de dados no total, com valor mínimo de 23,00, média igual a 502,00 e valor máximo de 934,00, mostrando a amplitude dos dados. O desvio padrão de 289,53 indica a dispersão dos dados em torno da média.
O MAPE de 29,02% revela a precisão da previsão em termos percentuais, o U de Theil de 0,8289 sugere um resultado superior se comparado a um modelo de previsão “ingênuo” simples, e o valor de Durbin-Watson de 2,14 indica que não há correlação significativa nos erros da previsão. Esses resultados mostram que o modelo selecionado para esta previsão foi o Média Móvel Dupla. Este modelo possui menor MAPE. Foram feitas previsões para 2 períodos, conforme o canto inferior direito da figura 8. A figura 9 mostra, em tabela, os dados usados e os valores obtidos para o exemplo. A figura 9 é obtida ao selecionar o tópico “Exibir” e escolher-se o item “Tabela”.
Figura 8 – Exibição do Gráfico na Tela de Resultados do Predictor no Crystal Ball®
Fonte: Autoria própria (2024)
Figura 9 – Exibição da Tabela na Tela de Resultados do Predictor no Crystal Ball®
Fonte: Autoria própria (2024)
CAPÍTULO 3. METODOLOGIA
Para a empresa definida, serão coletados dados de venda de todos os produtos no período de setembro de 2022 até julho de 2024.
O portfólio é composto de 529 produtos agrupados em 45 categorias.
Tais categorias serão organizadas e ordenadas segundo uma curva ABC de vendas com vendas acumuladas de setembro de 2022 até abril de 2024.
Serão selecionadas as categorias classificadas como “A” na curva ABC as categorias ordenadas cuja soma acumulada de vendas chegue até 80% do volume total.
Para fazer a previsão de cada categoria para os meses de maio, junho e julho, o Crystal Ball® será usado através de 5 estratégias distintas:
• O Crystal Ball® será executado com todos os dados do período;
• Será feita uma análise prévia dos dados. Em princípio, será gerada uma regressão linear e serão comparados os dados reais com os dados da regressão. Os dados cujos erros percentuais forem maiores serão retirados da entrada de dados. Nestes casos, os dados retirados serão substituídos por um campo vazio. O software, então, completará os campos vazios usando uma estratégia pré-definida no sistema. Serão substituídos, pelo Crystal Ball®, 10% do total de dados;
• Será feita uma análise prévia dos dados. Em princípio será gerada uma regressão linear e serão comparados os dados reais com os dados da regressão. Os dados cujos erros absolutos forem maiores serão retirados da entrada de dados. Nestes casos, os dados retirados serão substituídos por um campo vazio. O software, então, completará os campos vazios usando uma estratégia pré-definida no sistema. Serão substituídos, pelo Crystal Ball®, 10% do total de dados;
• Será feita uma análise prévia dos dados. Em princípio será gerada uma regressão linear e serão comparados os dados reais com os dados da regressão. Os dados cujos erros percentuais forem maiores serão retirados da entrada de dados. Nestes casos, os dados retirados serão substituídos pelos respectivos dados da regressão. Serão substituídos, pelo grupo, 10% do total de dados;
• Será feita uma análise prévia dos dados. Em princípio será gerada uma regressão linear e serão comparados os dados reais com os dados da regressão. Os dados cujos erros absolutos forem maiores serão retirados da entrada de dados. Nestes casos, os dados retirados serão substituídos pelos respectivos dados da regressão. Serão substituídos, pelo grupo, 10% do total de dados.
Adicionalmente, para fazer a previsão de cada categoria, o Crystal Ball® será usado através de 5 estratégias distintas a partir da métrica de erro MAPE.
Uma vez executado o Crystal Ball®, para cada produto com métrica de erros MAPE, será mostrada uma tabela contendo mês a mês e uma tabela contendo a média do acumulado.
Será levantado um roteiro de perguntas com a finalidade de fazer as análises de forma comparativa entre os dados. Sendo elas:
1) A partir do erro acumulado MAPE, identificar qual a categoria menos previsível e a mais previsível para os meses em que foram feitas as previsões.
2) Qual a estratégia mais adequada para prever as vendas para cada categoria para os meses em que foram feitas as previsões?
Para responder as perguntas 1 e 2, deverá ser preenchida a tabela 1 e, posteriormente, a tabela 2.
Tabela 1 – MAPE do modelo em cada período
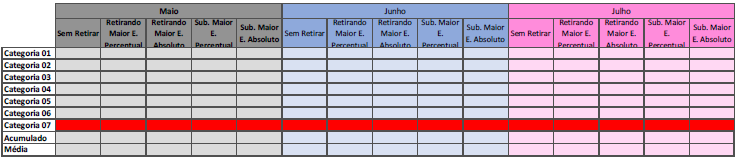
Fonte: Autoria própria (2024)
Tabela 2 – Média do acumulado por categoria
Fonte: Autoria própria (2024)
3) Definir a melhor estratégia e modelo para cada produto.
Para responder à pergunta 3, deverá ser usada a tabela 2.
4) Como se comporta, cada categoria, em cada estratégia, quando se comparado o MAPE passado com o MAPE medido no futuro?
Para responder à pergunta 4, deverá ser preenchida a tabela 3 e, posteriormente, a tabela 4.
Tabela 3 – Comparação MAPES real X histórico
Fonte: Autoria própria (2024)
A tabela 4 representa a distância, o módulo, entre o erro absoluto do MAPE real e o MAPE histórico, para cada uma das estratégias de cada categoria.
Tabela 4 – Erro absoluto entre MAPE real x histórico
Fonte: Autoria própria (2024)
5) Quantas vezes a manipulação dos dados com heurísticas vence o modelo de método padrão?
A tabela 5 mostra o “Sem Retirar” contra a heurística em que o maior erro percentual é retirado, posteriormente será feito a mesma comparação entre o “Sem Retirar” e as outras heurísticas.
Tabela 5 – Sem Retirar X Retirando maior erro percentual
Fonte: Autoria própria (2024)
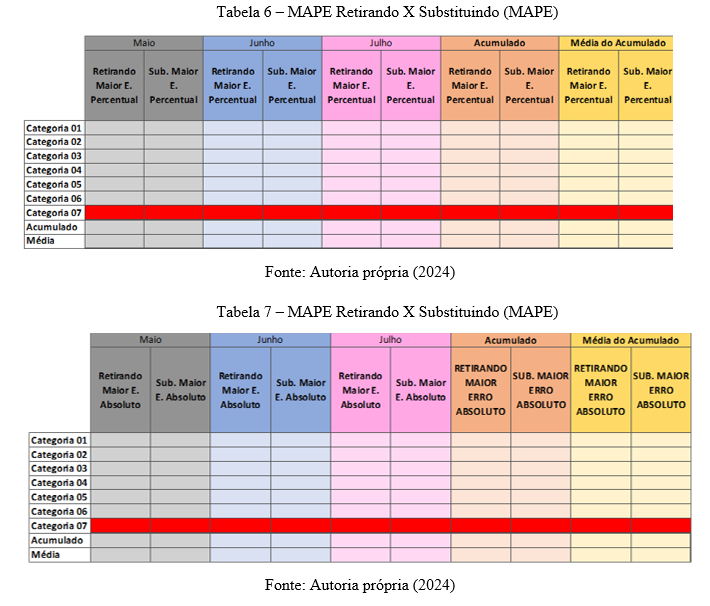
6) Dentre as heurísticas analisadas, supondo que teremos que retirar os dados, quem é mais preciso, técnicas de substituição manual ou as executadas via software? Serão avaliados casos de substituição e retirada baseados em erros absolutos e erros percentuais.
As tabelas 6 e 7 deverão ser preenchidas.
7) Quais os modelos de previsão aparecem com mais frequência para cada categoria?
8) Quais os modelos de previsão aparecem com maior frequência no total das categorias em função do número de “aparições”?
Para responder as perguntas 7 e 8, deverá ser preenchida a tabela 8.
Tabela 8 – Frequência dos modelos
Fonte: Autoria própria (2024)
CAPÍTULO 4: RESULTADOS E DISCUSSÕES
4.1. Descrição da empresa
Fundada em março de 1984, e situada no ABC Paulista, conta com uma equipe de aproximadamente 50 funcionários. Opera no mercado de varejo de autopeças e oferece uma ampla gama de peças para suspensão, motores, direção, câmbio, transmissão, freios e componentes em geral.
A empresa, hoje, opera em duas frentes: o e-commerce para vendas em geral e uma loja física que oferece serviços como troca de óleo, retífica de freio (tambor e disco) e limpeza de bico. O presente artigo concentrará seu estudo de caso nas vendas realizadas através da plataforma de e-commerce.
4.2. Coleta de dados e aplicação da Curva ABC
Através da coleta de dados das vendas, realizada entre setembro de 2022 e abril de 2024, foi identificado que a empresa possui 529 produtos em seu catálogo, que somam 28.810 itens vendidos. Para facilitar a análise, esses produtos foram agrupados por categoria. O passo subsequente foi classificar essas categorias conforme sua importância, em vendas totais, para a empresa.
A figura 10 apresenta a classificação ABC, onde a quantidade que representa até 80% das vendas é classificada como A, os 15% seguintes são B e o restante corresponde a C.
Figura 10 – Classificação ABC dos produtos
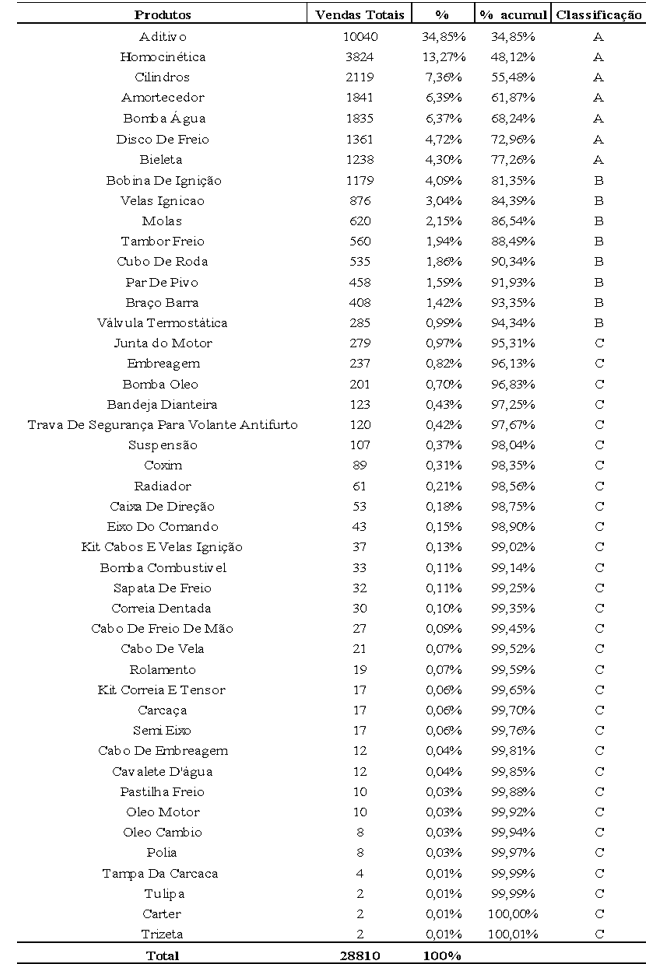
Fonte: Autoria própria (2024)
A análise dos dados apresentados na figura 11 mostra que a empresa deve concentrar uma atenção especial em 15,56% de suas categorias de produtos, pois essas representam 77,26% do total de vendas. Essas categorias foram selecionadas como foco principal para o presente estudo devido à sua significativa contribuição para o desempenho comercial da empresa.
Figura 11 – Proporções por classe
Fonte: Autoria própria (2024)
O gráfico 1 mostra a curva ABC da classificação, a partir da segmentação de classificação dos dados coletados:
Gráfico 1 – Curva ABC
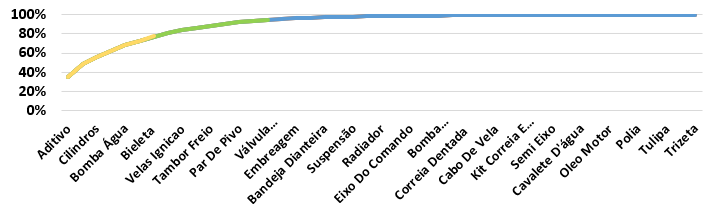
Fonte: Autoria própria (2024)
4.2.3. Análise dos dados coletados
Com base nos dados coletados e na análise realizada, as recomendações das tabelas preenchidas são específicas para este caso e não se aplicam a outras situações. Vale ressaltar que a categoria 07, apesar de ter sido classificada como A na curva ABC, não contém dados suficientes para que sejam feitas análises e previsões de forma precisa.
Seguindo a metodologia proposta serão respondidas as 8 perguntas pré-estabelecidas:
1) A partir do erro acumulado MAPE, identificar qual a categoria menos previsível e a mais previsível para os meses em que foram feitas as previsões.
A tabela 9 fornece uma visão do desempenho mensal para cada produto de forma a compreender a assertividade de cinco estratégias distintas, sendo elas: “Sem Retirar”, “Retirando Maior Erro Percentual”, “Retirando Maior Erro Absoluto”, “Substituindo Maior Erro Percentual” e “Substituindo Maior Erro Absoluto”.
Tabela 9 – MAPE do modelo em cada período
Fonte: Autoria própria (2024)
Com base nos dados obtidos pela tabela 9, é possível extrair informações que darão origem à tabela 10.
A partir da tabela 10 é possível determinar qual categoria é a menos previsível, a mais previsível e a estratégia mais adequada para prever as vendas.
A premissa para se responder à pergunta é verificar, em cada categoria, qual a melhor estratégia de previsão. A melhor estratégia de previsão de categoria é aquela em que se incorre no menor erro.
Tabela 10 – Média do acumulado por categoria
Fonte: Autoria própria (2024)
Com base na tabela 10, tem-se:
a) A categoria em que há maior assertividade é 06 e a estratégia adotada foi “Substituir o maior erro percentual”. O erro MAPE encontrado foi de 3,85%.
b) A categoria em que há menor assertividade é 01 e a estratégia adotada foi “Substituir o maior erro percentual”. O erro MAPE encontrado foi 16,42%.
A categoria 01 se mostra menos previsível. Nela há diversos aditivos. Tais produtos geram volume de vendas na plataforma comercializada, isto é, são vendidos por um preço, normalmente, abaixo do mercado.
2) Qual a estratégia mais adequada para prever as vendas para cada categoria para os meses em que foram feitas as previsões?
É possível identificar, com base nos dados analisados na tabela 10, que as estratégias mais adequadas para cada categoria são:
Categoria 01: Substituindo Maior Erro Percentual;
Categoria 02: Substituindo Maior Erro Absoluto;
Categoria 03: Substituindo Maior Erro Absoluto;
Categoria 04: Retirando Maior Erro Percentual;
Categoria 05: Substituindo Maior Erro Absoluto e Substituindo Maior Erro Percentual;
Categoria 06: Substituindo Maior Erro Percentual.
3) Definir a melhor estratégia e modelo para cada produto.
A partir da resposta da pergunta número 2, onde foi definido a melhor estratégia para cada categoria, o software forneceu os respectivos modelos:
Categoria 01: ARIMA (1.1.0); Substituição do Maior Erro Percentual;
Categoria 02: Suavização exponencial dupla; Substituição do Maior Erro Absoluto;
Categoria 03: Suavização exponencial dupla; Substituição do Maior Erro Absoluto;
Categoria 04: Suavização exponencial dupla; Retirando Maior Erro Percentual;
Categoria 05: Média móvel simples; Substituição do Maior Erro Percentual e/ou Substituição do Maior Erro Absoluto;
Categoria 06: Média móvel dupla; Substituição do Maior Erro Percentual.
4) Como se comporta, cada categoria, em cada estratégia, quando se comparado o MAPE passado com o MAPE medido no futuro?
A tabela 11 fornece a média dos módulos do MAPE dos dados do passado e do futuro, sendo os dados do futuro representados pela média do acumulado.
Utiliza-se, como base de análise, a média de cada estratégia de cada categoria. O intuito é comparar a disparidade entre o passado e o futuro, utilizando os MAPES reais e os MAPES históricos.
Tabela 11 – Comparação MAPES real X histórico
Fonte: Autoria própria (2024)
A tabela 12 representa distância, o módulo, entre o erro absoluto do MAPE real e o MAPE histórico, para cada uma das estratégias de cada categoria.
Tabela 12 – Erro Absoluto: Passado X Futuro
Fonte: Autoria própria (2024)
Pode-se concluir que as distâncias não ultrapassam 20%. Não houve, regra geral, oscilações superiores a tal valor.
5) Quantas vezes a manipulação dos dados com heurísticas vence o modelo de método padrão?
Serão comparadas cada uma das quatro estratégias em que houve intervenção no Crystal Ball com a estratégia “Sem retirar”.
A tabela 13 mostra, nas 2 últimas colunas, os erros MAPE entre as estratégias “Sem Retirar” e “Retirando maior erro percentual”.
Tabela 13 – Sem Retirar X Retirando maior erro percentual
Fonte: Autoria própria (2024)
Com base no acumulado e na média do acumulado da tabela 13, é possível identificar que em quatro das seis categorias válidas, o “Sem Retirar” perde para a heurística “Retirando Maior Erro Percentual”.
A tabela 14 mostra, nas 2 últimas colunas, os erros MAPE entre as estratégias “Sem Retirar” e “Retirando maior erro absoluto”.
Tabela 14 – Sem Retirar X Retirando maior erro absoluto
Fonte: Autoria própria (2024)
Com isso, é possível identificar que em quatro das seis categorias válidas, o “Sem Retirar” perde para a heurística “Retirando Maior Erro Absoluto”.
A tabela 15 mostra, nas 2 últimas colunas, os erros MAPE entre as estratégias “Sem Retirar” e “Substituindo maior erro percentual”.
Tabela 15 – Sem Retirar X Substituindo maior erro percentual
Fonte: Autoria própria (2024)
Sendo possível identificar que em todas as categorias válidas, o “Sem Retirar” perde para a heurística “Substituindo Maior Erro Percentual”.
Por fim, a tabela 16 mostra, nas 2 últimas coluna os erros MAPE entre as estratégias “Sem Retirar” e “Substituindo Maior Erro Absoluto”
Tabela 16 – Sem Retirar X Substituindo maior erro absoluto
Fonte: Autoria própria (2024)
Portanto, é possível identificar que em cinco das seis categorias válidas, o “Sem Retirar” perde para a heurística “Substituindo Maior Erro Absoluto”.
No geral, o “Sem Retirar” quando comparado a qualquer outra heurística tem resultados inferiores, ou seja, o percentual de erro dele é maior na maioria dos casos. Portanto, o uso de uma heurística acaba sendo mais assertivo. Porém, vale ressaltar que as conclusões e sugestões elaboradas foram desenvolvidas com base nas particularidades e nas condições específicas deste cenário.
6) Dentre as heurísticas analisadas, supondo que teremos que retirar os dados, quem é mais preciso, técnicas de substituição manual ou as executadas via software?
Assumindo que os dados de maior erro percentual serão retirados, sendo no máximo 10% dos dados, as heurísticas contidas na tabela 17 serão comparadas entre si, a fim de determinar quem é mais assertiva, onde:
• Retirando Maior Erro Percentual: O software completará os campos vazios usando uma estratégia pré-definida no sistema.
• Substituindo Maior Erro Percentual: Os dados retirados serão substituídos pelos respectivos dados da regressão.
Tabela 17 – MAPE Retirando X Substituindo (MAPE)
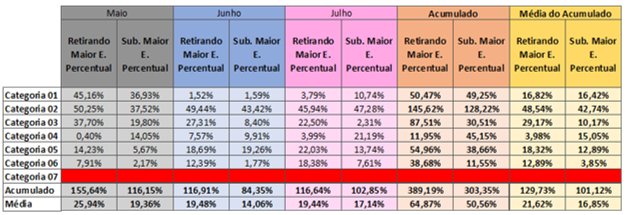
Fonte: Autoria própria (2024)
Assim, a heurística “Substituindo Maior Erro Percentual” se sobressai em cinco das seis categorias válidas, ou seja, substituir os dados pela regressão mostrou-se mais eficiente em relação ao software.
Neste contexto, as heurísticas contidas na tabela 18 também serão comparadas entre si:
• Retirando Maior Erro Absoluto: O software completará os campos vazios usando uma estratégia pré-definida no sistema.
• Substituindo Maior Erro Absoluto: Os dados retirados serão substituídos pelos respectivos dados da regressão.
Tabela 18 – MAPE Retirando X Substituindo (MAPE)
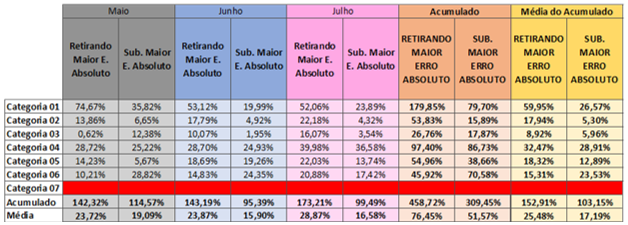
Fonte: Autoria própria (2024)
É possível notar que o mesmo comportamento se repete na tabela 18. Sendo a heurística “Substituindo Maior Erro Absoluto” mais assertiva em relação ao software.
As questões 7, e 8, “Quais os modelos de previsão aparecem com mais frequência para cada categoria?” e “Quais os modelos de previsão aparecem com maior frequência no total das categorias em função do número de “aparições”?” serão respondidas conjuntamente.
Para responder tais perguntas, utiliza-se a tabela 19, que mostra a frequência de recomendações de modelos gerados pelo software nas diferentes simulações, para cada categoria.
Considera-se que “Nº de Aparições nas Categorias” representa a incidência dos modelos nas categorias, e não a soma de suas aparições.
Tabela 19 – Frequência dos modelos
Fonte: Autoria própria (2024)
De acordo com a tabela 19, pode-se afirmar que para as categorias 01, 04 e 06, o modelo que mais aparece é a Média Móvel Dupla, totalizando o maior número de recomendações feitas pelo software quando comparado com os demais modelos em suas categorias. Isto indica que os dados para estas categorias apresentam tendência. Já na categoria 02, o modelo que mais aparece é a Tendência Amortecida Não Sazonal, evidenciando que os dados para esta categoria têm tendência, porém não há sazonalidade. Para a categorias 03, pode-se observar que a predominância feita pelo software é para a Suavização Exponencial Dupla.
Por fim, na categoria 05 nota-se um empate entre os modelos Média Móvel Simples e SARIMA (1.0.0) (0.0.1). Os dois modelos sugeridos são distintos, pois enquanto um não apresenta sazonalidade nem tendência, o outro exibe ambas as particularidades. Fato esse, que se dá pela manipulação dos dados aplicada nas heurísticas.
Em resumo, pode-se denotar que os modelos de previsão que mais se repetem dentre as categorias, são: Média Móvel Simples, Média Móvel Dupla e Suavização Exponencial Dupla.
CAPÍTULO 5. CONSIDERAÇÕES FINAIS
As séries temporais possuem limitações pois não estabelecem, diretamente, uma causalidade entre as vendas e as variáveis determinantes das vendas. Por outro lado, possuem mais chance de aplicabilidade pois exigem somente uma série histórica utilizada para criação de modelos.
Métodos quantitativos via séries temporais, no estudo de caso, se mostraram adequados para previsões.
Para cada categoria, houve 5 estratégias distintas usadas para criação de modelos de previsão com séries temporais.
A primeira estratégia consistiu no uso de tabela com série temporal para obtenção de modelo de previsão.
As duas estratégias seguintes consistiram na retirada de dados da tabela com série temporal. A escolha dos pontos a serem retirados levavam em conta erro percentual e erro absoluto. Uma vez retirados os pontos, a ferramenta completava tais pontos faltantes.
As duas últimas estratégias consistiram na retirada de dados da tabela com série temporal e posterior substituição por pontos obtidos via modelos de regressão. A escolha dos pontos a serem retirados levavam em conta erro percentual e erro absoluto. A substituição não foi feita pela ferramenta e sim via modelos de regressão.
O que se notou foi uma melhora na assertividade das quatro últimas estratégias, quando comparadas à primeira estratégia.
Sugere-se, entre outras possibilidades, como trabalho futuro, o uso de modelos causais para previsão de demanda.
REFERÊNCIAS
ABCOMM. Associação Brasileira de Comércio. Números do E-commerce. Disponível em: <https://dados.abcomm.org>. Acesso em: 20 mai. 2024a.
ABCOMM. Associação Brasileira de Comércio Eletrônico. Evolução do E-commerce. Disponível em: <https://dados.abcomm.org/crescimento-do-ecommerce-brasileiro>. Acesso em: 20 mai. 2024b.
BALLOU, R H., Gerenciamento da Cadeia de Suprimentos/Logística Empresarial. 5. ed. Porto Alegre: Bookman, 2006.
BILLAH, B.; KING, M. L.; SNYDER, R. D.; KOEHLER, A. B. Exponential smoothing model selection for forecasting. International Journal of Forecasting, v. 22, n. 2, p. 239-247, jun. 2006. DOI https://doi.org/10.1016/j.ijforecast.2005.08.002. Disponível em: <https://www.sciencedirect.com/science/article/abs/pii/S016920700500107X?via%3Dihub>. Acesso em: 18 mai. 2024.
BOWERSOX, D. J.; COOPER, M. B.; CLOSS, D. J. Gestão logística de cadeias de suprimentos. 1. ed. Porto Alegre: Bookman, 2006. 528 p.
CCAEXPRESS. Disponível em <http://www.ccaexpress.com.br/blog/curva-abc-para-estoque-e-vendas-como-fazer/>. Acesso em: 23 mai. 2024.
CORRÊA, H. L.; CORRÊA, C. A. Administração de produção e operações: manufatura e serviços: uma abordagem estratégica. 2. ed. São Paulo: Atlas, 2006.
CORRÊA, H. L.; CORRÊA, C. A. Administração de produção e operações: manufatura e serviços: uma abordagem estratégica. 5. ed. Barueri, SP: Atlas, 2022.
DELAZERI, J. Estratégias poderosas para impulsionar o e-commerce de autopeças. ABComm, 2023. Disponível em: <https://abcomm.org/noticias/estrategias-poderosas-para-impulsionar-o-e-commerce-de-autopecas/>. Acesso em: 20 mai. 2024.
DIAS, M. A. Administração de materiais: uma abordagem logística. São Paulo: Atlas, 2015.
EDIGER, V. Ş.; AKAR, S. ARIMA forecasting of primary energy demand by fuel in Turkey. Energy Policy, v. 35, n. 3, p. 1701-1708, mar. 2007. DOI https://doi.org/10.1016/j.enpol.2006.05.009. Disponível em: <https://www.sciencedirect.com/science/article/abs/pii/S0301421506002291>. Acesso em: 27 abr. 2024
FERNANDES, F. C. F.; GODINHO, F. M. Planejamento e controle da produção: dos fundamentos ao essencial. São Paulo: Atlas, 2010.
GUERRINI, F. M.; BELHOT, R. V.; JÚNIOR, W. A. Planejamento e controle da produção: modelagem e implementação. 2. ed. Rio de Janeiro: Elaevier, 2019.
HYNDMAN, R. J.; ATHANASOPOULOS, G. Forecasting: principles and practice. 3. ed. Melbourne, Austrália: OTexts, 2021. Disponível em: <OTexts.com/fpp3>. Acesso em: 25 abr. 2024.
HYNDMAN, R. J.; KOEHLER, A. B. Another look at measures of forecast accuracy. International Journal of Forecasting. v. 22. n. 4, p. 679-688, out.-dez. 2006. DOI https://doi.org/10.1016/j.ijforecast.2006.03.001. Disponível em: <https://www.sciencedirect.com/science/article/abs/pii/S0169207006000239>. Acesso em: 30 mai. 2024.
JACOBS, F. R.; CHASE, R. B. Administração da produção e de operações: o essencial. Porto Alegre: Bookman, 2009.
LAGE JÚNIOR, M. Planejamento e controle da produção: teoria e prática. 1. ed. Rio de Janeiro: LTC, 2019.
KNABBEN J. A.; WERNKE, R.; RUFFATO, I.; JUNGES, I. Comparação entre o custo financeiro da estocagem e a curva ABC: estudo de caso em indústria de autopeças. Revista Produção Industrial & Serviços, v. 6, n. 1, p. 1–12, dez. 2019.
LAUGENI, F. P.; MARTINS, P. G. Administração da produção. 3. ed. São Paulo: Saraiva, 2015.
LEWIS, C. D. Demand Forecasting and Inventory Control. New York: Wiley, 1997.
MAKRIDAKIS, S.; WHEELWRIGHT, S. C.; HYNDMAN, R. J. Forecasting: methods and applications. 3. ed. New York: John Wiley, 1998.
MAYER, R. R. Administração da Produção. São Paulo: Atlas, 1990.
MIRANDA, I. P. H. Comparação de diferentes métodos de previsão em séries temporais com valores discrepantes. 2014. Trabalho de Conclusão de Curso (Bacharelado em Estatística) – Instituto de Ciências Exatas, Universidade Federal de Juiz de Fora, Juiz de Fora, 2014.
MOREIRA, D. A. Administração da Produção e Operações. 2. ed. Revista e ampliada, São Paulo: Cengage Learning, 2012.
MORETTIN, P. A.; TOLOI, C. Análise de Séries Temporais. São Paulo: Edgar Blucher, 2006.
OLIVEIRA JÚNIOR, C. Métricas para Regressão: entendendo as métricas R², MAE, MAPE, MSE e RMSE. Medium: Data Hackers, dez. 2021. Disponível em: <https://medium.com/data-hackers/prevendo-n%C3%BAmeros-entendendo-m%C3%A9tricas-de-regress%C3%A3o-35545e011e70>. Acesso em: 30 mai. 2024.
ORACLE. Crystal Ball. Disponível em: https://www.oracle.com/br/applications/crystalball/. Acesso em: 27 de jul. de 2024
PONTES, A. E. L. Gestão de estoques: utilização das ferramentas curva ABC e classificação XYZ em uma farmácia hospitalar. 2013. Trabalho de Conclusão de Curso (Graduação em Farmácia) – Universidade Federal da Paraíba, João Pessoa, 2013. Disponível em: <https://repositorio.ufpb.br/jspui/handle/123456789/551>. Acesso em: 17 mai. 2024.
RASMUSSEN, R. On time series data and optimal parameters. Omega, v. 32, n. 2, p. 111-120, abr. 2004. DOI https://doi.org/10.1016/j.omega.2003.09.013. Disponível em: <https://www.sciencedirect.com/science/article/abs/pii/S0305048303001130?via%3Dihub>. Acesso em: 13 abr. 2024.
RIBEIRO, L. O. M. Ferramentas qualitativas e quantitativas aplicadas à tomada de decisão em logística. 1. ed. Rio de Janeiro: Freitas Bastos, 2022. E-book. Disponível em: <https://plataforma.bvirtual.com.br>. Acesso em: 17 mai. 2024.
RUSSOMANO, V. H. Planejamento e controle da produção. São Paulo: Pioneira, 2000.
SANTA ANA, M. D. F. A Curva ABC na Gestão de Estoque. Brazilian Journal of Development, Curitiba, v. 7, n. 5, p. 53737-53749, mai. 2021. Disponível em: <https://ojs.brazilianjournals.com.br/ojs/index.php/BRJD/article/view/30580/24032>. Acesso em: 17 maio 2024.
SANTOS, A. F. et al. Planejamento e controle de produção. Porto Alegre: SAGAH, 2020.
SILVA, T. C. et al. Análises de modelos de previsão de demanda para uma empresa do setor automobilístico. In: ENCONTRO NACIONAL DE ENGENHARIA DE PRODUÇÃO, XLII., 2022, Foz do Iguaçu, Paraná. Anais […]. Enegep [S. l.: s. n.], 2022.
SIQUEIRA, J. O. Fundamentos de Métodos Quantitativos: aplicados em administração, economia e contabilidade atuária. São Paulo: SRV Editora LTDA, 2013. E-book. ISBN 9788502125872. Disponível em: <https://integrada.minhabiblioteca.com.br/#/books/9788502125872/>. Acesso em: 18 maio 2024.
SLACK, N.; CHAMBERS, S.; JOHNSTON, R. Administração da Produção. São Paulo: Atlas, 2002.
SOUZA, A.R.S. et al. Análise de séries temporais. Porto Alegre: SAGAH, 2021.
SOUZA, R. C. Metodologias para a análise e previsão de séries temporais univariadas e multivariadas. Brazilian Review of Econometrics, v. 1, n. 2, p. 78-92. São Paulo, nov. 1981. DOI https://doi.org/10.12660/bre.v1n21981.3167. Disponível em: https://periodicos.fgv.br/bre/article/view/3167/2062>. Acesso em: 30 mai. 2024.
SOUZA, T. F. de; GUIMARÃES, T. A. Escolha e utilização de um modelo de previsão de demanda em serviços: estudo de caso em uma empresa prestadora de serviços de recapagem de pneus. In: ENCONTRO NACIONAL DE ENGENHARIA DE PRODUÇÃO, 30., 2010, São Carlos. Anais […]. Enegep [S. l.: s. n.], 2010.
SPADINI, A. S. Séries temporais e suas aplicações. Alura, 22 jan. 2021. Disponível em: <https://www.alura.com.br/artigos/series-temporais-e-suas-aplicacoes>. Acesso em: 3 junho 2024.
TAVARES, M. A. A. Previsão de séries temporais para ampliar a visibilidade logística na ArcelorMittal Brasil. In: ENCONTRO NACIONAL DE ENGENHARIA DE PRODUÇÃO, XL, 2020, Foz do Iguaçu, Paraná. Anais […]. Enegep [S. l.: s. n.], 2020.
TEBALDI, P.C. O que é o algoritmo Holt-Winters e como funciona?. OpServices, fev. 2019. Disponível em: <https://www.opservices.com.br/holt-winters/>. Acesso em: 13 junho 2024.
TUBINO, D. F. Planejamento e controle da produção: Teoria e Prática. 3. ed. São Paulo: Atlas, 2017.
VIANA, J.J. Administração de materiais: um enfoque prático. São Paulo: Atlas, 2002.
WERNER, L.; RIBEIRO, J. L. D. Previsão de demanda: uma aplicação dos modelos Box-Jenkins na área de assistência técnica de computadores pessoais. Revista Gestão & Produção, São Carlos, vol. 10, n 1, p.47-67, abr. 2003.
