REGISTRO DOI:10.5281/zenodo.10791358
Alan de Oliveira Pinto Neves1
RESUMO
O objetivo deste trabalho foi fazer uma análise de uma viga engastada com carregamento uniforme utilizando o método de Euller-Bernoulli e o método de elementos finitos. Na análise pelo método de elementos finitos, foi utilizado um elemento de viga com 2 graus de liberdade para cada nó. Comparando os modelos verificou-se que a solução por elementos finitos para rotação tem um erro de 50% e para deflexão tem um erro 67% comparada com o método de Euller-Bernoulli. Esses erros são devido à análise simplificada utilizada no trabalho.
Palavra-chave: Análise de viga engastada, método de Euler-Bernoulli, Método de elementos finitos.
ABSTRACT
The objective of this work was to analyze an embedded beam with uniform loading using the Euller-Bernoulli method and the finite element method. In the analysis by the finite element method, a beam element with 2 degrees of freedom was used for each node. Comparing the models, it was found that the finite element solution has an error of 50% for rotation and an error of 67% for deflection compared to the Euller-Bernoulli method. These errors are due to simple finite element analysis.
Keyword: cantilever beam analysis, Euler-Bernoulli method, Finite element method.
1 INTRODUÇÃO
A análise de vigas é uma prática fundamental em engenharia, sendo aplicada em uma variedade de projetos, desde edifícios e pontes até máquinas industriais. Esses projetos são meticulosamente concebidos para suportar os esforços aplicados e evitar falhas estruturais. À medida que as cargas externas aumentam gradualmente, a estrutura está sujeita a um ponto de ruptura. Especificamente, quando essas cargas agem perpendicularmente, ocorre uma deformação conhecida como flexão, que pode resultar em deflexão, alterando a posição inicial da viga para outra. Em máquinas e estruturas, quando uma viga com eixo longitudinal reto é submetida a forças laterais, ocorre uma deformação na forma de uma curva, denominada curva de deflexão da viga. Assim, a análise não apenas das tensões, mas também das deflexões é crucial para o projetista. De acordo com Gere e Goodno (2010), “quando uma viga com eixo longitudinal reto é carregada por forças laterais, o eixo é deformado em uma curva chamada de curva de deflexão da viga”. Deve-se notar que qualquer flexão resultará em deflexão devido à natureza elástica dos materiais utilizados. Segundo Hibbeler (2010), “a deflexão é a amplitude dos deslocamentos que o material sofre e o diagrama que mostra esses deslocamentos é chamado de flecha ou linha elástica”. Se um elemento é projetado para evitar o escoamento do material, não ocorrerão deformações plásticas ou fraturas, apesar da deflexão. Para este propósito, os modelos de vigas de Euler-Bernoulli e Timoshenko são comumente considerados na análise de deflexões de vigas. Portanto, o objetivo deste trabalho é:
- Realizar uma análise de deflexão de uma viga engastada sob a ação de um carregamento uniforme.
- Utilizar os modelos de vigas de Euler-Bernoulli e o método de elementos finitos para essa análise.
- Avaliar a amplitude das deflexões resultantes do carregamento uniforme aplicado à viga.
- Comparar os resultados obtidos pelos modelos de Euler-Bernoulli e de elementos finitos, destacando suas vantagens e limitações.
- Contribuir para o entendimento da influência do tipo de modelo utilizado na análise de deflexões de vigas engastadas.
2 REVISÃO BIBLIOGRÁFICA
2.1 Modelo Euler-Bernoulli
As hipóteses para teoria clássica de Euler-Bernoulli ou de flexão pura apresentadas por Gere e Godo (2010) são:
- A viga é prismática;
- O material segue a lei de Hooke;
- As inclinações da curva de deflexão são muito pequenas;
- As deformações cortantes são desprezíveis, ou seja, só são consideradas as deformações devida à flexão pura;
Com essas hipóteses, pode-se chegar à equação apresentada por Gere (2010):
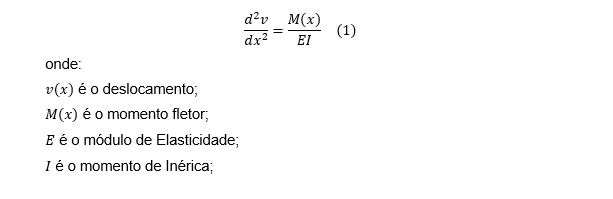
2.2 Formulação do Método de Elementos Finitos
Segundo Bathe (1996), as etapas da formulação do métodos de elementos finitos são:
- Idealização da estrutura por elementos;
- Identificação dos deslocamentos nos pontos nodais;
- Formular as equações de equilíbrio e resolvê-las;
- Obter a distribuição dos deslocamentos pelos elementos;
- Interpretar os resultados;
As estapas para a solução nos programas via elementos finitos são apresentadas pelo seguinte fluxograma conforme ilustra a figura
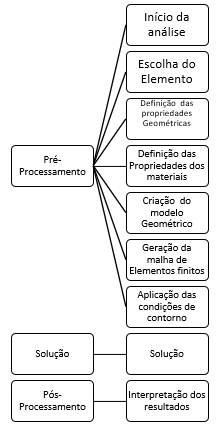
Figura 1 Fluxograma das etapas de elementos finitos. Fonte :Neves (2018)
3 SOLUÇÃO ATRAVÉS DO MODELO DE EULLER-BERNOULLI
3.1 Modelo Euller-Bernouli
A equação apresentada por Gere e Goodno (2010) do modelo Euller-Bernouli é :
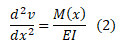
3.1.1 Exemplo:
Será resolvido o problema de uma viga engastada de tamanho L carregamento P distribuído uniformemente com quatro graus de liberdade conforme a figura.
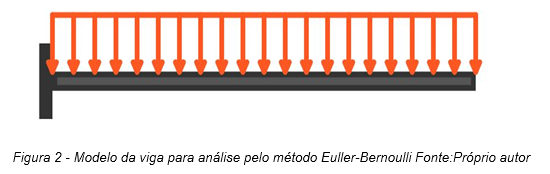
O momento fletor é:
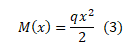
Onde a origem é no engaste com sentido positivo para direita.
Fazendo a primeira integral encontra-se a rotação que segundo Gere e Goodno (2010) é:
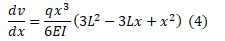
Fazendo a segunda integral encontra-se a deflexão que segundo Gere e Goodno (2010) é:
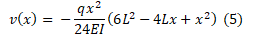
Onde a rotação máxima em x=L é:
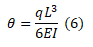
Onde a deflexão máxima em x=L é:
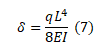
4 SOLUÇÃO ATRAVÉS DO MODELO DE ELEMENTOS FINITOS
Segundo Silva ( 2014, p.14), pode descrever o campo de deslocamentos transversais de um elemento como:

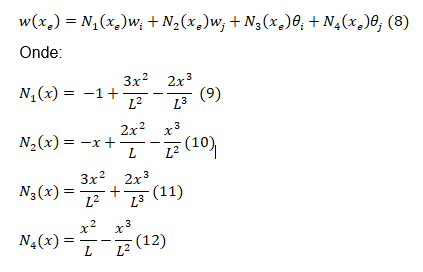

Conforme Silva (2014, p 22), pode-se relacionar a matriz rigidez com os deslocamentos e forças nodais:

Segundo Silva (2014), o vetor de carregamento deve apresentar a carga uniformemente distribuída, o vetor de carregamentos nodais:
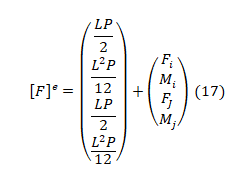
4.1 Exemplo:
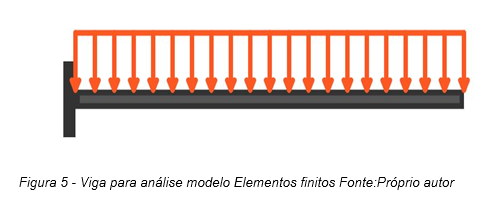
Será resolvido o problema de uma viga engastada de tamanho L carregamento P distribuído uniformemente com quatro graus de liberdade conforme a figura.
Os graus são iguais a zero devido à ao engastamento da viga, logo a as matrizes se reduzem:

5 COMPARAÇÃO ENTRE O MODELO EULLER-BERNOULLI E O MODELO ELEMENTOS FINITOS
Para o problema de uma viga de carregamento P e engastada numa extremidade, a solução do modelo de Euller para rotação máxima x=L encontrada é:
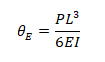
Onde a deflexão do modelo de Euller máxima em x=L é:
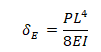
Já para o modelo de elementos finitos a solução para a rotação máxima x=L encontrada é:
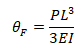
Onde a deflexão do modelo de Euller máxima em x=L é :
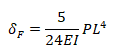
Utilizando a formula abaixo para calcular o erro relativo entre as duas soluções:
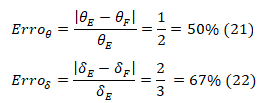
6 CONCLUSÃO:
O erro relativo encontrado na solução de uma viga com carregamento uniforme e engastada pelo método de Elementos finitos foi alto em relação a solução analítica do modelo Euller-Bernouli, porém só foi utilizado um elemento. Logo, a solução não terá uma boa aproximação. Conforme o aumento no número de elementos, a solução no modelo de elementos finitos irá convergir. O objetivo do trabalho era demostrar de maneira simples como funciona o equacionamento do modelo de elementos finitos, porém para verificar essa convergência pode-se utilizar de programas numéricos que utilizam esse método, por exemplo, Ansys e Ftool.
A análise de elementos finitos é apropriada, por exemplo, para ser usada em problemas de vigas estaticamente indeterminada, pois deverá impor as condições de contorno no apoio. Logo para dar continuidade e aprofundar mais nesse assunto, sugere-se como trabalho futuro, a solução de uma viga estaticamente indeterminada com um carregamento uniforme.
7 REFERÊNCIA BIBLIOGRÁFICA
BATHE, Klaus. Finite Element Procedures . 2. ed. [S.l.]: Prentice Hall, 1996. 1065 p. v. 1
GERE, James; GOODNO, Barry. Mecânica dos materiais . 7. ed. Rio de Janeiro: CENGAGE Learning, 2010. 858p
HIBBELER , R. C. Resistência de Materiais . 7. ed. [S.l.: s.n.], 2010. 640 p. v. 1.
NEVES, Alan. ANÁLISE DO EIXO TRASEIRO DE UM KART. In: NEVES, Alan. ANÁLISE DO EIXO TRASEIRO DE UM KART. Orientador: MAURO SPERANZA NETO. 2018. Trabalho de conclusão de curso (Bacharelado) – PUC-RIo, Rio de Janeiro, 2018. p. 83.
SILVA, Alexandre Miguel Rufino. Elemento de viga de formulação mista para aplicações estruturais. Universidade de Aveito. 2014.
1Mestrando no programa de Pós-Graduação em Engenharia mecânica pela PUC-Rio
