ANALYSIS OF INERTIAL OSCILLATIONS IN THE VITÓRIA’S FLOAT
REGISTRO DOI:10.5281/zenodo.12635774
Vinicius Luiz de Lima
Orientador: Albano Ribeiro Alves
Programa: Curso de Aperfeiçoamento em Hidrografia
O estudo das oscilações inerciais torna-se de grande importância no sentido de analisar eventos de caráter destrutivo no oceano, como contaminações de óleos, por exemplo. Em virtude disso, um estudo dessas oscilações em uma boia oceânica, localizada em Vitória (Espírito Santo) foi desenvolvido. Os resultados obtidos pelo ADCP localizado na boia foram filtrados através da série de Fourier, de forma a evidenciar no espectro de frequências as oscilações inerciais. Também foram comparados os períodos e raio teórico e observado das correntes, de forma a comprovar se o modelo matemático proposto é condizente com a realidade observada no oceano. Verificou-se que o período inercial observado foi 6,4% menor que o período inercial teórico, enquanto o raio teórico foi entre 1,7% e 5,9% maior que o raio observado para os dois períodos observados.
Palavras chave: boia de Vitória, oscilações inerciais, ADCP, dados observacionais da corrente.
Department: Hydrography Improvement Course
The study of inertial oscillations becomes very important in order to analyze destructive events in the ocean, such as oil contamination, for example. As a result, a study of these oscillations in an ocean float located in Vitória (Espírito Santo) was developed. The results obtained by the ADCP located in the float were filtered through the Fourier series, in order to show inertial oscillations in the frequency spectrum. The theoretical and observed radius and periods of the currents were also compared, in order to prove if the proposed mathematical model is consistent with the reality observed in the ocean. The observed inertial period was 6.4% shorter than the theoretical inertial period, while the theoretical radius was between 1.7% and 5.9% greater than the observed radius for the two observed periods.
Keywords: Vitoria’s float, Inertial Oscillations, ADCP, observational data of the current.
1 – Introdução
O movimento inercial pode ser descrito como o movimento que, após um impulso, se perpetua graças à inércia de um determinado material. No caso de correntes oceânicas, o impulso necessário pode ser, por exemplo, o vento incidente sobre o oceano por algumas horas. Quando isso ocorre, a água tende a se mover devido à influência da força de Coriolis e da gravidade. A água tende a continuar se movendo devido à sua massa, e esse movimento é o que define o conceito de corrente inercial (Stewart).
As correntes inerciais foram observadas primeiramente por Helland-Hansen e Ekman (1931). Essa observação foi feita através de informações analisadas em uma estação oceanográfica no Atlântico que estava ancorada em uma região sob forte ação de ventos alísios. Com o decorrer do tempo, análises mais profundas começaram a ser realizadas, o que gerou diversos estudos de forma a estabelecer os princípios que sustentam esses movimentos. Poulain (1990) e Alves (1992) comprovaram que os movimentos inerciais possuem relevância significativa na cascata de energia dos oceanos.
A importância do estudo de oscilações inerciais se mostra mais evidente ao analisar a contribuição da energia advinda dessas oscilações em relação à energia total do oceano. Young e Jelloul (1997) comprovaram que a energia dessas oscilações corresponde à aproximadamente metade da energia cinética do oceano. A investigação dos fenômenos que permeiam as oscilações inerciais torna-se de extrema importância para a identificação da trajetória de objetos na superfície oceânica, ou, ainda, para contenção de poluentes no oceano, em caso de derramamento de óleos, por exemplo. Um exemplo de medição e acompanhamento de oscilações inerciais é observado na figura 1.
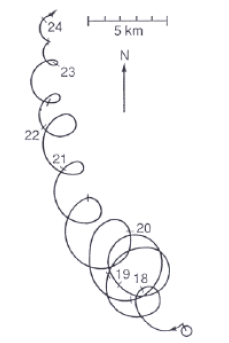
Figura 1: Diagramas vetoriais obtidos a partir de dados correntográficos para observação de oscilações inerciais no Mar Báltico. Os números representam os dias do mês. Fonte: Gustafson & Kullenberg (1936).

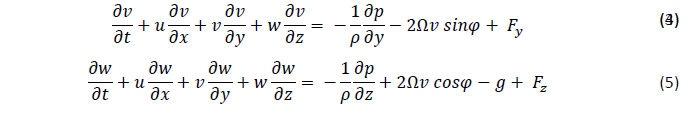

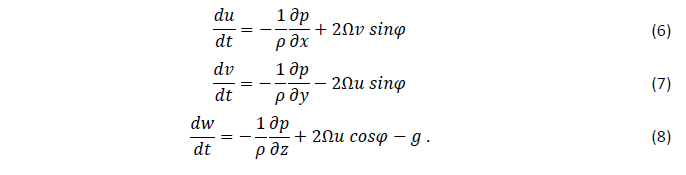
Assumindo também que a gravidade e a força de Coriolis são as únicas forçantes de movimento, pode-se inferir que


As oscilações inerciais interagem com o fluxo básico e produzem variações de frequência inercial local. Essas variações são oriundas do efeito Doppler gerado por essa interação, que faz com que haja um desvio da frequência inercial local em direção às maiores frequências. Isso ocorre devido ao efeito da vorticidade do fluxo e faz com que a frequência inercial efetiva seja diferente da frequência inercial local, sendo, portanto, maior para um movimento anti-ciclônico (Leite, 2014). A relação entre as frequências teórica e efetiva é mostrada pela equação (18), que é

onde u e v são as componentes horizontais de velocidade para as direções x e y, respectivamente (Mooers [1975], Perkins [1976]).
Para a correta análise das oscilações inerciais, é necessário separá-las das correntes de maré. As correntes de maré em plataformas continentais que possuem latitude semelhante à plataforma base para o estudo descrito neste trabalho, localizam-se em faixas de frequência bastante próximas às faixas espectrais das oscilações inerciais. Dessa forma, torna-se necessário subtrair as correntes de maré da amostra total através da análise de Fourier.
A análise de Fourier consiste em um método matemático para representar sinais complexos como sobreposições de sinais sinusoidais. Para isso, as funções são representadas como séries infinitas de senos e cossenos. Qualquer função pode, portanto, ser representada pela forma

Quanto maior o valor de n, ou seja, quanto maior a ordem da série harmônica, mais aproximada será a sobreposição sinusoidal em relação à função original. Um exemplo de aproximação com aumento de ordem da série de Fourier é mostrado na figura 2.
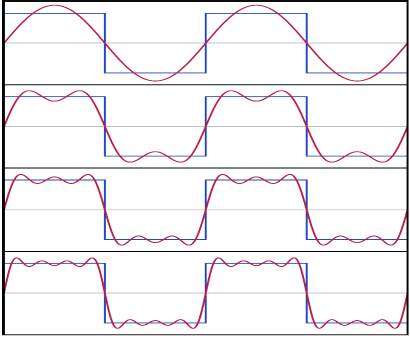
Figura 2: Primeiras quatro somas da série de Fourier de uma onda quadrada. Fonte: Wikipedia (2007).
Através da série de Fourier, é possível separar as correntes de maré mais energéticas, com amplitudes próximas às definidas por autores como De Mesquita e Harari (2003). Após esse procedimento, é possível extrair essas correntes do espectro total, o que resulta no espectro das correntes inerciais.
Na prática, a medição de período das correntes oceânicas é feita através de boias oceânicas, que são equipamentos alocados na superfície oceânica que têm como objetivo receber dados ambientais a respeito do mar, tais como temperatura da água, umidade relativa do ar, temperatura do ar, temperatura do ponto de orvalho, radiação solar, além das informações das correntes propriamente ditas. Essas informações são extremamente importantes para análise de eventos como, por exemplo, vazamentos de óleo no oceano. Através dessa medição, é possível prever a trajetória percorrida pelo óleo no oceano, e, assim, facilitar o processo de contenção da contaminação.
Para a medição de dados das correntes oceânicas, as boias são equipadas com um equipamento denominada ADCP (do inglês, Acoustic Doppler Current Profiler). Esse equipamento mede a velocidade de partículas na coluna de água através do Efeito Doppler, que é o efeito observado em ondas quando o objeto emissor da mesma está em movimento em relação ao observador. Um exemplo de ADCP é mostrado na figura 3.

Figura 3:exemplo de ADCP. Fonte: Seatronics (2013)
O ADCP fica acoplado no casco da boia, a uma distância de 0,5m da linha d’água. Esse equipamento fica apontado para baixo, e, com isso, é possível capturar dados das correntes de até 60 metros de profundidade. Uma representação do processo é apresentada a seguir.
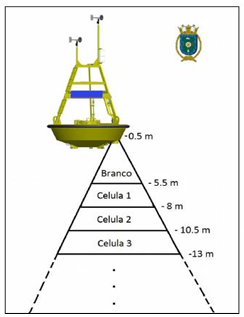
Figura 4: Representação esquemática da medição das correntes com a boia, onde está acoplado o ADCP. Fonte: Marinha do Brasil (2016).
O tempo necessário para a execução de um ciclo de medição da boia é de 1 hora. Nos primeiros 5 minutos, as informações de posição da boia são coletadas, bem como os dados do ADCP. Até os 10 minutos de medição, são coletadas todas as informações meteorológicas e oceanográficas da boia. Até os 20 minutos, a boia consegue coletar os dados das ondas. A partir desse momento, a boia leva 10 minutos para processar os dados e enviá-los para a rede de satélite. Após esse período, há um momento de stand by do equipamento por 30 minutos, com o objetivo de aumentar a longevidade do equipamento.
No presente trabalho, o principal objetivo é analisar os dados do ADCP de uma boia em específico e comparar os resultados obtidos para período e raio das correntes inerciais com os resultados efetivamente observados na boia.
A boia de estudo para este trabalho foi a boia de Vitória, localizada no estado do Espírito Santo. Essa boia possui diâmetro de 3,4 metros, peso de 1500 kg e profundidade de fundeio de 200 metros, conforme informação do PNBOIA (2016).
O PNBOIA (Programa Nacional de Boias) iniciou-se em 1996 através de um grupo de especialistas em meteorologia e oceanografia. O objetivo do programa é ampliar o sistema de coleta de dados oceanográficos através das boias e aperfeiçoar, dessa forma, os serviços de meteorologia e de oceanografia no Brasil, que são extremamente úteis nas áreas de agricultura, petróleo, transportes, entre muitos outros (Marinha do Brasil, 2016). O PNBOIA lançou um total de 12 boias desde agosto de 2000, quando a primeira boia foi lançada, na costa do Rio Grande do Sul. Dessas 12 boias, 3 se localizam na região Nordeste (Fortaleza, Recife e Porto Seguro), 6 na região Sudeste (Itaoca, Vitória, Santos, 2 em Cabo Frio e 2 em Niterói) e 2 na região Sul (Rio Grande e Itajaí).
A boia de Vitória, foco deste estudo, e sua localização geográfica, são mostradas nas Figura 5 e 6.

Figura 5: Boia de Vitória. Fonte: Marinha do Brasil (2016).
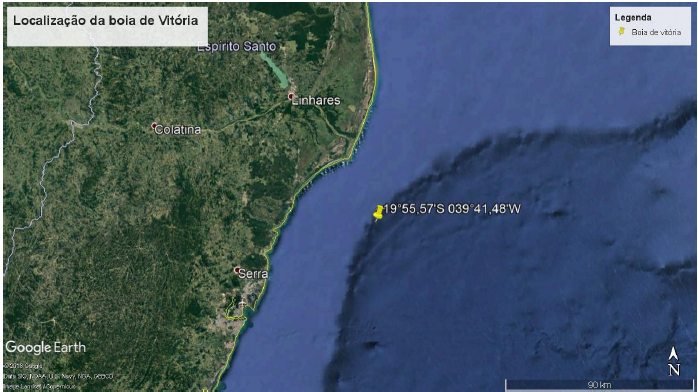
Figura 6: Localização geográfica da boia de Vitória. Fonte: Google Earth (2019)
No decorrer deste documento, será mostrada a metodologia para obtenção dos resultados, utilizando os dados do ADCP para extração das velocidades, bem como os procedimentos numéricos para obtenção das informações do raio e do período das correntes inerciais. Após essa apresentação, será mostrada a comparação dos dados obtidos com os dados observados nos períodos de medição pela boia. Também serão apresentadas as análises dos resultados, com o objetivo de validar a acurácia da metodologia proposta.
Este documento foi organizado em 4 capítulos. No capítulo 2, a metodologia de análise para obtenção dos resultados é mostrada, enquanto no capítulo 3 são apresentados os principais resultados obtidos, bem como a análise dos mesmos. No capítulo 4 tem-se as conclusões extraídas a partir dos resultados obtidos.
2 – Metodologia
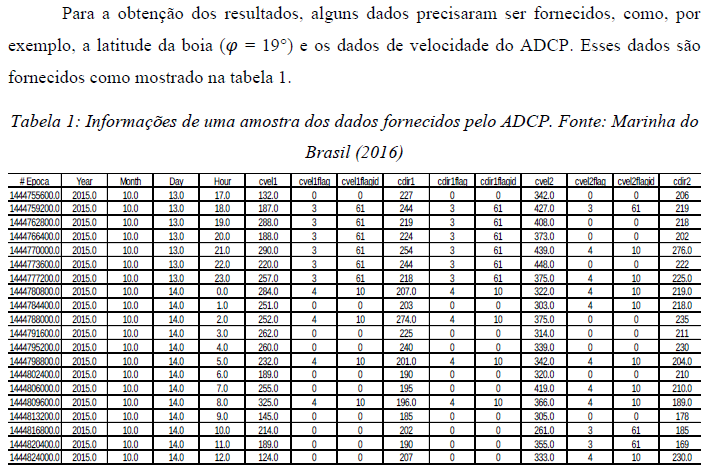

Após isso, as componentes de velocidade cveli foram submetidas à análise de Fourier prevista pela equação (20), da qual foram extraídos os coeficientes de Fourier, que são determinados pelas equações (21), (22) e (23), descritas anteriormente.
Os resultados obtidos pela análise de Fourier foram submetidos, dessa vez, a um filtro passa-banda com janela de largura entre 20% abaixo do período inercial calculado, e 10% acima do mesmo. A partir dessa janela de períodos, foi possível definir a faixa de frequências de interesse, visto que a frequência é equivalente ao inverso do período. Esses limites de frequência, divididos pela frequência fundamental, correspondem aos limites superior e inferior do somatório nas equações de Fourier. Com essas informações, a série de Fourier foi novamente aplicada, utilizando a equação (20). Assim, foi possível reconstruir o sinal da oscilação inercial, pois, graças a essa filtragem, as frequências subinerciais (acima de 10% do período inercial) e de maré (abaixo de 20% do período inercial) foram eliminadas, visto que se encontram fora da faixa de período extraída.
Após análise de Fourier, o período da corrente inercial foi observado para todas as componentes de velocidades e a metodologia de análise dos dados foi efetuada levando em consideração apenas um determinado período de tempo. Foi observado que, no período entre o dia 24 de outubro de 2015, às 16 horas, e o dia 26 de outubro de 2015, às 01 hora (um período, portanto, de 33 horas), as componentes norte, sul, leste e oeste da velocidade completavam um ciclo, formando uma onda sinusoidal. Isso também foi verificado no intervalo entre 26 de outubro de 2015, às 1 horas, e 27 de outubro de 2015, às 10 horas (período de 34 horas). Essas faixas de período foram extraídas e a velocidade média foi subtraída das componentes de velocidade para cada instante de tempo. Multiplicando cada componente resultante dessa subtração pelo tempo (que, para a boia selecionada, é de uma hora), foram definidos vetores que descrevem a trajetória das partículas devido ao movimento inercial. Esses vetores formam uma trajetória que foi representada graficamente, com o intuito de analisar o comportamento da corrente. Através dessa construção gráfica, foi possível extrair, também, o raio observado para os dois períodos de tempo.
A próxima etapa do procedimento foi a de calcular o período e o raio teóricos da boia. Para efetuar o cálculo do período, tendo as informações de velocidade de rotação da Terra e a latitude local, foi necessário utilizar a equação (16), descrita anteriormente.
Com a obtenção da velocidade média das componentes de velocidade obtidas através da análise de Fourier, foi possível obter o raio teórico do modelo proposto. Esse resultado foi obtido através da equação (17).
3 – Resultados e Análises
Após a análise das componentes de velocidade para as direções Norte/Sul e Leste/Oeste no período entre o dia 24 de outubro de 2015, às 16 horas, e o dia 26 de outubro de 2015, às 01 hora (que será denotado por período 1), o gráfico mostrado na Figura 7 foi construído, comprovando o sinal sinusoidal das componentes de velocidade.
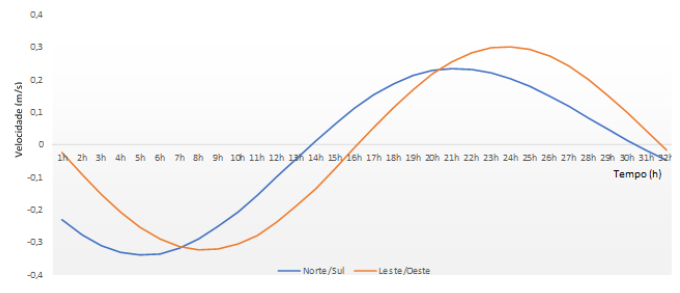
Figura 7: Gráfico das componentes de velocidade (eixo das ordenadas) em relação ao tempo, em horas (eixo das abcissas) para o período observado. Fonte: O autor.
O mesmo procedimento foi realizado para o período entre 26 de outubro de 2015, às 1 hora, e 27 de outubro de 2015, às 10 horas (que será denotado por período 2), obtendo-se o mostrado na Figura 8.
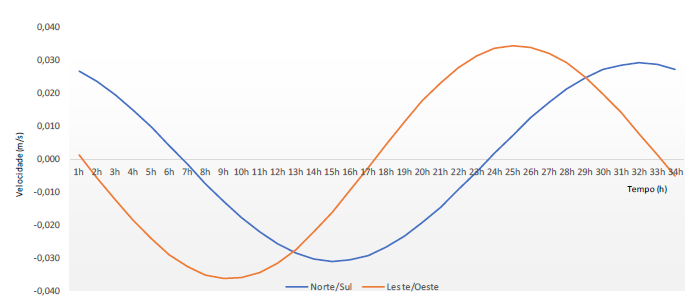
Figura 8: Gráfico das componentes de velocidade (eixo das ordenadas) em relação ao tempo, em horas (eixo das abcissas) para o período observado. Fonte: O autor.
O cálculo do período teórico das oscilações inerciais para a boia apresentada neste estudo é realizado utilizando-se a equação (15), onde se obtém
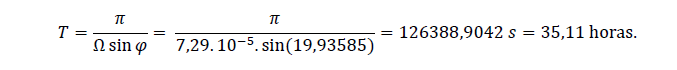
A comparação entre o período teórico e o período observado é mostrada na Tabela 2.
Tabela 2: Comparação entre período calculado e período observado. Fonte: O autor

A dispersão entre o resultado observado e o resultado calculado está dentro do intervalo estabelecido por Kundu (1976) para diminuição percentual do período inercial efetivo, que está na faixa entre 2% e 20%. O motivo para tal dispersão é a interação entre a oscilação inercial e o fluxo básico descrita na introdução deste documento. Graças ao aumento de frequência, o período observado diminui, o que gera uma dispersão positiva entre os períodos observado e calculado.
É importante ressaltar que a tendência de redução do período inercial efetivo em detrimento ao período inercial local se dá devido ao fato de a vorticidade da corrente ser anticiclônica, característica da região de medição da boia. Se a vorticidade fosse no sentido oposto (ciclônica), a frequência inercial se deslocaria para baixas frequências, fazendo com que período inercial efetivo fosse maior que a período inercial local.
Após a determinação do período inercial, foram determinados os limites superior e inferior do filtro passa banda, que são de 38.62 h e 28.09 h, respectivamente. Realizada essa filtragem dos dados do ADCP, conforme explicitado na seção de metodologia, as correntes inerciais foram extraídas da corrente total para as direções norte, sul, leste e oeste, via série de Fourier. Como resultado, temos o mostrado nas figuras 9 e 10.
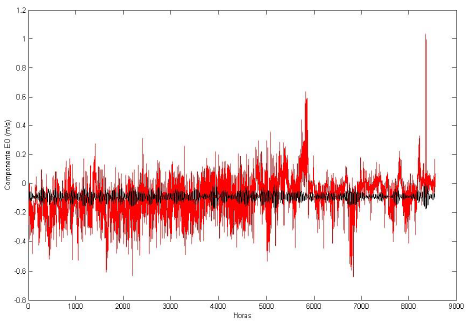
Figura 9: Comparação entre as componentes leste e oeste da corrente observada (vermelho) e filtrada (preto). Fonte: O autor
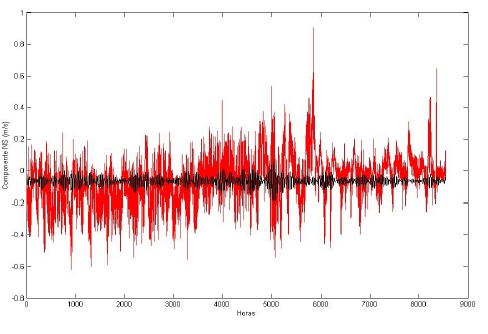
Figura 10: Comparação entre as componentes norte e sul da corrente observada (vermelho) e filtrada (preto). Fonte: O autor
As correntes filtradas, representadas pelas áreas pretas das figuras 9 e 10, foram as consideradas para a obtenção dos resultados deste trabalho.
Foi realizada também uma análise gráfica da série de velocidades das oscilações inerciais. Esse tipo de análise permite separar as correntes com rotação anti-ciclônica (que são as correntes inerciais propriamente ditas), daquelas de rotação ciclônica na mesma faixa de frequência. Para isso, foram traçados vetores de velocidade com relação ao tempo (que são representados pelos gráficos pretos nas figuras 11, 12 e 13) e, desses, foram extraídos os vetores de trajetória ciclônica e anti-ciclônica. Para facilitar a visualização, os gráficos em vermelho representam a extremidade dos vetores de velocidade para cada instante, mostrando as características de rotação do gráfico analisado. Por fim, as componentes vetoriais do vento também foram representadas. Todas as informações decorrentes dessa análise para o primeiro período de análise (período 1) foram representadas em gráficos onde, no eixo das abscissas, tem se o tempo, e, no eixo das ordenadas, tem-se a velocidade, como mostrado nas figuras 11, 12 e 13.
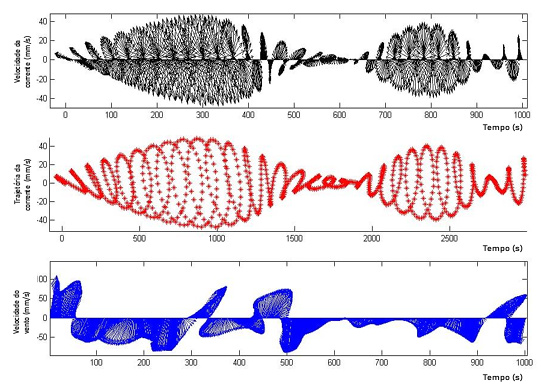
Figura 11: Vetores de velocidade em relação ao tempo das oscilações anti-ciclônicas da corrente observada, extremidade dos vetores e vetores de vento. Fonte: O autor.

Figura 12: Vetores de velocidade em relação ao tempo das oscilações ciclônicas que ocorrem dentro da faixa de frequência inercial da corrente observada no período 1, extremidade dos vetores e vetores de vento. Fonte: O autor.
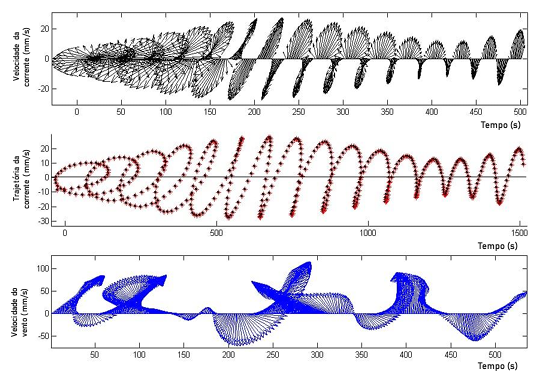
Figura 13: Transição entre os vetores das correntes de trajetória ciclônica e anti-ciclônica. Fonte: O autor.
Já a análise decorrente desse processo para o segundo período de observação (período 2) é mostrada nas figuras 14 e 15.
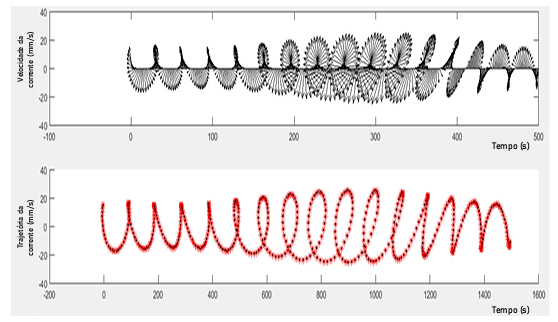
Figura 14: Vetores de velocidade em relação ao tempo das oscilações anti-ciclônicas que ocorrem dentro da faixa de frequência inercial da corrente observada no período 2 e extremidade dos vetores. Fonte: O autor.

Figura 15: Vetores de velocidade em relação ao tempo das oscilações ciclônicas que ocorrem dentro da faixa de frequência inercial da corrente observada no período 2, extremidade dos vetores e vetores de vento. Fonte: O autor.
O próximo passo consistiu em determinar o raio observado e o raio teórico das oscilações. Para a determinação do raio observado, foi necessário aproximar o gráfico da trajetória de partículas, cuja metodologia de construção foi explicada anteriormente, para um formato elíptico e, depois, extrair a média entre os semi-eixos maior e menor. Essa média foi de 0,925 km, analisando-se o período 1, e de 0,900 km para o período 2. Os gráficos com os vetores que definem a trajetória das partículas devido ao movimento inercial para os dois períodos de observação são representados na figura 16.
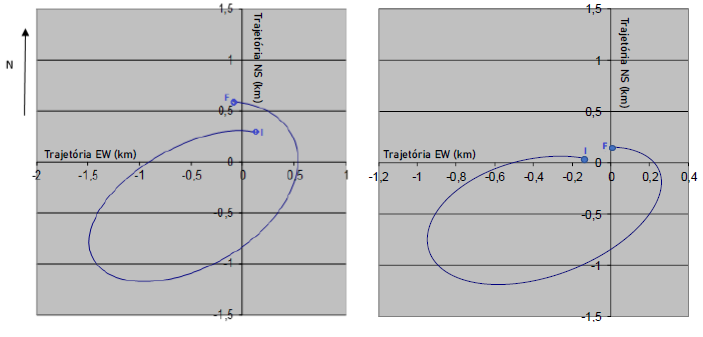
Figura 16: Representação da trajetória das partículas devido à oscilação inercial para os dois períodos de observação. O eixo das abcissas corresponde à trajetória nos sentidos leste/oeste, em quilômetros, enquanto o eixo das ordenadas representa as trajetórias nos sentidos norte/sul, também em quilômetros. Os pontos I e F representam, respectivamente, o início e o fim da trajetória. Fonte: O autor.
Para obtenção do raio teórico para a oscilação inercial analisada, denotados por R1 e R2 (onde os números representam o período observado), foi necessário utilizar a equação (16), conforme citado na seção de metodologia, a partir das informações de velocidade média para os períodos 1 (0,049 m/s) e 2 (0,044 m/s), obtendo-se, dessa forma,
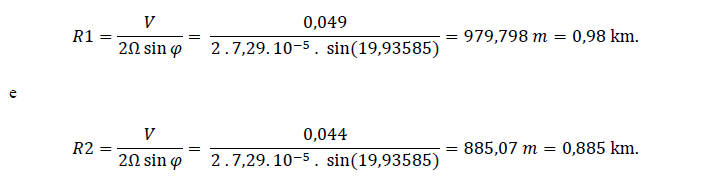
A comparação entre o raio teórico e o raio observado para o modelo proposto é apresentada na Tabela 3.
Tabela 3: Comparação entre raio calculado e raio observado. Fonte: O autor.

A dispersão entre o raio calculado e o raio observado deve-se, principalmente, ao fato de, devido à vorticidade do fluxo básico, a trajetória da corrente não ser perfeitamente circular, mas sim elíptica. Dessa forma, a média entre os semi-eixos realizada representa um raio observado aproximado.
4 – Conclusões
De acordo com os resultados obtidos com os estudos realizados neste trabalho, pode-se concluir que o método matemático para análise de oscilações inerciais é fidedigno à realidade para a boia estudada. Os resultados teóricos e observados para o período inercial e para o raio da oscilação da corrente inercial apresentaram divergências menores que 7%, valores já previstos devido ao efeito vorticidade.
Além disso, foi demonstrado através do código computacional que a aproximação via série de Fourier da função que rege o movimento inercial para o caso apresentado foi bastante próxima à função original. Pode-se inferir que, se os valores fornecidos pela ADCP fossem discretizados em intervalos menores (intervalos de 30 minutos, por exemplo), os resultados obtidos seriam ainda mais próximos da realidade.
Foi percebido também que a tratativa das componentes de velocidade utilizando o filtro passa banda mostrou-se determinante para uma boa aproximação dos resultados teórico e observado deste estudo, visto que a ocorrência de marés prejudica a análise das correntes inerciais propriamente ditas. A retirada dessa influência foi de extrema importância para a análise fidedigna das oscilações.
Como oportunidades para trabalhos futuros, algumas questões ainda podem ser respondidas, como, por exemplo, se o modelo matemático continua sendo aplicável se a boia é submetida a condições mais abruptas de vorticidade, como pode acontecer em outras boias. Nesses casos, como a frequência efetiva pode aumentar ou diminuir muito em relação à frequência inercial local, é necessário compreender o campo de aplicação do modelo, não só com relação às diferentes boias, mas até mesmo com relação aos diferentes oceanos. Embora o Brasil possua fronteira exclusiva com o oceano Atlântico, oceanos como o Pacífico e o Índico também são rotas de transporte para produtos que são importados pelo país. Portanto, a análise desses fenômenos torna-se importante até mesmo para a economia do Brasil.
5 – Referências Bibliográficas
Alves, M. A., 1992: Correntes de maré e inerciais na plataforma continental ao largo de Ubatuba (SP). Dissertação de Mestrado, Universidade de São Paulo, São Paulo, 162 pp.
Google Earth, 2019: Mapas. Disponível em: <https://www.google.com.br/maps>. Acesso em: 25 set. 2019.
Gustafson, T. & B. Kullenberg, 1936: Untersuchungen von Trägheitsströmungen in der Ostsee. Svenska Hydrogr. Biol. Komm. Skrifter, Ny Ser. Hydrogr., (13), 1–28.
Helland-Hansen, B. & V. W. Ekman, 1931: Measurements of ocean currents (Experiments in the North Atlantic). Kungl. fysiografiska Sällskapet i Lund Förhandlingar, 1(1).
Kundu, P. K., 1976: An analysis of inertial oscillations observed near the Oregon Coast. J. Phys. Oceanogr., 6, 879–893.
Leite, J. R. B., 2014: Correntes Inerciais sobre a Plataforma Continental Sudeste do Brasil. Tese (Doutorado em Oceanografia Física) – Instituto Oceanográfico da Universidade de São Paulo, São Paulo, 136 pp.
Marinha do Brasil, 2016: Boia Vitória – Centro de Hidrografia da Marinha. Disponível em <https://www.marinha.mil.br/chm/dados-do-pnboiaboias/boia-vitoria>. Acesso em 03 jun. 2019
Mooers, C. N. K., 1975: Several effects of a baroclinic current on the cross-stream propagation of inertial-internal waves. Geophys. Fluid Dyn., 6, 245–275.
Perkins, H., 1976: Observed effect of an eddy on inertial oscillations. Deep Sea Research and Oceanographic Abstracts, 23(11), 1037 – 1042.
Poulain, P., 1990: Near-inertial and diurnal motions in the trajectories of mixed layers drifters. J. Mar. Res., 48, 793–823.
Wikipédia, 2007: Série De Fourier. Disponível em: <https://pt.wikipedia.org/wiki/ Série_de_Fourier>. Acesso em: 03 set. 2019. Seatronics, 2013. Teledyne RDI Workhorse Sentinel ADCP. Disponível em:<https://seatronics-group.com/equipment-rental/metocean/adcp/teledyne-rdi-workhorsesentinel-adcp/>. Acesso em: 06 set. 2019
Stewart, R. H. Introduction To Physical Oceanography. Department of Oceanography. Texas A & M University. Copyright 2002. Spring 2002 Edition, 107 – 118
Young, W. R. & B. M. Jelloul, 1997: Propagation of near-inertial oscillations through a geostrophic flow. J. Mar. Res., 55, 735–766.
