REGISTRO DOI: 10.5281/zenodo.7626667
Eliomar Gotardi Pessoa
Gabriel Seixas Pinto Azevedo Benittez
Nathalia Pizzol de Oliveira
Vitor Borges Ferreira Leite
Resumo: Muitos fenômenos físicos que ocorrem na natureza, em especial na Engenharia Civil, podem ser modelados por equações diferenciais. O cálculo de deflexão de estacas isoladas submetidas a carregamento horizontal, foco de estudo neste trabalho, é modelado por uma equação diferencial linear de quarta ordem, a qual pode ser resolvida por métodos analíticos e numéricos. Os autores trataram o fenômeno de interação solo-estaca por meio das abordagens de WINKLER (1867) e PASTERNAK (1954), e propuseram a resolução analítica das equações diferenciais através da Transformada de Laplace e da Equação Característica da EDO de coeficientes constantes. Por fim, os resultados teóricos foram comparados com os experimentais, realizados na FEC/Unicamp, e com os encontrados pelo programa SAP 2000. Foi verificada grande concordância entre todos os resultados.
Palavras-chave: Equação diferencial. Estaca. Interação solo-estaca. Transformada de Laplace.
1 Introdução
1.1 Considerações Iniciais
Na maior parte dos casos, as estacas são carregadas com forças axiais, porém de acordo com o carregamento aplicado, estas podem estar submetidas à forças horizontais. As torres de linhas de transmissão e os pilares de ponte são exemplos nos quais suas fundações são solicitadas por forças horizontais devido à atuação do vento nessas estruturas esbeltas. Suas fundações são, usualmente, estacas ou tubulões que terão uma carga horizontal aplicada em seu topo. Sendo assim, o estudo do comportamento de estacas submetidas a esforços horizontais tem grande relevância no estado da arte da Engenharia Geotécnica, uma vez que são estruturas utilizadas com recorrência em projetos dessa área.
1.2 Objetivo
O presente trabalho tem como objetivo a utilização de métodos matemáticos para determinar os deslocamentos de uma estaca escavada isolada submetida a provas de carga estática horizontal, simulando a interação solo-estaca. Os ensaios foram realizados no Campo Experimental de Mecânica dos Solos da Unicamp, no qual o subsolo é caracterizado como silto-arenoso.
1.3 Metodologia
Vários métodos diferentes de análise foram propostos para caracterizar o problema. Neste presente trabalho, os autores escolheram os métodos de WINKLER (1867) apud ROSENDO (2020) e PASTERNAK (1954) apud ROSENDO (2020).
O modelo mais utilizado é o estabelecido por WINKLER (1867), que substitui o solo por uma série de molas horizontais. O solo ao redor de uma estaca carregada horizontalmente é solicitado em compressão de um lado, e seria por tração do outro. Como o solo não resiste à tração, a estaca tende a se descolar do solo no lado que estaria tracionado. Assim, um modelo de meio elástico contínuo não representa de maneira adequada o solo em torno dessa estaca. Por esse motivo, e pela maior simplicidade, o modelo de WINKLER (1967) é mais utilizado na prática.
O modelo de PASTERNAK (1954) é baseado no modelo de WINKLER (1967), no entanto contempla a resistência ao cisalhamento entre as camadas de solo, a qual é negligenciada pelo último autor referenciado. Essa resistência é adicionada a fim de considerar a interação entre os elementos da mola na direção vertical.
Como os problemas dessa natureza são modelados com base em equações diferenciais, os métodos escolhidos para a resolução deles são: Transformada de Laplace e Equação Característica da EDO de coeficientes constantes.
Também foram realizadas análises paramétricas com o objetivo de identificar o efeito da variação da carga aplicada e do diâmetro da estaca nos deslocamentos.
Por fim, os resultados teóricos foram comparados com a análise realizada através da ferramenta SAP 2000 pelos autores do trabalho e com os dados da instrumentação fornecidos por ROSENDO (2020).
2 Caso estudado
2.1 Parâmetros utilizados
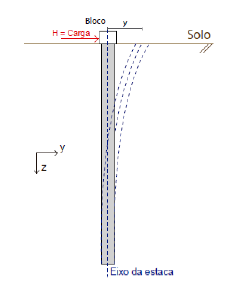
O caso estudado no presente trabalho é o de uma estaca isolada com diâmetro (D) de 30 cm e comprimento (L) de 5 m submetida à provas de carga no Campo Experimental de Mecânica dos Solos da Unicamp, no qual o subsolo é caracterizado como silto-arenoso. Cabe lembrar que alguns dados foram consultados nos trabalhos de MARZOLA (2016) e ROSENDO (2020). No topo da estaca será aplicada uma carga horizontal (H) de 14 kN sem momento (M) aplicado, e o que procuramos encontrar é o deslocamento (y) da estaca em função da profundidade, conforme a figura 1, abaixo.
Figura 1. Estaca isolada sob carregamento horizontal H no topo
Além desses parâmetros, é importante definir o módulo de elasticidade da estaca (Ep) e seu momento de inércia (Ip), apresentados a seguir.
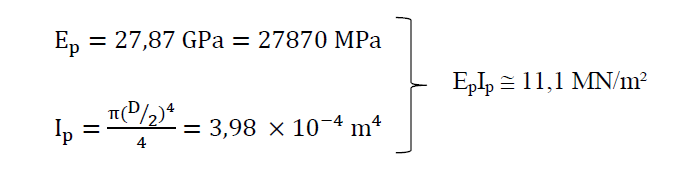
No modelo de Winkler, a reação do solo é dada pelo módulo de reação do solo (K), que pode ser constante ou variar com a profundidade, nesse trabalho adotaremos ele como constante com valor de 13,7 MN/m³. Além disso, é preciso definir o módulo de elasticidade do solo (Es) e o e cisalhamento (G), apresentados abaixo.
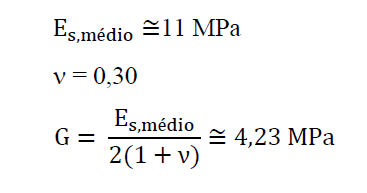
Todos os parâmetros adotados estão em acordo com as características reais de ensaios realizados em estacas isoladas carregadas horizontalmente. Para os cálculos a seguir, as dimensões estão em m e MN.
2.2 Modelo de Winkler
O modelo de Winkler é o que descreve o comportamento do solo de forma mais simplificada, admitindo a hipótese que o solo é modelado como uma série de molas, espaçadas e independentes com comportamento elástico linear. Nesse modelo, as propriedades do solo são descritas apenas pelo parâmetro K, que representa a rigidez da mola.
Esse modelo é considerado uma aproximação do verdadeiro comportamento do solo, principalmente devido à desconsideração da continuidade e da coesão do solo. O modelo matemático para uma estaca isolada, considerando o carregamento no topo da estaca e solo elástico-linear, adotando a hipótese de Winkler para a reação do solo, e considerando a estaca uma viga de Bernoulli, é dado por uma equação diferencial ordinária, onde a primeira parte corresponde à deflexão da estaca e o segundo termo, à hipótese de Winkler, da forma:

Onde,
K – módulo de reação horizontal do solo;
EpIp – rigidez da estaca;
y – deflexão da estaca ao longo da profundidade z.
Com base na teoria de Euler para vigas, são definidas as seguintes Equações:

Considerando uma estaca livre no topo, as condições de contorno em z=0 (topo) são:
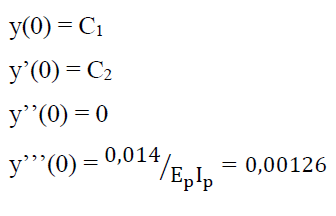
A transformada de Laplace pode ser aplicada a derivadas de infinitos graus, estas sendo contínuas para todo z>0 e se fN é contínua por partes e de ordem exponencial em [0,ꚙ), então:
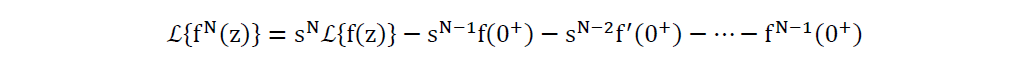
Aplicando a propriedade apresentada será aplicada à equação diferencial da deflexão da estaca (2.1), resultando em:
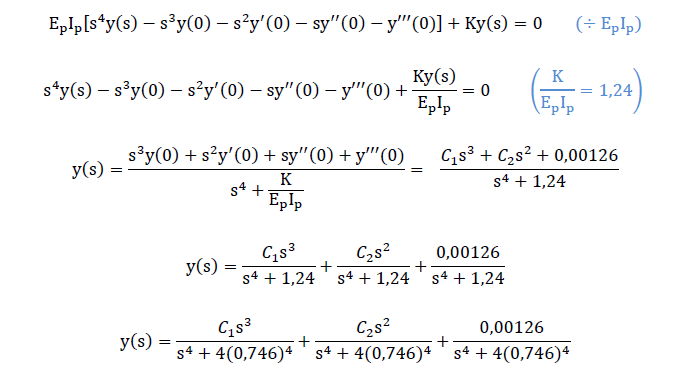
As inversas das transformadas de Laplace foram consultadas em SPIEGEL e LIU (2009):
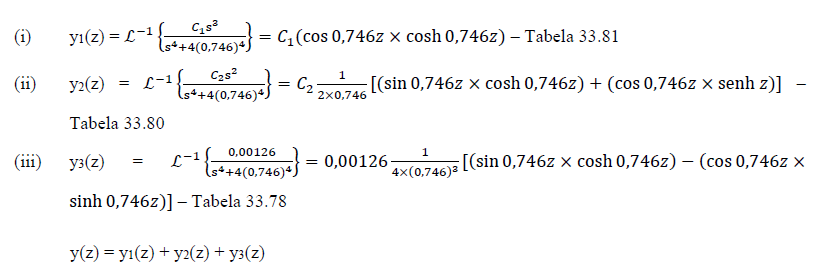
Derivadas:

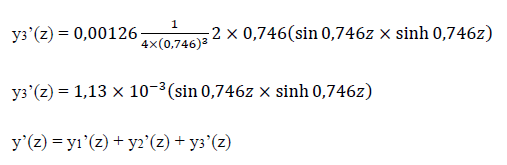
Aplicando as condições de contorno em que y(5) = 0 e y’(5) = 0:
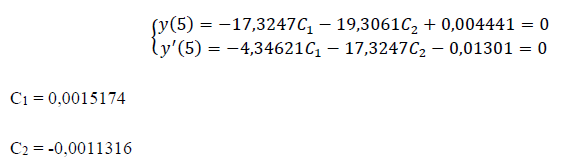
Como os valores das constantes são, agora, conhecidos, pode-se estabelecer o padrão dos deslocamentos horizontais em função do comprimento da estaca devido a aplicação de uma força horizontal de 14kN no topo, conforme a Tabela 1 e a Figura 2.
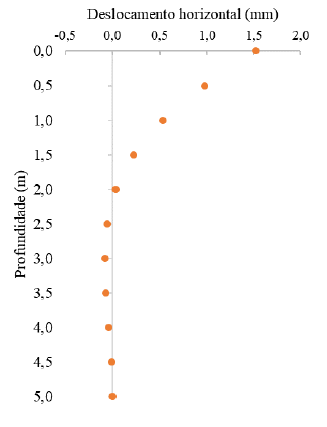
Tabela 1. Valores de deslocamento ao longo do comprimento da estaca – Winkler.
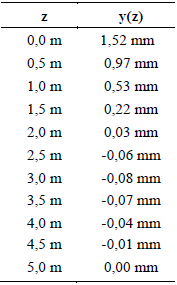
Figura 2. Deslocamento horizontal vs profundidade – Winkler.
2.2.1 Análise paramétrica – variação da carga horizontal aplicada no topo da estaca
Para o estudo paramétrico, supomos aplicação de carga com outros valores: 10kN, 12kN, 16kN, 18kN e 20 kN. Como a carga só produz efeito na terceira parcela da equação diferencial, os sistemas de equações formados pela aplicação das condições de contorno possuem os mesmos valores dos coeficientes que acompanham C1 e C2.
• P = 10 kN
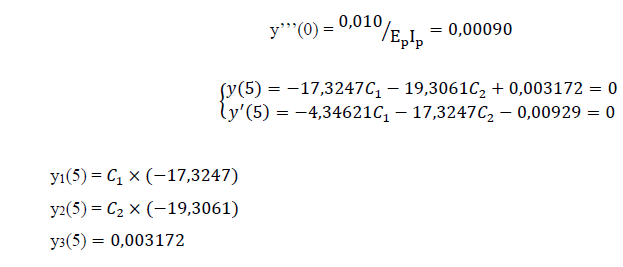
Derivadas:
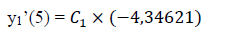
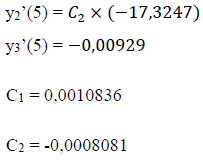
• P = 12 kN
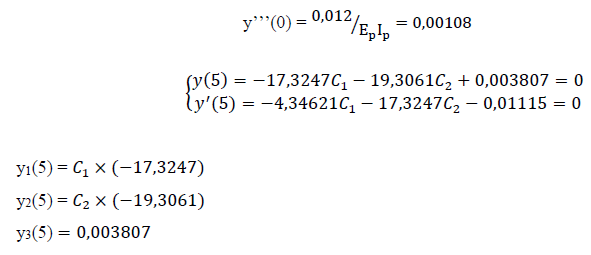
Derivadas:
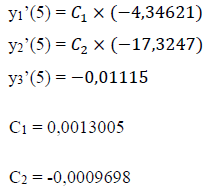
• P = 16 kN
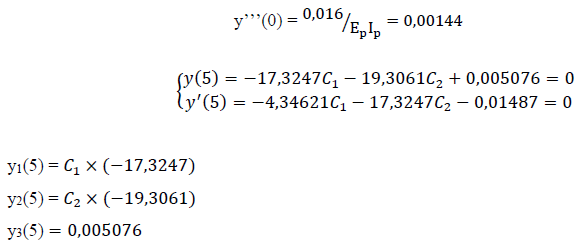
Derivadas:
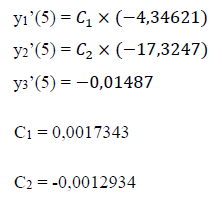
• P = 18 kN
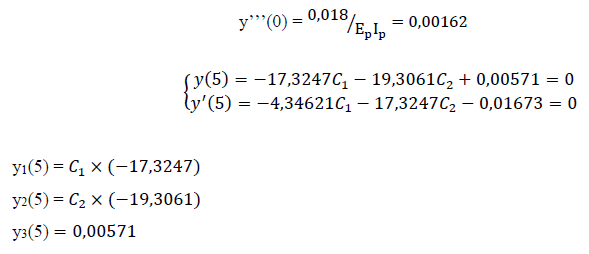
Derivadas:
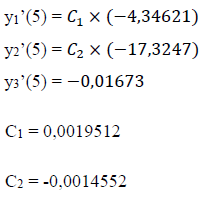
• P = 20 kN
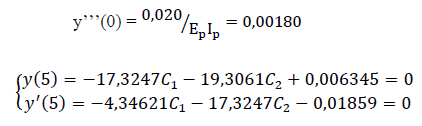
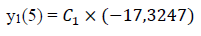
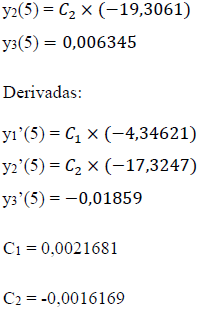
Tabela 2. Valores de deslocamento ao longo do comprimento de estacas com diferentes diâmetros
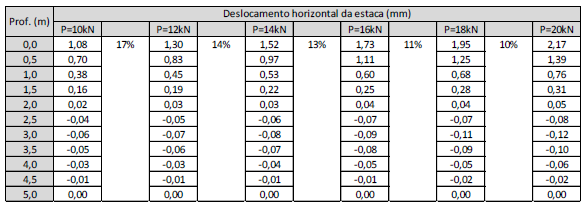
Figura 3. Funções de deslocamento das estacas – Análise paramétrica (Winkler)
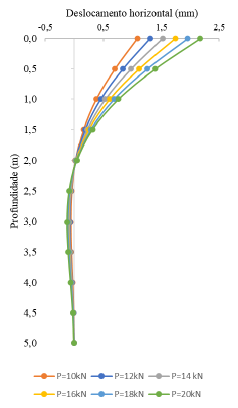
Conclui-se que ao aumentar os valores das cargas aplicadas, os deslocamentos máximos (no topo) também aumentam, conforme esperado. Vale ressaltar que o método de Winkler é baseado na Teoria da Elasticidade, porém para grandes deslocamentos haverá plastificação do solo ao redor da estaca. Portanto, espera-se que com um aumento de carga mais considerável, os deslocamentos sejam maiores e o perfil de deslocamentos se afaste do encontrado pela instrumentação, uma vez que a condição atingida se distancia do regime elástico.
2.3 Modelo de Pasternak modificado
O modelo proposto considera a interação entre as molas, do modelo de Winkler, e a resistência ao cisalhamento entre elas, através da variação, ou não, do módulo de cisalhamento do solo.
As hipóteses básicas do modelo são as seguintes:
(a) na direção longitudinal, a estaca é considerada como um feixe retangular, com largura de D e rigidez de EpIp;
(b) a força de cisalhamento pode ser transferida entre molas, e a camada de cisalhamento produz somente deslocamento de cisalhamento (direção y);
(c) a estaca está em contato o solo circundante e os deslocamentos da estaca são iguais aos deslocamentos na superfície de contato estaca-solo;
(d) existe o atrito apenas no sentido y, e o atrito lateral entre o solo e a estaca não é considerado.
A equação diferencial do modelo de Pasternak é dada por:

Onde,
G – módulo de cisalhamento do solo;
K – módulo de reação horizontal do solo;
EpIp – rigidez da estaca;
y – deflexão da estaca ao longo da profundidade z.
Considerando uma estaca livre no topo, as condições de contorno são:
i) No topo da estaca, z = 0;


Substituindo os parâmetros adotados nesse trabalho na equação (2.7), obtemos:

Realizando a variação de parâmetros na equação homogênea (2.12) com r = y’obtemos a seguinte equação característica:

Cujos os resultados são as raízes complexas apresentadas abaixo.
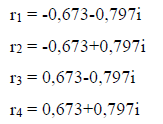
Desse modo, temos que:


Considerando as equações (4.2), (4.3), (4.4) e (4.5), pode-se montar o seguinte sistema de equações
para descobrir os valores das constantes C1, C2, C3 e C4.

Em sistemas de EDOs lineares com coeficientes constantes, pode-se fazer a resolução a partir da
redução da matriz a forma triangular, o sistema inicial (1) pode ser representado na forma abaixo.

A seguir é feito o cálculo dos quocientes q21, q31 e q41.
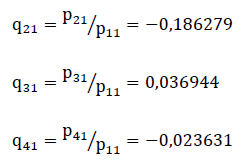
Com os valores de qi1 definidos, é realizado o seguinte processo para criação do sistema (2):
i) Multiplica-se a 1ª equação do sistema (1) por (-q21) e é adicionado o resultado à 2ª equação do sistema (1), isso resultará na 1ª equação do sistema (2);
ii) Multiplica-se a 1ª equação do sistema (1) por (-q31) e é adicionado o resultado à 3ª equação do sistema (1), isso resultará na 2ª equação do sistema (2);
iii) Multiplica-se a 1ª equação do sistema (1) por (-q41) e é adicionado o resultado à 4ª equação do sistema (1), isso resultará na 3ª equação do sistema (2);
iv) A 4ª equação do sistema (2) é a 1ª equação do sistema (1).
Resultando no sistema (2) apresentado abaixo em forma matricial.

Com os valores de qi2 definidos, é realizado o seguinte processo para criação do sistema (3):
i) Multiplica-se a 1ª equação do sistema (2) por (-q22) e é adicionado o resultado à 2ª equação do sistema (2), isso resultará na 1ª equação do sistema (3);
ii) Multiplica-se a 1ª equação do sistema (2) por (-q32) e é adicionado o resultado à 3ª equação do sistema (2), isso resultará na 2ª equação do sistema (3);
iii) A 3ª equação do sistema (3) é a 1ª equação do sistema (2).
iv) A 4ª equação do sistema (3) é a 4ª equação do sistema (2).
Resultando no sistema (3) apresentado abaixo em forma matricial.

Com os valores de q33 definidos, é realizado o seguinte processo para criação do sistema (3):
i) Multiplica-se a 1ª equação do sistema (2) por (-q22) e é adicionado o resultado à 2ª equação do sistema (2), isso resultará na 1ª equação do sistema (3);
ii) A 2ª equação do sistema (4) é a 1ª equação do sistema (3);
iii) A 3ª equação do sistema (4) é a 3ª equação do sistema (3);
iv) A 4ª equação do sistema (4) é a 4ª equação do sistema (3).
Resultando no sistema (4) apresentado abaixo em forma matricial.

A partir do sistema (4) podemos definir C4, e consequentemente os outros valores.
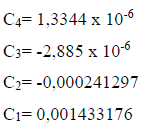
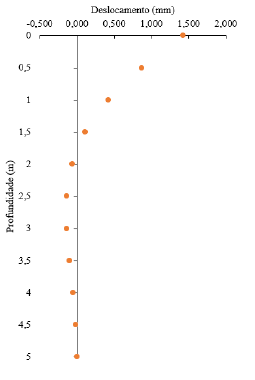
Dessa forma, substituindo os valores das constantes na função de deslocamento y(z), podem-se obter os valores de deslocamentos ao longo do comprimento da estaca, apresentados abaixo na Tabela 3 a cada 0,50 m, resultando também no Figura 4.
Tabela 3. Valores de deslocamento ao longo do comprimento da estaca
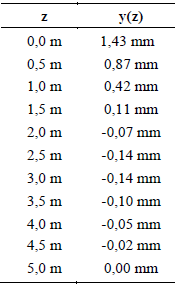
Figura 4. Função de deslocamento da estaca – Pasternak
2.3.1 Análise paramétrica – variação do diâmetro da estaca
Com o intuito de avaliar o impacto de alguns parâmetros de entrada na solução do problema, foi feita uma análise paramétrica variando o diâmetro da estaca. O diâmetro da estaca influencia diretamente na inércia da estaca, alterando a parcela correspondente à rigidez da estaca (EPIP). A mudança dessa parcela, acarreta na modificação do primeiro termo da Equação (2.13), resultando valores diferentes para as raízes complexas, e assim, também para as derivadas e sistema de EDO.
Toda a resolução abordada acima foi planificada, com as raízes da equação de 4° grau variando de acordo com a mudança em seu primeiro termo, foi feito o cálculo com diâmetros de 60 cm, 50 cm, 40 cm, 30 cm e 20 cm. Os resultados encontrados para os valores de deslocamento da estaca estão expostos na tabela e gráfico abaixo.
Tabela 4. Valores de deslocamento ao longo do comprimento de estacas com diferentes diâmetros
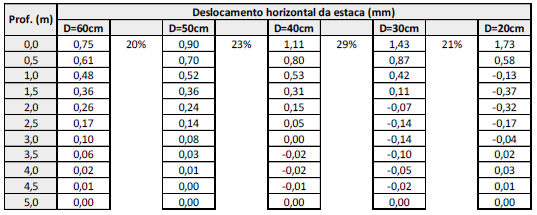
Figura 5. Funções de deslocamento das estacas – Análise paramétrica (Pasternak)
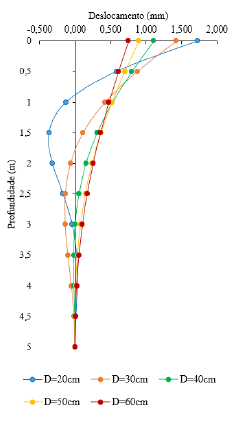
Nota-se que o aumento do deslocamento no topo da estaca fica em torno de 20% com cada aumento de 10 cm no diâmetro, mas como pode ser observado no gráfico acima, o diâmetro da estaca também influencia na forma da função deslocamento e não apenas nos valores.
Como esperado, estacas com maiores diâmetros, logo maior rigidez, sofrem menores deslocamentos na superfície e possuem uma função deslocamento mais retilínea que estacas com menores diâmetros. Estas, são mais esbeltas e com menor rigidez, tendendo a terem maiores deslocamentos, como foi observado.
4 Resultados de campo
O presente trabalho se baseou em uma situação real de provas de carga estática horizontal em uma estaca escavada isolada. Um inclinômetro foi instalado no interior da estaca, a fim de coletar os valores dos deslocamentos horizontais. Os ensaios foram realizados no Campo Experimental de Mecânica dos Solos da Unicamp, no qual o subsolo é caracterizado como silto-arenoso. Os resultados da instrumentação encontram-se na Figura 6.
Figura 6. Dados de deslocamento do inclinômetro
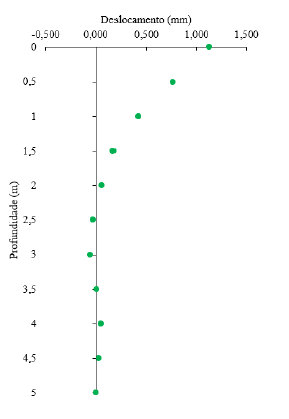
Através de uma rápida análise é possível notar que os dados do inclinômetro estão na mesma faixa de valores encontrados através das resoluções matemáticas, no item a seguir essa comparação poderá ser mais explorada.
5 Comparação entre resultados
Além das diferentes abordagens para o problema realizadas nos itens anteriores, foi utilizado o software SAP 2000 para o desenvolvimento de um modelo com as mesmas características do problema analisado. Através desse software, obtemos diferentes resultados para os deslocamentos da estaca, a cada 0,5 m, apresentados no gráfico abaixo.
Figura 7. Perfil de deslocamentos através do software SAP
A curva resultante dessa análise é semelhante às apresentadas para estacas com diâmetro de 30 cm e carga horizontal aplicada de 14 kN. Através dos resultados obtidos nas abordagens propostas no presente trabalho, pode-se realizar a comparação entre elas, que é apresentada pelo gráfico a seguir.
Figura 8. Comparação dos deslocamentos obtidos através de diferentes abordagens (P=14kN).
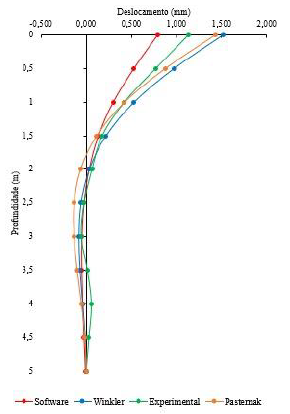
Observa-se que, de modo geral, houve uma convergência de valores teóricos e experimentais. Os métodos analíticos apresentaram valores de deslocamentos superiores quando comparados com os ensaios executados, sendo, portanto, a favor da segurança. A modelagem com o auxílio do software SAP 2000 apresentou deslocamentos inferiores quando comparados à instrumentação, mostrando, assim, uma análise contra a segurança.
6 Considerações Finais
A partir dos resultados obtidos e para os valores estudados (P=14kN e D=30cm), observa-se que embora o método de Pasternak considere o módulo de cisalhamento G, os deslocamentos não são afetados consideravelmente se comparados com a abordagem de Winkler, o qual não leva em consideração esse parâmetro.
Além disso, verifica-se que a rigidez da estaca (e, portanto, o diâmetro) está relacionada aos deslocamentos horizontais. A variação do diâmetro é mais sensível, nesse caso, do que a variação da carga.
Também se observou que os deslocamentos horizontais obtidos pelo SAP 2000 foram inferiores aos dados observados em campo (contra a segurança). Quanto às soluções analíticas, os resultados apresentaram valores semelhantes entre si e aos obtidos experimentalmente. Cabe lembrar que as diferenças relatadas são ínfimas (décimos de milímetros), o que nos permite dizer que são praticamente iguais quando tratamos de problemas relacionados à Engenharia Civil. Para maiores valores de carga, as quais poderiam fazer com que o solo ultrapasse o patamar elástico, as discrepâncias poderiam ser maiores e os métodos não são aplicáveis, pois eles se baseiam na teoria da Elasticidade.
Referências Bibliográficas
AOKI, N., VELLOSO, D. A. An aproximate method to estimate the bearing capacity of piles. In: Congreso Panamericano de Mecanica de Suelos y Cimentaciones. PASSMFE, 5., Buenos Aires. Anais… Buenos Aires: Sociedad Argentina de Mécanica de Suelos e Ingenieria de Fundaciones, p.367-376, 1975.
MARZOLA, M. M. Análise do comportamento de estaca escavada de pequeno diâmetro submetida a carregamento horizontal em solo não saturado. Dissertação de M. Sc., FEC/UNICAMP, São Paulo, SP, Brasil, 2016.
PASTERNAK, P. On a new method of an elastic foundation by means of two foundation constants. Gosudarstvennoe Izdatelstvo Literaturi po Stroitelstuve i Arkhitekture, 1954.
ROSENDO, D. C. Análise experimental e teórica de grupos de estacas carregadas horizontalmente em solo laterítico. Tese de D. Sc., FEC/UNICAMP, São Paulo, SP, Brasil, 2020.
SPIEGEL, M. R., LIPSCHUTZ, S., LIU, J. Mathematical handbook of formulas and tables. 3th Ed. McGraw Hills, 2009.
WINKLER, E. Theory of elasticity and strength. Prague, Czechoslovakia, 1867.
