COMPARATIVE ANALYSIS OF NEURAL NETWORKS IN PREDICTING TERRESTRIAL DIGITAL TELEVISION SIGNAL INTENSITY IN THE UHF BAND
REGISTRO DOI: 10.5281/zenodo.10276932
Alisson de Carvalho Souto1
Dr. Gilberto Arantes Carrijo2
Dr. Antônio Cláudio Paschoarelli Veiga2
Dr. Alexandre Coutinho Mateus2
Resumo
Esta pesquisa apresenta uma análise comparativa de Redes Neurais Artificiais baseada em algoritmos preditores para estimar a intensidade de campo elétrico em sinais de televisão digital terrestre. Os algoritmos de Levemberg-Marquardt, Regularização Bayesiana e Gradiente Conjugado Escalado tiveram seus resultados avaliados pelo Coeficiente de Correlação (R) e Mean Squared Error (MSE), quanto mais próximo de 1 o R e menor o MSE, melhores os resultados. O conjunto de 1.200 amostras medidas em campo foi dividido aleatoriamente em 80% para o treinamento, 10% para validação e 10% para os testes. Os três modelos ofereceram elevada precisão, sendo que o algoritmo de Regularização Bayesiana apresentou os melhores indicadores estatísticos, tanto no seu maior valor de regressão R quanto no menor MSE, em comparação com os algoritmos de Levemberg-Marquardt e Gradiente Conjugado Escalado, respectivamente.
Palavras chave: Televisão Digital Terrestre; Redes Neurais Artificiais; Levemberg-Marquardt; Regularização Bayesiana e Gradiente Conjugado Escalado.
Abstract
This study presents a comparative analysis of Artificial Neural Networks based on predictive algorithms to estimate the electric field strength in digital terrestrial television signals. The Levemberg-Marquardt, Bayesian Regularization and Scaled Conjugate Gradient algorithms had their results evaluated by the Correlation Coefficient (R) and Mean Squared Error (MSE), the closer to 1 the R and the lower the MSE, better the results. The set of 1.200 samples measured in the field was randomly divided into 80% for training, 10% for validation and 10% for testing. The three models provided high precision, and the Bayesian Regularization algorithm presented the best statistical indicators, both in its highest R regression value and in the lowest MSE, compared to the algorithms of Levemberg-Marquardt e Scaled Conjugate Gradient, respectively.
Key Words: Digital Terrestrial Television; Artificial Neural Networks; Levemberg-Marquardt; Bayesian Regularization; Scaled Conjugate Gradient.
1 INTRODUÇÃO
O espectro de frequências destinado à radiodifusão brasileira é um recurso limitado, o que impõe ao planejamento e gerenciamento de frequências situações constantemente desafiadoras para que seu compartilhamento se mantenha em coordenado. A predição automatizada de intensidade de sinais por modelos de propagação oferece meios apropriados ao projetista para a devida análise sobre o comportamento do sinal a ser irradiado, ao antecipar sua disponibilidade de cobertura e a possibilidade de convivência com as demais estações. A cobertura da rede e a prestação de serviços de qualidade são de suma importância no processo de planejamento da rede. Portanto, o conhecimento prévio do nível de intensidade de sinal é necessário para determinar se as características de propagação de rádio estão dentro os limites de uma determinada área de serviço. Complementarmente, tal conhecimento permite eventual redução em deslocamentos de equipes que vão a campo, maior segurança operacional aos profissionais de escritório e maior agilidade no atendimento de telespectadores, seja para confirmar previamente se possuem disponibilidade de sinal ou para apontar opções de menor custo de aquisição em sistemas de recepção, dispensando a necessidade de comparecimento às suas residências.
As Redes Neurais Artificiais (RNA) podem oferecer elevada assertividade em comparação aos tradicionais programas que utilizam os métodos de curvas de propagação teórico em uma solução alternativa de menor custo computacional, contanto que tais redes possuam uma base de dados consistente para seu adequado treinamento.
2 FUNDAMENTAÇÃO TEÓRICA
Os estudos acadêmicos que introduziram as Redes Neurais Artificiais como uma alternativa às previsões teóricas de intensidade de sinais de radiofrequência tiveram suas primeiras referências publicadas no final do século XX e, desde então, inúmeros estudos vem corroborando sua versatilidade.
Neskovic et al. (2002)publicaram um estudo no qualuma extensa quantidade de dados de medições de campo na frequência de 900 MHz da telefonia móvel celular foi incluída em uma rede projetada do tipo Multilayer Perceptron (MLP), a qual permitiu a comparação entre os dados obtidos e o modelo de previsão teórico em macrocélulas. Foram utilizados conjuntos de medições independentes que demonstraram que o modelo proposto apresentou precisão satisfatória para uso no planejamento de sistemas de rádio. Cerri et al. (2004) propuseram um método baseado neste mesmo tipo de RNA para previsão de perda de propagação de radiofrequência em áreas urbanas, apropriado para aplicações em planejamento de redes móveis celulares. Os resultados demonstraram tanto melhores resultados aos tradicionais métodos analíticos, quanto menor esforço computacional, em razão do paralelismo inerente à arquitetura das redes neurais.
Ostlin, Zepernik e Suzuki (2010) avaliaram uma RNA para a previsão de perda de propagação em uma macrocélula utilizando medidas coletadas em uma rede comercial CDMA (Code Division Multiple Access). Adicionalmente, foram utilizados diferentes algoritmos de retropropagação para treinamento, com destaque para o de Levenberg-Marquardt com parada antecipada, isto é, quando encontrada a convergência para um ponto ótimo. As entradas da rede foram escolhidas dentre parâmetros como a distância ao transmissor, perfil do terreno proveniente de perfis de mapas, tipo de vegetação e densidade predial nas proximidades da antena de recepção. Os resultados foram comparados com a recomendação ITU-R P.1546.1 e o modelo de Okomura-Hata. A RNA projetada trouxe um desempenho satisfatório, mesmo quando um simples modelo de neurônio foi empregado, acompanhada de baixa complexidade de processamento computacional.
Outro modelo empírico de RNA foi proposto por Angeles e Dadios (2015) para a previsão de perda de percurso em macrocélulas na área de radiodifusão, no qual as coletas de medidas de intensidade de campo de televisão digital terrestre obtidas na prática foram substituídas por resultados de uma simulação do modelo de Longley-Rice. Na sequência, tais dados foram usados para gerar o treinamento e validação da rede neural que, reajustada a retropropagação, o modelo de propagação baseado em rede neural agregou mais precisão aos resultados do que alguns convencionais modelos de propagação, como o Espaço Livre e Egli.
Ogbeide e Eko (2016) apresentaram uma rede neural avaliada e treinada com dados obtidos experimentalmente para predição de perda de caminho de propagação de sinal nas faixas de VHF (Very High Frequency) e UHF (Ultra High Frequency), utilizando três estações de radiodifusão em frequências distintas. Uma rede neural de duas camadas, uma camada oculta e uma camada de saída, foi avaliada quanto à sua precisão e propriedades de generalização. Os resultados de previsão de perda de caminho obtidos empregando o modelo de rede neural artificial foram avaliados em relação aos métodos empíricos de Hata e Walfisch-Ikegami. Os resultados da rede neural artificial na estimativa de perda de caminho foram apropriados para a previsão de sinal em comparação com os modelos de Hata e Walfisch-Ikegami e em linha de visada direta.
Popoola et al. (2018) desenvolveram uma RNA para predições de perda de percurso em mobilidade, normalizando os dados de perfil do terreno (longitude, latitude, elevação, altitude e altura do nível do terreno) e suas distâncias para estimar seus valores correspondentes, baseados no algoritmo de Levenberg-Marquardt. Os resultados também foram superiores em termos de precisão e habilidade de generalização quando comparados com os modelos de Hata, COST 231, ECC-33 e Egli.
Diversos autores ampliaram o escopo de seus trabalhos ao estabelecerem comparações entre diferentes algoritmos de treinamento, sobretudo utilizando Levemberg-Marquardt, Bayesian Regularization e Scale Conjugated Gradient. Os autores Bataineh e Kaur (2018) publicaram um estudo comparativo de diferentes ajustes de curvas de algoritmos usando conjunto de dados habitacionais. Kirisci, Demir e Simsek (2021) realizaram uma análise comparativa de redes neurais no diagnóstico de doenças emergentes baseadas em Covid-19. Chi (2022) utilizou o mesmo comparativo destes algoritmos para obter uma previsão do nível médio local do mar. Dixit e Mittal (2022) verificaram o melhor desempenho para rastreamento do apontamento máximo em um sistema solar fotovoltaico. Fauzi et. al. (2022) estimaram a previsão de cobertura de uma rede celular móvel baseada em algoritmos de aprendizado de máquina supervisionado. Os resultados proporcionados por todos estes trabalhos obtiveram sucesso em suas proposições.
Baseado nas pesquisas bibliográficas mais atualizadas disponíveis sobre o padrão brasileiro de televisão digital terrestre ISDB-Tb (Integrated Services Digital Broadcasting Terrestrial), não foram encontrados estudos significativos na aplicação simultânea de técnicas diversificadas de Machine Learning sobre esta tecnologia, especialmente no exame de seu sinal digital em mobilidade. Considerando que a utilização de rede neural tipo autorregressiva não-linear possibilita agregar, simultaneamente, dados determinísticos e estatísticos como vantagem aos métodos clássicos de previsão de predição de intensidade de sinal, que muitas vezes diferem do modelo ideal, se faz conveniente explorar mais o assunto. Nesta pesquisa, diferentemente das anteriores, um comparativo entre algoritmos de treinamento foi realizado na área de radiodifusão de televisão digital terrestre.
3 METODOLOGIA
Estabelecida como premissa estimar o campo elétrico de TV digital esperado para um determinado conjunto amostral com precisão satisfatória através do uso das RNA, este estudo tem o objetivo de comparar os algoritmos de treinamento de Levemberg-Marquardt (LM), Bayesian Regularization (BR) e Scale Conjugated Gradient (SCG) em termos de capacidade preditiva.
Para verificar individualmente o desempenho de cada algoritmo, o coeficiente de correlação ‘R’ entre os dados reais e previstos é comparado via LM, BR e SCG para critérios de desempenho, paralelamente ao seu respectivo valor de MSE (Mean Square Error), que atua como uma referência auxiliar de performance da rede. O valor de regressão dado por R é o principal indicador de precisão da rede. Ao se obter uma associação idêntica entre os dados de entrada e de saída, seu valor será 1, ao passo que, não havendo qualquer associação, seu valor será 0. Complementarmente, o erro quadrático médio dado pelo MSE é a disparidade quadrática média entre resultados e objetivos. Caso este atinja um valor nulo, indica que não a rede não apresenta erro algum.
Tanto o R quanto o MSE são usados para avaliar o desempenho da RNA. Os valores R e MSE são obtidos a partir das seguintes equações (MAHMOODI, NADERI, 2016):
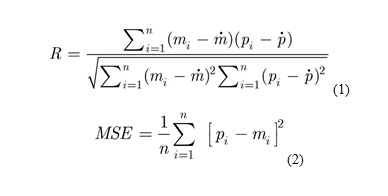
Onde mi representa os valores de dados experimentais, pi representa valores previstos e n é o número de amostras, ao passo que ṁ e ṗ são valores médios de m e p, respectivamente.
A Figura 1 apresenta o fluxo de elaboração do modelo paramétrico para predição do nível de recepção em análise nesta pesquisa.
Figura 1: Fluxo de elaboração do modelo de predição em análise
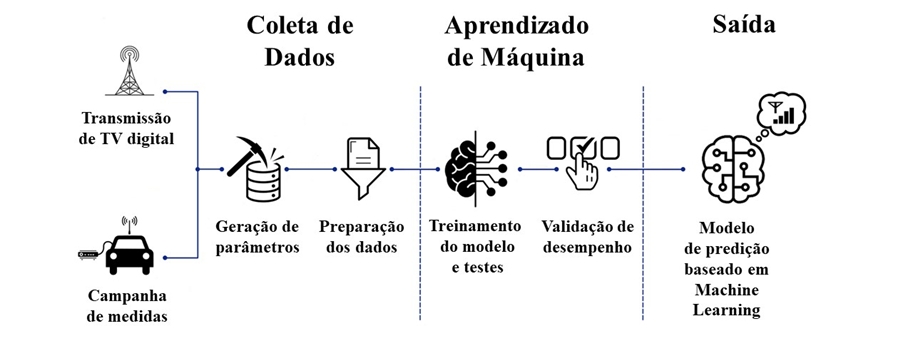
Fonte: Adaptado de Fauzi et. al. (2022)
O banco de dados para elaboração desta pesquisa foi originado a partir de medições de campo aferidas em Araguari, um município no interior do estado de Minas Gerais com cerca de 100.000 habitantes e altitude acima do nível do mar variando entre 940 e 1.087 metros.
Os sinais foram obtidos a partir de uma estação retransmissora de televisão com programação livre, aberta e gratuita, com potência enquadrada na Classe C, canal trinta digital, largura de banda de 6 MHz, frequência central de operação em 572 MHz na faixa de UHF (Ultra High Frequency) e antena de transmissão com polarização elíptica (70% horizontal; 30% vertical). A previsão de cobertura com intensidades de campo elétrico superiores a 51 dBµv da estação é indicada pela mancha digital, obtida a partir do método ponto-a-ponto e com o relevo digitalizado, gerada pelo programa EDX Signal Pro, da empresa EDX, empregando as curvas da Recomendação ITU-R P.1546-1, conforme ilustrado Figura 2. A campanha de medidas de campo em mobilidade foi realizada dentro da zona urbana da cidade, utilizando um medidor de intensidade de campo da Marca Anritsu, modelo Cellmaster MT8212E, acoplado a uma antena UHF do tipo monopolo vertical de meia onda, com 0 dB de ganho na recepção e cabo de perda desprezível. A base da antena foi disposta a uma altura de 1,5 metro do chão, acoplada magneticamente ao teto de um veículo de passeio, que cumpriu o percurso em velocidades inferiores a 40 km/h, com o intuito de minimizar os efeitos da perda por multipercurso. Foram coletados 1.458 pontos que registraram informações objetivas sobre as coordenadas geográficas (latitude e longitude, dadas em graus decimais), cota da base do ponto de recepção em relação ao nível do mar (em metros) e o nível de potência (em dBm) aferido para cada um dos pontos, conforme apresentado na Figura 2.
Figura 2: Mancha de cobertura sobreposta aos 1.458 pontos aferidos na cidade de Araguari
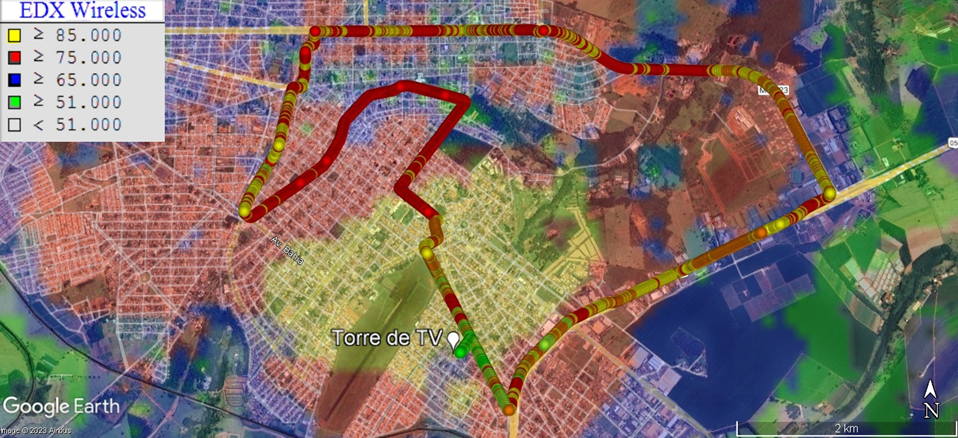
Fonte: Adaptado de Fauzi et. al. (2022)
Os dados do medidor de campo foram exportados no formato de arquivo KML (Keyhole Markup Language) e acessados no programa gratuito Google Earth, o qual permitiu complementar ao banco de dados, para cada ponto, informações de distância (em metros) e azimute de apontamento (em graus) relativos à antena transmissora. Com vistas a evitar valores atípicos, foram excluídos tanto os pontos em que o equipamento alertou saturação na recepção, quanto os pontos em que a distância à estação transmissora esteve inferior a 200 metros, restando 1.200 pontos efetivamente considerados neste estudo de caso.
Adicionalmente, de posse dos valores de distância e nível médio do terreno, os valores de intensidade de campo elétrico teórico foram calculados para cada um dos 1.200 pontos em análise e compuseram um novo parâmetro de entrada da rede neural, com base nas expressões da Recomendação ITU-R P.1546-1. Estipulada pela ANATEL – Agência Nacional de Telecomunicações para uso no Plano Básico de Distribuição de Canais de Televisão Digital (PBTVD), a primeira versão desta recomendação descreve os procedimentos para calcular a previsão de intensidade de campo para radiodifusão na faixa de frequências de 30 a 3.000 MHz, através da utilização de tabelas e curvas baseadas em análises estatísticas de dados empíricos. As curvas preveem os valores de intensidade de campo para uma potência irradiada efetiva de 1 kW, com valores de intensidade de campo excedidos em 50% do tempo. Nos casos em que as distâncias entre os pontos de análise e a altura da antena transmissora são diferentes dos valores lidos diretamente das curvas, a predição de campo deve ser obtida através de interpolação. A Figura 3 apresenta as curvas em percurso terrestre na faixa de 600 MHz.
Figura 3: Curvas experimentais utilizadas na Recomendação ITU-R P.1546-1
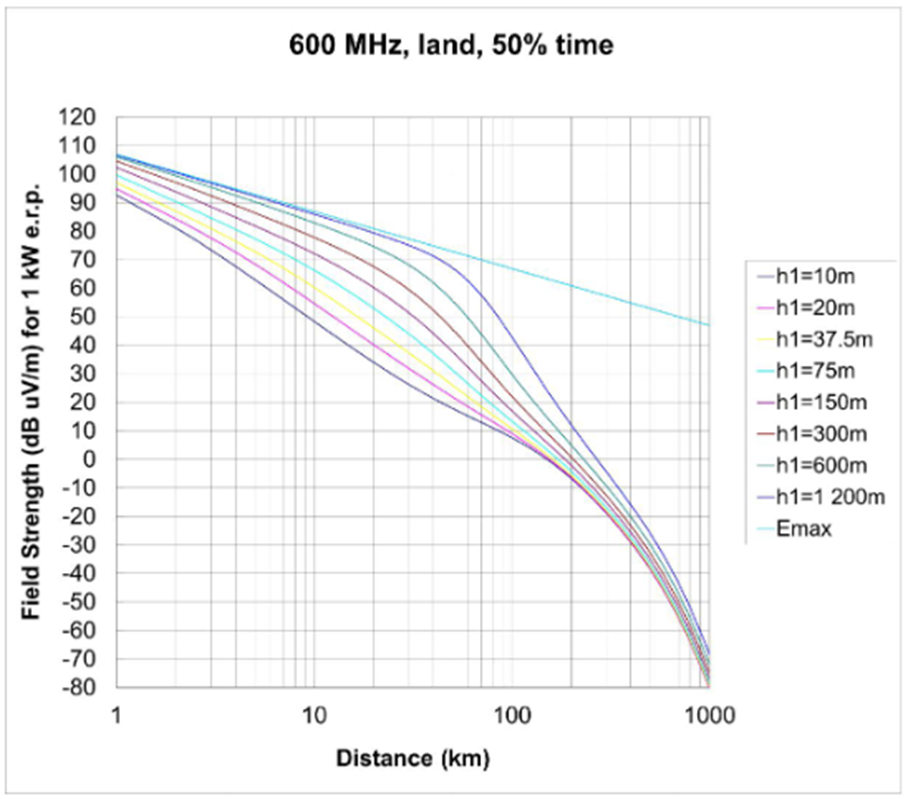
Fonte: União Internacional de Telecomunicações (2003)
Devido às diferenças físicas impostas por discrepâncias como o nível de precisão dos mapas cartográficos, a rugosidade das edificações provenientes da ação humana, do diagrama de irradiação da antena utilizada, entre outros, a intensidade de campo prevista para um determinado ambiente, com referência aos modelos empíricos existentes, muitas vezes difere do modelo ideal. Desse modo, houve a inclusão de uma sétima entrada, com vistas a reduzir o impacto destas diferenças mencionadas no valor ordinário alcançado pela norma. Baseado no Modelo de Perda de Propagação Log-Distância, que preceitua que a potência média do sinal recebido decresce logaritmicamente em função da distância, Rappaport (1996) propôs a inserção de um “Expoente de Perda para Diferentes Ambientes”, que sugere um valor de perda correspondente a obstáculos no entorno dos pontos de medição para complementar as informações de rugosidade do terreno não previstas nos modelos digitais de elevação topográfica.
A Tabela 1 apresenta valores típicos de ‘n’ para tais ambientes.
Ambiente Expoente de Perda de Propagação (n) Espaço Livre 2 Área Urbana 2,7 a 3,5 Área Urbana Sombreada 3 a 5 Obstruído por Edifícios 4 a 6 Obstruído por Fábricas 2 a 3
Tabela 1: Expoente de Perda para Diferentes Ambientes (RAPPAPORT, 1996)
Os referidos valores de expoente ‘n’ são combinados aos valores de potência do sinal medidos em campo, resultando na intensidade do sinal (em dBm) em um dado ponto de recepção, calculada pela Equação 3:
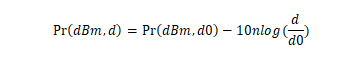
Onde Pr (dBm, d) é a intensidade do sinal em dBm no ponto de recepção, Pr (dBm, d0) é a intensidade do sinal em dBm no ponto de referência adquirido através de medição, d0 é a distância de referência próxima à antena de transmissão (neste estudo, foi considerada a distância de 200 metros), d é a distância que separa o transmissor do receptor e n é o expoente de perda de propagação, que indica a taxa com que a perda aumenta com a distância.
Os valores de potência referidos em dBm nesta pesquisa foram convertidas para dBµv, com vistas à uniformização das medidas. A unidade expressa em dBµV indica quanto menor ou maior é a tensão em relação a 1µV, com 0 dBµV correspondendo a 1 µV (microvolt).
Considerando a impedância característica (Z0) de 50 ohms, a fórmula utilizada é dada pela Equação 4.
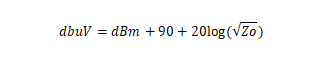
Os sete atributos de entrada da RNA foram submetidos à normalização pelo método de mínimos e máximos, com o objetivo de manter os valores de suas colunas numéricas dentro de uma escala comum, adequada à linguagem computacional e sem perda de informação. De acordo com AGGARWAL (2018), a fórmula de normalização aplicada é exibida na Equação 5:
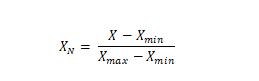
Onde X é o valor dos dados, Xmin é o valor mínimo em todo o conjunto de dados, Xmax é o valor máximo em todo o conjunto de dados e XN é o valor normalizado.
A REDE PROPOSTA
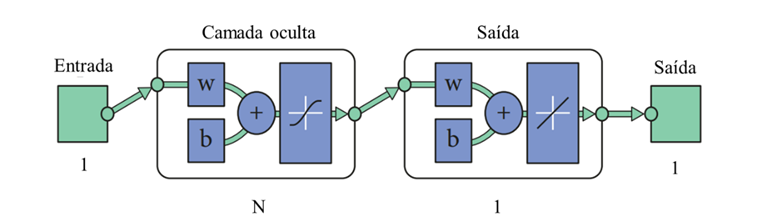
As RNA Backpropagation foram introduzidas na década de 1980 e seu algoritmo de retropropagação é um método de aprendizado supervisionado para redes feed-forward multicamadas, comumente aplicado às redes MLP. Tais redes de camadas múltiplas são estruturadas em pelo menos uma seção de entrada, uma seção de saída e outras camadas intermediárias entre entrada e saída, denominadas como camadas ocultas. A estrutura básica da RNA proposta é demonstrada na Figura 4, com função de transferência sigmóide na camada oculta e linear na camada de saída:
Figura 4: Estrutura Básica da RNA proposta
A rede MLP deste estudo foi idealizada para acomodar a complexa relação não-linear que ocorre nas variáveis em análise quando envolvidas em um ambiente urbano, incluindo suas edificações, vegetação, comércio e indústrias. Definir um modelo altamente preciso para estudos quantitativos depende de condições como a distribuição de parâmetros, o número de atributos de entrada e a complexidade das interações entre os preditores.
Cada um dos pontos de recepção (Rx) foi mapeado por suas características de azimute, distância em relação à estação transmissora, cota da base do nível do terreno, o nível de intensidade de campo elétrico predito pela norma e o nível de potência calculado no Expoente de Perda para Diferentes Ambientes, da Equação 3. Sua estrutura foi definida por uma única variável de saída que simula a correspondência do nível de recepção medido na prática, ou seja, um único vetor de valores atuou como alvo da RNA, conforme ilustrado na Figura 5:
Figura 5: Arquitetura do Modelo de RNA
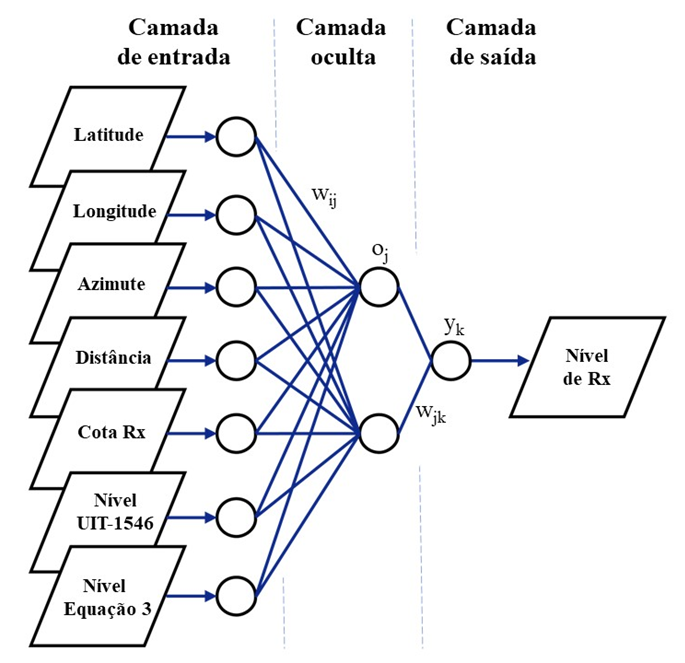
O banco de dados foi importado para a suíte de ferramentas de redes neurais disponível no programa de cálculo numérico Matlab R2022b, da empresa Mathworks, que oferece doze opções integradas de algoritmos de treinamento em RNA. Dentre as técnicas de regularização disponíveis na suíte Neural Net Fitting, LM e BR são capazes de obter erros quadráticos médios mais baixos do que qualquer outro algoritmo de treinamento, segundo Beale, e Demuth (2019). O algoritmo de gradiente conjugado escalonado foi escolhido como terceira opção deste comparativo por estar embarcado neste mesmo ambiente.
O algoritmo de Levenbreg-Marquardt (trainlm) é uma combinação dos métodos de minimização de Gauss-Newton e do gradiente descendente, usando a aproximação da segunda derivada sem a necessidade de se calcular uma matriz hessiana exata. Sua abordagem busca iterativamente o mínimo da função através da associação do vetor gradiente com a matriz Jacobiana. LM é o algoritmo que proporciona maior rapidez, às custas de um maior uso de memória computacional.
A regularização bayesiana (trainbr) minimiza a combinação linear de erros quadráticos e pesos. Apesar de exigir mais tempo de processamento do que LM ou SCG, este modelo de rede resiliente dispensa a necessidade de uma fase de validação, porque emprega um método próprio embarcado. O treinamento é interrompido quando cumpridas algumas das condições: o número máximo de épocas ou de tempo é atingido; o desempenho é minimizado para o destino; o desempenho do gradiente cai abaixo do parâmetro min_grad; ou quando excedido o parâmetro mu_max.
O algoritmo de gradiente conjugado escalonado (trainscg) é uma modificação da retropropagação e seu menor consumo de memória o destaca em relação aos demais do comparativo. Suas condições de parada são as supracitadas no BR, se distinguindo pela inobservância do parâmetro mu_max.
De um modo geral, o processo de treinamento dos algoritmos é interrompido automaticamente se não houver melhorias na generalização, guiado pelo aumento do erro quadrado médio das amostras de validação.
4 ANÁLISE DOS PARÂMETROS DA REDE
Determinar o modelo com melhor desempenho no comparativo entre LM, BR e SCG exige que o algoritmo seja treinado até a devida estabilização dos dados retornados. Para tanto, a definição do número de neurônios na camada oculta foi balizada pelo algoritmo de LM, referência na entrega de altos valores de correlação, modulando sistematicamente o número de neurônios até a rede convergir para a menor faixa possível de erros, tendo os mesmos parâmetros sido replicados aos demais algoritmos. A divisão do conjunto amostral obteve sua melhor conversão com 80% dos dados estabelecidos para o treinamento, 10% para os dados de validação e 10% para os dados de teste. Aleatoriamente, 1.200 amostras de dados foram divididas em 960 dados para treinamento, 120 dados para validação e 120 dados para teste.
Na avaliação do modelo proposto, os resultados obtidos demonstraram que a quantidade de 13 neurônios na camada oculta apresentou os menores valores de regressão R. A quantidade de iterações no processo de treinamento, nas quais ocorreram tentativas de minimizar a função de erro, superou 100 épocas nas avaliações dos três algoritmos.
As seções a seguir descrevem o comportamento de cada algoritmo, individualmente, conforme a obtenção de seus resultados.
4.1 Algoritmo de Levembertg-Marquardt
O melhor desempenho de validação na RNA empregando o algoritmo de LM foi época 110, conforme apresentado na Figura 6. Neste ponto foi criado um modelo otimizado com o mais baixo valor de MSE, situado em 2,3763, o que representa uma rede com baixo índice de erros. As linhas coloridas que compõem o gráfico simulam o treinamento, validação e teste e serão reproduzidas individualmente, nos três algoritmos deste comparativo. O processo é iniciado com o valor de MSE alto para evitar a ocorrência de sobreajuste e decresce seguindo o critério de validação. Após 110 épocas, o treinamento mantém o erro decrescente em função do tempo, porém os erros de validação e de teste passam a apresentar crescimento de forma simultânea, ao passo que o processo de treinamento é interrompido.
Figura 6: Resultado de Desempenho do algoritmo LM
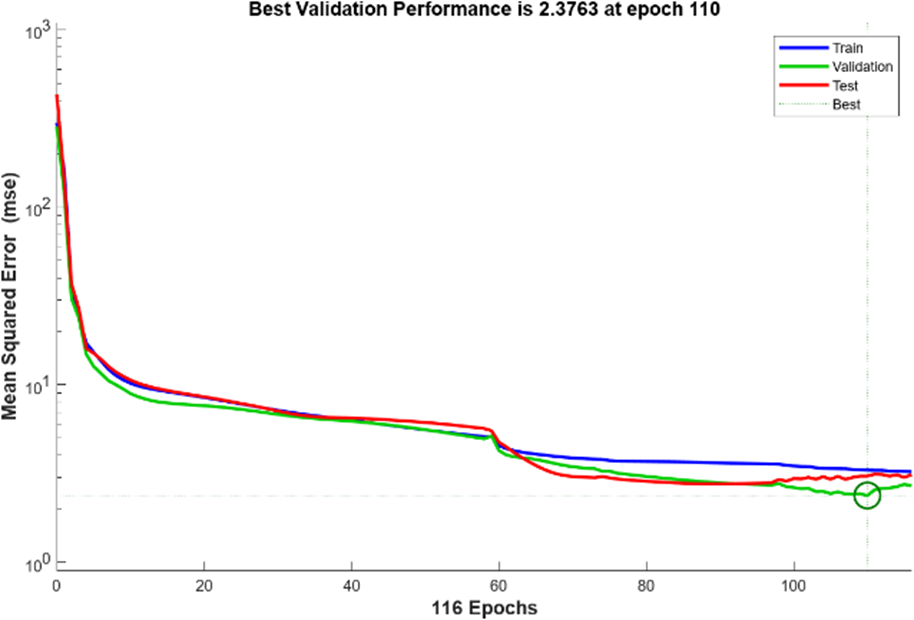
Os gráficos na Figura 7 apresentam os dados resultantes durante a regressão de treinamento, validação, teste e sua correlação geral de forma agrupada. A linha tracejada em cada gráfico observado nos diagramas de regressão simula as saídas com resultados perfeitos. A linha sólida em cada gráfico representa a linha de regressão linear mais adequada entre os resultados e os alvos. Os valores de regressão comprovaram a alta precisão de correlação do algoritmo de LM, superando o valor de 0,98 para todos os resultados deste algoritmo.
Figura 7: Gráfico de Regressão para o algoritmo LM
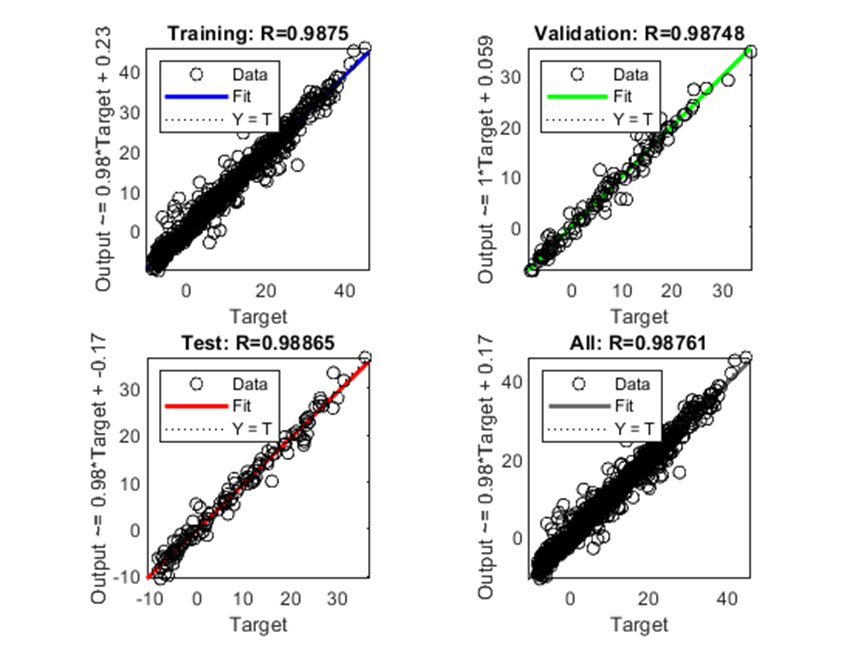
A Figura 8 representa o histograma de distribuição de erros do modelo para treinamento, validação e teste. As barras convergem para a linha central vermelha, as quais indicam zero erro no gráfico e o histograma de erros pode fornecer uma indicação acerca dos eventuais dados discrepantes. Uma distribuição equilibrada garante que o modelo seja treinado em um intervalo representativo do conjunto amostral. Caso a distribuição não seja equilibrada, mais dados semelhantes aos pontos discrepantes devem ser considerados na análise de treinamento e a rede deve ser treinada novamente. O gráfico exibido para LM apresenta uma distribuição predominantemente simétrica do erro e não possui dados discrepantes afetando a distribuição geral.
Figura 8: Histograma de erro para LM
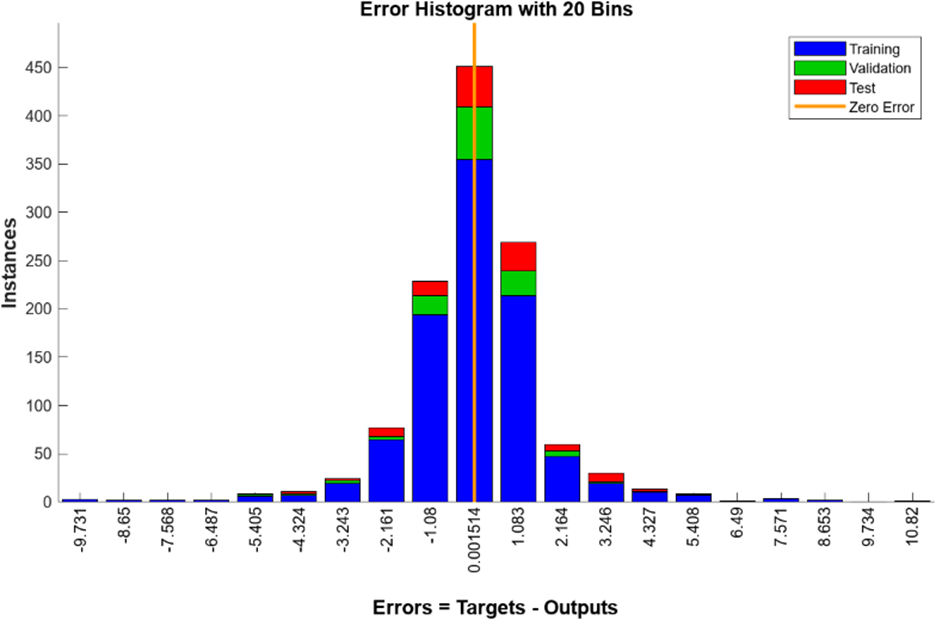
O treinamento baseado no algoritmo LM rendeu 98,7% de precisão para todas as amostras, 98,7% para treinamento, 98,7% para validação e 98,8% para testes, registrando uma alta correlação entre os valores reais e os valores alvo da rede.
4.2 Algoritmo de Regularização Bayesiana:
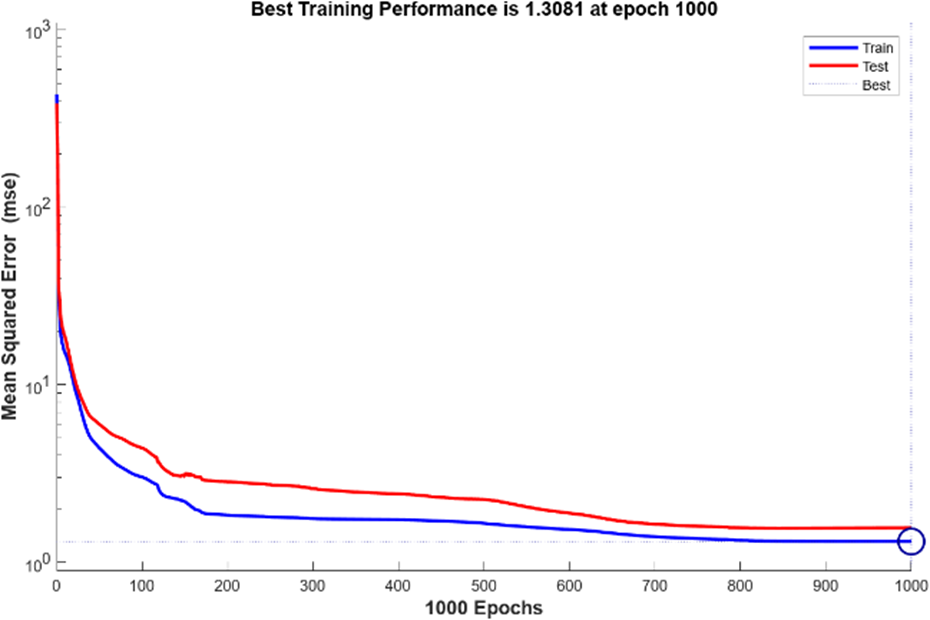
De modo similar à LM, o algoritmo de BR foi usado para treinar o modelo com o mesmo número de neurônios na camada oculta. A melhor performance no treinamento usando BR foi com o MSE de 1,3081 na época 1.000, tal como observado na Figura 9. Convém ratificar que este algoritmo possui um tipo de validação próprio durante a fase de treinamento.
Figura 9: Resultado de Desempenho do algoritmo BR
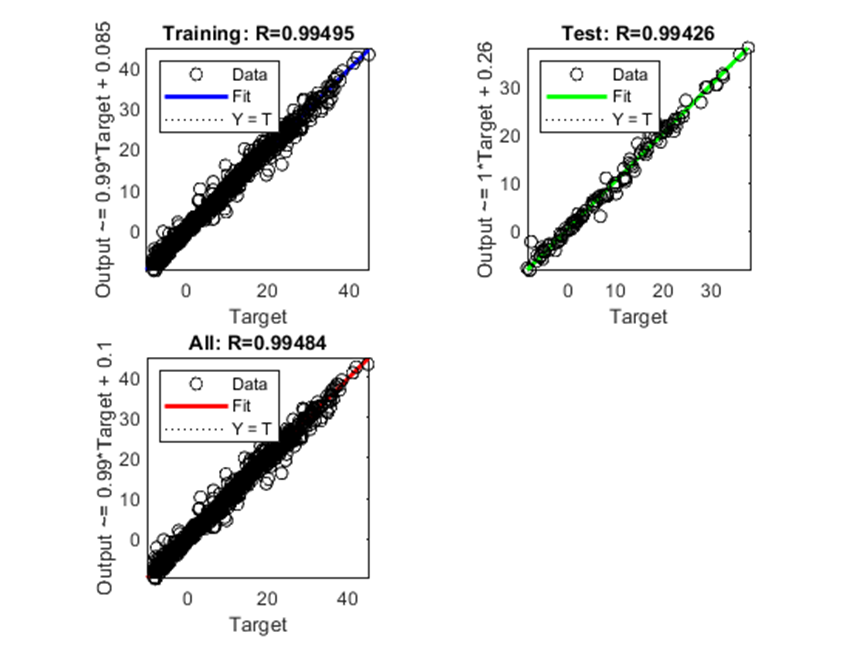
O parâmetro R em 0,99426 apresentou a mais alta correlação entre os valores de saída e os valores alvos do estudo proposto, conforme Figura 10.
Figura 10: Gráfico de Regressão para o algoritmo BR
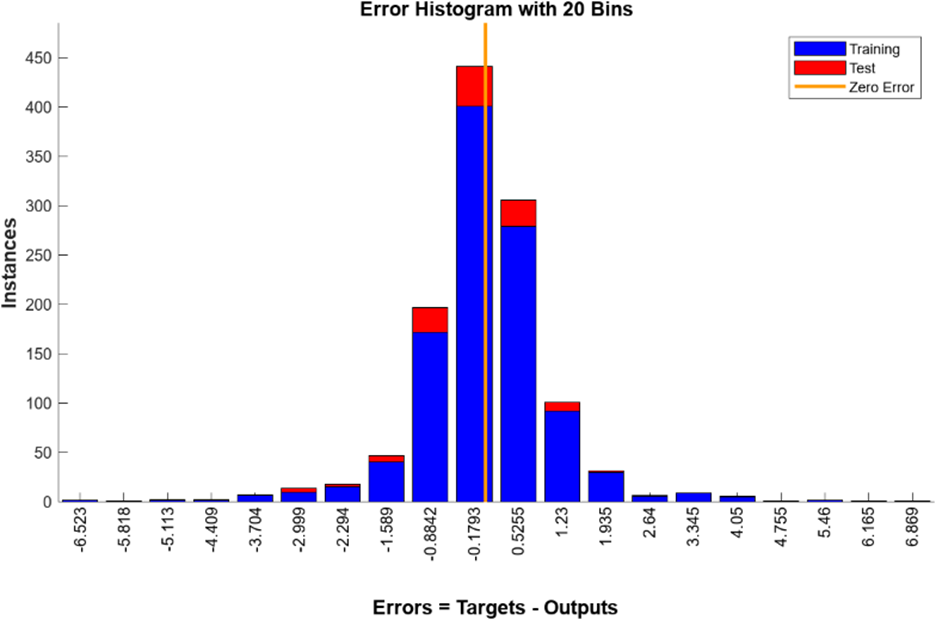
O histograma de erro apresentado na Figura 11 exibe uma distribuição balanceada de erros para treinamento, validação e teste, que mantém a generalização adequada da abordagem BR, com ocorrências ligeiramente maiores de frequências em valores negativos de erros em comparação com valores positivo.
Figura 11: Histograma de erro para BR
O treinamento baseado no algoritmo BR obteve 99,5% de acurácia para todas as amostras, 99,5% para treinamento e 99,4% para testes, ao passo que o MSE atingiu 1,5622. Tais valores se consolidaram nos melhores índices de precisão e acurácia encontrados neste comparativo.
4.3 Algoritmo de Gradiente Conjugado Escalonado:
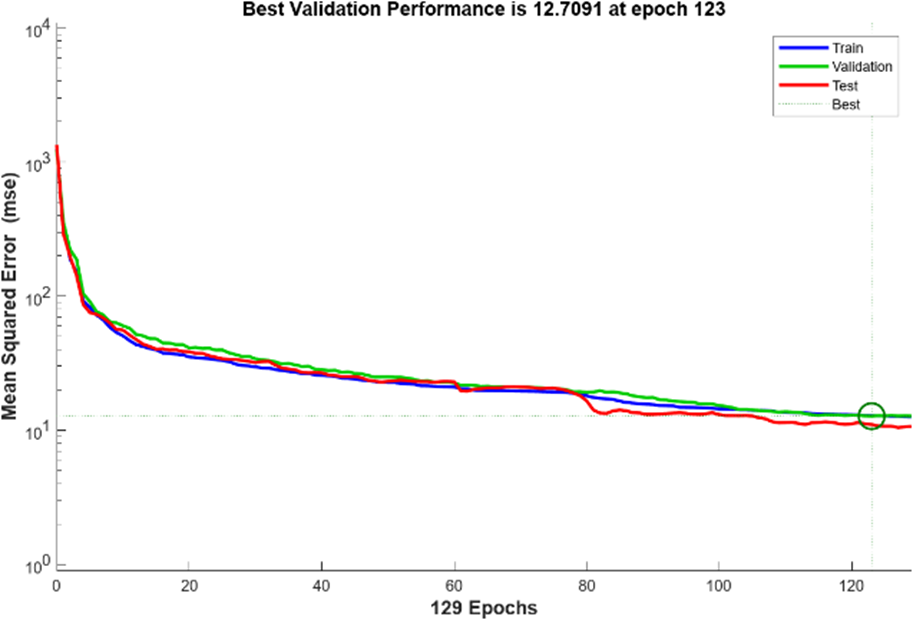
O algoritmo de SCG encerra seu treinamento automaticamente quando a generalização para de melhorar, conforme indicado por um aumento no erro quadrático médio das amostras de validação. O treinamento foi interrompido quando o erro de validação atingiu o máximo de seis verificações, previamente estipuladas como limite para este comparativo. O melhor desempenho de validação empregando o algoritmo de SCG foi 12,7091 na época 123. Apesar da Figura 12 exibir valores inferiores aos encontrados nos demais algoritmos, este valor de MSE ainda representa uma rede com alta qualidade para uso prático.
Figura 12: Resultado de Desempenho do algoritmo SCG
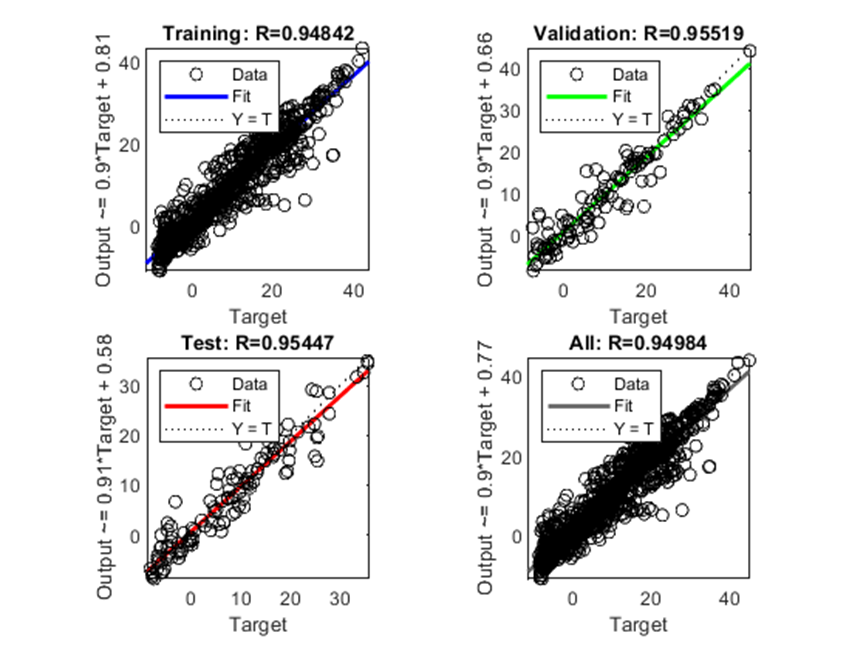
A Figura 13 demonstra o parâmetro R em 0,95447, que apresentou a menor correlação entre os valores de saída e os valores alvos do comparativo.
Figura 13: Gráfico de Regressão para o algoritmo SCG
O histograma de erro para SCG demonstra um comportamento semelhante ao observado em BR, no qual as frequências correspondentes a valores negativos de erros são relativamente maiores em comparação com as frequências correspondentes a valores positivos, conforme demonstrado na Figura 14.
Figura 14: Histograma de erro para SCG
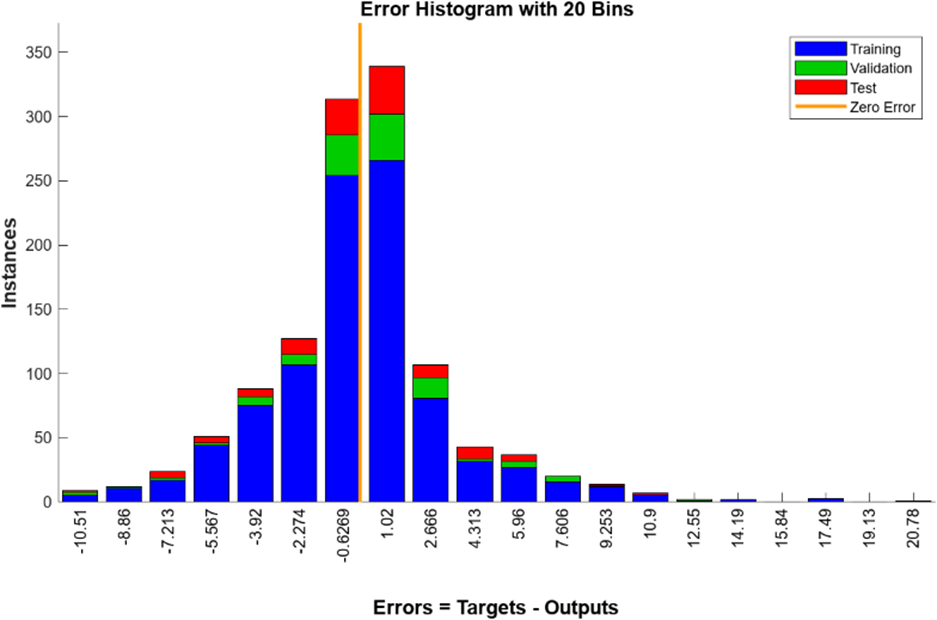
O treinamento baseado no algoritmo SCG rendeu 95% de precisão para todas as amostras, 94,8% para treinamento, 95,5% para validação e 95,4% para teste. O MSE atingiu 11,0061 durante os testes.
5 RESULTADOS E DISCUSSÕES
O objetivo deste estudo foi avaliar o desempenho dos algoritmos LM, BR e SCG para a previsão de intensidade de sinal de televisão digital e apontar o mais preciso destes modelos. Dado o espaço amostral em análise, foi possível obter um conjunto de resultados presumidamente aceitável para uma avaliação dos algoritmos.
A Tabela 2 apresenta o resumo geral das medidas de desempenho, com os resultados detalhados.
LM BR SCG Função no Matlab trainlm trainbr trainscg Número de Épocas 116 1.000 129 Desempenho 3,24 1,31 12,6 Gradiente 5,43 0,00611 9,52 MSE (Validação) 2,3763 – 12,7091 R (Validação) 0,9875 – 0,9552 MSE (Teste) 3,0580 1,5622 11,0061 R (Teste) 0,9886 0,9943 0,9545
Tabela 2: Resumo do comparativo de desempenho entre LM, BR e SCG
A premissa de se estimar o campo elétrico de TV digital com resultados satisfatórios através do uso das RNA foi plenamente atendida, com altos índices de precisão e acurácia. Os valores regressão demonstram uma associação quase idêntica entre os dados de entrada e de saída, ainda mais se notarmos a ordem de grandeza dos valores de saída, os quais foram escalonados em decibéis-microvolt. Paralelamente, os valores de disparidade quadrática média entre resultados e objetivos alcançados neste estudo correspondem a uma rede com baixa incidência de erros.
Os níveis de intensidade de campo obtidos a partir da mancha de cobertura e os valores calculados pela norma estiveram superiores aos colhidos na campanha de medidas, sobretudo se for levado em consideração que o relevo do município de Araguari é de uma topografia predominantemente plana. Por ser de médio porte, a cidade também não apresenta ruído urbano elevado. A RNA entregou valores muito mais próximos aos reais obtidos na prática do que os valores teóricos da mancha de cobertura e da norma técnica, os quais se mostraram muito otimistas para o caso em análise. Outro destaque para a RNA é sobre sua rápida velocidade de processamento e menor custo computacional, por dispensar as extensas interpolações envolvidas nos cálculos vetoriais do relevo digitalizado.
Considerando a proposta deste estudo, em obter com máxima precisão os valores de intensidade de campo elétrico na saída da RNA através da comparação dos algoritmos de treinamento, o algoritmo BR apresentou os melhores resultados deste comparativo em ambos os indicadores estatísticos avaliados. Em segundo lugar, o algoritmo de LM ofereceu resultados próximos, mas inferiores no que tange aos indicadores de Coeficiente de Correlação (R) e Mean Squared Error (MSE) e consumiu um tempo de processamento menor, respectivamente semelhante ao algoritmo SCG, que por sua vez inferiu a menor precisão deste comparativo. Tendo em vista o foco na qualidade entregue, o maior tempo de processamento computacional de BR em relação à LM e SCG pode ser considerado desprezível, sobretudo quando comparado aos programas específicos da área, com alto custo computacional.
Os resultados sugerem que as abordagens de redes neurais artificiais podem inferir com alta precisão o nível de intensidade de campo de televisão digital terrestre esperado em uma área, desde que tomadas de modo restrito, haja vista que estas simulações não podem extrapolar seu conjunto amostral.
6 CONCLUSÃO
A ampla variedade de preditores de entrada, composta pelas medidas de campo e pelo do aproveitamento de recursos gratuitos, materializou um banco de dados robusto, que permitiu à RNA entregar alta precisão nos resultados das simulações aliada a um baixo custo computacional. Por sua vez, a rede forneceu previsões para pontos de interesse diversos com exatidão maior do que as puramente trazidas pela norma ou pela mancha de cobertura teórica, as quais se mostraram muito otimistas em relação aos valores medidos na prática.
Empiricamente, os resultados revelaram que o algoritmo de treinamento BR foi o melhor do comparativo em sua alta performance de valor R e MSE baixo em relação algoritmos LM e SCG, classificados nesta ordem, sucessivamente. Não obstante, os testes evidenciaram que os três modelos analisados possuem valores de precisão comprovadamente aptos à utilização na prática.
Conclui-se que as Redes Neurais Artificiais podem oferecer uma alternativa de com elevada assertividade para a previsão de intensidade de sinal digital terrestre na faixa de UHF em comparação aos tradicionais programas computacionais específicos da área, desde possuam uma base de dados consistente para seu adequado treinamento.
As propostas de sugestões para trabalhos futuros estão relacionadas principalmente à próxima geração do Sistema Brasileiro de Televisão Digital Terrestre, denominada “TV 3.0”. Considerando o estipulado no Decreto nº 11.484, de 6 de abril de 2023, o novo padrão de TV digital manterá entre suas características a recepção em mobilidade. Consequentemente, este trabalho poderá contribuir para um eventual comparativo entre as características atuais e as provenientes da próxima tecnologia, prevista para iniciar as operações em meados de 2025.
7 BIBLIOGRAFIA
NESKOVIC, Aleksandar, et al. Macrocell Electric Field Strength Prediction Model Based Upon Artificial Neural Networks. IEEE Journal on Selected Areas in Communications, no. 06, 2002.
Disponível em: <https://ieeexplore.ieee.org/document/1021909> Acessado em 26 de abril de 2022. DOI: 10.1109/JSAC.2002.801217
CERRI, G.; CINALLI, M.; MICHETTI, F.; RUSSO, P. Feed forward neural networks for path loss prediction in urban environment. IEEE Transactions on Antennas and Propagation, Institute of Electrical and Electronics Engineers (IEEE), v. 52, n. 11, p. 3137–3139, nov. 2004. Disponível em: <https://doi.org/10.1109/tap.2004.835252>
ÖSTLIN, Erik; ZEPERNICK, Hans-Jürgen; SUZUKI, Hajime. Macrocell radio wave propagation prediction using an artificial neural network, IEEE 60th Vehicular Technology Conference, no. 06, 2004.
Disponível em: <https://ieeexplore.ieee.org/document/1399921> Acessado em 15 de maio de 2022. DOI: 10.1109/VETECF.2004.1399921
ANGELES, Joel C. Delos; DADIOS, Elmer P. Neural network-based path loss prediction for digital TV macrocells, International Conference on Humanoid, Nanotechnology, Information Technology, Communication and Control, Environment and Management (HNICEM), no. 15754126, 2015.
Disponível em: <https://ieeexplore.ieee.org/document/7393223> Acessado em 25 de outubro de 2022. DOI: 10.1109/HNICEM.2015.7393223
OGBEIDE, Kinglsey; EKO, Jimmy Ebi. Path-Loss Prediction for UHF/VHF Signal Propagation in Edo State: Neural Network Approach. APTIKOM Journal on Computer Science and Information Technologies, no 02, 2016.
Disponível em: <http://aptikomjournal.com/index.php/CSIT/article/view/113> Acessado em: 17 de novembro de 2022. DOI:10.11591/APTIKOM.J.CSIT.113
POPOOLA, Segund I., et al. Characterization of Path Loss in the VHF Band using Neural Network Modeling Technique. 19th International Conference on Computational Science and Its Applications (ICCSA), no. 19030447, 2019.
Disponível em: <https://ieeexplore.ieee.org/document/8853607> Acessado em 25 de outubro de 2022. DOI: 10.1109/ICCSA.2019.00017
BATAINEH, Ali Al; KAUR, Devinder. A Comparative Study of Different Curve Fitting Algorithms in Artificial Neural Network using Housing Dataset. NAECON 2018 – IEEE National Aerospace and Electronics Conference, no. 18293492, 2019.
Disponível em: <https://ieeexplore.ieee.org/document/8556738> Acessado em 17 de julho de 2023. DOI: 10.1109/NAECON.2018.8556738
KİRİSCİ, Murat; DEMİR, İbrahim; ŞİMŞEK, Necip. Comparative Analysis of Neural Networks in the Diagnosis of Emerging Diseases based on COVID-19. Konuralp Journal of Mathematics, no. 2, 2021.
Disponível em: <https://dergipark.org.tr/en/download/article-file/1960322> Acessado em 07 de julho de 2023.
CHI, Yeong Nain. Application of Nonlinear Autoregressive Neural Network Model to Forecast Local Mean Sea Level. Journal of Computing and Applied Informatics (JoCAI), no. 2, 2022. Disponível em: <https://talenta.usu.ac.id/JoCAI/article/view/8975> Acessado em 21 de dezembro de 2022. DOI: https://doi.org/10.32734/jocai.v6.i2-8975
DIXIT, Vashu; MITTAL, Preeti. A Comparative Analysis of ANN Algorithms Performance for Maximum Power Point Tracking in Solar Photovoltaic System. International Journal for Research in Applied Science & Engineering Technology (IJRASET), no. 2, 2022.
Disponível em: <https://doi.org/10.22214/ijraset.2022.46055> Acessado em 12 de julho de 2023.
FAUZI, Moud. F. A. Mobile Network Coverage Prediction Based on Supervised Machine Learning Algorithms. IEEE Access, no. 10, 2022.
Disponível em: https://ieeexplore.ieee.org/document/9779262 Acessado em 18 de julho de 2022. DOI: 10.1109/ACCESS.2022.3176619
ITU. Method for point-to-area predictions for terrestrial services in the frequency range 30 MHz to 4 000 MHz. [S.l.], 2019.
RAPPAPORT, Theodore. S. Wireless Communications Principles And Practice. 2. ed. New Jersey: Prentice Hall, 2002. 104 p.
AGGARWAL, Charu C. Neural Networks and Deep Learning A Textbook. Yorktown Heights: Springer International Publishing AG, 2018, 127 p.
DEMUTH, Howard; BEALE, Mark. Neural Network Toolbox User’s Guide Version 4; The Math Works Inc.: Natick, MA, USA, 2000; pp. 5-22.
MAHMOODI, Masoud; NADERI, Ali. Applicability of Artificial Neural Network and Nonlinear Regression to Predict Mechanical Properties of Equal Channel Angular Rolled Al5083 Sheets. Latin American Journal of Solids and Structures, no. 13, 2016.
Disponível em: <https://doi.org/10.1590/1679-78252154> Acessado em 20 de julho de 2023.
1Discente do Curso de Mestrado Científico em Engenharia Elétrica da Universidade Federal de Uberlândia.
2 Docentes da Faculdade de Engenharia Elétrica (FEELT/UFU)
