FUNDAMENTAL THEOREM OF ALGEBRA: AN INTELLIGIBLE DEMONSTRATION TO HIGH SCHOLL TEACHERS
REGISTRO DOI: 10.69849/revistaft/cs10202505311201
Carlos Kleber Alves do Nascimento
RESUMO
Este artigo tem o objetivo de contribuir na formação continuada de professores do Ensino Médio no sentido de permitir um melhor entendimento da demonstração do Teorema Fundamental da Álgebra (TFA) que afirma que todo polinômio não constante com coeficientes complexos possui pelo menos uma raiz complexa. Ademais, fornece uma percepção das tentativas históricas de demonstrá-lo. Inicialmente foram trabalhados alguns conceitos, definições e teoremas que auxiliam o entendimento dessa demonstração. Fazendo uso das noções básicas de topologia, cálculo diferencial e análise complexa, procurei detalhar a demonstração do TFA de modo que qualquer professor do Ensino Médio consiga entendê-lo.
Palavras-chave: Teorema Fundamental da Álgebra, demonstração, tentativas históricas.
ABSTRACT
This article aims to contribute to the continuing education of high school teachers in order to enable a better understanding of the statement of the Fundamental Theorem of Algebra (TFA) which states that every non-constant polynomial with complex coefficients has at least one complex root. Moreover, it provides a perception of historical attempts of prove it. Initially were worked out some concepts, definitions and theorems that help to understand this demonstration. Making use of the basics of topology, differential calculus and complex analysis, I tried to detail the demonstration of TFA so that any high school teacher can understand it.
Keywords: Fundamental Theorem of Algebra, demonstration, historical attempts.
1. INTRODUÇÃO
Tradicionalmente o Teorema Fundamental da Álgebra (TFA) é provado em cursos de uma variável complexa nos bacharelados de matemática e física e/ou nos cursos de pós-graduação em matemática e física, sendo que não raras vezes os alunos têm contato com tal teorema pela primeira vez na pós-graduação. Em tais cursos, geralmente o TFA é provado logo após o Teorema de Liouville, o qual é deduzido da Fórmula Integral de Cauchy, devida a A. L. Cauchy (1789-1857), que para sua prova requer o estudo da Teoria da Integração em uma Variável Complexa. Muitas vezes o TFA é demonstrado utilizando a Teoria de Galois ou a Topologia Algébrica, que são teorias sofisticadas. (OLIVEIRA, 2015,p. 8).
É fato que a explicação da prova do TFA na graduação por vezes é deixada de lado, sendo esse conhecimento pertencente apenas a um pequeno grupo do locus acadêmico. Dessa forma, este artigo tem o objetivo de auxiliar na formação do professor de Matemática do Ensino Médio no que diz respeito aos antecedentes históricos e a demonstração do TFA que afirma que todo um polinômio p(z) não constante com coeficientes complexos possui pelo menos uma raiz complexa.
No intuito de facilitar o entendimento desta demonstração, primeiramente recordamos que C constitui um corpo, vimos alguns conceitos e propriedades dos números complexos e em seguida foi dada uma interpretação geométrica para os elementos de C. Na quinta seção, introduzimos a noção de polinômios com coeficientes complexos e algumas definições e na sexta seção foram apresentadas noções topológicas elementares do plano complexo.
Ademais, fizemos uma retrospectiva histórica das principais tentativas de demonstrá-lo. Nesse contexto, é oportuno lembrar que segundo D’Ambrósio (1996):
Uma percepção da história da matemática é essencial em qualquer discussão sobre a matemática e o seu ensino. A história da matemática é um elemento fundamental para perceber como teorias e práticas matemáticas foram criadas, desenvolvidas e utilizadas num contexto específico de sua época. (D’AMBRÓSIO, 1996, p.29-30).
É claro que qualquer tentativa de demonstração do TFA para um aluno do Ensino Médio amparada apenas num corpus teórico formal tende ao fracasso, mas segundo (LIMA, 2006), é interessante que pelo menos o professor tenha uma ideia sobre como demonstrá-lo.
Na nona seção é apresentada algumas consequências do TFA como o fato de que se p(z) é um polinômio não nulo com coeficientes em C tem grau n, então p(z) tem no máximo n raízes em C e podemos escrever p(z) como produto de n fatores de grau 1.
2. O CORPO DOS NÚMEROS COMPLEXOS
Nesta seção, veremos que o conjunto R2 munido das operações de adição e multiplicação satisfaz uma série de propriedades que o qualifica como um corpo. Este corpo é usualmente denotado por C e os seus elementos são chamados de números complexos. Para tanto, baseamo-nos em (SOARES, 2007).
Dado o conjunto de todos os pares ordenados de números reais, podemos definir duas operações binárias – uma adição (denotada pelo símbolo +) e uma multiplicação (denotada pelo símbolo • ) – da seguinte maneira:
(x1, y1) + (x2,y2) = (x1 + x2, y1 + y2)
(x1, y1) (x2, y2) = (x1x2 – y1y2, y1x2 + x1y2)
Observe que a adição como foi definida é a adição usual do espaço vetorial R2 pelo que, como sabemos, goza da propriedade comutativa e associativa; além disso, (0,0) é o elemento neutro para esta operação e todo par (x,y) tem inverso (-x,-y) também chamado de simétrico. Quanto à multiplicação, facilmente se mostra que também é comutativa e associativa, que existe elemento neutro (ou identidade) para esta operação ( o par (1,0)) e que todo o elemento (x,y) ≠ (0,0) tem inverso, dado por
Finalmente, a multiplicação é distributiva em relação à adição.
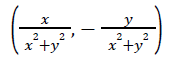
Exemplo: Mostre que a operação definida em C = R2 por
(x1, y1) . (x2, y2) = (x1x2 – y1y2, y1x2 + x1y2 )
é comutativa e satisfaz (1,0) ∙ (x,y) = (x, y), para todo (x,y) E R2.
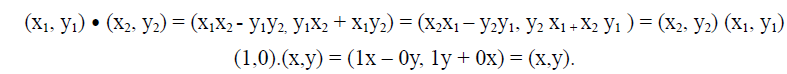
Exemplo: Mostre que a operação definida no exemplo anterior é tal que se (x,y) ≠ (0,0), então existe (u,v) E C tal que (x,y) ∙ (u,v) = (1,0).
Inverso Multiplicativo: Se (x,y) ≠ (0,0), então podemos definir
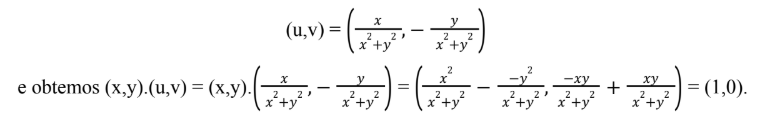
As propriedades mencionadas nos permitem, portanto, afirmar que o conjunto R2, munido das operações de adição e multiplicação definidas, constitui um corpo. Considere a aplicação:
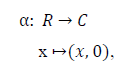
e note-se ainda que para quaisquer x,y E R, se tem
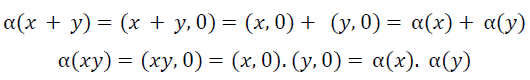
3. UNIDADE IMAGINÁRIA, FORMA ALGÉBRICA E PROPRIEDADES
Nesta seção serão apresentadas algumas informações relevantes à respeito dos números complexos como sua forma imaginária, forma algébrica e as principais propriedades que corroboram para o entendimento da demonstração do TFA. Para tanto, baseamo-nos em (SOARES, 2007) e (HEFEZ, 2012).
É usual denotar o complexo (0,1) pelo símbolo i. Utilizando esta notação e fazendo a identificação anterior dos complexos da forma (x,0) com os correspondentes números reais x, tem-se (x,y) = (x,0) + (0,y) = (x,0).(1,0) + (y,0).(0,1) = x.1 + y.i = x + yi.
Dessa forma, todo número complexo (x,y) pode também ser designado por x+ yi. Esta é a chamada forma algébrica de z, sendo esta a notação que passaremos a usar para 2 números complexos neste trabalho. É então imediato reconhecer que denotando por z2 o complexo z.z se tem i2 = i.i = (0,1) = -1. Dado um número complexo z = x + yi chamamos a x parte real de z e a y de parte imaginária de z, e escrevemos Re z := x e Im z := y. Com o auxílio da forma algébrica de um número complexo z e considerando os números complexos z e , podemos reescrever as operações z1 = x1 + y1i e z2 = x2 + y2i de adição e multiplicação em C da seguinte forma:
Adição: a soma z1 + z2 é obtida pelas somas das respectivas partes real e imaginária,
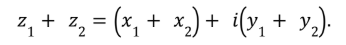
Multiplicação: aplicamos a distributividade e agrupamos a parte real e imaginária (lembrando que i2 =− 1) :
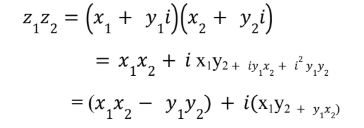

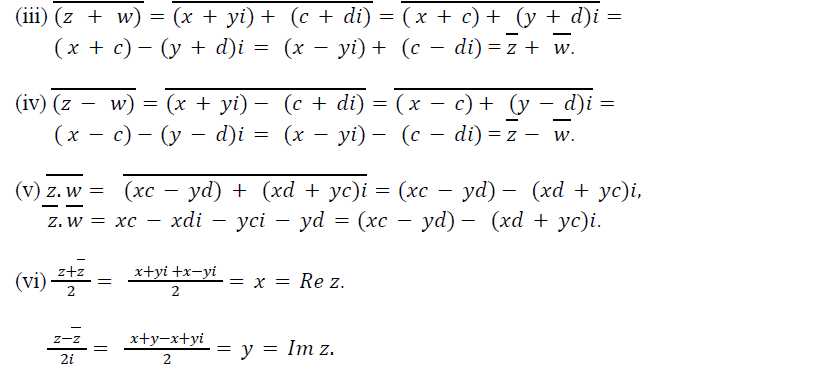


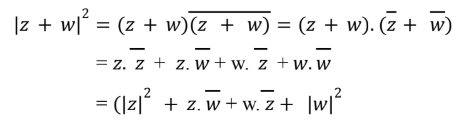
Temos pela proposição 1(v) e usando a proposição 2 que:
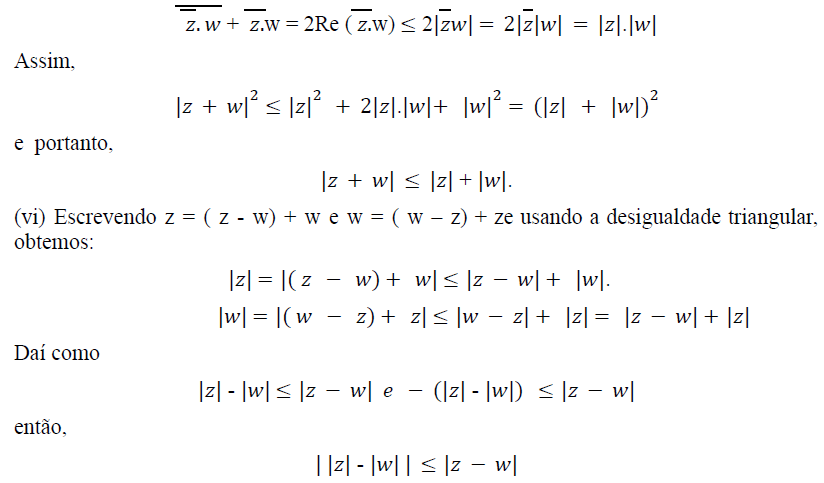
A outra desigualdade pode ser obtida fazendo as modificações convenientes acima.
4. PLANO COMPLEXO
Veremos agora como podemos dar uma interpretação geométrica para os números complexos. A seção foi baseada em (SOARES, 2007).
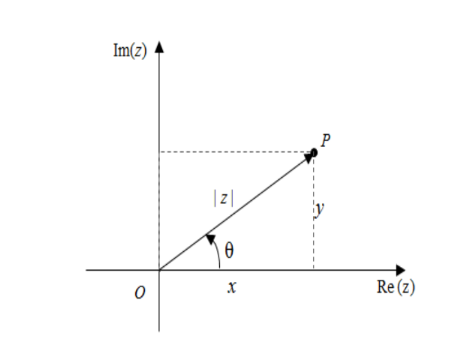
Fixado um sistema de coordenadas cartesianas num plano, a cada número complexo z = x+ yi poderá associar-se, de modo único, o ponto de coordenadas (x,y) = (Re z, Im z) desse plano ( ou se preferirmos, o vetor que une a origem de coordenadas a esse ponto). Estabelece-se, assim, uma bijeção entre o conjunto dos números complexos e o conjunto dos pontos desse plano. Os números reais ( ou seja, os complexos de parte imaginária nula) correspondem ao eixo das abscissas, o qual é designado por eixo real; de modo análogo, os complexos da forma iy ( isto é, os complexos de parte real nula)- chamados imaginários puros – correspondem ao eixo das ordenadas, o qual costuma ser designado por eixo imaginário. Quando o plano xy é utilizado, deste modo, para a representação de números complexos, é usual chamar-lhe plano complexo ou plano de Argand-Gauss. Muitas vezes, identificamos completamente o conjunto C com este plano e referimo-los a C como o plano complexo, falando no ponto z = x +yi.
5. POLINÔMIOS COM COEFICIENTES COMPLEXOS
Nesta seção, veremos a definição de polinômios com coeficientes em C, a definição de grau e mais algumas características envolvendo esses polinômios. A seção está baseada em (HEFEZ, 2012).
Um polinômio p(z) com coeficientes em C é uma expressão formal do tipo

No conjunto dos polinômios com coeficientes complexos, podemos definir as operações de adição e multiplicação de polinômios, a partir da operação de adição e multiplicação de C.
6 NOÇÕES TOPOLÓGICAS DO PLANO COMPLEXO
Veremos agora, algumas noções elementares sobre a topologia do plano complexo. Alguns desses conceitos são similares aos da reta real. Estas noções são baseadas na forma de medir a distância entre dois pontos do plano complexo. A seção está baseada em (TOFFOLI, 2004).
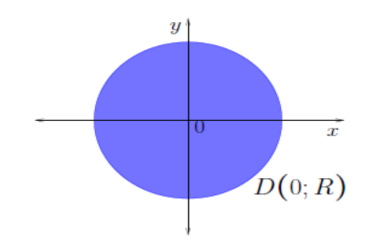
Disco aberto: Dados um real r > 0 e um número complexo arbitrário z0, definimos o disco aberto de centro z0 e raio r como o conjunto Dr(z0) de todos os números complexos que estão a uma distância menor do que r do ponto z0 isto é,
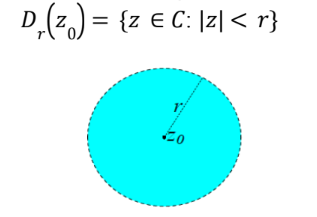
Fonte: (SOARES, 2007, p.36)
Disco fechado: Dados um real r > 0 e um número complexo arbitrário z0, definimos o disco fechado de centro z0 e raio r como o conjunto de todos os números Dr(z0)complexos que estão a uma distância igual ou menor do que r do ponto z0 isto é,

Fonte: (SOARES, 2007,p.36)

i é um ponto de acumulação de S e não pretence ao conjunto S.
Conjunto aberto: Um conjunto S é aberto, se o seu complementar Sc é um conjunto fechado.
Conjunto limitado: Um conjunto S é limitado, se existe uma constante M > 0 tal que |z| < M para todo z em S. Se o conjunto não é limitado, ele é dito ilimitado.
Conjunto compacto: Um conjunto S do plano é dito compacto, se é, ao mesmo tempo, um conjunto fechado e limitado.
Com o intuito de facilitar o entendimento do TFA, vejamos o que diz o lema abaixo cuja demonstração se encontra em (DELBONI, 2015).
Lema 1: Se p(z) é um polinômio não constante com coeficientes em C, então dado M > 0, existe um raio r > 0 tal que se |z| > r, então |p(z)|≥M.

7. ASPECTOS HISTÓRICOS DO TEOREMA FUNDAMENTAL DA ÁLGEBRA
A partir de agora discutiremos, sob um ponto de vista histórico, algumas tentativas de demonstrar o Teorema Fundamental da Álgebra (TFA) que afirma que todo polinômio com coeficientes em C de grau maior ou igual a 1 possui pelo menos uma raiz complexa. A seção foi baseada em (OLIVEIRA, 2015.p. 4-6).
Séculos antes da criação dos números complexos, François Vieta (1540-1603) exibiu várias equações (polinomiais com coeficientes reais) de grau n com n raízes. Peter Roth (falecido em 1617) já afirmou, em 1608, que equações polinomiais com coeficientes reais de grau n tem no máximo n raízes. Porém, Roth já utilizara que tais equações efetivamente admitem raízes. O matemático belga, nascido na França, Albert Girard (1595-1632), na sua “L’invention Nouvelle en l’Algèbre”, em 1629, foi o primeiro a afirmar que há sempre soluções (possivelmente repetidas) para tais equações, mas não demonstrou tal fato.
René Descartes (1596-1650), na terceira parte ” La Geométrie”, em 1637, descreve tudo o que se conhecia à época sobre equações polinomiais, observa que um polinômio p(x) com coeficientes reais na variável real x que se anula em um número real α é divisível pelo polinômio de grau um (x – α) e apresenta a famosa “regra dos sinais” para calcular o número máximo de raízes reais positivas e negativas.
O alemão G. W. Leibniz (1646-1716), procurando integrar uma função dada pela divisão de dois polinômios com coeficientes reais, na “Acta Eruditorum” de 1702 considera a questão de saber se é sempre possível fatorar um polinômio real em fatores lineares reais (polinômios reais de grau 1) ou fatores quadráticos reais (polinômios reais de grau 2). Porém, Leibnitz vem a desistir de provar a existência de tal fatoração, face ao “contra-exemplo” que ele encontra. Leibnitz achara que a fatoração para o polinômio
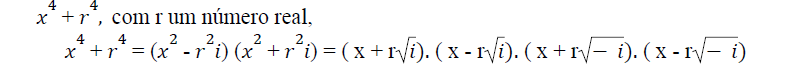

caso contrário ele teria visto que, na fatoração de x4 + r4 multiplicando o primeiro e o terceiro fatores e multiplicando o segundo e o quarto fatores encontramos dois polinômios quadráticos reais tais que

Em 1746 o enciclopedista francês J. d’ Alembert (1717-1783),(atuante na Revolução Francesa de 1789, tal como Leibnitz pesquisando um método para integrar uma função dada pela divisão de dois polinômios com coeficientes reais, o hoje denominado Método das Frações Parciais), encontra uma demonstração difícil do TFA e que contém um erro que só em 1851 seria corrigido, por V. Puiseux (1820-1883). Devido a tal demonstração, na literatura francesa o Teorema Fundamental da Álgebra é chamado teorema de D’Alembert. Atualmente, procura-se resgatar a validade da demonstração de d’Alembert, obviamente inserindo a necessária correção.
J. L. Lagrange (1736-1813) em 1772 levantou objeções à demonstração de Euler e obteve sucesso em preencher várias lacunas na prova de Euler. Mas, sua prova também era incompleta. É importante salientar que em 1777 Lagrange já observara em uma carta que os “números imaginários” já haviam se tornado universalmente aceitos como parte da matemática.
Em 1795, P.S. Laplace (1749-1827) apresentou uma demonstração muito elegante do TFA e bem diferente daquela de Lagrange-Euler. Sua sofisticada demonstração também era incompleta, porém é hoje reabilitada.
Em 1798 o inglês James Wood, publicou em The Philosophical Transactions of the Royal Society o artigo ” On the roots of equations,” apresentando uma prova do TFA para polinômios com coeficientes reais. Sua prova também continha falhas. Recentemente, em 2000, sua prova foi reabilitada por Frank Smithies.
Em 1799 o alemão K. F. Gauss (1777-1855) em sua tese de doutorado apresentou uma demonstração para o TFA que veio a ser considerada a primeira prova correta do teorema. Porém tal demonstração também contém “problemas” que só seriam superados em 1920 por A. Ostrowski. Tal trabalho foi comentado por S. Smale em 1981. Em 1816 Gauss apresenta sua segunda prova, a qual é bastante algébrica, do TFA. Tal prova é correta, porém utiliza um resultado que só seria provado posteriormente ( o Teorema do Anulamento: uma função contínua num intervalo que é maior que zero num ponto e menor que zero em outro, se anula em um terceiro ponto.) Ainda em 1816 Gauss mostra sua terceira prova do TFA, baseada na teoria da integração. Em 1849, ano do jubileu de sua tese de doutorado, Gauss apresenta sua quarta prova do TFA, onde o teorema é enunciado para polinômios com variável e coeficientes complexos.
Em 1806 o suíço J. R. Argand (1768-1822), um dos idealizadores da identificação do plano cartesiano R2 com o plano complexo C, publica um esboço de uma demonstração do TFA em um ensaio sobre a representação dos números complexos. Alguns anos depois, em 1814, Argand publica a primeira prova totalmente correta do Teorema Fundamental da Álgebra enunciado para polinômios com coeficientes complexos, porém utilizando um resultado – sobre a existência do mínimo de uma função contínua – que só em 1861 seria estabelecido por K. Weierstrass (O Teorema do Máximo e do Mínimo, publicado por G. Cantor (1845-1918) em 1870). A prova de Argand de 1814, não reconhecida a princípio devido a tal lacuna, é muito provavelmente a mais simples das demonstrações do TFA. Entretanto, tal prova não é elementar para o padrão moderno da matemática. Esta prova de Argand foi adotada em vários livros textos no século XIX, mas foi aos poucos relegada a um segundo plano no século XX quando o TFA passou a ser apresentado como consequência do Teorema de Liouville – provado por J. Liouville (1809-1882) – em cursos de “Integração em uma Variável Complexa”, em uma demonstração por contradição.
Em 1946 o inglês J. Littlewood (1885-1977) publica uma nova prova do TFA que elementariza a dada por Argand. Porém, a prova de Littlewood é sofisticada ( e ” somewhat artificial in appearance”, em suas palavras). Sua prova é feita por contradição e por indução. Em 2009, o holandês Theo de Jong publicou uma versão modernizada da primeira prova de Gauss para o TFA (1799). Porém, a apresentação não é elementar, pois usa o Teorema dos Multiplicadores de Lagrange e assim, resultados superiores do Cálculo.
Já por volta de 1800 eram conhecidas demonstrações do TFA que não faziam uso da teoria da integração mas que eram no entanto não rigorosas pois os fundamentos da análise matemática ainda não estavam estabelecidos. Uma delas, a de J. Argand, apresentada em 1806 e baseada numa ideia de d’Alembert, é considerada fácil, mas não elementar pois faz uso da extração das raízes n-ésimas como n arbitrário em N, de um número complexo arbitrário. Tal operação de radiciação não é trivial.
8. DEMONSTRAÇÃO DO TFA
A demonstração está baseada em (NASCIMENTO, 2015) e (OLIVEIRA, 2015). Inicialmente assumimos que:
● Toda função p: C →C é contínua em C.
● Teorema de Weierstrass: Seja p: D → R, contínua, D um disco compacto no plano. Então, p assume um valor mínimo em D.
Teorema: Todo polinômio p(z) não constante com coeficientes complexos possui pelo menos uma raiz complexa.
Dividiremos a demonstração em duas partes:
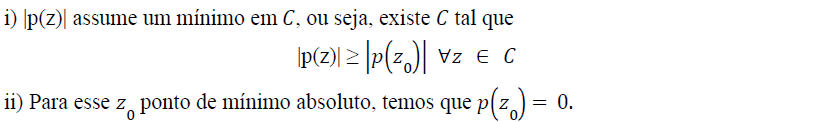

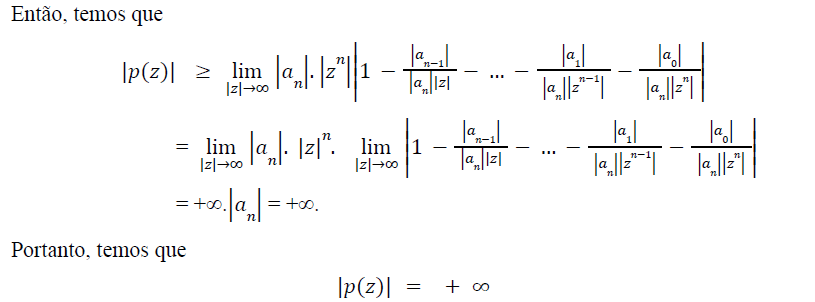

Fonte: OLIVEIRA (2015)




9. CONSEQUÊNCIAS DO TEOREMA
Nesta seção, veremos algumas conseqüências do TFA as quais podem ser vistas em (HEFEZ, 2012) e (NASCIMENTO, 2015).
Proposição: Seja f(z) um polinômio não nulo com coeficientes em C. Se f(z) tem grau n, então f(z) tem no máximo n raízes em C.


10. CONSIDERAÇÕES FINAIS

Além disso, levou os matemáticos a questionarem se realmente essas equações possuem soluções e é nesse aspecto que o TFA ganha destaque, garantindo a existência de pelo menos uma raiz complexa e permitindo escrever uma equação algébrica como o produto de polinômios de grau 1.
Sabemos que no Ensino Médio o TFA é visto de forma axiomática e que a sua demonstração formal se torna inviável, porém é importante salientar que podem ser trabalhados os aspectos históricos do teorema, estimulando a curiosidade do educando e funcionando como elemento motivador, além disso, o professor tem a possibilidade de trabalhar com atividades pedagógicas como o esboço de curvas p(z), por exemplo, fazendo o uso de ferramentas computacionais como o Winplot , Geogebra e, numa perspectiva de complementaridade, o CAS Maple e o GeoGebra (ALVES, 2013).
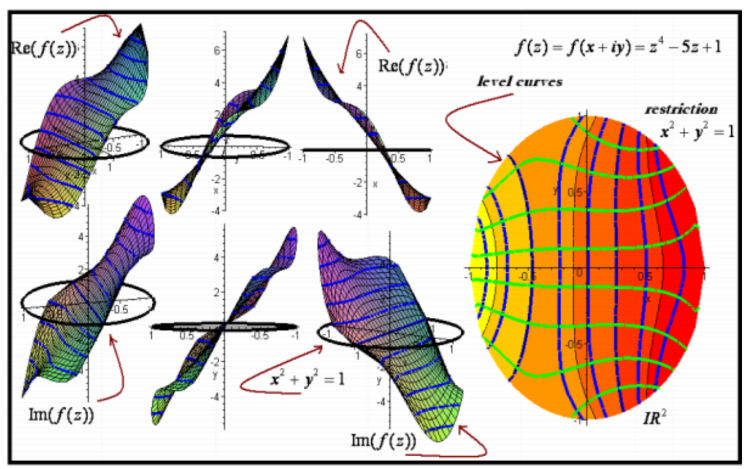
Fonte: ALVES (2013)
11. REFERÊNCIAS
ALVES, Francisco, R. V. Viewing the roots of polynomial functions in Complex Variable: the use the Geogebra and the CAS Maple. Acta Didactica Naposcencia. v. 6, nº 4, 45 – 68, 2013.
NASCIMENTO, C.K.A., Polinômios, equações algébricas e o estudo de suas raízes reais. Dissertação de Mestrado Profissional em Matemática (PROFMAT) – Universidade Federal do Ceará, Fortaleza, 2015.
OLIVEIRA, O.R.B., Teorema Fundamental da Álgebra, 2015. Disponível em <https://www.ime.usp.br/~oliveira/TFACOLEGIAL5.pdf >. Acessado em 06/10/2015.
D’AMBRÓSIO, U., Educação matemática: Da teoria à prática 19 ed. Campinas SP: Papirus, 1996. p.29-30.
LIMA, E. L., A matemática do ensino médio vol. 3, 6o ed. Rio de Janeiro:SBM, 2006.
SOARES, Maria Joana, Análise Complexa, Braga, Portugual, 2007, publicação do Departamento de Matemática da Universidade do Milho. p. 16-17, 21, 36.
HEFEZ, Abramo. VILLELA, Maria Lúcia Torres. Polinômios e Equações Algébricas. Rio de Janeiro: SBM, 2012. p. 15-18, 96-97. (Coleção PROFMAT).
TOFFOLI, Sonia F.L. Conjunto de pontos no plano complexo, 2004. Disponível em: <http://pessoal.sercomtel.com.br/matematica/superior/vcomplex/vc02htm. Acessado em 19/10/2015.
DELBONI, Roberta Regina. Teorema Fundamental da Álgebra. Disponível em: < http://www.ime.unicamp.br/~ftorres/ENSINO/…/TFA_RBTA.pdf >. Acessado em 25/10/2015. p.4.
SEELEY, Robert T. Cálculo de uma variável. Brandeis University, 1976. Traduzido por João Bosco Pitombeira de Carvalho. p.445.
