MATHEMATICS AS AN INTERDISCIPLINARY TOOL IN PHYSICS LEARNING: A CASE STUDY IN THE PUBLIC EDUCATION NETWORK
REGISTRO DOI: 10.5281/zenodo.10644013
Raimundo Nonato Sousa1;
Eduardo de Moura dos Santos Silva2;
Adriano Faustino de Sousa3;
Guilherme Luiz de Oliveira Neto4;
Egnilsom Miranda de Moura5.
Resumo
O Esta pesquisa teve o objetivo de analisar problemas relacionados ao ensino da Matemática como ferramenta para o entendimento dos conteúdos básicos de Física da educação básica. Trata-se de uma pesquisa de natureza qualitativa, que foi realizada no período de agosto de 2022 a fevereiro de 2023; em duas etapas, uma documental, em que se busca entender: de que forma o currículo da disciplina Física interagem com a Matemática. Qual a sua importância na opinião de professores e alunos e suas contribuições para a melhoria da formação básica dos alunos? Para tal, foram analisados os conteúdos teóricos de livros didáticos das disciplinas Matemática e Física e outra de campo, com a aplicação de questionários a estudantes do 3º ano do ensino médio e professores de Física de uma escola pública do município CAXIAS-MA. Os dados foram analisados para verificarmos o uso dos conhecimentos matemáticos e detectar as possíveis dificuldades na aprendizagem dos alunos. Espera-se com esta pesquisa, verificar que a Matemática está inserida diretamente na disciplina de Física, trazendo uma necessidade de sua compreensão, para que os discentes consigam entender os conteúdos dessa disciplina.
Palavras-chave: Matemática; Educação; Ciências da Natureza; Interdisciplinaridade.
1 INTRODUÇÃO
A educação é dever da família e do Estado e deve ser inspirada nos princípios de liberdade e nos ideais de solidariedade humana, para promover o pleno desenvolvimento do educando, seu preparo para o exercício da cidadania e sua qualificação para o trabalho (LDB, 1996).
Doravante das definições da Lei de Diretrizes e Base da Educação (LDB 9394/96) e consolidadas pela nova Base Nacional Curricular Comum (BNCC) de 2018, novas orientações curriculares para o nível médio de ensino foram elaboradas pelo Ministério da Educação (MEC) e estão expressas nas Diretrizes Curriculares Nacionais para o Ensino Médio (DCNEM – Brasil, 1999).
A implementação dessas novas orientações corresponde a uma das metas do Projeto Escola Jovem (Brasil, 2001). Pitágoras já dizia séculos atrás que: “Os números governam o mundo.” O significado dessa frase é grandioso e abrangente, haja vista que afirma que a Matemática está presente nas mais diversas situações do nosso cotidiano.
Coerentemente com o princípio interdisciplinar, cujo objetivo é inter-relacionar, mas não superar as disciplinas, os Parâmetros Curriculares Nacionais para o Ensino Médio (PCNEM) preveem que o ensino da área de Ciências da Natureza priorize o aprofundamento das quatro ciências por meio de uma compreensão profunda de suas características específicas.
Os objetivos explicitamente atribuídos à área de Ciências e Matemática incluem compreender as Ciências da Natureza como construções humanas e a relação entre o conhecimento científico-tecnológico e a vida social e produtiva PCNEM – Brasil,1999).
As atividades que possuem um caráter investigativo têm como principal objetivo o desenvolvimento da autonomia, do senso crítico e da capacidade de avaliar e resolver problemas. Quando os alunos realizam atividades com essas características na área de ciências da natureza, eles exploram, interagem e experimentam o mundo natural (VINTURI et al., 2014).
A motivação para a escolha desse tema, deu-se devido às experiências de trabalhado por mais de 6 anos com Matemática e Física nas mesmas séries do ensino médio na escola estadual Prof. Darcy Araújo no município de Teresina, Piauí. Nesse período verificou-se a relevância de se trabalhar as duas disciplinas em paralelo, porque a maioria dos conteúdos de Física necessita de conhecimentos prévios de Matemática. Notou-se também que utilizando essa estratégia no processo de ensino-aprendizagem dos alunos, ajuda a despertar o interesse pela Matemática.
A problemática exposta no estudo nos levou a questões que se relacionam com o delineamento da disciplina de Matemática, aplicada ao ensino de Física. Foi proposto, então, as seguintes questões norteadoras que serviram para orientar e estruturar esta pesquisa: de que forma os currículos de Física interagem com o currículo de Matemática? Qual a importância da Matemática para o ensino de Física, na opinião de professores e alunos da educação básica?
Para tanto, foram traçados os seguintes objetivos específicos: analisar a relação dos conteúdos de física com os conteúdos de matemática nos livros didáticos das três séries do ensino médio; identificar quais conhecimentos matemáticos são necessários para o ensino- aprendizagem de física na concepção de alunos e professores do ensino médio e Identificar as dificuldades de professores e alunos em relação ao ensino aprendizagem de conteúdos de física que necessitam de conhecimento matemático prévio.
É inegável, que a Física e a Matemática estão intrinsecamente relacionadas desde os seus primórdios. Paty (1995) diz que, em relação ao papel exercido pela Matemática no desenvolvimento da Física, podemos perceber que:
Todavia, a matemática era concebida como um conhecimento que permitia uma leitura direta da natureza, da qual, precisamente era a língua. (…) A constituição progressiva da física-matemática substituiu essa “tradução matemática” da natureza por uma mediação física propriamente dita, isto é, a elaboração explicita de conceitos físicos pensados matematicamente: sendo a matematizarão concebida como inerente aos conceitos, constitutiva desses que serve para construí-los (PATY, 1995, p. 234).
A presente pesquisa visa esclarecer a importância dos conhecimentos matemáticos na aprendizagem dos alunos na disciplina de Física no currículo da educação básica. Descreve o quanto é importante à interdisciplinaridade entre a Matemática e a Física pela necessidade de inter-relacionar os conteúdos das duas disciplinas para a construção do conhecimento.
Ao falar em novas tendências para o ensino da Matemática temos que buscar aquelas que acrescentam algo para os alunos, assim a interdisciplinaridade se faz necessária para formarmos cidadãos com habilidades múltiplas.
Nesse sentido a pesquisa faz-se necessário devido à Matemática ser uma ferramenta fundamental para o ensino da Física, pois precisa ter um saber matemático para resolver questões de Física e assim uma disciplina completa o fundamento da outra.
Quando se fala no termo interdisciplinar busca-se demonstrar o quanto o ensino fragmentado prejudica o ensino aprendizado, pois cada disciplina é trabalhada separadamente onde uma não busca relacionar as outras como elo para a melhor aplicabilidade de certo conteúdo e, assim, a interdisciplinaridade é o termo que faria a junção das disciplinas, onde o conteúdo será aplicado de forma que envolva todas as outras disciplinas com um só ideal para a construção do conhecimento.
Assim, o ensino de Física das escolas de educação básica, apresenta-se, portanto, como terreno fértil para implementação de propostas, estratégias e ações que envolvem promoção do diálogo e a reflexão das práticas que possibilitam a melhoria da aplicação da Matemática no campo das ciências, pois as características comuns à Física, e à Matemática recomendam uma articulação didática e pedagógica interna à sua área na condução ensinoa-prendizado.
Portanto, é fundamental que estudantes e professores do ensino médio conheçam a importância da disciplina de Matemática para o aprendizado de Física, pois os discentes devem saber relacionar os conteúdos de Física com os conteúdos de Matemática nos livros didáticos, identificar quais conhecimentos matemáticos são necessários para o ensinoa-prendizagem de Física, investigar como estão dispostos os conteúdos das disciplinas de Matemática e Física, no nível do ensino médio nos livros didáticos adotados na escola, buscando indícios de materiais potencialmente significativos.
Essa pesquisa visa, principalmente, fazer uma relação entre os principais conteúdo da Matemática e da Física que podem ser aplicados numa metodologia interdisciplinar, levando o aluno a utilizar seus conhecimentos de Matemática para resolver situações-problemas de Física e também usar os conhecimentos de Física para resolver problemas de Matemática, assim eles percebem realmente a relação que existe entre essas duas disciplinas.
Tudo isso foi realizado a partir de uma pesquisa de campo em uma escola Estadual no Município de Caxias, no Estado do Maranhão, onde buscamos apresentar a importância da interdisciplinaridade no meio escolar e principalmente entre o ensino da Física e da Matemática. Foi relacionado conteúdo das duas disciplinas que podem ser articulados por problemas físicos e matemáticos.
A pesquisa está dividida em capítulos da seguinte forma:
No Capítulo 1, é feita a apresentação geral da pesquisa. No Capítulo 2, apresentamos a Revisão de Literatura, este capítulo está dividido em três seções: na primeira seção, falamos um pouco da interdisciplinaridade entre Matemática e a Física, na segunda seção, é mostrado a importância do conhecimento matemático para aprendizagem de Física e na terceira seção é feito resoluções de problemas de Física usando conteúdos de matemática.
No Capítulo 3, apresenta-se a metodologia utilizada, onde serão expostos o passo a passo da pesquisa, desde a abordagem até o processamento, bem como os métodos utilizados
No Capítulo 4, é feita a análise e discussões dos dados coletados, este capítulo é dividido em quatro seções: na primeira seção será apresentado o resultados do questionário respondido pelos alunos; na segunda seção, apresenta-se as respostas do questionário respondidos pelos professores de física participantes da pesquisa; na terceira seção é apresentado as resposta das entrevistas feitas com os professores e na quarta seção apresentamos os resultados da análise dos livros didáticos feito pelos alunos sob as supervisões do professor de Física e do autor da pesquisa.
No Capítulo 5, serão feitas as conclusões e recomendações para futuros pesquisas.
2 REVISÃO DE LITERATURA
Nesse capítulo será apresentada uma revisão de literatura sobre a interdisciplinaridade entre o ensino de Matemática e de Física. Veremos que alguns conceitos físicos têm como ferramenta de resolução, conteúdos matemáticos, demonstrando a importância da interdisciplinaridade entre as duas disciplinas, vejamos.
2.1 RELAÇÕES ENTRE O ENSINO DE MATEMÁTICA E O ENSINO DE FÍSICA: INTERDISCIPLINARIDADE
Labra, Martí e Torregrosa (2010) defendem no ensino de Física o desenvolvimento de um paradigma educativo distinto do tradicional, no qual se possa fomentar o pensamento lógico, analítico e crítico, desenvolver o espírito investigativo, a capacidade de enfrentar e resolver problemas, bem como a autonomia pela busca do conhecimento.
Na maioria das escolas tem-se dado maior ênfase à transmissão de conteúdos e à memorização de fatos, símbolos, nomes, fórmulas, deixando de lado a construção do conhecimento científico dos alunos e a desvinculação entre o conhecimento físico e o cotidiano. Essa prática tem influenciado negativamente na aprendizagem dos alunos, uma vez que não conseguem perceber a relação entre aquilo que estuda na sala de aula, a natureza e a sua própria vida (MIRANDA; COSTA, 2007).
Dados do sistema de Avaliação de Rendimento Escolar do Estado de São Paulo, por exemplo, de 2007 apontam “que 95,7% dos alunos do terceiro ano do Ensino Médio da rede estadual de educação não têm domínio sobre o conteúdo de matemática” (PEDROSO e KRUPECHACKE, 2009, p.1).
Devido a essa realidade, os PCNEM trazem como proposta a ideia de um currículo que favoreça a articulação e interação dos conhecimentos, onde os mesmos possam ser utilizados de forma interdisciplinar na resolução de problemas.
Os PCNEM recomendam que os conhecimentos sejam organizados por grandes áreas, onde a Física, e a Matemática possam se integrar, pois segundo esse documento, essas disciplinas apresentam em comum “a investigação da natureza e dos desenvolvimentos tecnológicos, compartilham linguagens para a representação e sistematização do conhecimento de fenômenos ou processos naturais e tecnológicos” (Brasil, 2002, p. 26)
Nesse contexto, a disciplina de Matemática tem grande importância para professores e alunos nas aprendizagens da disciplina de Física, pois ela deve ser ensinada além de seu caráter instrumental.
Nessa direção, Fazenda (1992), nos diz que a superação da divisão ensino-aprendizagem é favorecida quando há uma valoração da interdisciplinaridade, permitindo uma melhor formação profissional e geral.
Nota-se que a fragmentação do ensino de matemática, ainda tem sido o maior empecilho para a sua aprendizagem, mesmo em tempos como o de hoje, no qual os discursos tanto filosóficos como pedagógicos sobre interdisciplinaridade são muito presentes na formação de professores, mais ainda não se consegue perceber uma real mudança na forma de ensino e aprendizagem dessa disciplina, principalmente em se tratando do ensino de matemática articulado as outras áreas de conhecimento.
O professor que correlaciona um conteúdo com o cotidiano e com outras disciplinas ajuda a motivar e oportuniza ao aluno a construir novos conhecimentos. Assim, a interdisciplinaridade se torna cada dia mais fundamental na educação e, as orientações metodológicas que fazem uso da mesma se tornam cada vez mais necessárias no campo educacional.
A interdisciplinaridade vem se constituindo em foco principal de discussão no campo educacional. A organização do currículo escolar tradicional, composto por disciplinas que se justapõe sem algum tipo de inter-relação mútua, é apontada como responsável de uma formação fragmentada, baseada na dissociação e no esfacelamento do saber (PIRES, 2000, p.74).
Portanto, para resolvermos um problema de matemática, devemos saber ler e explanar o seu significado, para isso, temos que saber interpretar textos e pontuar corretamente, é onde entra a Língua Portuguesa, por exemplo. Desta mesma forma, em Física, para organizarmos e interpretarmos gráficos, tabelas, etc. Devemos ter conhecimentos matemáticos tais como escalas, sistemas de medidas, porcentagem, equações, sistema de equações, proporcionalidade e muitos outros conteúdos matemáticos.
2.2 O CONHECIMENTO MATEMÁTICO E A APRENDIZAGEM EM FÍSICA
No Ensino Médio ainda existe uma grande defasagem no tocante a conhecimentos matemáticos, que impede os alunos de obterem um bom rendimento nas disciplinas que têm a Matemática como pré-requisito, principalmente a Física.
Portanto, está disciplina não pode ser desligada da Matemática, pois as leis físicas são basicamente relações matemáticas entre grandezas que estão presentes em um determinado fenômeno.
O fato dessas disciplinas estarem tão conectadas, torna a Física complicada e desinteressante por parte dos alunos, e isso pode explicar os altos índices de notas baixas nessa disciplina durante os três anos do ensino médio.
A matemática ajuda muito a Física, simplificando a compreensão dos fenômenos. Uma fórmula matemática em um fenômeno físico é uma ajuda para sua compreensão e nunca deve ser assustadora para você. Uma longa explicação é necessária para chegarmos ao fato de que a energia de um corpo em movimento depende de sua massa e de sua velocidade; no entanto, recorrendo à Matemática, obtemos a fórmula:
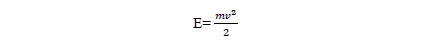
Essa fórmula estabelece que a energia E é diretamente proporcional à massa m e ao quadrado da velocidade v; e também, que a energia depende da massa m e da velocidade v. Assim, aos poucos você terá de aprender a ler uma fórmula e utilizá-la a seu favor (Ramalho et al. 1979, p. 4 apud PIETROCOLA, 2002, p. 94)
O que podemos observar é que os conhecimentos básicos de Matemática são importantíssimos para resolver um problema de Física. O que observamos, no Ensino Médio, é que os alunos até podem entender os princípios físicos envolvidos em uma determinada situação-problema, mas muitos têm grandes dificuldades quando vão aplicar a Matemática para resolvê-la.
Desse modo, em vez de aliada, a matemática se apresenta como mais um problema a ser superado, quando o ideal seria as duas disciplinas caminharem juntas para uma melhor compreensão dos fenômenos da natureza, a qual é o objetivo do estudo da Física.
Podemos notar as dificuldades na aprendizagem de Física logo no último ano do ensino fundamental II (9º ano), período em que os alunos de escolas públicas terão o primeiro contato efetivo com a disciplina. Nessa ocasião, já pode ser percebida a grande dificuldade, por parte de muitos estudantes, em relação a assuntos, como operações com notação científica, razão, proporção, unidades de medidas e noções de funções polinomiais.
Estes são assuntos necessários para um bom rendimento nos conteúdos iniciais da cinemática. É comum, nesse período, encontrarmos aqueles que mal sabem as quatro operações básicas (soma, subtração, multiplicação e divisão), incluindo, noções básicas de grandezas e de funções.
Por muitas vezes, esses problemas são compartilhados pela maioria, de modo que, muitas escolas optam por algum tipo de intervenção, para melhorar a situação de notas dos alunos, mas recuperar todo o conhecimento matemático básico seria extremamente complicado, devido à questão do tempo que seria necessário para a referida intervenção.
No ensino da Física, a linguagem matemática é muitas vezes considerada como a grande responsável pelo fracasso escolar. É comum professores alegarem que seus alunos não entendem física devido à fragilidade de seus conhecimentos matemáticos. Para muitos, uma boa base matemática nos anos que antecedem o ensino de Física é garantia de sucesso no aprendizado. (Ramalho et al. 1979, p. 4 apud PIETROCOLA, 2002, p. 90)
Além dos problemas enfrentados pelos alunos e professores devidos as deficiências encontradas em Matemática por parte dos alunos, existem também outras deficiências, facilmente perceptíveis, que influenciam a aprendizagem de Física no Ensino Médio.
Como, por exemplo, poderíamos destacar a interpretação de textos, cuja deficiência se prolonga por todo o Ensino Médio, sendo um dos principais motivos dos baixos rendimentos dos alunos nas provas do Exame Nacional do Ensino Médio (ENEM).
2.3 RESOLUÇÃO DE EXERCÍCIOS DE FÍSICA USANDO A MATEMÁTICA
Para mostrar que a interdisciplinaridade entre as disciplinas Matemática e Física é de grande importância, foram resolvidos problemas de física empregando conteúdos de matemática durante a análise dos livros didáticos. Demonstrando-se assim a importância da união destas duas disciplinas e a sua consequência para um ensino aprendizado que busca a desenvolver a autonomia de seus alunos com o intuito de prepara-lós para interagir com a sociedade em constante evolução.
PROBLEMA 1: (Relação entre o movimento retilíneo uniforme e função afim) Um corpo em movimento retilíneo uniforme, descreve um movimento conforme função s = s0 + vt, em que t é o tempo; s, a posição do móvel no instante t, s0 , a posição do móvel no instante t0 ; v, a velocidade do móvel. Supondo o movimento representado pela equação s(t) = 5t + 10, com t em segundos e s em metros. Calcule a posição do corpo no instante t = 20s.
Resolução: A função afim é representada pela equação f(x) = ax + b. Pode-se observar que a equação dada na situação problema pode ser representada pela equação da função afim s(t) = f(x); 5t = ax; b = 10, logo podemos resolver este problema substituindo na equação
s(t) = 5t + 10 ⟹ s (20) = 5. (20) + 10 ⟹ s (20) = 100 + 10 ⟹ s (20) = 110m.
PROBLEMA 2: (Relação entre movimento uniformemente variado de um corpo e função quadrática) Uma pedra foi abandonada de um edifício, sua altura em metros, depois de t segundos é dada pela função H(t) = −5t² + 125. Qual a altura do edifício e em que instante a pedra atingirá o solo?
Resolução: Pode-se observar que a função dada na situação problema pode ser substituída pela equação da função quadrática ou equação de segundo grau, que permite que o docente trabalhe a resolução de uma equação do segundo grau incompleta aprofundando assim no conhecimento matemático do aluno.
A função de segundo grau é representada pela equação f(x) = ax² + bx + c que pode ser substituída pela função dada no problema onde f(x) = H(t); ax² = −5t²; onde bx = 0; c =125. Logo podemos resolver este problema empregando conhecimentos prévios de função de 2º grau.
A altura do edifício é calculada quando t = 0
H(t) = −5t² + 125 ⟹ H (0) = −5.0² + 125 ⟹ H (0) = 125 m.
momento em que a pedra atingirá o solo será quando H(t) = 0. Como
H(t) = −5t² + 125 ⟹ −5t² + 125= 0 ⟹ t2 = -125/-5 ⟹ t² = 25 ⟹ t = 5s.
PROBLEMA 3: (Relação entre aceleração escalar média e progressão aritmética) Um carro parte do repouso com aceleração de 5,0 m/s². Qual é o valor da velocidade média do carro, em m/s, após 10 segundos?

Como podemos observar, a sequência é uma progressão aritmética que está aumentando de 5 em 5, ou seja, uma constante chamada de razão da P.A. Esse conceito é usado na Física no Movimento Retilíneo Uniformemente Variado, em que a aceleração é constante.
PROBLEMA 4: (Relação entre equação matemática e dilatação linear de sólidos) Os materiais sólidos, quando sofrem um aumento em sua temperatura, sofrem a chamada dilatação térmica, que é a variação das dimensões desses materiais. Essa dilatação depende do material em questão, do comprimento inicial do material e da variação de temperatura que este sofreu. O cálculo dessa dilatação é dado pela equação matemática:
ΔL = L0. α. ΔT.
Sendo que:
ΔL , representa a dilatação térmica sofrida pelo material;
L0, representa o comprimento inicial do objeto;
α representa o coeficiente de dilatação linear, essa grandeza depende do tipo de material, e a grandeza que nos mostra, qual material dilata mais e qual dilata menos, para a mesma variação de temperatura (veja o Tabela 1).
ΔT, representa a variação de temperatura, calcula-se subtraindo a temperatura final da temperatura inicial do material.
Em nosso cotidiano existem inúmeras situações que envolvem a dilatação térmica dos materiais. Quando colocamos uma quantidade de café muito quente em um copo de vidro comum, pode ocorrer de ele trincar. Isso ocorre porque a parte interna do copo se dilata ao ser aquecido. No entanto, o vidro é um mau condutor de calor, de forma que a parte externa do mesmo demora para ser aquecida. Dessa forma, ocorre diferença de dilatação entre as partes interna e externa do copo, o que acaba por fazê-lo trincar.
Tabela 1 – Valores médios dos coeficientes de dilatação linear de alguns sólidos
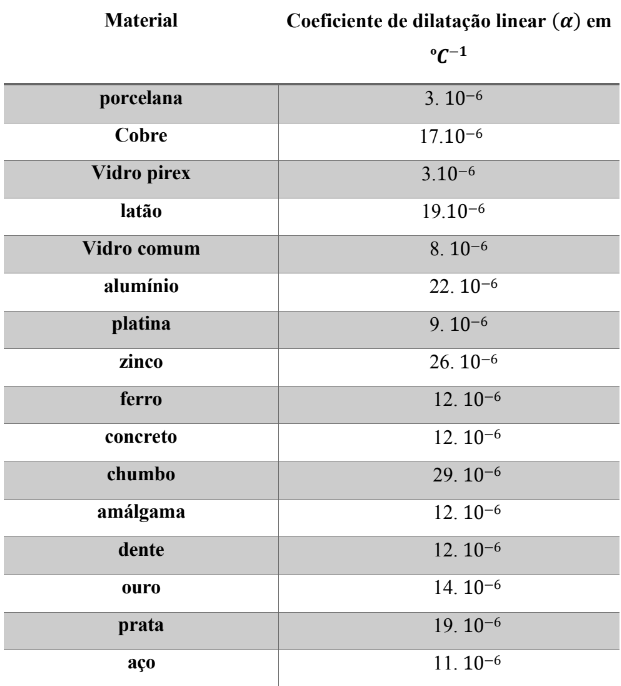
As calçadas, quadras poliesportivas e até mesmo as lajes sofrem dilatação quando a temperatura aumenta e contração quando a temperatura diminui. Nesse processo de dilatação e contração podem acontecer fissuras que, no caso das lajes, acabam deixando a água passar quando ocorre chuva.
Para evitar essas fissuras e rachaduras, os pedreiros colocam juntas, no caso das quadras, e divisórias, no caso das calçadas, quando estão construindo as mesmas. Durante a construção de pontes e viadutos deixam-se pequenas fendas para que essas estruturas possam dilatar quando a temperatura aumentar, sem que aconteçam as rachaduras.
Nas ferrovias existem pequenos espaços que separam um trilho de outro, possibilitando que eles se dilatem sem provocar danos à estrutura conforme Figura 1.
Figura 1 – Junta de expansão

Caso não seja deixado esse espaço, entre as barras que compõem os trilhos, quando estas dilatarem, devido uma variação de temperatura, pode acontecer uma deformação nos trilhos (ver Figura 2).
Figura 2 – Trilhos deformados

Os trilhos de uma ferrovia foram assentados em um dia frio de inverno sob temperatura de 0ºC. Precavido o engenheiro instruiu os operários para deixarem uma folga de 9,0mm entre os trilhos consecutivos. O comprimento de cada trilho é 10,00m, e o coeficiente de dilatação linear do aço pode ser observado na tabela abaixo.
Analise as afirmações a seguir e classifique-as, em verdadeira ou falsa.
I – Quando a temperatura ambiente atingir 25º C, a folga entre os trilhos vai diminuir para 6,0mm.
II – A folga entre os trilhos permanece constante, qualquer que seja a temperatura.
III – Os trilhos irão se tocar se, devido a exposição ao sol ou ao atrito com as rodas do trem, a temperatura deles atingir 75º C.
Resolução I:
Como ΔL = L0. α. ΔT. ,então ΔL = 10.12. 10−6.25 = 0,003m = 3mm.
Portanto a nova folga entre os trilhos consecutivos passa a ser de 9-3=6mm.Daí conclui-se que a afirmação é verdadeira.
Resolução II:
A afirmação é falsa. A folga entre os trilhos varia com a temperatura devido ao fenômeno da dilatação térmica.
Resolução III:
Quando a temperatura varia de ºC para 75ºC, ΔL = 10.12. 10−6.75=9mm.Logo não vai mais existir folga entre os trilhos e eles irão se tocar. Portanto a afirmação é verdadeira.
Na resolução das situações – problemas acima vejamos claramente a necessidade dos conhecimentos matemático prévios, veja que não é necessário o aprofundamento de nenhum princípio físico, no problema 1 é uma aplicação direta da função afim, no problema 2 o aluno tendo conhecimento da função quadrática facilmente ele resolveria a questão. O objetivo é apenas mostrar uma aplicação do conteúdo matemático no contexto físico, despertando a curiosidade dos mesmos.
3 METODOLOGIA
3.1 CARACTERIZAÇÕES DA PESQUISA
Nesta seção, será apresentado o contexto de investigação, na pesquisa tipo qualitativa: a escola pública investigada, os indivíduos participantes da pesquisa, o problema de investigação. Mostra, também, a maneira como foi desenvolvida a pesquisa tipo qualitativa (análise dos livros didáticos, questionários e entrevistas de professores e questionário dos alunos do 3º ano do ensino médio, observação dos participantes durante as aulas de matemática e física), revelando como se fez o levantamento dos dados e a observação dos mesmos, através da análise de conteúdo.
A presente pesquisa foi de natureza aplicada, tendo em vista a finalidade de apresentar alternativas que ajudem a melhorar a aprendizagem dos alunos.
Quanto a abordagem a pesquisa foi de natureza qualitativa, pois os resultados serão analisados de maneira subjetiva por questionários, observações, fotos, diários de bordo entre outros.
A respeito da pesquisa qualitativa, Minayo (2002, p. 21-22,24) traz o seguinte posicionamento
pesquisa qualitativa responde a questões muito particulares. (…) ela trabalha com o universo de significados, motivos, aspirações, crenças, valores e atitudes, o que corresponde a um espaço mais profundo das relações dos processos e fenômenos que não podem ser reduzidos a operacionalização de variáveis. (…) abordagem qualitativa aprofunda-se no mundo dos significados das ações e relações humanas, um lado não perceptível e não captável em equações, médias e estatísticas.
Observando o posicionamento de Minayo podemos identificar características da presente pesquisa que se identificam com as características dos estudos qualitativos. Quando se diz que a pesquisa qualitativa se preocupa com as relações e ações, então o contexto da pesquisa deve ser o contexto no qual o fenômeno acontece.
Entendemos que esta é uma característica de grande importância e por isso realizamos a pesquisa a partir dessa perspectiva, assim como temos por objetivo conhecer a concepção dos estudantes e dos professores de Física da educação básica a respeito da relação entre a Física e a Matemática. Se faz necessário, para nos alinharmos com uma pesquisa de cunho qualitativo, que nossa pesquisa lide diretamente com professores e alunos que estão atuando na educação básica no ensino de Física.
A pesquisa, além de qualitativa, também deve ser considerada uma pesquisa de campo, pois ela “pretende conseguir informações e/ou conhecimento acerca de um problema para o qual se procura uma resposta ou as relações entre eles” (MARCONI; LAKATOS, 2015, p. 69).
Assim, quando dissemos que teríamos como objetivo conhecer qual a concepção que os professores e alunos da educação básica possuem a respeito da relação entre a Física e a Matemática, não podemos prescindir da pesquisa de campo, a qual se realiza no contexto em que o fenômeno acontece, ou seja, pesquisando os professores que estão atuando na educação básica, uma vez que nossa principal preocupação é com as concepções dos professores e dos alunos da educação básica.
A pesquisa foi realizada na escola pública Estadual Centro de Ensino Eugenio Barros do município de Caxias-Maranhão, que contempla o ensino médio, nos turnos manhã e tarde, possui quinhentos e quinze alunos matriculados, trinta e nove professores, um diretor, um diretor-adjunto, uma secretária e dois coordenadores. É uma escola localizada na Rua Manoel Gonçalves, n.º 670, Bairro Centro, que atende alunos da zona urbana e rural.
Os participantes deste trabalho foram quatro professores de física e trinta e dois estudantes de uma turma de 3º ano do ensino médio.
Os dados foram coletados de duas maneiras: 1) por meio de atividades desenvolvidas com os alunos e 2) por meio de questionários aplicados aos alunos, questionário e entrevistas feitos com os professores participantes deste estudo.
Atividade 1: As atividades desenvolvidas com os alunos, ocorreram da seguinte forma:
primeiro foi aplicado um questionário sobre a interdisciplinaridade entre matemática e outras disciplinas, em seguida dividimos em três grupos, e sob supervisão dos professores e do autor da pesquisa, os alunos analisaram os conteúdos teóricos de livros de física e matemática das três séries do ensino médio. Os livros analisados foram os da coleção Conexão com a Física
PNLD-2018 dos autores Blaidi Sant’Anna, Gloria Martini, Hugo Carneiro Reis e Walter Spinelli e os da coleção contexto e aplicações do autor Luiz Roberto Dante PNLD-2018. A análise foi feita buscando correlações que apontem a necessidade de conhecimento prévio de matemática para a compreensão dos mesmos.
Atividade 2: Após a análise dos livros, foram feitas oficinas envolvendo alunos e professores onde foram abordados situações problemas de Física envolvendo conteúdos de Matemática buscando compreender se realmente havia relação entre as disciplinas e quais dificuldades existiam para tal compreensão; para analisar e ter uma real visão da situação dos alunos frente a esta interdisciplinaridade.
As informações obtidas foram tratadas e submetidas a análise de conteúdos e posteriormente categorizadas segundo semelhanças e diferenças no teor das respostas. Em seguida foram elaborados tabelas, quadros e gráficos para ilustrar os resultados.
3.2 INSTRUMENTOS DE PRODUÇÃO DE DADOS
Como o projeto visava identificar as dificuldades dos discentes e docentes em relação a assuntos de Física que necessitam de conhecimento matemático prévio, inicialmente, aplicou- se um questionário (apêndice A), em uma turma de 3º ano do Ensino Médio, composta por 32 alunos, sendo que 29 estavam presentes e o outro questionário (apêndice B) seguido de uma entrevista a quatro professores de Física.
O questionário aplicado aos alunos foi para identificar se realmente havia esta dificuldade e quais eram; para analisar e ter uma real visão da situação dos alunos frente a esta interdisciplinaridade. Aos professores foi aplicado um questionário para saber se trabalham a interdisciplinaridade entre Matemática e Física durante suas aulas, quais habilidades consideram importantes para desenvolver um trabalho interdisciplinar. Logo após, foi feita a análise das respostas do questionário e construção de tabelas, quadros e gráficos para ilustrar os resultados.
Posteriormente, os alunos participantes do trabalho dividiram-se em três grupos. Os alunos do primeiro grupo analisaram os livros do primeiro ano, os do segundo grupo analisaram os livros do segundo ano e os alunos do terceiro grupo analisaram os livros do terceiro ano sob supervisão dos professores, fazendo uma justificativa do uso dos conhecimentos matemáticos nos diversos conteúdos destas disciplinas, explicitando a
importância da Matemática no conhecimento geral e no cotidiano dos discentes e docentes.
4 RESULTADOS E DISCUSSÕES
Neste capítulo mostraremos de forma sistematizada os resultados obtidos durante toda nossa pesquisa. Apresentamos por meio de quadros, tabelas e gráficos, visando otimizar a visualização, além do uso de medidas descritivas extraídas a partir dos dados trabalhados ao longo da pesquisa. Primeiramente, optamos por dividir o processo de análise e discussão em seções.
4.1 RESPOSTA DO QUESTIONÁRIO DOS ALUNOS
Nesta Seção apresentamos os resultados do questionário realizado com 29 alunos do Terceiro Ano do Ensino Médio da escola Estadual Centro de Ensino Eugênio Barros, localizada na cidade de Caxias, Estado do Maranhão.
No turno da tarde, a escola possui duas turmas do 3º ano médio. A turma foi escolhida conforme o horário do autor da pesquisa e do professor de Física da referida turma que participou da pesquisa.
O questionário foi composto por dez questões, sendo as cinco primeiras perguntando sobre as dificuldades que os alunos sentem nas aprendizagens das disciplinas Física e Matemática. A segunda parte com mais cinco questões foi perguntado aos discente se eles tinham conhecimento sobre a interdisciplinaridade.
Após a aplicação do questionário (Figura 3), foi feita a análise das respostas, onde foi obtido o seguinte resultado (Tabela 2) e (Gráfico 1) referentes as cinco primeiras perguntas.
Figura 3 – Aplicação do questionário aos alunos

Tabela 2 – Resultados do questionário (número total de sim e de não
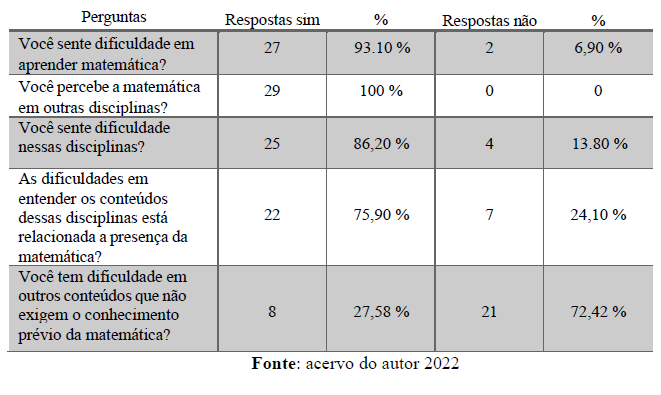
Segundo as respostas do questionário, 100% percebem a matemática sendo necessária em outras disciplinas, 93,1% dos alunos informaram ter dificuldades em matemática, 86,2% sentem dificuldades nessas disciplinas e 75,9% afirmam que estas dificuldades estão relacionadas com a necessidade do uso de conhecimento matemático, ou seja, percebemos grandes dificuldades, por parte dos alunos, quando precisam utilizar conhecimentos de matemática.
Isso mostra a necessidade de uma maior integração entre os currículos de Física e Matemática de modo que, sempre que possível, determinado conteúdo que esteja sendo trabalhado na Matemática, seja também aplicado na disciplina de Física simultaneamente.
Gráfico 1 – Respostas do questionário dos alunos
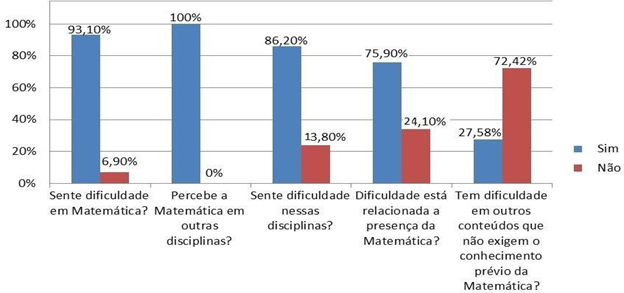
Portanto, é de fundamental importância que professores de Física e de Matemática façam planejamentos combinando os conteúdos das duas disciplinas.
Em relação às dificuldades encontradas em Física, afirmam estar relacionadas à quantidade de cálculos (fórmulas). Muitos falam que o maior problema é lembrar das fórmulas, e quando lembra ainda tem as dificuldades de desenvolver os cálculos matemático, como argumenta Barufi (1999) o professor de matemática precisa encontrar situações significativas e motivadoras, com problemas interessantes, a fim de que seus alunos, tentando dar respostas a esses problemas, consigam estabelecer significados para o conhecimento desejado, compreendendo-o e, portanto, articulando-o a própria rede.(…) O processo de problematização é fundamental se o professor pretende que o aluno construa os significados para daí ser possível a compreensão do conhecimento desejado.
Fazenda (1992) nos diz que a superação da divisão ensino-aprendizagem é favorecida quando há uma valoração da interdisciplinaridade, permitindo uma melhor formação profissional e geral. Daí a importância do trabalho em conjunto de professores de física e de matemática.
4.2 RESPOSTA DO QUESTIONÁRIO DOS PROFESSORES
O questionário (do Apêndice B) foi aplicado a quatro professores de Física do ensino médio da Escola Estadual Centro de Ensino Eugenio Barros, localizada na Cidade de Caxias, Estado do Maranhão, sendo dois do turno da manhã e dois do turno da tarde. Foi comunicado aos mesmos que a pesquisa era de forma anônima, pois seria preservada a integridade dos participantes.
Para identificar os professores da pesquisa, denotamos cada um por F1, F2, F3 e F4 e, por meio de quadros e gráficos, apresentamos os resultados da análise do questionário aplicado aos docentes.
O Quadro 1 apresenta a formação dos docentes participantes da pesquisa. Verifica-se que 100% dos professores tem especialização e 75% tem mestrados, isso mostra que estes professores estão buscando se aperfeiçoar.

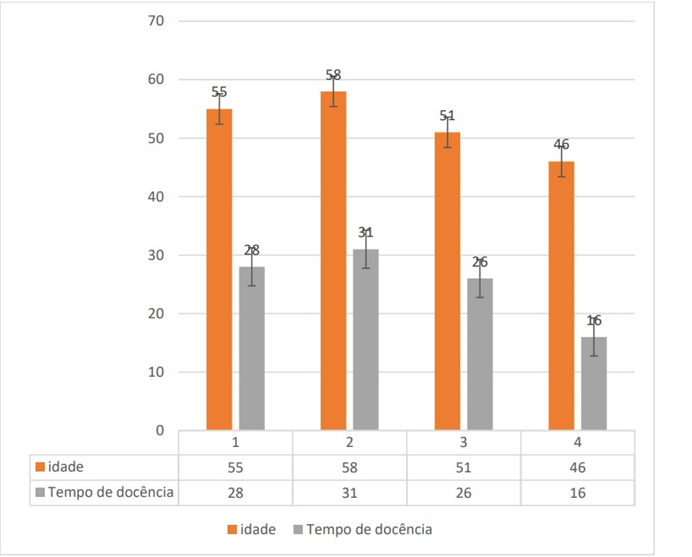
O Gráfico 2 mostra a idade e o tempo de docência dos professores avaliados na pesquisa. Dos professores pesquisados, 75% têm mais de 50 anos e 100% têm 16 anos ou mais em sala de aula.
Gráfico 2 – Idade e tempo de docência dos professores
Quadro 2 – Respostas dos docentes sobre interdisciplinaridade
Perguntas do (apêndice A) Respostas obtidas Pergunta: 5-Que você entende por trabalho interdisciplinar e como executá-lo? É um trabalho que envolve diferentes disciplinas tendo como objetivo melhorar o ensino e aprendizagem (Prof. F1)
Trabalho em conjunto entre professores de diferentes disciplinas e pode ser executado através de atividades na escola que possa envolver os alunos(a) com as disciplinas envolvidas dos professores (Prof. F2) É um trabalho que envolve mais de uma disciplina (Prof. F3) É relacionar os conteúdos ministrados em sala de aula com o cotidiano dos alunos e sua vivência, complementado com os conhecimentos das outras disciplinas ministradas (Prof. F4). Deve ser executado a partir da boa vontade e colaboração dos professores Pergunta 6: Você já trabalhou com a “interdisciplinaridade” ou com questões “interdisciplinares” em suas aulas?
( ) Sim. Especificamente em quais conteúdos ou áreas?
( ) Não. Justifique sua resposta:Sim na área de ciências da natureza e Matemática (Prof. F1) Sim. Procurando sempre relacionar as áreas envolvidas. (Prof. F2) Sim. Questões de física envolvendo matemática e vice versa (Prof. F3) Sim. Conteúdos de Física que sempre envolvendo conteúdo de Matemática e vice versa (Prof. F4) Pergunta 7: No seu contexto de trabalho, você considera possível relacionar conteúdos entre as disciplinas diferentes?
( ) Sim. Especifique:
( ) Não. Justifique sua resposta:Sim. O ensino fica mais prazeroso, assim contribui de forma positiva no processo de ensino aprendizagem (Prof. F1)
Sim. Por exemplo, a Matemática pode auxiliar os alunos(a) nos conteúdos de Física e vice e vice versa. (Prof. F2)
Sim. O ensino se torna mais global, tanto para quem ensina quanto para quem aprende (Prof. F3)
Sim. Torna o aprendizado mais significativo, contribui para a integração das disciplinas de uma maneira geral (Prof. F4)Pergunta 8: No seu contexto de trabalho, você considera possível relacionar conteúdos entre as disciplinas diferentes?
( ) Sim. Especifique:
( ) Não. Justifique a resposta: Sim. Conteúdos de Física e Matemática sempre andam juntos, para resolver problemas de Física é necessário aplicação da Matemática. (Prof. F1)
Sim. Por exemplo, a matemática pode auxiliar os alunos(a) nos conteúdos de Física e vice e vice versa. (Prof. F2)
Sim. Como Física e Matemática são disciplinas que andam junta, fica muito fácil relacionar os conteúdos das duas na mesma serie. (Prof. F3)
Sim. Através de projetos interdisciplinares, a realização de projetos mobiliza conhecimentos de várias disciplinas (Prof. F4)Pergunta 9: Na sua concepção, quais habilidades docentes você considera importante para desenvolver um trabalho “interdisciplinar”? Fazer um bom planejamento e executá-lo em conjunto com os demais professores (Prof. F1)
Os professores sejam mais flexíveis, os planejamentos sejam elaborados e executados em conjunto (Prof. F2) Capacidade de colaboração, com iniciativa para se especializar cada vez mais (Prof. F3) Trabalhar de forma coletiva, ter um bom planejamento, pesquisar etc. (Prof. F4)Pergunta 10: A sua Escola desenvolve atividades para suprir as dificuldades dos educandos?
( ) Sim. Especifique o tipo de atividade:
( ) Não. Justifique a resposta:Sim, com projetos envolvendo disciplinas de áreas afins (Prof. F1)
Sim, com projetos que envolve várias disciplinas (Prof. F2)
Sim, com projetos interdisciplinares (Prof. F3)
Sim, há um número considerado de projetos interdisciplinar (Prof. F4)Pergunta 11: Você trabalha os conteúdos de física planejado com o professor de matemática para relacionar a Matemática envolvida na Física?
( ) Sim.
( ) Não. Justifique a resposta:Não. As vezes pergunto qual conteúdo está trabalhando ((Prof. F1)
Não. Dificilmente nos encontramos (Prof. F2)
Não. Pergunto as vezes para os alunos qual é o conteúdo de matemática que eles estão vendo (Prof. F3)
Não. Tem ano que nem vejo o professor de matemática (Prof. F4)
Os resultados supracitados são frutos de toda a pesquisa realizada com os professores, não havendo nenhuma interferência por meio de palavras por parte do autor. Todas as respostas dadas pelos professores foram escritas de forma integral, tentando encontrar padrões, concordâncias e discordâncias, avaliando as necessidades e dificuldades gerais ao falar sobre o assunto abordado na pergunta.
Com relação ao entendimento do trabalho interdisciplinar e sua execução, todos os quatro docentes envolvidos na pesquisa têm conhecimento do referido tema, concordam com a sua grande relevância dentro do contexto escolar, pois propicia ao aluno uma aprendizagem mais significativa, uma preparação para a vida, uma antecipação do que há por vir.
Todos dizem trabalhar em sala de aula a interdisciplinaridade principalmente conteúdos que relacionam Matemática e Física. Assim como cita (PIRES, 2000, p.74), a interdisciplinaridade, vem se constituindo em foco principal de discussão no campo educacional.
A organização do currículo escolar tradicional, composto por disciplinas que se justapõe sem algum tipo de inter-relação mútua, é apontada como responsável de uma formação fragmentada, baseada na dissociação e no esfacelamento do saber.
Quando é perguntado sobre a relação entre as disciplinas Física e Matemática, todos sabem a necessidade do conhecimento da Matemática na resolução de problemas de Física. Sobre as habilidades desenvolvidas durantes as aulas, consideram que fazer planejamentos em conjuntos com os demais professores seria uma boa estratégia para concretizar habilidades interdisciplinares.
Na fala dos docentes fica claro que em suas escolas há projeto interdisciplinar, mais ambos são unânimes em dizer que não há projetos envolvendo professores de Física e de Matemática trabalhando em paralelos os conteúdos das duas disciplinas, algo que seria de grande importância visto que as duas andam juntas no processo de ensino- aprendizagem.
4.3 ENTREVISTA COM OS PROFESSORES DE FÍSICA
A entrevista foi feita com os quatros professores de Física da escola, respectivamente (professores F1, F2, F3 e F4), pois estes professores também responderam ao questionário, por isso mantiveram as mesmas denominações.
A entrevista ocorreu individualmente e de duas formas, presencial com os professores do turno vespertino e por meio de aplicativo de conversa com os professores do turno matutino devido à falta de tempo, tanto por parte do autor quanto dos entrevistados.
As mesmas perguntas foram direcionadas aos quatro entrevistados, com os seguintes questionamentos:
1ª) Você trabalha a interdisciplinaridade entre Matemática e Física durante suas aulas? Se sim, de que forma? Se não, por quê? 2ª) Você concorda que trabalhando a interdisciplinaridade entre Matemática e Física contribui para a aprendizagem dos alunos na sua disciplina? Se sim, de que forma? Se não, por quê? 3ª) Você planeja suas aulas em conjunto com o professor de Matemática? Se sim, de que forma? Se não, por quê? 4ª) O estado proporciona um tempo para planejamento e dialogo para os professores?
As respostas dadas pelos entrevistados estão dispostas no quadro 3
Quadro 3 – Resposta das entrevistas com os docentes
Questionamento Respostas obtidas 1ª) Você trabalha a interdisciplinaridade entre Matemática e Física durante suas aulas? Se sim, de que forma? Se não, por quê? Sim, mostrando qual o conteúdo de Matemática está inserido no conteúdo de Física trabalhado (Prof. F1). Sim, resolvendo situações-problemas mostrando os cálculos das operações Matemática envolvidas (Prof. F2).
Sim, mostrando aos discentes qual é a parte da Matemática envolvida na aula (Prof. F3).
Sim, na resolução das questões de Física comento que sempre há um conteúdo de Matemática sendo desenvolvido. (Prof. F4).2ª) Você concorda que trabalhando a interdisciplinaridade entre Matemática e Física contribui para a aprendizagem dos alunos na sua disciplina? Se sim, de que forma? Se não, por quê? Concordo plenamente, planejando as aulas com o professor de Matemática, mais é difícil fazer esse trabalho paralelo, pois não temos tempos pra dialogar sobre o tema (Prof. F1).
Concordo, visto que a matemática está parente em todos conteúdos de Física. Tento trabalhar junto com o professor de Matemática mais quase sempre é inviável por falta de tempo (Prof. F2).
Trabalhar a interdisciplinaridade com o professor de Matemática é muito importante para a aprendizagem dos alunos, por que a Matemática aparece em quase todas questões de Física (Prof. F3).
Concordo sim, a interdisciplinaridade entre essas disciplinas melhora a aprendizagem dos alunos (Prof. F4)3ª) Você planeja suas aulas em conjunto com o professor de Matemática? Se sim, de que forma? Senão, por quê? Tem anos que os nossos horários coincidem, aí planejamos algumas vezes, mais tem anos que nem vejo o professor de Matemática muitas vezes se torna impossível pelo fato de trabalharmos os três turnos e em escolas diferentes (Prof. F2).
Não, as vezes quando encontro pergunto qual conteúdo de Matemática está ministrando (Prof. F3) Geralmente pergunto o que está ministrando de conteúdo, mais planejar juntos não (Prof. F4).4ª) O estado proporciona um tempo para planejamento e dialogo para os professores? Não temos tempo disponível para planejar trabalhos interdisciplinar, temos diálogo por acaso (Prof. F1 ). Seria bom se tivesse, mas isso não acontece (Prof. F2). As vezes acontece encontro por áreas, mas nem todos professores participam (Prof. F3).
Não temos horário para planejarmos em conjunto, seria bom se tivéssemos (Prof. F4).
Pelas respostas obtidas nas entrevistas, notamos que os docentes trabalham a interdisciplinaridade entre Matemática e sua disciplina, e sabem que a interdisciplinaridade entre as disciplinas contribui de forma positiva no processo de ensino-aprendizagem. Mas percebe-se, que existe uma necessidade de diálogo entre os professores, para que dessa forma pudessem planejar suas atividades interdisciplinares para buscar uma aprendizagem mais significativa. Para os autores (Ramalho et al. 1979, p. 4 apud PIETROCOLA, 2002, p. 94), a matemática ajuda muito a Física, simplificando a compreensão dos fenômenos. Uma fórmula matemática em um fenômeno físico é uma ajuda para sua compreensão e nunca deve ser assustadora para o aluno.
Pelos relatos, o maior problema é a falta de tempo para fazerem planejamentos, pois conforme as conversas e dados colhidos no questionário e entrevistas na escola, a maioria dos professores tem carga horaria maior ou igual a 40 horas semanais dividida entre os três turnos e em mais de uma escola, o que dificulta os encontros para planejamento das atividades que envolvam as duas disciplinas.
4.4 RESULTADO DA ANÁLISE DOS LIVROS DIDÁTICOS
Para justificar e esclarecer esta necessidade do conhecimento matemático, fez-se um levantamento dos conteúdos de física, para explicar o uso dos conhecimentos matemáticos e detectar as possíveis causas destas dificuldades. A (Figura 4) mostra alunos fazendo a análise dos livros didáticos com a supervisão de professor.
Figura 4 – Alunos analisando os livros didáticos

Durante a análise dos livros didáticos de Física do ensino médio, notou-se as seguintes relações com os conteúdos da matemática:
Quadro 4 – Relação entre os conteúdos de Física e os de Matemática
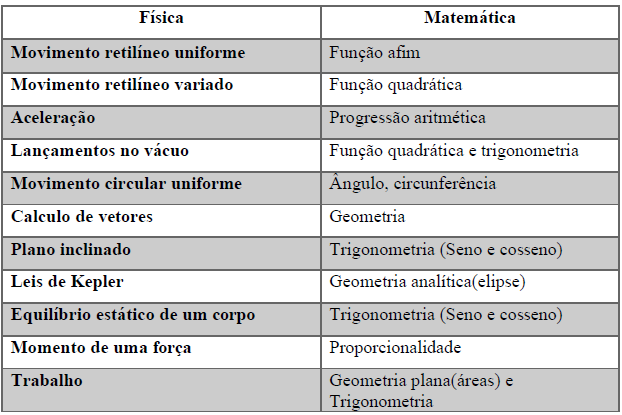
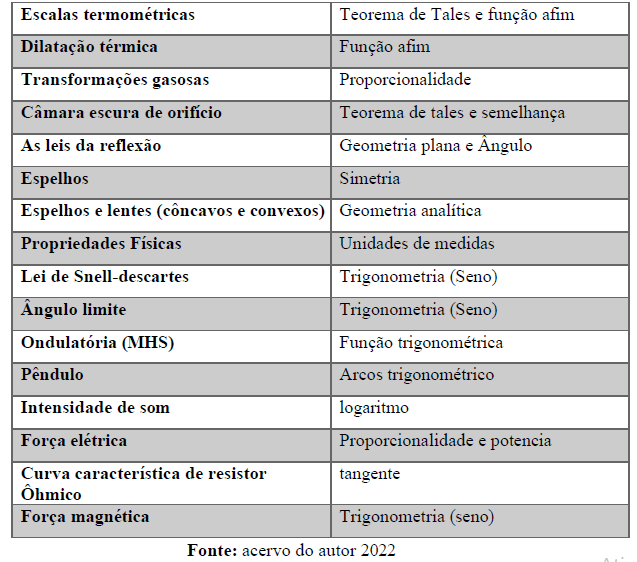
Dentre os assuntos encontrados destacam-se com maior frequência o uso das fórmulas, cálculos com vetores e as unidades de medidas. Em princípio, deve-se ressaltar as fórmulas presentes na Física que possuem inúmeros conteúdos matemáticos. Em todas as fórmulas nota- se as operações básicas: adição, subtração, multiplicação e divisão. Todas estão ligadas a algum tipo de função, sendo a maioria, funções afins e quadráticas. Alguns exemplos são:
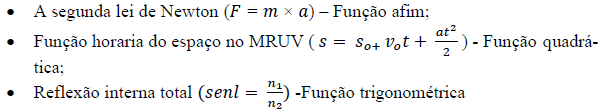
Potências, raízes, senos, cossenos e módulos também são recorrentes em algumas fórmulas, porém em menor escala. Alguns exemplos são:

Diante a hipótese de que a matemática na física dificulta o aprendizado do aluno, vimos que há um vínculo gigantesco entre as duas matérias, onde a matemática se envolve em quase toda a parte da física, com suas operações, equações e funções.
Segundo o Físico Alemão Wilhelm Rontgen “o físico precisa de três coisas para o seu trabalho: A matemática, matemática e a matemática” seguindo tal pensamento, concluímos que para o estudo da física obrigatoriamente temos que ter uma matemática desenvolvida. A precariedade de conhecimento dos alunos em tal matéria faz com que gere um grande problema envolvendo a dificuldade na absorção do conhecimento da física.
Dado o exposto, conclui-se que alunos com uma base matemática pouco desenvolvida pode acarretar certos problemas com aprendizado na Física. Para haver uma total compreensão do conteúdo abordado em aulas de Física deve ocorrer anteriormente um bom domínio da matemática pelo aluno. Isto é confirmado nas palavras dos autores (Ramalho et al. 1979, p. 4 apud PIETROCOLA, 2002, p. 90), no ensino da Física, a linguagem matemática é muitas vezes considerada como a grande responsável pelo fracasso escolar.
É comum, professores alegarem que seus alunos não entendem física devido à fragilidade de seus conhecimentos matemáticos. Para muitos, uma boa base matemática nos anos que antecedem o ensino de Física é garantia de sucesso no aprendizado.
3 CONCLUSÃO
Com fundamento nos dados que foram pesquisados: questionário com alunos, questionário e entrevistas com professores de Física, análise de livros didáticos de Física e de Matemática, pode-se verificar que existe uma relação significativa entre os conteúdos de Física e de Matemática.
Notamos que não existe um sincronismo suficiente na mesma etapa de ensino entre os conteúdos de Física e de Matemática que possa haver uma interdisciplinaridade entre as duas disciplinas. Para ser possível, deve haver um avanço no que se refere ao diálogo e planejamento entre professores de Física e de Matemática para que em muitos casos possa ser feitos alterações nas ordens de trabalhar os conteúdos correlacionados.
Com base nos objetivos lançados, buscou-se traçar que relação existe entre os conteúdos de Física e os conteúdos de Matemática das três series do ensino médio. Diante disso, a pesquisa teve como objetivo geral conhecer a importância da disciplina de Matemática para o aprendizado de Física na concepção de estudantes e professores do Ensino Médio.
Tivemos como objetivos específicos analisar a relação dos conteúdos de Física com os conteúdos de Matemática nos livros didáticos das três series do Ensino Médio, identificando quais conhecimentos matemáticos são necessários para o ensino-aprendizagem de Física na concepção de alunos e professores, identificar as dificuldades de professores e alunos em relação ao ensino-aprendizagem de conteúdos de Física que necessitam de conhecimento matemático prévio.
A pesquisa que foi de natureza aplicada, quanto a abordagem, de natureza qualitativa e quanto aos objetivos, descritiva e exploratória. Para obtenção da coleta de dados, feito em dez encontros na escola estadual CENTRO DE ENSINO EUGENIO BAIRRO na cidade de Caxias, estado do Maranhão, foi aplicado questionário aos professores e aos alunos do 3º ano dos do Ensino Médio, feito uma entrevista com os professores de Física e por fim feito a análise dos livros didáticos comparando os conteúdos dos três livros de Física com os conteúdos de Matemática no período de agosto a novembro de 2022.
Todos os dados obtidos, observações e aplicações, foram discutidos estatisticamente e de forma qualitativo com outros teóricos alinhados com a temática proposta. Notou-se que a Matemática está inserida diretamente nas disciplinas de ciências da natureza, em especial na disciplina Física, trazendo uma necessidade de sua compreensão, para que os discentes consigam entender os conteúdos de Física.
Este trabalho busca contribuir na investigação da relação interdisciplinar entre as disciplinas de Física e Matemática para direcionar atividades futuras, pois há pouca produção de conhecimentos nestas disciplinas que possuem pouca aceitação pelos discentes.
Todos sabemos que a Matemática está presente em diferentes atividades que realizamos diariamente. Conseguir enxergá-la no cotidiano é um movimento que nos faz perceber a sua importância e a sua conexão nas diferentes áreas do conhecimento. Aqui proponho que reflitam como desenvolver as competências e habilidades matemáticas para além das aulas de Matemática. Para esse trabalho é essencial ter clareza dos seus objetivos e qual é a intencionalidade pedagógica por trás de cada atividade.
Conectado a isto está o seu planejar e o registrar para poder analisar, posteriormente, se conseguiu alcançar o que havia previsto. Trabalhando projetos interdisciplinares, é colocar em prática propostas que explorem conhecimentos de diferentes áreas. As habilidades a serem trabalhadas dependerão do tema e, principalmente, da intencionalidade do professor.
A partir dos dados colhidos e analisados, torna-se necessário fazer um trabalho de conscientização da comunidade escolar, para que todas as dificuldades sejam minimizadas ou sanadas.
REFERÊNCIAS
BARUFI, M. C. B. A construção/negociação de significados no curso universitário inicial de Cálculo Diferencial e Integral. Tese de Doutorado – Faculdade de Educação, Universidade de São Paulo, 1999.
BARDIN, Laurence. Análise de contúdos.2 ed. São Paulo.2011.279p.
BENETI, MARCELO. A Importância do Trabalho Interdisciplinar. Disponível em:<http://meuartigo.brasilescola.com/educacao/importancia-trabalho-interdisciplinar.htm>. Acesso em: maio 2022.
BRASIL. Ministério da Educação. Secretaria de Educação Fundamental. Parâmetros Curriculares Nacionais: Matemática. Brasília: MEC/ SEF, 1997. p. 18-26.
BRASIL, Ministério da Educação. Secretaria de Educação Média e Tecnológica. Parâmetros Curriculares Nacionais: Ensino Médio, Ciências da Natureza, Matemática e suas Tecnologias, Brasília, 1999.
BRASIL. Guia de Livros Didáticos Ensino Médio: PNLD 2018: Física Ensino Médio. Brasilia: Ministerio da Educação, Secretaria de Educação Básica,2017. Disponível em:<http://www.fnde.gov.br/programas-do-livro-didático/pnld/guia-do-livro-didático/ item/ 11148-guia-pnld-2018>. Acesso em: novembro 2022.
Brasil. (2017). Base Nacional Comum Curricular. http://portal.mec.gov.br.
DANTE, L.R, Matemática contexto e aplicações, v.1, SÃO PAULO,2018. DANTE, L.R, Matemática contexto e aplicações, v.2, SÃO PAULO,2018.
DANTE, L.R, Matemática contexto e aplicações, v.3, SÃO PAULO,2018.
FAZENDA, I. C. A Integração e interdisciplinaridade no ensino brasileiro: efetividade ou ideologia? São Paulo: Loyola, 1992.
GUIMARÃES, O.; PIQUEIRA, J.R.; CARRON, W.Física1. SÃO SAULO,2018.
GUIMARÃES, O.; PIQUEIRA, J.R.; CARRON, W. Física 2. SÃO PAULO,2018.
GUIMARÃES, O.; PIQUEIRA, J.R.; CARRON, W. Física 3. SÃO PAULO,2018.
LABRA, Carlos Becerra; GRAS-MARTÍ, Albert; MARTÍNEZ-TORREGROSA, Joaquín. Efectos sobre la capacidad de resolución de problemas de “lápiz y papel ” de una enseñanzaaprendizaje de la física con una estructura problematizada. Revista Brasileira de Ensino de Física, v. 32, n. 2, 2401-1 a 2401-11, 2010.
MARCONI, Marina; LAKATOS, Eva. Fundamentos de metodologia científica. 8. ed. São Paulo: Atlas, 2017a.
MINAYO, MC.de, S. O desafio do conhecimento: pesquisa qualitativa em saúde. São Paulo-Rio de Janeiro, HUCITEC-ABRASCO,1992.
MIRANDA, D. G. P; COSTA, N. S. Professor de Química: Formação, competências/ habilidades e posturas. 2007.
Parâmetros Curriculares Nacionais: Ensino Médio. Ministério da Educação. Secretaria de Educação Média e Tecnológica. Brasília: Ministério da Educação,1999.
PATY, Michel. 1989, A Matéria roubada, EDUSP, SP, 1995.
PEDROSO, Carlos Marcelo; KRUPECHACKE, José Eloir. Análise de alternativas para recuperação de fundamentos de matemática no ensino de Cálculo em cursos de Engenharia. COBENGE, 2009.
PIETROCOLA, M. A matemática como estruturante do conhecimento físico. Cad. Cat. Fís., Florianópolis, v. 19, n. 1, p. 89-109, ago. 2002.
PIRES, CÉLIA M. C. Currículos de matemática: da organização linear à ideia de rede. São Paulo: FTD, 2000.
RAMALHO, F. Santos, J.I.C., FERRARO, N.G. SOARES, P.A.T:1979, Os Fundamentos da Física, Editora Moderna,1979,3ª edição, São Paulo.
VINTURI, E. F. et al.; Sequências didáticas para a promoção da alfabetização científica: relato de experiência com alunos do ensino médio. Experiências em Ensino de Ciências, v. 9, n. 3, p. 11-25, 2014.
¹Mestre em matemática /IFPI-PROFMAT. Email: caflo.2021114pmat17@aluno.ifpi.edu.br
²Mestre em matemática /IFPI-PROFMAT. Email: caflo.2021114pmat08@aluno.ifpi.edu.br
³Mestre em matemática /IFPI-PROFMAT. Email: caflo.2021114pmat01@aluno.ifpi.edu.br
4Professor Dr. do PROFMAT do IFPI de Floriano. Email: guilherme@ifpi.edu.br.
5Professor Dr. da Universidade Federal do Piauí – UFPI de Teresina. Email: egnilson@ufpi.edu.br.
