REGISTRO DOI: 10.5281/zenodo.10888933
Johnny Luis Mércuri
RESUMO
O presente trabalho tem por finalidade apresentar a irracionalidade da raiz quadrada de dois (aplicando o método de prova por absurdo) a determinação exata dela na reta numérica usando apenas régua e compasso e apresentar a espiral de Teodoro e como construí-la, sendo, a mesma bastante eficaz para determinar a posição exata na reta numérica de algumas raízes irracionais. Para isso iniciamos mostrando como dividir um certo segmento ao meio (aplicando para a construção do quadrado de lado 1 unidade) e a existência de valores que não são racionais. Em seguida a demonstração de que a raiz quadrada de dois é irracional, determinar a posição desse valor na reta numérica usando métodos de construção geométrico com régua e compasso e por fim apresentar a espiral de Teodoro e como construí-la usando argumentos anteriormente mostrados, obtendo assim o comprimento exato dos seguimentos da forma √n com n ∈ N, onde 2 ≤ n ≤ 17. Tal trabalho também tem por base auxiliar o professor que deseje utilizar o Geogebra como ferramenta de suporte para o ensino de raízes irracionais, pois descreve os passos necessários para a construção podendo assim determinar o comprimento das raízes, tornando interessantes as aulas, pois o professor poderá expor a construção em sala com o software e os alunos acompanharem os argumentos de construção usando régua e compasso.
Palavra-chave: Irracionalidade, raiz quadrada de 2, números irracionais
ABSTRACT
The present work aims to present the irrationality of the square root of two (applying the method of proof by contradiction), to determine its exact location on the number line using only ruler and compass, and to present the spiral of Theodorus and how to construct it, as it is quite effective in determining the exact position on the number line of some irrational roots. To achieve this, we begin by demonstrating how to divide a certain segment in half (applying it to construct a square with side length 1 unit) and the existence of values that are not rational. Next, we demonstrate that the square root of two is irrational, determine the position of this value on the number line using geometric construction methods with ruler and compass, and finally present the spiral of Theodorus and how to construct it using arguments previously shown, thus obtaining the exact length of segments of the form √n with n ∈ N, where 2 ≤ n ≤ 17. This work also aims to assist teachers who wish to use Geogebra as a supporting tool for teaching irrational roots, as it describes the necessary steps for construction, allowing them to determine the lengths of the roots. This makes the classes more interesting, as the teacher can present the construction in class using the software while the students follow along with the construction arguments using ruler and compass.
Keyword: Irrationality, square root of 2, irrational numbers
1 INTRODUÇÃO
Nos dias de hoje, o professor se encontra exposto diariamente a um problema extremamente comum nas escolas de todo o país, a falta de interesse pela matemática por parte de alguns alunos. Muitas vezes por rações de uma grande defasagem de aprendizado carregada ano, após ano, sem que essa lacuna no ensino possa ser preenchida ou até mesmo causada pelos próprio pais, onde muitos argumentam como por exemplo: (a matemática é muito difícil eu não aprendi então não tem importância você não aprender, tirando um nota razoável já esta bom matemática e chata mesmo) trazendo assim uma concepção de que a matemática não é algo essencial fazendo com que sua dedicação e interesse se esvaia pela disciplina.
Assim, com tal propósito de motivar o aluno e auxiliar seu aprendizado sem recorrer a métodos de ensino tradicionais como a repetição de fórmulas e o uso da lousa, será apresentada uma atividade em concordância com a BNCC para o auxílio e aprendizagem das raízes irracionais usando o software GeoGebra como ferramenta de suporte para o professor e como forma de tornar as aulas mais atrativas e interessantes para o educando.
2.1 DETERMINANDO UM RACIONAL E A EXISTÊNCIA DOS IRRACIONAIS
Segundo (Eves; 2011) os números inteiros são abstrações que surgem do processo de contar coleções finitas de objetos, mas, nem sempre essa contagem se da por um número inteiro podendo nos resultar em valores “quebrados”, um exemplo seria a divisão de uma linha reta de comprimento 1 cm em quatro partes iguais. Para realizar esse processo basta construirmos duas circunferências de raio 1 cm cada, onde o centro de C 1 seja em A e o centro de C 2 seja em B (Figura 1).
Figura 1
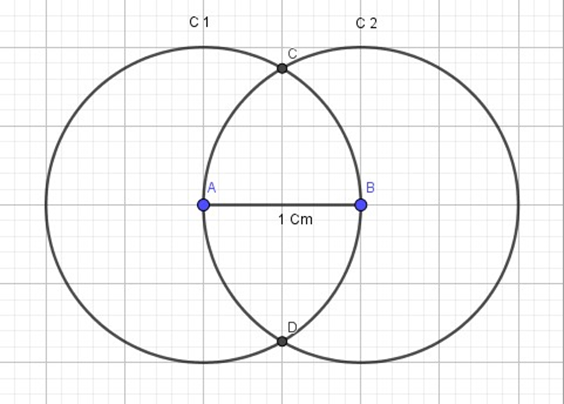
Assim, as duas circunferências terão dois pontos de interseção (pontos C e D), traçando o segmento CD obtemos uma perpendicular a AB (onde CD ∩ AB = {E}) e mais, essa perpendicular divide exatamente o segmento AB ao meio, tendo assim AE = EB = 1/2 cm, como mostra a figura 2.
Figura 2

Mas, queremos dividir esse segmento em 4 partes iguais, basta proceder da mesma forma, mas agora tomando três circunferências de raio 1/2 cm centras em A, E e B (figura 3), aplicando a mesma idéia, temos:
Figura 3
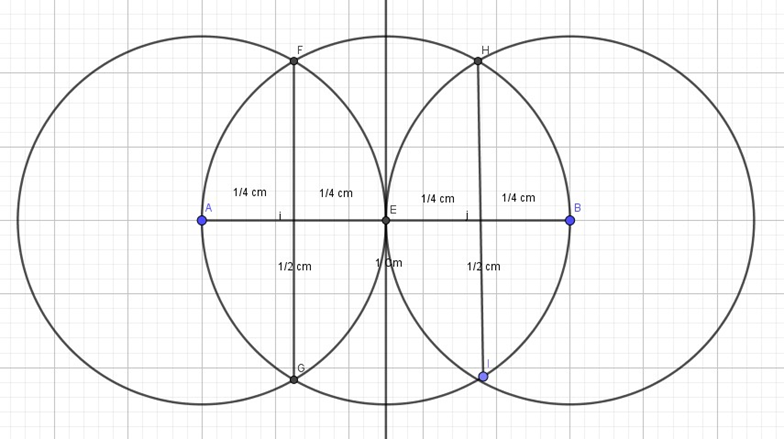
Logo, obtemos 4 segmentos iguais de 1/4 cm cada, onde o valor do segmento é um número racional. Sabemos que todo racional é dado pelo quociente p/q onde q ≠ 0, mas antigamente (na época dos pitagóricos) os primeiros matemáticos acreditavam que dividindo cada intervalo unitário em q partes poderíamos preencher todo um segmento, não sobrando “buracos”, assim cada racional representa um ponto na reta.
Um tempo depois os pitagóricos descobriram que existiam pontos na reta que não são representados por racionais, em particular não há um número racional ao qual corresponda um ponto P da reta onde OP é a diagonal de um quadrado cujos lados medem uma unidade (Eves; 2011, pg 105) (Figura 4).
Figura 4
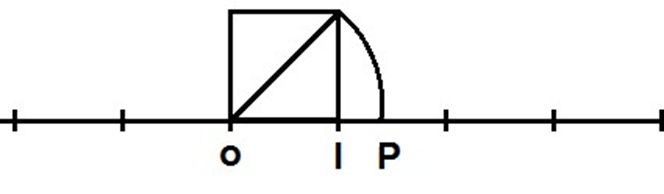
Surgindo então a necessidade de novos números para associar a esses pontos, de tal forma que esses novos números não sejam os racionais, surgindo assim os irracionais.
2.2 A RAIZ QUADRADA DE DOIS É IRRACIONAL
Para demonstrar tal fato, usaremos o método de demonstração por absurdo, onde vamos supor que a √2 é racional, chegando assim em uma contradição, logo sendo irracional.
Suponhamos que a √2 é um número racional com p e q primos entre si, logo temos que:
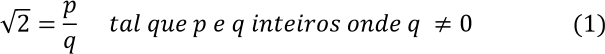
Elevando ao quadrado de ambos os lados de (1) temos:
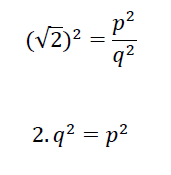
Assim, temos que p² é o dobro de um número inteiro, portanto p² é par e ainda p também é par por ser divisível por 2, mas isso é um absurdo pois por hipótese temos que p e q são primos entre si, logo concluímos que √2 não é racional, sendo assim irracional.
2.3 CONSTRUÇÃO DA RAIZ QUADRADA DE DOIS NA RETA NUMÉRICA USANDO REGUÁ E COMPASSO
Queremos determinar a posição da √2 na reta numérica, primeiramente façamos a construção de um quadrado de lado 1 unidade usando apenas as idéias apresentadas do trabalho.
– Construção do quadrado de lado 1unidade
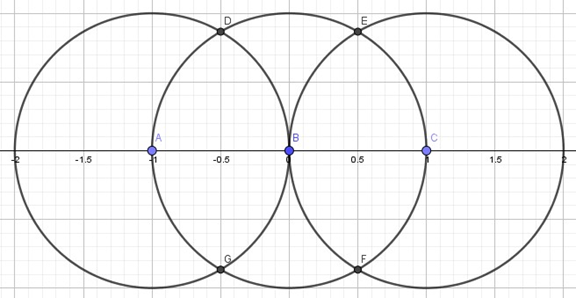
a) Na reta numérica com a ponta seca do compasso em 0,1 e -1 trace as circunferências de raio um.
Figura 5
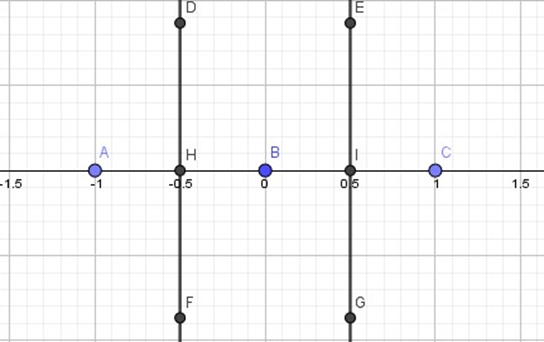
b) Trace agora as perpendiculares, uma contendo os pontos D e G e a outra os pontos E e F, dessa forma o segmento AB e BC serão divididos ao meio (veja a figura 7).
Figura 6

Figura 7
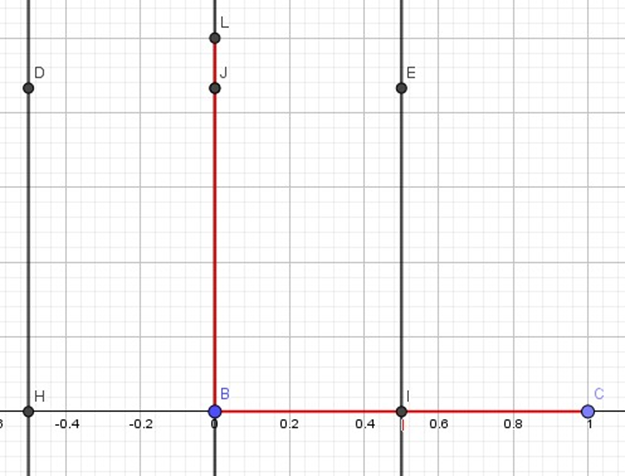
c) Faça duas circunferências de raio 1 unidade, uma centrada em H e outra em I na interseção (nos pontos J e K) trace a perpendicular.
Figura 8

d) Agora com a ponta seca do compasso em B, faça a abertura até C, com a mesma abertura, marque o ponto L na reta que contém os pontos B, J e K assim podemos afirmar que o segmento BL = BC = 1 unidade.
Figura 9
e) Assim, para determinar o ponto N, devemos proceder da mesma forma que obtemos o ponto L, após determinado os 4 pontos podemos afirmar que BC = BL = CN = NL = 1 unidade obtendo assim nosso quadrado de lado medindo 1 unidade.
Figura 10
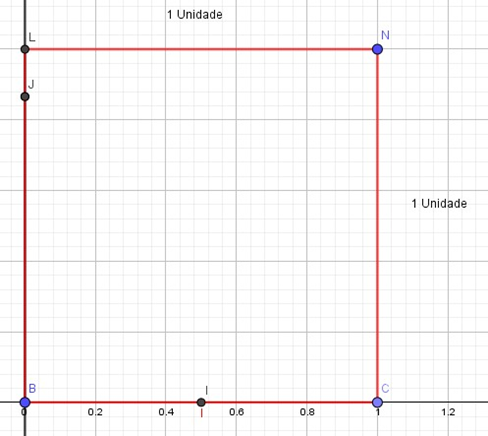
Determinando a √2 na reta numérica
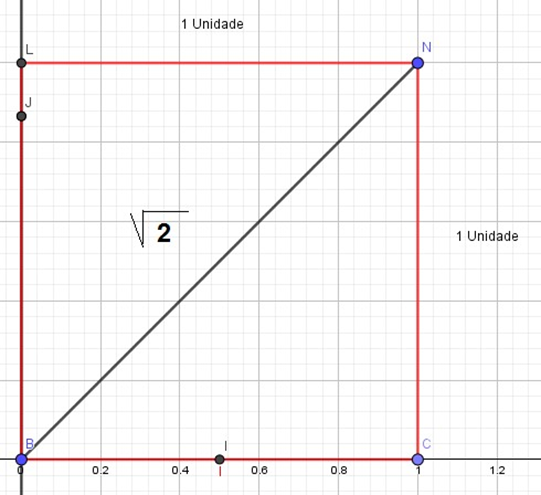
a) Trace a diagonal BN usando a régua, assim, obtemos dois triângulos (retângulo) onde BN é a hipotenusa comum, aplicando o teorema de Pitágoras temos que (BN)2 = 12 + 12 onde BN = √2 , assim o segmento BN é o valor que queremos obter na reta numérica.
Figura 11
b) Agora com a ponta seca do compasso em B, faça a abertura do mesmo até N e trace a circunferência de raio √2. Na interseção entre a circunferência e a reta numérica marque o ponto O, assim o segmento BO (figura 12) na reta numérica vale √2 . Logo conseguimos obter a posição exata da √2 na reta numérica.
Figura 11
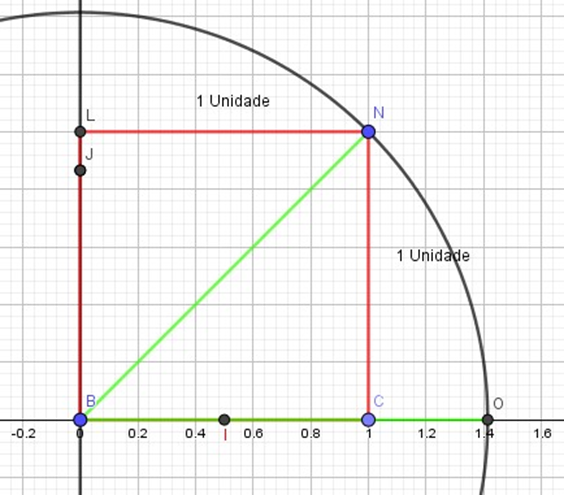
Assim, seguindo esses passos conseguimos determinar exatamente a posição da √2 unidades na reta numérica usando apenas régua e compasso.
3.1 GENERALIZAÇÃO DO MÉTODO PARA A OBTENÇÃO DAS RAIZES IRRACIONAIS E A CONSTRUÇÃO DA ESPIRAL DE TEODORO
Como visto anteriormente, podemos determinar a posição exata da √2 na reta numérica usando ferramentas simples como régua e compasso, sendo assim uma proposta interessante para auxiliar no aprendizado das raízes irracionais no ensino fundamental, em específica no 9° ano, como apresentado na BNCC (Base Nacional Comum Curricular; Pg 316) .
Assim, usando o mesmo argumento geométrico anterior podemos determinar o comprimento de qualquer raiz quadrada irracional e obter sua posição exata na reta numérica, mas para isso tomaremos como base a construção da espiral de Teodoro, onde a mesma proporciona todos os comprimentos na forma √n para todo n ∈ N.
3.2 CONSTRUINDO A ESPIRAL DE TEODORO USANDO O GEOGEBRA
Primeiramente, tomemos o triângulo ABC retângulo em B de cateto medindo 1 e tracemos um segmento de comprimento 1 perpendicular a hipotenusa AC, formando assim o triângulo ADC retângulo em A. Aplicando teorema de Pitágoras temos que DC tem o valor de √3 (Figura 13).
Figura 12
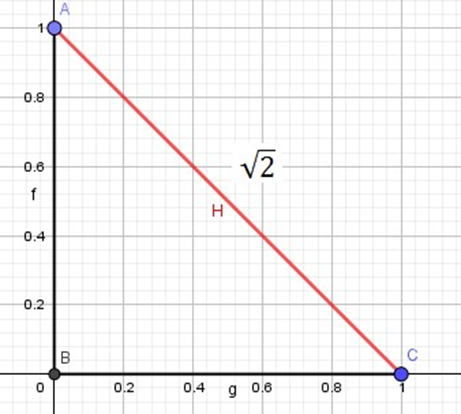
Figura 13

Assim, basta aplicarmos tal algoritmo para a construção de qualquer segmento irracional:
i- Traçar uma perpendicular a hipotenusa do triângulo anterior de medida 1 unidade
ii- Fechar o triângulo de catetos 1 unidade e hipotenusa do triângulo anterior, obtendo assim um novo triângulo retângulo
Repetindo tal processo até a √17, obtemos:
Figura 14

Veja que tal método é bastante eficaz para determinar o comprimento exato das raízes da forma √n para todo n ∈ N, sendo assim um forte auxiliador para a determinação de tal raiz na reta numérica, bastando apenas a transposição do segmento desejado com o compasso para a reta.
4 CONCLUSÃO
Logo, podemos concluir que a raiz quadrada de dois é um número irracional e determinar a mesma na reta numérica é possível usando apenas a régua e o compasso, podendo ainda ir mais além. Através da espiral de Teodoro podemos determinar qualquer segmento irracional desejado conseguindo assim transportá-lo para a reta numérica determinando sua posição exata, sendo esse método bastante simples e interessante a ser aplicado no ensino fundamental ( 9° Ano ) como método de motivação e aprendizado de números irracionais
REFERÊNCIAS
Eves, H. Introdução á história da Matemática. Tradução Hygino H. Domingues. 5° Ed. – Campinas, SP: Editora Unicamp, 2011. p. 103 – 107
BNCC (Base Nacional Comum Curricular). Disponível em:<http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_ site.pdf>. Acesso em : 27 mar. 2020.
GeoGebra – Aplicativos Matemáticos. Disponível em :<https://www.geogebra.org/?lang=pt>. Acesso em 3 abr. 2020.
