REGISTRO DOI: 10.5281/zenodo.10019943
Eliomar Gotardi Pessoa1
Coautora: Glaucia Brandão Freitas2
Resumo: A utilização de lajes planas vem tomando grandes proporções no quesito tecnologias da construção e modelagem numérica. No princípio tais lajes eram executadas empiricamente e, posteriormente, submetidas a ensaios de carga. Com o desenvolvimento da computação , a modelagem dessas estruturas tornou-se mais acessível aos projetistas e as vantagens inerentes ao sistema tornaram-se visíveis. Neste trabalho serão estudados processos teóricos e numéricos para o cálculo de lajes planas, bem como os principais fatores a serem considerados na modelagem. Será definida uma modelagem numérica e comparado a uma modelagem pela teoria de flexão das placas. A comparação entre os procedimentos será apresentada no final deste trabalho. A solução da Equação Diferencial de Lagrange, adotada para resolução da teoria das flexão das placas neste trabalho, tem como solução a série de fourier e equações diferenciais parciais. A solução dessa equação, que descreve o comportamento físico de uma placa (elemento estrutural de uma edificação), é obtida de acordo com a condição de contorno pré-estabelecida, através de métodos de Navier.
Palavras-chave: Teoria das flexões das Placas. Métodos de Navier. Equação diferencial de Lagrange.
1. Introdução
1.1 Considerações Iniciais
Dos exemplos de estrutura em que o uso da computação tornou-se fundamental podemos citar as lajes planas, ou seja, aquelas que apresentam teto liso. Anteriormente,o cálculo desse tipo de estrutura era feito através de métodos aproximados ou em programas computacionais que exigiam enorme quantidade de tempo e grandes computadores para o processamento dos dados. Entretanto, com o aprimoramento dos programas de cálculo e análise, e dos próprios computadores, o projeto das lajes planas tornou-se mais comum no ambiente dos calculistas, o que acentuou o uso dessas soluções estruturais e proporcionou a discussão de diversos assuntos sobre o seu uso.
As lajes, Figura 01, podem ser maciças ou nervuradas, podendo ainda a armadura ser passiva, protendida ou uma combinação das duas.
Em estruturas convencionais é comum adotar vigas junto ao elemento da laje que redistribuem os esforços nesses elementos e posteriormente nos pilares. Existem também lajes que não utilizam vigas, como exemplo, podem citar lajes nervuradas que apresentam trechos maciços junto aos pilares para combater a punção e os momentos negativos (Figura 2).
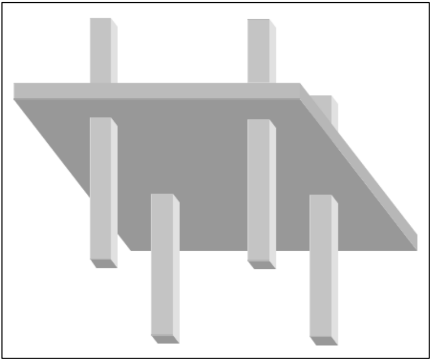
Figura 1 – Exemplo de modelo tridimensional de uma laje.
Fonte: HENNRICHS, Carlos Alexandre (2003, p.25)

Figura 2 – Exemplo de laje nervurada.
Fonte: https://www.vivadecora.com.br/pro/arquitetura/laje-nervurada/
No presente trabalho serão abordadas exclusivamente lajes de concreto armado maciças, com armadura passiva (não protegida), comportamento linear e no regime elástico, ou seja, toda a deformação é recuperada. Não serão adotados capitéis nem painéis de transição (“drop panels”), pois serão estudados exclusivamente esforços da laje em serviço, e não a necessidade de reforços nesta para o dimensionamento. As cargas aplicadas na laje serão sempre normais ao seu plano médio, portanto cargas provenientes de esforços horizontais, como o vento, ou mesmo deslocamento da estrutura, não serão consideradas. O estudo se concentra na modelagem da laje e na obtenção de resultados, especialmente momentos fletores e deslocamentos. Para tal estudo, será utilizado a teoria da Flexão das Placas.
As placas se encontram submetidas, fundamentalmente, a esforços de flexão, distinguindo-se das chapas, estruturas também planas, mas submetidas a cargas contidas no seu plano médio. O trabalho de flexão das placas exige que estas sejam delgadas.
As placas podem diferenciar-se pela sua forma (de contorno poligonal ou circular, maciças ou com espaços vazios); pela disposição de seus apoios (placas apoiadas no seu contorno, placas em balanço, placas contínuas em uma ou duas direções); pela forma do apoio (pontual ou lineares); pelo tipo de apoio (apoio simples ou engastamento). Cada placa pode, além disso, estar submetida a diferentes tipos de carga, como por exemplo, carga pontual, uniforme, etc
Para o cálculo dos esforços nas placas existem dois grupos de métodos. Os métodos clássicos, fundamentados na teoria da elasticidade, supondo que o material é homogêneo e isótropo e se comporta elasticamente, da mesma forma que se faz, para o cálculo de esforços em outros tipos de elementos estruturais. Ja métodos de ruptura, fundamentados na teoria da plasticidade, supõem, ao contrário, o material comporta-se como um corpo rígido – perfeitamente plástico.
A Equação de Lagrange resolve o problema proposto, apresentando poucas soluções exatas e se restringindo somente a casos comuns de geometria da placa e do carregamento. Alguns exemplos em que se têm as soluções exatas são lajes circulares e retangulares simplesmente apoiadas com carregamento uniformemente distribuído. Tal solução foi proposta por Timoshenko e Woinowsky Krieger (1959).
1.2 Objetivo
O objetivo principal do trabalho é apresentar os resultados teóricos estudados pela Teoria das Placas solucionada pela equação diferencial de Lagrange obtendo-se soluções satisfatórias para deslocamentos, momentos positivos e momentos negativos de lajes planas e comparar com os resultados gerados pelo modelagem no SAP2000. Com isso, pretende-se definir uma modelagem adequada e deslocamentos reais, elaborando posteriormente uma análise paramétrica para calcular os valores das flexas após a alteração do fck do concreto e espessura da laje modelada, sendo possível verificar os impactos dessas variações.
1.3 Metodologia
Será utilizada a equação diferencial de Lagrange com resolução matemática pela série de Fourier. Uma vez que a equação diferencial a ser resolvida é de quarta ordem, são necessárias duas condições de contorno, em deslocamentos e/ou esforços internos, para cada parte do contorno da placa. As condições de contorno podem ser geométricas, mecânicas ou mistas. Neste caso será utilizado a solução de contorno de Navier, chamada de solução forçada das equações diferenciais, uma vez que “forçosamente” transforma a equação diferencial em uma equação algébrica, facilitando, consideravelmente, as operações matemáticas necessárias.
Será utilizado também o Software SAP2000 para comparar os resultados modelados com os numéricos que foram calculados pela equação diferencial de Lagrange e a análise paramétrica.
1.4 Caso estudado
Para o presente trabalho, será adotada uma “laje de referência” para o estudo dos esforços e deslocamentos. A adoção de uma laje de referência teve como objetivo aplicar diversos parâmetros a um mesmo caso, com as mesmas condições de contorno, carregamento, de modo que os resultados obtidos pudessem ser comparados entre si.
Foi adotada inicialmente uma laje plana de concreto armado com espessura de 20 cm e dimensão de 10×10 metros, considerando elementos rígidos no contorno com seção de 15x50cm e sem vigas internas. O termo rígido refere-se a elementos que apresentam pouca ou nenhuma deformação, o que é o caso das nossas vigas de borda, com uma ordem de L/200.
A planta baixa de forma da laje estudada apresenta-se na Figura 3.
Para o cálculo da placa através da Teoria das Placas no Regime Elástico, é necessário conhecer o valor da rigidez da placa D, definida em função do módulo de elasticidade do concreto E, da espessura da placa h e do coeficiente de Poisson v (equação 1).

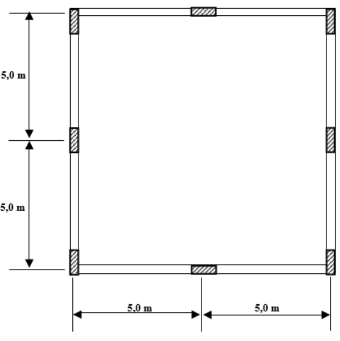
Figura 3 – Planta baixa de forma.
Para resolução do problema, foi adotado apenas um carregamento vertical, sendo desconsiderada quaisquer cargas horizontais. A carga total atuante sobre a laje foi definida como uma carga distribuída de 10 kN/m², simulando a atuação de todas as cargas – peso próprio, revestimento e cargas acidentais. No modelo computacional elaborado com o auxílio do Software SAP2000, será aplicada apenas a sobrecarga proveniente do revestimento e cargas acidentais, pois o peso próprio já é calculado com a definição da geometria e determinação do material.
As propriedades mecânicas do concreto de interesse para o presente estudo são: resistência característica à compressão – fck, o módulo de elasticidade do concreto (E), o módulo de deformação ao cisalhamento G e o coeficiente de Poisson v. Tais parâmetros estão definidos na Tabela 1, incluindo inclusive a rigidez da placa D.
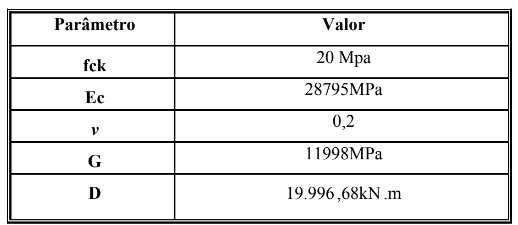
Tabela 1 – Propriedades mecânicas do concreto.
2. Desenvolvimento da equação Lagrange.
A Equação (2) é a equação de Sophie Germain-Lagrange ou Equação Fundamental das Placas. Sua solução é a função w, a qual oferece o deslocamento vertical em relação à posição original para quaisquer pontos (x, y) que estejam sobre o plano médio da placa, antes de sofrerem a ação da carga.
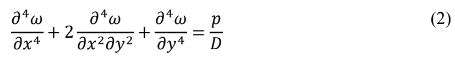
A equação também pode ser escrita na forma Laplaciana:
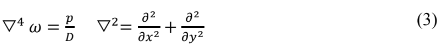
Na análise de uma placa , uma carga p(x,y) qualquer pode ser desenvolvida através de uma série de Fourier infinita em termos de senos conforme a seguinte expressão:
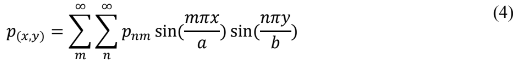
Para Solução da equação (4) será utilizado a solução ou Método de Navier. Navier apresentou a solução de flexão de chapas retangulares simplesmente apoiadas por séries trigonométricas duplas. A solução de Navier é, às vezes, chamada de solução forçada das equações diferenciais, uma vez que forçosamente transforma a equação diferencial em uma equação algébrica, facilitando, consideravelmente, as operações matemáticas necessárias.
As condições de contorno para uma placa simplesmente apoiada são:
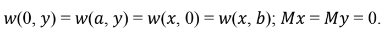
Considera-se uma placa retangular simplesmente apoiada ao longo do contorno exterior e submetida à ação de uma carga distribuída, p(x, y), a qual se pode representar através de Séries Trigonométricas Duplas de Fourier do seguinte modo:
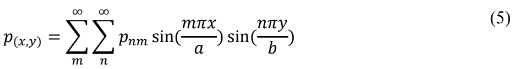
onde Pnm representa a carga, a e b as dimensões da placa. Para calcular o coeficiente
particular Pnm das Séries de Fourier, multiplicam-se ambos os lados da equação por sin(n′πy/b)dy e integra-se de 0 a b.
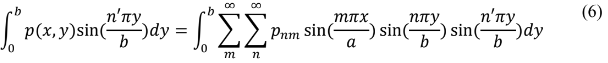
Empregando-se as relações de ortogonalidade:
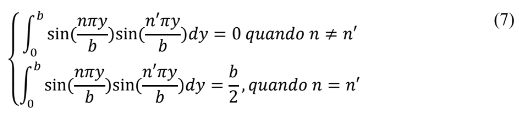
Dessa forma:
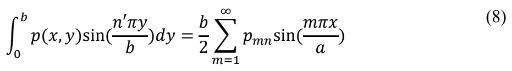
Multiplicando ambos os lados da equação (7) e integrando de 0 a a:
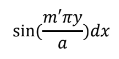
Temos:
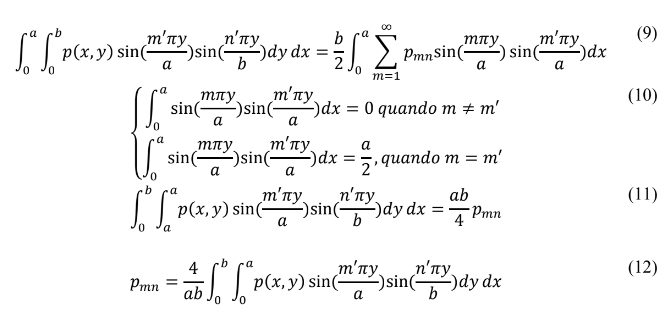
Do mesmo modo que p(x,y) é representado por séries Duplas e Fourier na equação (5) a flexão da placa ω(x,y) e é dada por:
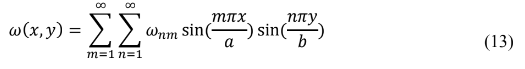
Substituindo na equação (13) na equação diferencial de Lagrange (2), temos:
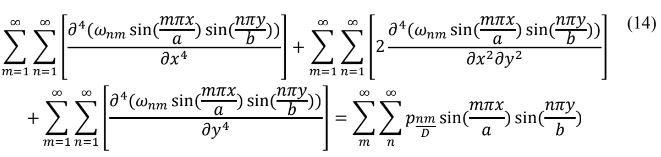
Assim calculando as derivadas parciais de quarta ordem em relação a x, y:
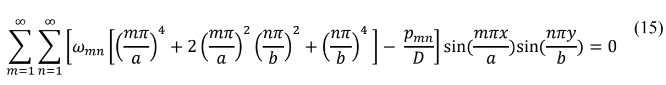
Dessa forma obtém -se :
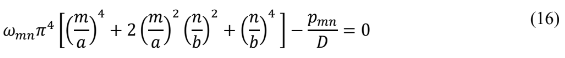
Logo:
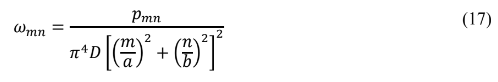
Logo:
Considerando p(x,y) =p0 , Então podemos definir:
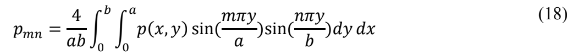
Resolvendo a integral em dx e dy.
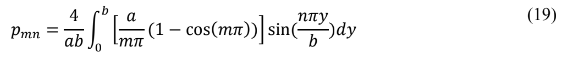
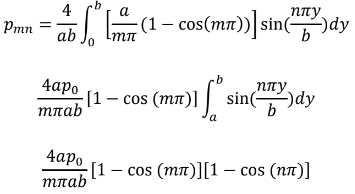
Logo:
Empregando as relações: cos(mπ) = (−1)m e cos(nπ) = (−1)n
Nota -se que para valores pares de m e n os resultados anula-se . Logo n,m são para números ímpares.

Para m, n impares, e substituindo Pmn na equação (13) temos:
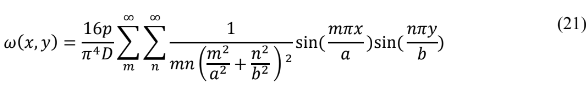
É uma equação válida para calcular placas apoiadas sujeitas a um carregamento Pmn. De formula análoga, obtemos as expressões para os momentos fletores Mx e My.
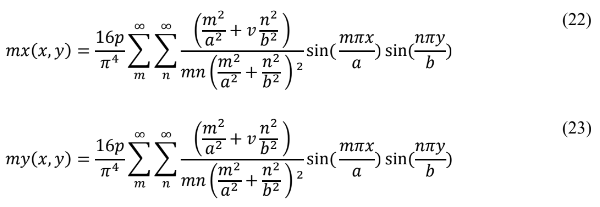
3. Resultados:
Momentos Fletores Mx e My estão apresentados na Tabela 2 e Gráfico 1.
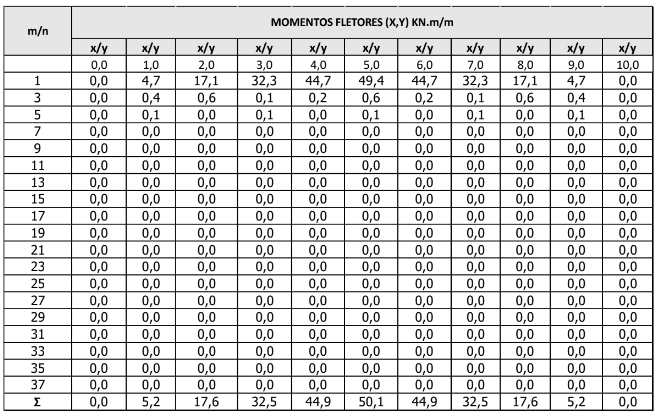
Tabela 2 – Momentos fletores atuantes na laje.
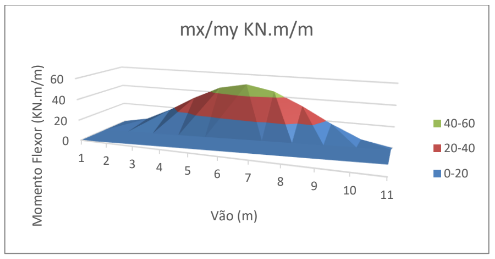
Gráfico 1 – Gráfico dos momentos fletores atuantes.
Deslocamentos verticais estão apresentados na Tabela 3 e no Gráfico 2.
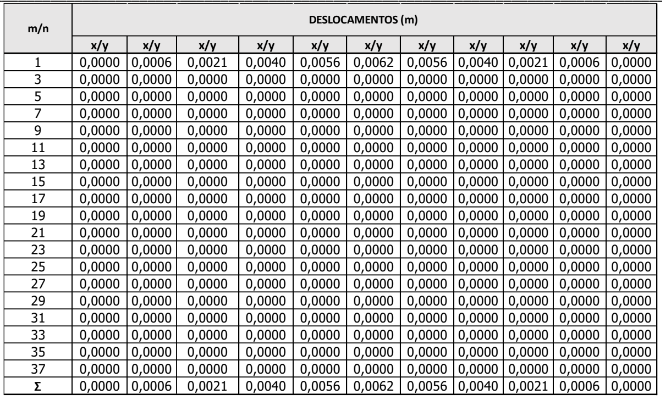
Tabela 3 – Deslocamento da laje.
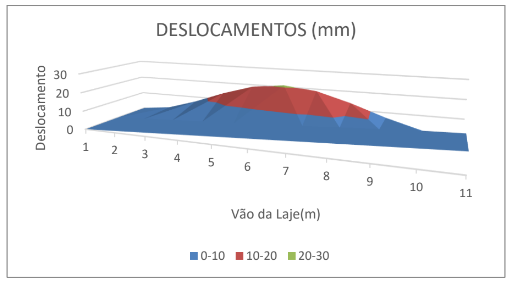
Gráfico 2 – Gráfico dos deslocamentos.
Com o intuito de analisar a influência da variação da resistência do concreto (fck) na deflexão da estrutura, foi elaborada uma análise paramétrica para comparar esses efeitos.
As tabelas 4 e 5 e os Gráfico 3 e 4 apresentam resultados da deflexão no vão da laje em função da variação do fck do concreto, mantendo fixo a espessura da laje de 20 cm para um vão máximo de 10 m.
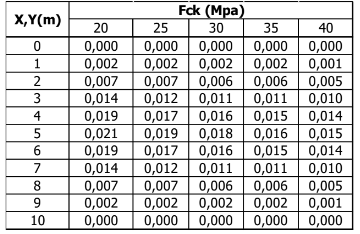
Tabela 4 – Deslocamento pela variação de fck.
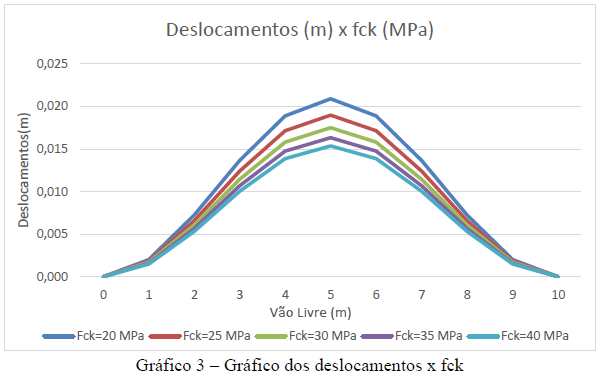
Resultando das deflexões (m) na laje com vão de 10,0 m mantendo o Fck constante de 20Mpa variando somente a espessura da laje.
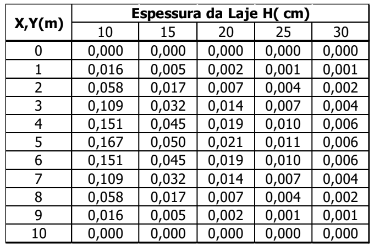
Tabela 5 – Deslocamento pela variação da espessura da laje.
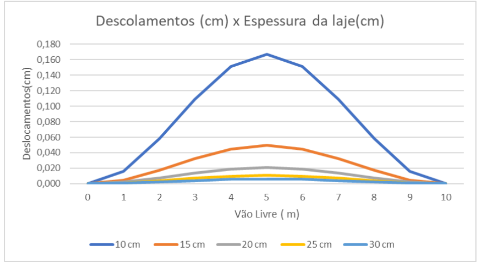
Gráfico 4 – Gráfico dos deslocamentos x espessura da laje.
4. Modelo Computacional:
Com o intuito de simular o comportamento da laje pelo método dos elementos finitos e comparar com os valores dos momentos e deslocamento pelos métodos matemáticos, foi elaborado um modelo computacional pelo Software SAP2000.

Figura 4 – Modelo computacional no Software SAP2000.
O modelo computacional foi elaborado simulando uma laje de 20cm de espessura e com os mesmos parâmetros considerados nas análises matemáticas, sendo assim, temos os seguintes resultados:
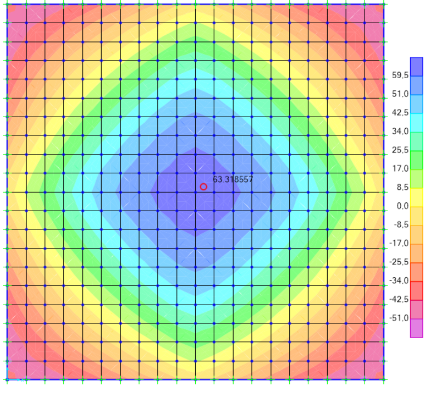
Figura 5 – Envoltória de momento atuante na laje.
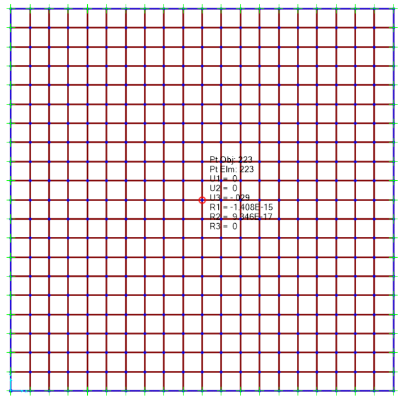
Figura 6 – Deslocamento no centro da laje (d=2,9cm).
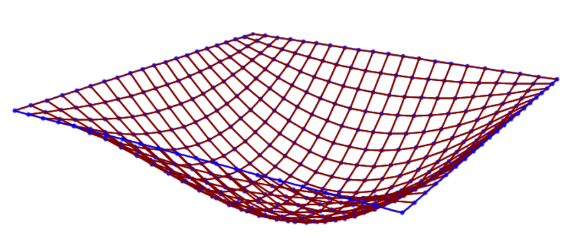
Figura 7 – Deslocamento da laje.
Observa-se que os valores foram muito similares aos elaborados pelos métodos matemáticos.
5. Considerações finais
Os resultados do presente trabalho demonstram a eficácia da utilização da equação de Lagrange solucionada pela Séries de Fourier Dupla no cálculo de elementos estruturais, sendo possível encontrar a deflexão correspondente em qualquer ponto da Laje nas duas direções, bem como seus momentos fletores, mostrando assim, a eficácia dos cálculos realizados.
Também foi possível constatar pela análise paramétrica, que a espessura da laje tem influência representativa na deflexão de lajes, bem como a resistência característica do concreto. Quanto à modelagem com o auxílio do Software SAP2000, pelo método dos elementos finitos, observou-se que os resultados elaborados por metodologias de cálculo apresentaram valores similares ao do modelo computacional.
Referências Bibliográficas
HENNRICHS, Carlos Alexandre. Estudo sobre a modelagem de lajes planas de concreto armado. 2003. Dissertação (Mestrado em Engenharia Civil)-Universidade Federal de Santa Catarina, Santa Catarina. 2003.
DIAS, Nickolas Leitão. A Teoria da Flexão de Placas envolvendo a Equação Diferencial de Lagrange. 2019.f.89 Trabalho de Conclusão de Curso – Curso de Matemática Aplicada- Universidade Federal do Rio Grande do Sul.Rio Grande do Sul. 2019.
DUTRA, Daniel Tanure Franco. Análise de vibrações na deflexão de elementos estruturais de concreto. 2019.Dissertação (Mestrado em engenharia Civil) – Universidade Federal dos Vales do Jequitinhonha e Mucuri. Teófilo Otoni, MG. 2009.
