REGISTRO DOI: 10.5281/zenodo.8363825
Gustavo Saraiva da Silva
Resumo:
O ajuste de modelos de séries temporais são importantes quando se quer entender o comportamento de variáveis ao longo do tempo, além de entender fazer previsões. Assim apresenta-se modelos que tentam explicar a série temporal mensal do Valor de Mercado da Bolsa de Valores de São Paulo registrados de janeiro de 1998 a fevereiro de 2018. Os dados e o modelo ajustado foi analisado com auxílio do software R.
Palavras-chave: BM&FBOVESPA, SARIMA, Holt-Winters.
1 Introdução
A Bolsa de Valores de São Paulo é uma das maiores empresas de serviços financeiros da América Latina e uma das maiores bolsas do mundo em valor de mercado. Valor de mercado é o valor das empresas emissoras de ações integrantes da carteira teórica dos índices. Esse valor é apurado pelo resultado da multiplicação da quantidade de cada tipo/classe de ação de emissão da empresa pela sua respectiva cotação de mercado.
O valor de mercado das empresas oscila ao longo do tempo e depende de inúmeras variáveis aleatórias que interferem na dinâmica do mercado financeiro constantemente, obviamente essa oscilação ocorre também com o valor de mercado da Bmf&Bovespa. Esse comportamento aleatório ao longo do tempo pode ser modelado usando técnicas de análises de séries temporais, por exemplo os Modelos Autorregressivo Integrado de Médias Móveis (ARIMA). Quando a série possui sazonalidade temos um Modelo Autorregressivo de Integrado de Médias Móveis Sazonais. Para dados econômicos, normalmente, temos séries não estacionárias, onde os erros observados são auto correlacionados. Para modelar estes casos, os modelos ARIMA são úteis para os propósitos que temos (MORETIN; TOLOI, 2006).
Popularmente conhecida como metodologia Box-Jeinkis (BJ), umas das técnicas mais usadas, mas tecnicamente como metodologia ARIMA, a ênfase desses métodos não está na construção de modelos uni equacionais ou de equações simultâneas, no entanto na análise probabilística, ou estocástica, das propriedades da própria série temporal econômica sob a filosofia deixe os dados falarem por si mesmos (GUJARATI; PORTER, 2011). Quando a série apresenta maior grau de complexidade pode-se usar a suavização exponencial de Holt-Winters. Assim sendo, o objetivo deste trabalho é estruturar um modelo de série temporal que nos permita analisar com consistência o crescimento do valor de mercado da Bolsa de Valores de São Paulo nos últimos anos.
2 Materiais e Métodos
Os números sobre o valor de mercado da BOVESPA foram obtidos diretamente no endereço eletrônico da Bmf&Bovespa, são os valores medidos mensalmente do valor de mercado em trilhões de reais, no período de Janeiro de 1998 a Fevereiro de 2018, totalizando 242 observações. Os pacotes TSA e tseries do software R foram usados para analisar o banco de dados e estruturar e validar o modelo para a série temporal.
Dizemos que uma série temporal Yt segue um modelo Autorregressivo Integrado de Médias Móveis se a diferençaWt = 5dYt for um processo ARMA estacionário. Se WT segue um ARMA(p,q), dizemos que Yt é um processo ARIMA(p,d,q) (CRYER; KELLET, 1991). O número de diferenças, d, necessárias para que o processo se torne estacionário, é alcançado quando a FAC (Função de autocorrelação) amostral de Wt = 5dZt decresce rapidamente para zero (MORETIIN; TOLOI, 2006). A FAC, ρj , é estimada por
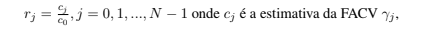

onde φ(B) = 1 − φ1B − φ2B2 − … − φp + dBp+d. Zt faz o papel de Yt da definição de Cryer e Kellet. Para identificar a estacionaridade da série utilizamos o teste de Dickey-Fuller, para maiores detalhes veja (MORETTIN e TOLOI, 2006).
Quando {Zt} exibe um comportamento sazonal determinístico com período 12, um modelo que pode ser útil é Zt = μt + Nt, onde μt é uma função determinística periódica, satisfazendo μt − μt−12 = 0 ou (1 − B12μt = 0) e Nt é um processo estacionário que pode ser modelado por um ARMA(p,q)(MORETTIN e TOLOI, 2006).
Ainda segundo Morettin e Toloi (2006), a identificação dos modelos é feita em dois passos: obter as estimativas preliminares dos parâmetros e calcular os resíduos para examinar as funções de autocorrela ção e autocorrelação parcial. A estimação de máxima verossimilhança dos parâmetros pode ser obtida. As previsões de valores futuros Zt+h são obtidas com Zt(h) = µt+h + Nt(h). Quando µt for um processo estocástico satisfazendo (1−B12µt = Yt), em que Yt é um processo estacionário, o modelo possui sazonalidade estocástica. O modelo
φ(B)Φ(B12)(1 − B12)D(1 − B)dZt = θ(B)Θ12at (3)
é um ARIMA sazonal multiplicativo (SARIMA) de ordem (p, d, q)x(P, D, Q)12. Para a escolha do modelo usa-se o critério de Informação de Akaike AIC = 2 log Lˆ + 2(p + q), em que Lˆ é o valor da máxima verossimilhança, o critério de Informação de Akaike Corrigido AICC =
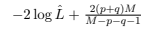
e o Critério de Informação Bayesiano BIC = −2 log Lˆ + (p + q) log M. Para validar o modelo pode-se usar o teste de Ljung e Box (1978). Se o modelo for apropriado a estatística
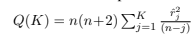
terá aproximadamente uma distribuição χ2 com K-p-q graus de liberdade.
Para séries temporais que apresentam um padrão de comportamento mais complexo, quando a série apresenta mudança de nível, sazonalidade e tendência, pode-se aplicar a suavização exponencial de Holt-Winters (HW). Segundo Morettin e Toloi (2006),existem dois tipos de procedimentos cuja utilização depende das características da série considerada. Em uma série sazonal a variante mais usual do método HW considera o fator sazonal Ft como sendo multiplicativo, enquanto que a tendência permanece aditiva, isto é, Zt = μtFt + Tt + at, t = 1, …, N (MORETTIN; TOLOI, 2006). As três equações de suavização são dadas por
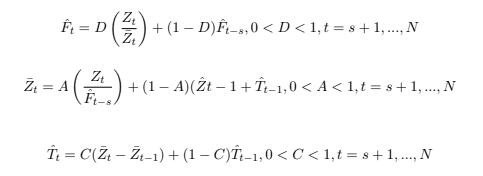

equação (3) é ótima se Zt for gerada por um processo ARIMA sazonal.
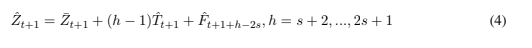
3 Resultados e Discussões
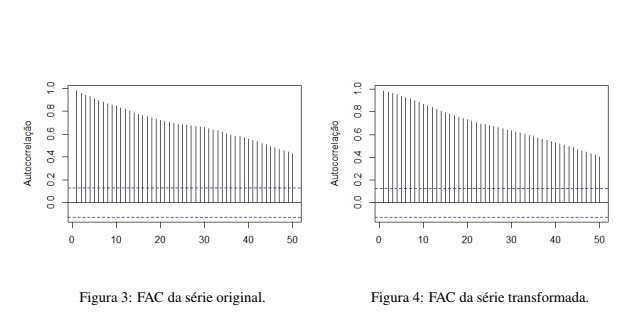
Os valores originais para o valor de mercado da BM&FBOVESPA nos dá uma série temporal não estacionária conforme atestado pelo teste de Dickey-Fuller, valor p = 0, 3746. Na Figura 1, pode-se ver a série temporal para os valores mensais do valor de mercado da BM&FBOVESPA no período de Janeiro de 1998 a Fevereiro de 2018. Observa-se também que há oscilações na variância da série, a primeira metade da série se comporta de maneira mais suave ao longo do tempo quando comparada com a segunda metade da série. Na Figura 3 ver-se que a autocorrelação não converge rapidamente para zero ao longo dos lags, indicando a não estacionaridade da série original.
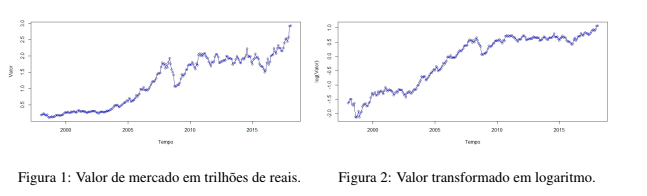
Aplicando-se a transformação logarítmica, na tentativa de minimizar a variância da série, a mesma permanece não estacionária, observa-se novamente o comportamento crescente ao longo do tempo da série transformada Figura 2, a função de auto correlação na Figura 4 e o teste Dickey-Fuller, com o valor p = 0, 757.
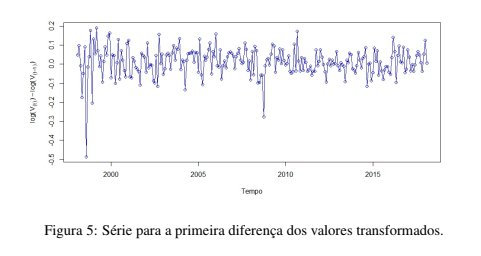
Quando aplica-se a primeira diferenciação na série dos dados transformados, obtém-se a estacionaridade. O teste Dickey-Fuller apontou valor p = 0, 01 para a primeira diferença do logaritmo dos valores de mercado. A série transformada e diferenciada pode ser vista na Figura 5. Os valores da série encontra-se dispersos sem que haja um claro padrão de crescimento ou decrescimento. O teste Run, valor p = 0, 163 com 107 runs observados, aponta aleatoriedade dos valores para esta série.
Nas Figuras 6 e 7 tem-se a visão da função de autocorrelação e da função de autocorrelação parcial para a primeira diferença da série transformada, respectivamente. Nota-se que a há indício de estabilidade, os valores das autocorrelações nos lags não ultrapassaram os limites aceitáveis, com exceção de dois valores na FAC, mas não é visível o padrão de ligeira convergência para zero a medida que o lag
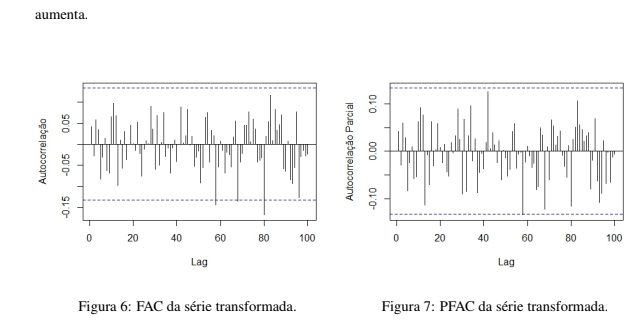
Fazendo-se a decomposição da série transformada, pode-se averiguar melhor as características dos dados. Na Figura 8 observa-se novamente o comportamento da série transformada, crescente ao longo do tempo e com a presença de sazonalidade.
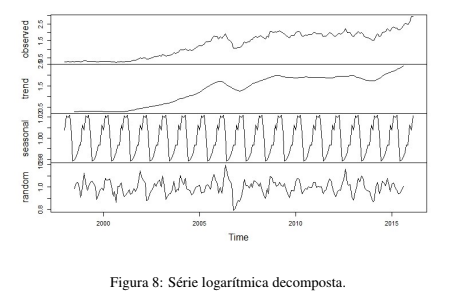
Com o objetivo de minimizar o efeito da sazonalidade na série faz-se a primeira diferença sazonal. Feito isto, o comportamento da série diferenciada sazonalmente pode ser visto na figura 9. Os valores das autocorrelações e das autocorrelações parciais nos lags podem ser vistos nas figuras 10 e 11, respectivamente. O ACF mostra que não há convergência rápida da autocorrelação para zero. O PACF mostra convergência rápida, o que é esperado. O teste Dickey-Fuller que avalia a estacionaridade mostra que a série com a diferença sazonal é estacionária, valor p = 0, 01.
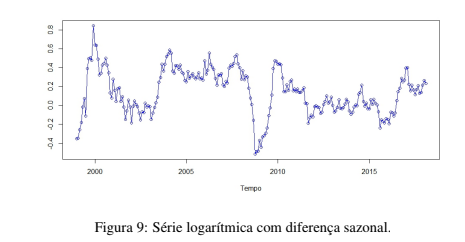
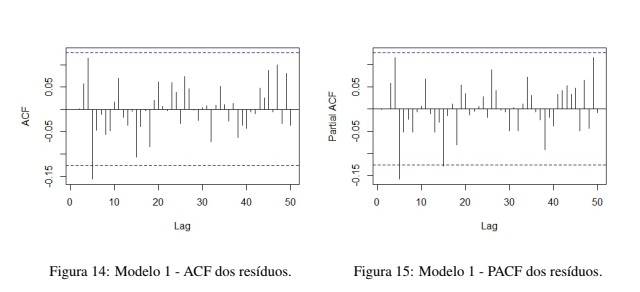
As estimativas dos modelos são dadas pelo método da Máxima Verossimilhança. Aqui verifica-se os cinco modelos com melhores índices de ajustes e menores erros de previsão. Levou-se em consideração o AIC, AICC e BIC como critério de verificação de adequação do modelo aos dados. O primeiro, o modelo SARIMA(2, 1, 2)x(2, 0, 1)12 tem os coeficientes mostrados na Tabela 1. As disposições dos resíduos quanto a condição de normalidade pode ser observadas nas Figuras 12 e 13. O teste de ShapiroWilk atesta a não normalidade dos resíduos do Modelo 1, com W = 0, 92101 e valor p = 4, 756e − 10. As autocorrelações dos resíduos do Modelo 1 pode ser vistas nas figuras 14 e 15. Apenas em um lag o valor da autocorrelação apresenta significância, nos primeiros lags é zero porém nos demais lags essa correlação volta a crescer, embora tenham todas valores pequenos. Também verifica-se que a correlação não tem comportamento tendendo para zero a medida que o número de lag aumenta.
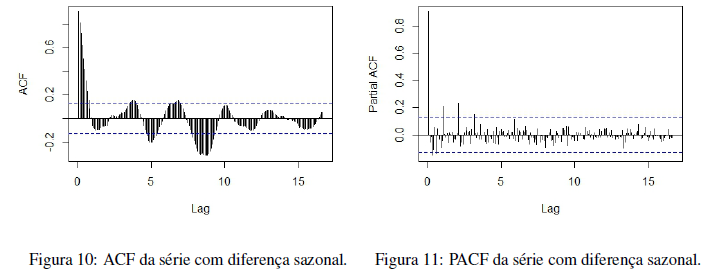
Tabela 1: Modelo 1 – SARIMA(2, 1, 2)x(2, 0, 1)12
Coeficientes ar1 ar2 ma1 ma2 sar1 sar2 sma1 drift Estimativa -0,0048 -0,0045 0,0015 0,0009 -0,2638 -0,1311 0,3354 0,0110 S.E. 0,0890 0,4305 NaN 0,3809 0,5159 0,0984 0,5179 0,0046 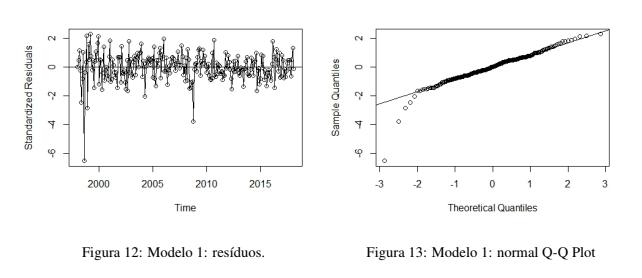
Os resíduos do Modelo 1 têm correlações insignificantes nos lags, porém os valores residuais não
encontram-se normalmente distribuídos. Nessas condições, não podemos dizer que o Modelo 1 possa
nos repassar as informações da série de valor de mercado da BM&FBOVESPA.
Uma outra alternativa é o Modelo 2 com os coeficientes descritos na Tabela 2. Para este segundo
modelo os resíduos também não estão distribuídos normalmente, segundo o teste de Shapiro-Wilk, com
W = 0, 93604 e valor p = 9, 175e − 09, a hipótese de normalidade foi afastada. O ACF e o PACF dos resíduos do Modelo 2, que pode ser observado nas Figuras 18 e 19 respectivamente, indicam comportamento semelhante aos resíduos do Modelo 1. O teste de Ljung-Box também não atestou o Modelo 2 como sendo válido para descrever o valor de mercado da BM&FBOVESPA ao longo dos anos. O resultado do teste Ljung-Box para os modelos pode ser observado na Figura 20.
Tabela 2: Modelo 2: SARIMA(2, 1, 3)x(2, 0, 1)12
Coeficientes ar1 ar2 ma1 ma2 ma3 sar1 sar2 sma1 drift Estimativa 1,3178 -0,8768 -1,3491 0,9603 0,0021 -0,1384 -0,1407 0,1775 0,0110 S.E. 0,0599 0,0867 0,0940 0,1214 0,0815 0,6775 0,0884 0,6840 0,0048
A Tabela 3 mostra os valores dos coeficientes que mostra a bondade do ajuste. O Segundo modelo é
apontado como o melhor, pois têm os menores coeficientes AIC, AICc e BIC.
Tabela 3: AIC, AICC e BIC dos modelos.
Modelo AIC AICc BIC SARIMA(2, 1, 2)x(2, 0, 1)12 -553,11 -552,33 -521,75 SARIMA(2, 1, 3)x(2, 0, 1)12 -559,41 -558,46 -524,57
As tabelas 4, 5 e 6 mostra os erros das previsões dos modelos estimadas para os meses de março,
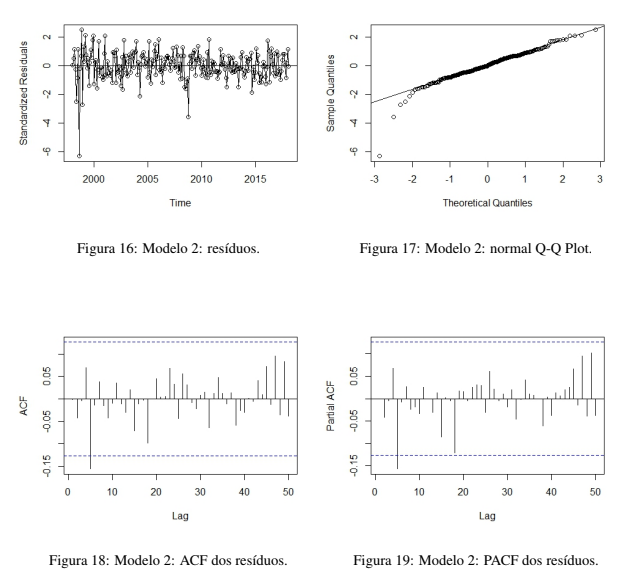
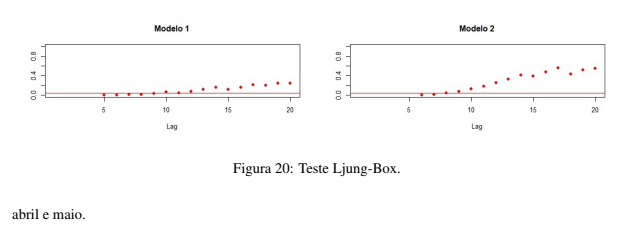
Tabela 4: Erro de previsão para o mês de março
Modelo Erro SARIMA(2, 1, 2)x(2, 0, 1)12 -209,1838 SARIMA(2, 1, 3)x(2, 0, 1)12 -209,189
Tabela 5: Erro de previsão para o mês de abril
Modelo Erro SARIMA(2, 1, 2)x(2, 0, 1)12 -210,8205 SARIMA(2, 1, 3)x(2, 0, 1)12 -210,861
Tabela 6: Erro de previsão para o mês de maio
Modelo Erro SARIMA(2, 1, 2)x(2, 0, 1)12 -245,822 SARIMA(2, 1, 3)x(2, 0, 1)12 -245,8222
A suavização exponencial de Holt-Winters foi bastante precisa para nossos dados. Na Tabela 7 pode-se ver as estimativas para os meses de março abril e maio. Na Figura 21 observa-se o comportamento da série observada, em preto, e da série estimada, em vermelho.
Tabela 7: Previsões Holt-Winters.
Março Abril Maio Holt-Winters Aditivo 28,73288 28,75528 28,68734 Holt-Winters Multiplicativo 28,73549 28,75983 28,69075 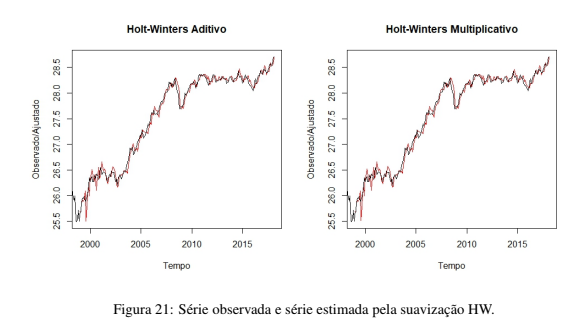
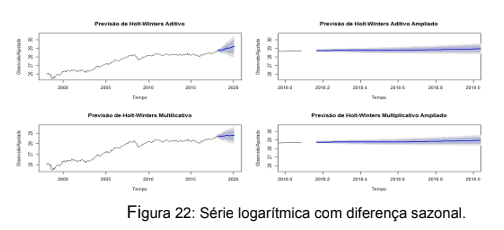
Na Figura 22 tem-se a estimativa de previsão para a série. Como observa-se, a previsão para os
próximos meses é de leve crescimento para o valor de mercado da BM&FBOVESPA.
4 Considerações Finais
Após o estudo da análise de séries temporais, podemos perceber a grande importância dos modelos de séries temporais, pois nos deparamos com Modelos Sazonais de Box e Jinks e Suavização Exponencial Aplicado ao Valor de Mercado da BM&FBOVESPA, com isso a técnica dos modelos de séries temporais e dos modelos SARIMA são possíveis escolhas.
No trabalho utilizou-se o método de análise de séries temporais, mas também com ajuda no programa computacional R, as previsões para a bolsa foram bastante satisfatórias, assim a estimativa de previsão para a série. Como observa-se, a previsão para os próximos meses é de leve crescimento para o valor de mercado da BM&FBOVESPA.
Referências
CRYER, Jonathan D.; KELLET, Natalie. Time series analysis. Royal Victorian Institute for the Blind. Tertiary Resource Service, 1991.
GUJARATI, Damodar N.; PORTER, Dawn C. Econometria Básica-5. Amgh Editora, 2011.
HURVICH, Clifford M.; TSAI, Chih-Ling. Regression and time series model selection in small samples. Biometrika, v. 76, n. 2, p. 297-307, 1989.
MORETTIN, Pedro A.; TOLOI, Clélia. Análise de séries temporais. In: Análise de séries temporais. 2006.
SCHWARS, G.et al. Estimating the dimension of a model. The annals of statistics, institute of Mathematical Statistics, v. 6, n. 2, p. 460 – 464, 1978.
