REGISTRO DOI: 10.5281/zenodo.7942482
Cleuber Silva1
Resumo. Este texto tem o intuito de apresentar uma proposta de solução para o problema de distribuição de temperatura no disco. Para tanto, é apresentada solução através do método de separação de variáveis por coordenadas polares complementando com o Software Mathematica modela-se o problema com respeito a algumas condições iniciais propostas.
1. Introdução
O problema da transferência de calor no disco se mostra bastante interessante do ponto de vista matemático, pois além do envolvimento de coordenadas polares, aparecem as funções de Bessel não comuns em problemas de uma placa retangular, por exemplo. O conhecimento do comportamento dessas funções é de extrema importância para a solução deste problema, visto que se ganha tanto a análise quando r ! 0 quanto em relação ao tamanho do disco de raio r = b através dos Zeros de Bessel. Falando especificamente das funções de Bessel, elas são obtidas a partir de uma equação diferencial de segunda ordem do tipo

Desse modo, sob o viés destas funções, pode-se chegar a resultados bastante concretos e com ajuda do Software de álgebra computacional Mathematica, se verá o comportamento de temperatura em cada região do disco bem como as condições iniciais influenciam na sua solução. Utilizando-se de u0(r, θ) = J3(ζ3r) cos(3θ) e u∗0(r, θ) = sin(r) sin(r − 1) cos(3θ) como condições iniciais, obteremos a solução do problema.
2. Situação Problema

Admite-se que este problema não possui fonte interna de calor pode-se dizer que a formulação do problema é dada por:

donde,
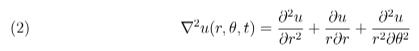
Através desta formulação, pretende-se estudar o comportamento radial de temperatura ao longo do tempo.
3. Metodologia
De posse do método de separação de variáveis pode-se ter,

Podemos escrever a equação 1, da seguinte forma:
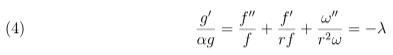
Reescrevendo a equação 4,
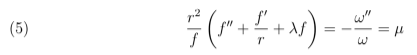
E assim resume-se o problema em resolver o sistema,
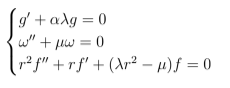
Para a primeira equação, obtém-se a solução geral,

Para que se possa solucionar a segunda equação do sistema, tem-se os seguintes casos:
3.1. Caso 1. µ = 0
Isso implica em:
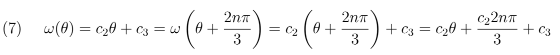
Portanto, c2 = 0 e determina-se,

3.2. Caso 2. µ = β2 > 0
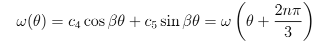
Que equivalente a escrever:
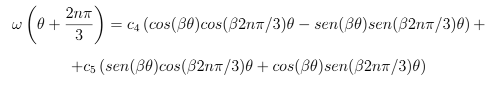
Igualando estas equações, obtém-se
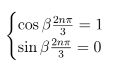
Portanto,
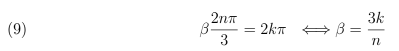
Então:
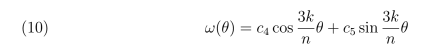
3.3. Caso 3. µ = −β2 < 0, pode-se escrever:
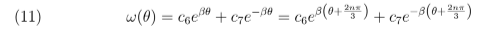
Segue portanto que a equação 11 é válida se β = 0 e assim µ = 0 que é justamente o caso 1, já analisado anteriormente.
Finalmente vamos analisar a terceira equação do sistema com os seguintes casos:
3.4. Caso 4. µ = 0 e λ = 0
A equação se tornará:

Cuja solução geral é dada por:

Tomando r = b tem-se:
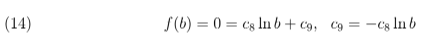
Segue portanto,

3.5. Caso 5. λ = 0 e µ > 0
Portanto a terceira equação do sistema se tornará:

Façamos uma análise da solução usando-se série de potência, definindo-se:

donde as respectivas derivadas são:
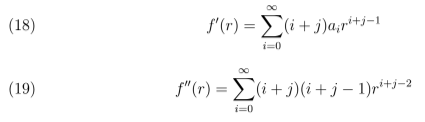
Substituindo as equações 17, 18, 19 em 16 tem-se:
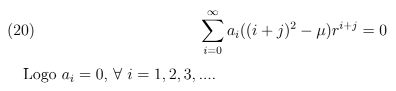
3.6. Caso 6. λ = γ2 > 0 e µ = 0
Cujo solução é dada por:
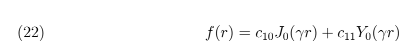
Quando r → 0+ tem-se que Y0(γr) → −∞, logo:

Como f(b) = 0, temos que J0(γb) = 0. Seja xi alguma raiz de J0(γb), tem-se:

A equação 25 se tornará:

3.8. Caso 8. λ = −γ2e µ = 0
Essa análise é análoga ao caso 6. A modificação geral se dá pela equação de Bessel modificada que nós representaremos por In. De fato a solução geral deste caso é dada por:
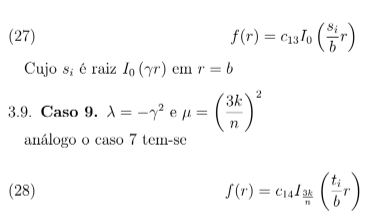
Agora finalmente aglomerando todas as soluções usando-se o fato de u(θ, r, t) = f(r)g(t)ω(θ), temos:
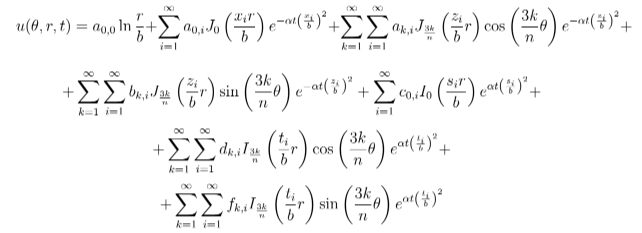
Supondo t = 0 tem-se u(r, θ, 0) = u0(r, θ) Segue que:
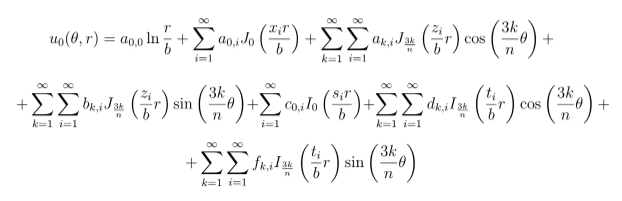
4. Condição u0(r, θ) = J3(ζ3r) cos(3θ)
Dado que u0(r, θ) = J3(ζ3r) cos(3θ) temos que:
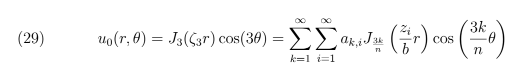
Façamos primeiro o caso n = 1 e fazendo b = 1 a equação 34 se tornará:
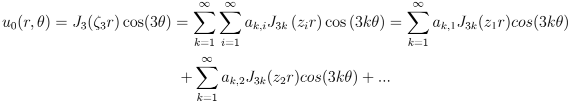
Pela lei de formação de u0(r, θ), toma-se o valor de k = 1 em cada somatório e portanto:
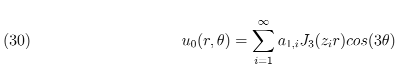
Usando-se a ortogonalidade da função J podemos escrever:
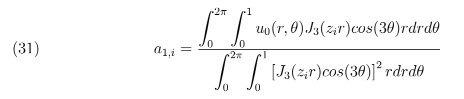
5. Condição u∗0(r, θ) = sin(r) sin(r − b)cos(3θ)
De maneira análoga a seção anterior, tem-se

Usando-se a ortogonalidade da função J pode-se escrever:
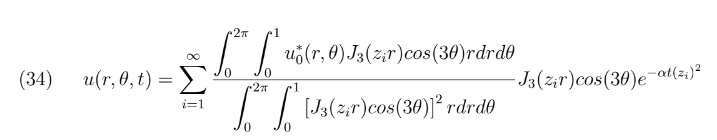
6. Resultados Obtidos
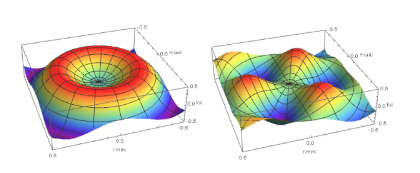
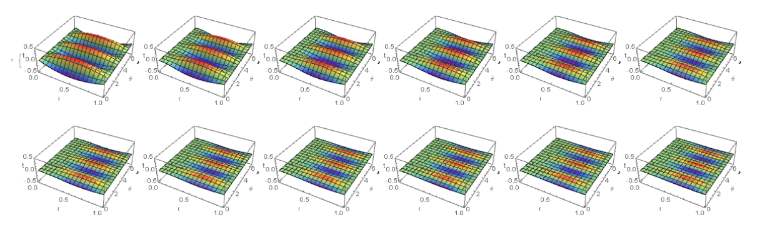
Para uma modelagem computacional deste problema foi utilizado o Software Mathematica tendo como referência o alumínio cuja difusividade térmica α = 98, 8mm2 s. Tomando-se a condição u0(r, θ) = J3(ζ3r) cos(3θ) foram obtidos os resultados mostrados na figura 1:
Figura 1. Evolução do perfil de temperatura da Placa

É importante notar que no instante inicial o perfil de u(r, θ, t) obedece a J3(ζ3r) cos(3θ) é periódico. Dado que u(r, θ, 1) = 0, de certo o perfil de temperatura da placa irá convergir para 0 no regime permanente. É fato que tal resultado diante da boa difusividade térmica do alumínio tem convergência rápida e em pouco tempo como se vê a figura 1.
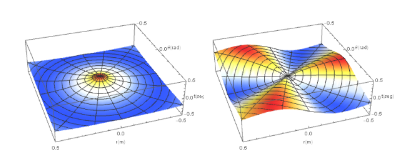
Por outro lado, na figura 2, tem-se respectivos corte do perfil de temperatura no instante inicial para θ = 0, ou seja u(r, 0, 0) e um corte de perfil de temperatura u(r, θ, 0).
Figura 2. Perfis em u(r, 0, 0) e u(r, θ, 0) respectivamente
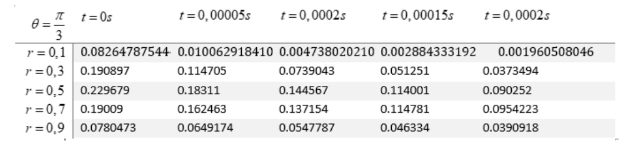
Na figura 3 encontra uma tabela de temperatura para θ = 0. É importante notar a convergência para 0 em todas as análises para diferentes raios sejam eles mais perto do centro ou mais afastados.
Cada resultado mostrado na tabela 4 foi definido para 20 termos da série de u(r, θ, t). Como teste aumentou-se para 40 termos e os resultados continuam convergindo. Isso acontece pelo fato dos coeficientes da série de u serem muito pequenos quando n → ∞ acarretando uma convergência para os valores da tabela.
Figura 3. Tabela de Temperatura do disco em θ = 0
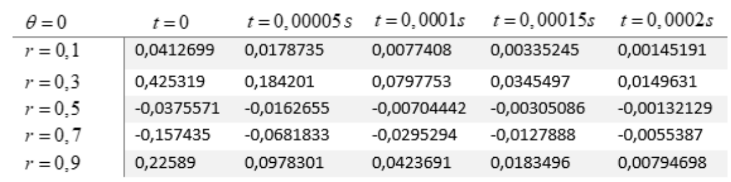
Para a condição u∗0(r, θ) = sin(r) sin(r −1) cos(3θ) a figura 4 tem-se a evolução de temperatura:
Figura 4. Evolução do mapa de Temperatura no tempo
É importante notar que devido a u∗0(r, θ) a mapa de temperatura na evolução temporal entrou em regime permanente em tempo superior ao analisado na seção anterior.
Figura 5. Mapa de Temperatura para u(r, 0, 0) e u(r, θ, 0) respectivamente
Para verificar a convergência de temperatura, toma-se em θ =π3 segundo a figura 6.
Todas as temperaturas calculadas na figura 6 são para os 20 primeiros termos da série de u. Aumentando-se a quantidade de termos para 40, os resultados mostraram uma convergência para os valores desta figura. De fato, cada coeficiente da série converge para 0 e portanto os valores de temperatura convergem para esta tabela.
Figura 6. Evolução da Temperatura no tempo para θ =π3
7. Conclusão
Verifica-se então, que o mapa de temperatura no disco com bordo nulo é bastante influenciado pela função u0(r, θ) dada. De fato, para u0(r, θ) = J3(ζ3r) cos(3θ), a função de Bessel exerce grande influência na convergência mais rápida em comparação a u∗0(r, θ) = sin(r) sin(r − 1) cos(3θ). Com a implementação computacional do problema foi possível verificar que essa convergência mais rápida, foi devido a cada coeficiente da série ser da ordem de 10−16.
No entanto, o alumínio precisa ser citado pelo fato de ter uma alta condutividade térmica. Mesmo com convergência diferente para as condições apontadas no problema, vê-se de fato uma boa convergência para ambos os métodos. Abre-se a possibilidade para trabalhos futuros, comparar convergência de temperatura para diferentes materiais adicionando fonte térmica interna, modificando a solução da EDP original.
8. Referências
1 ZILL, D.G; CULLEN M.R. Matemática Avançada para Engenharia.3.ed. Porto Alegre, Bookman, 2009.
2 DELYRA, JORGE L. Funções de Bessel
cleuber.silva30@gmail.com
