REGISTRO DOI: 10.5281/zenodo.7806817
Yves-Garnard Irilan1
Paul André2
Resumo:
A maioria de nós não está ciente dos usos das estatísticas na vida diária. Existem vários usos de estatísticas na vida diária. A estatística é regularmente usada em estudos médicos para entender como diferentes fatores estão relacionados. Por exemplo, as profissões médicas costumam usar correlação para analisar como fatores como peso, altura, tabagismo, hábitos de exercício e dieta estão relacionados. O principal objetivo deste trabalho é definir a relação da taxa de nascimento de acordo com a idade da mãe com a taxa de mortalidade infantil até os 5 anos de idade e quais os fatores determinantes para as variáveis estarem conectadas.
Abstract
Most of us are not aware of the uses of statistics in daily life. There are many uses of statistics in daily life. Statistics is regularly used in medical studies to understand how different factors are related. For example, the medical professions often use correlation to analyze how factors such as weight, height, smoking, exercise habits and diet are related. The main objective of this work is to define the relationship between the birth rate according to the mother’s age and the infant mortality rate up to 5 years of age and which are the determining factors for the variables to be connected.
INTRODUÇÃO
O campo da estatística preocupa-se com a coleta, análise, interpretação e apresentação de dados. Ao aprender sobre estatística, os alunos geralmente perguntam: quando a estatística é realmente usada na vida real? Acontece que ela é usada em muitos campos diferentes para uma variedade de aplicações. Neste artigo, tratamos uma situação pratica de como a estatística é usada na vida real.
Este trabalho de pesquisa tem por objetivo principal definir a relação da taxa de nascimento de acordo com a idade da mãe com a taxa de mortalidade infantil até os 5 anos de idade e quais os fatores determinantes para as variáveis estarem conectadas. Com base em nossos resultados após os cálculos realizados, entre estes podemos citar a média, variância, desvio padrão, intervalos de confiança e testes de hipótese, incluindo a utilização dos métodos de Bernoulli e Poisson e com a discussão que será apresentada na sequência com todos os integrantes da pesquisa iremos demonstrar como os valores são significativos e de grande relevância para a nossa própria interpretação. Além disso, para se obter maior precisão nos gráficos e cálculos utilizamos o Excel, também iremos conceituar todos os cálculos utilizados usando ilustrações de fórmulas para maior entendimento.
1. METODOLOGIA
Para realização e conclusão do trabalho usamos uma variável aleatória em condições distintas, sendo estas a taxa de nascimento de acordo com a idade da mãe e a taxa de mortalidade infantil até os 5 anos de idade com amostras superiores a 100 dados. Para obtenção dos resultados que serão expostos mais à frente fizemos um planejamento, coletamos os dados que seriam úteis e os classificamos. Essa pesquisa se caracteriza como quantitativa, segundo Bell (2004, p.19-20) os “investigadores quantitativos recolhem os fatos e estudam a relação entre eles”.
1.1 Conceitos básicos
Reconhecemos que a melhor forma para adquirir compreensão e entendimento no decorrer da pesquisa é dar início aos conceitos básicos que nos auxiliarão no processo de esclarecimento de pontos importantes que serão abordados.
Para tanto, a estatística pode ser conceituada como a ciência que se preocupa com a organização e com a descrição, análise e interpretação de dados que são obtidos em amostras ou experimentos. Dentro da conceituação de estatística podemos mencionar dois relevantes conceitos que são o de população e amostra. Respectivamente o primeiro está relacionado com o conjunto de elementos com pelo menos uma característica em comum ou ainda pode ser classificado como o conjunto que inclui todas as observações possíveis, diferentemente de amostra em que é um subconjunto da população, ou seja, esse é selecionado por critérios específicos incluindo uma parte significativa das observações feitas. Além disso, precisamos considerar que a amostragem é caracterizada como um método ou até mesmo uma técnica de uma amostra.
Além disso, variável é qualquer característica que se deseja estudar dentro do conjunto de uma amostra ou população, classificada em dois tipos, qualitativa descrevendo os elementos com palavras, isto é, não é descrita com números, diferentemente da quantitativa.
1.2 Medidas de tendência central
As medidas de tendência central de modo objetivo são as medidas típicas ou representativas de um conjunto de dados, indicando dessa maneira o valor típico ou prevalente de uma distribuição de frequência. Dentro das medidas de tendência central encontramos a média aritmética, moda e mediana e são esses conceitos que abordaremos na sequência, pois, descrevem características dos valores numéricos de um conjunto de observações em torno do que podemos considerar ponto de equilíbrio dos dados.
A média aritmética representa o ponto central de qualquer distribuição, situando-se entre o valor máximo e o valor mínimo, sendo considerada como o valor que pretende ser o resumo de todos os valores encontrados na distribuição. Em seu cálculo faz-se a soma dos valores e divide-se esta pelo número de observações realizados da série. Porém, a média aritmética tem suas desvantagens, ela pode ser influenciada por valores extremos, por conta disso não deve ser utilizada quando a distribuição é muito assimétrica e a média aritmética não permite uma descrição completa.
A média aritmética simples possui uma fórmula e a média aritmética ponderada usada quando se atribui pesos diferentes para os valores possui outra fórmula.
Segundo Larson e Farber (2016):
A média de um conjunto de dados é a soma dos valores dos dados dividida pelo número de observações. Para determinar a média de um conjunto de dados, use uma das fórmulas a seguir.
Média populacional:
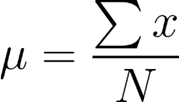
Média amostral:
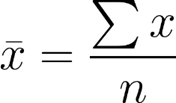
A letra grega minúscula mi representa a média populacional e (lê-se “x” barra) representa a média amostral. Note que N representa o número de observações em uma
A mediana é o valor da variável baseando-se nos dados ordenados anteriormente, posicionando-se exatamente no meio desse conjunto de dados. O seu cálculo necessita de uma organização antecipada em ordem crescente ou decrescente, feito isso, analisar o n.
Se n é ímpar, a posição da mediana é dada por:
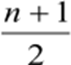
Se n é par, a posição da mediana é dada por:
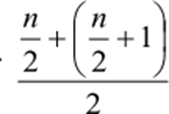
Segundo Crespo (2009):
Dada uma série de valores, de acordo com a definição de mediana, o primeiro passo a ser dado é o da ordenação (crescente ou decrescente) dos valores.
Em seguida, tomamos aquele valor central que apresenta o mesmo número de elementos à direita e à esquerda.
Se, porém, a série dada tiver um número par de termos, a mediana será, por definição, qualquer dos números compreendidos entre os dois valores centrais da série. Convencionou- se utilizar o ponto médio.
Verificamos que, estando ordenados os valores de uma série e sendo n o número de elementos da série, o valor mediano será:

A mediana não é influenciada por valores extremos assim como a média, dispensando cálculos complexos, no entanto, a mediana não utiliza a totalidade dos dados e é um valor posicional, ou seja, não vem definido por uma expressão matemática.
Por último, mas não menos importante temos a moda caracterizada por ser um valor que ocorre com mais frequência, isto é, o valor que mais se repete dentro de todos os dados coletados. No entanto, a moda pode não existir e também pode não ser única.
1.3 Medidas de dispersão ou de variabilidade
Distintivamente das medidas de tendência central, as medidas de dispersão quantificam a variação dos dados em relação à média e qual o seu grau de representatividade, em outras palavras, indicam o quanto as observações se distanciam da média calculada do conjunto e expressam quão dispersos estão os valores da amostra. Para medir essas dispersões que ocorrem se faz necessário a utilização de desvio médio, variância, desvio-padrão, amplitude que iremos apresentar a seguir.
O desvio médio é responsável por analisar a dispersão dos dados conforme a média, isto é, é a média dos valores absolutos dos desvios dos dados em relação ao seu valor central que pode ser considerado geralmente como a média. Para o cálculo primeiramente é realizado somatório das diferenças em módulos de cada um dos valores de um conjunto de informações e sua média aritmética, ou seja, deve-se atentar-se em calcular a média para prosseguir para o desvio médio, logo após dividir o resultado pelo número de informações desse conjunto.
Para dados oriundos de uma população:
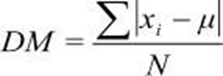
Para dados oriundos de uma amostra:
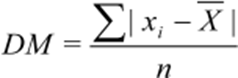
Variância é representada pela média aritmética dos quadrados dos desvios que
foram encontrados anteriormente, matematicamente ela é obtida pela soma das diferenças entre cada elemento da população ou amostra dependendo da sua escolha e sua média elevadas ao quadrado. Quando se trata de uma população utilizamos a2 e para amostras s2. Apresentamos a seguinte fórmula para maior esclarecimento:
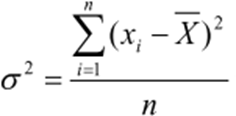
O desvio-padrão por sua vez é uma das medidas de dispersão mais utilizadas, podendo ser definido como uma medida da variação dos valores em torno da média. Como podemos perceber para obtenção dos resultados dos cálculos precisamos seguir uma sequência. No cálculo do desvio-padrão usa a variância, porém, acrescenta-se a raiz quadrada em torno do resultado alcançado. Sua fórmula é expressa de tal forma que tanto a interpretação da variância quanto do desvio-padrão é o mesmo, acrescentando a igualdade do conjunto de dados.
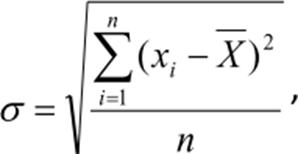
Desvio – padrão da população:
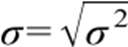
Desvio – padrão da amostra:
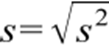
Ressaltando que o valor obtido descreve o maior ou menor grau de dispersão da distribuição referente a média aritmética, isto significa que, quando os dados de uma série foram próximos entre si, não haverá um valor de desvio-padrão grande, este será pequeno, no entanto, quanto maior a diferença, maior o desvio-padrão proporcionalmente.
O coeficiente de variação ou de variação se baseia na comparabilidade do desvio-padrão com a média das distribuições, utilizado quando a intenção de comparar duas ou mais distribuições possuindo médias diferentes estão evidentes. A fórmula é dada da seguinte maneira: Para dados de uma população:
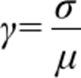
Para amostra:
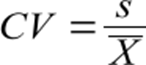
A amplitude é a diferença entre o maior elemento do conjunto e o menor, basicamente precisa-se analisar os elementos que você possui dentro do conjunto e subtrair o maior elemento do menor.
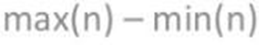
1.4 Histograma
O histograma foi introduzido pela primeira vez por Karl Pearson e consiste em ser um diagrama de colunas representadas graficamente pela função de probabilidades ou função de densidade de um conjunto de dados. Sua representação mais comum é o gráfico de barras verticais, sendo os intervalos de igual magnitude e sua altura diretamente proporcional à frequência, em outras palavras, é composto por retângulos justapostos em que cada base corresponde ao intervalo de classe e sua altura.
1.5 Distribuição de frequência
Pode-se dizer que a distribuição de frequências é um agrupamento de dados em classes, de tal forma que é possível destacar o valor numérico das ocorrências de cada classe, este chamado de frequência absoluta. Nesse aspecto podemos destacar o ROL, tabela obtida após a ordenação dos dados, podendo ser em ordem crescente ou decrescente. A distribuição de frequência sem intervalos de classe é ambígua da
distribuição de frequência com intervalos de classe pelo detalhe que a primeira é a simples condensação dos dados conforme as repetições de seus valores e a segunda necessita o agrupamento dos valores em vários intervalos por conta do tamanho da amostra ser elevado.
1.5.1 Elementos da distribuição de frequência
A elaboração de uma tabela de frequência exige conhecimentos básicos, mas que precisam ser lembrados, entre estes estão a marca de classe, frequência, limites de classes, amplitude dos intervalos, total e ponto médio.
Classe ou marcas de classe são valores individuais, os intervalos de variação da variável, simbolizada por i, enquanto o número total de classes é simbolizado pela letra k.
A frequência representada pela letra (f) é a segunda coluna e representa o número de vezes por exemplo que o dado do intervalo ocorre com base no rol elaborado, destacando que o somatório de todas as frequências é igual ao número total de observações.
Os limites de classe são os extremos de cada intervalo de classe, o limite inferior é o menor número e o limite superior maior número.
A amplitude de um intervalo de classe como o próprio nome já diz é o intervalo que define a classe, obtida através da diferença do limite superior e inferior. E o ponto médio é a média aritmética entre o limite superior e o limite inferior de cada classe.
Além disso, precisamos mencionar a regra de Sturges que é um critério para determinar o número de classes ou intervalos necessários, seu valor corresponde a 1 somado a 3,3 multiplicado pelo logaritmo do total de dados.
1.5.2 Tipos de frequências
Agora que explicamos os elementos podemos passar para os tipos de frequência, como já havíamos mencionado a frequência absoluta é o número de observações correspondente a cada classe.
A frequência relativa é o quociente entre a frequência absoluta da classe correspondente e a soma das frequências, ou seja, o total observado, por outro lado
a frequência percentual apenas será obtida após a multiplicação relativa por 100% e a frequência acumulada é o total, no caso a soma de todas as classes anteriores até a classe atual.
1.6 Intervalo de confiança
O intervalo de confiança pode ser definido como uma medida de imprecisão utilizando-se em casos que o parâmetro é desconhecido, indicando a confiabilidade de uma estimativa.
A intenção é construir um intervalo de confiança para o parâmetro com uma probabilidade de 1 – α, este indicado como o nível de confiança, para que o intervalo contenha o verdadeiro parâmetro, em que α é o nível de significância, ou seja, o erro que estaremos cometendo ao afirmar qualquer suposição. Adotamos a regra de que zp significa também o valor da variável aleatória Z, em outras palavras, a área sob a curva normal padrão à esquerda de zp é igual a p.
Além disso, vale destacar que para qualquer estudo não é possível garantir que o intervalo de confiança contenha o parâmetro real da população.
1.6.1 Notações importantes
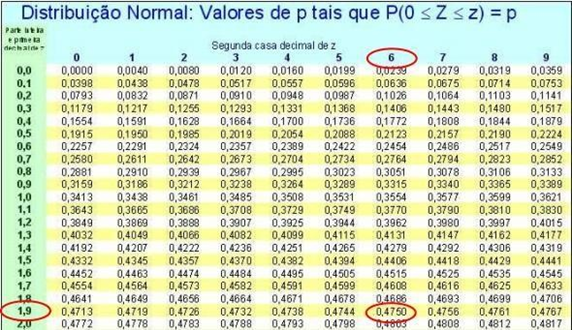
Para efetuar os cálculos é necessário atentar-se a tabela com todos os valores distribuídos e organizados que veremos logo a seguir, no exemplo demarcado na tabela de modo que o valor do intervalo de confiança foi definido como 95% e encontrado o valor de 0,4750.
Tabela 1 – Valores para distribuição em intervalo de confiança
1.7 Testes de hipótese
O teste de hipótese utiliza uma técnica para se obter a inferência estatística, isto é, com o base nos dados amostrais, o teste de hipótese pode inferir-se sobre a população, formulando-se uma hipótese quanto ao valor do parâmetro populacional e pelos elementos amostrais tem-se uma aceitação ou rejeição, dissemelhantemente do que ocorre com a inferência através de intervalo de confiança, nesse caso busca- se o parâmetro populacional desconhecido, cercando-o.
De acordo com Luis Felipe Dias Lopes com as hipóteses estatísticas são consideradas suposições quanto ao valor de um parâmetro populacional ou quanto à natureza da distribuição de uma variável populacional.
Seguidamente, temos tipos de hipóteses, entre estas estão a hipótese nula expressando uma igualdade e hipótese alternativa que é uma desigualdade. Nesse aspecto podemos expor os dois tipos de erros ao testar uma hipótese estatística, pode ser que ao rejeitar uma hipótese ela seja de fato verdadeira ou pode ocorrer de aceitar uma hipótese e ela ser falsa, essa rejeição de uma hipótese verdadeira é conhecida como “erro tipo I” e a hipótese falsa identificada como “erro tipo II”.
1.8 Regressão e correlação
A regressão e correlação possui uma tentativa de manifestar uma equação matemática linear que descreva o relacionamento entre duas variáveis, uma sendo dependente e outra independente. Essa equação tem por finalidade estimar valores de uma variável, com fundamento em valores conhecidos da outra, por exemplo o peso e a idade.
A seguir mostraremos o modelo de regressão, em que a primeira parte antes da igualdade é o valor estimado, o alfa o coeficiente de regressão multiplicando pela variável independente, somando com o coeficiente linear e resíduo.
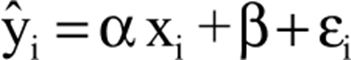
Destacando que na regressão, os valores de da incógnita y são estimados com base nos valores dados ou conhecidos pela incógnita x, sendo assim, a variável y é chamada de variável dependente e x variável independente.
1.9 Distribuição Binomial
Uma das distribuições mais utilizadas, ela baseia-se em eventos mutuamente exclusivos, chamados de sucesso e fracasso em que a ocorrência de um evento impossibilita a ocorrência do outro e independentes, isso significa que a probabilidade de um evento ocorrer não interfere na probabilidade do outro ocorrer também, assim podemos afirmar que essa distribuição parte do princípio de que todos os eventos sendo estes do mesmo experimento tenham as mesmas possibilidades de ocorrer. Para o seu cálculo é necessário ter três valores, número de sucessos (x), número de tentativas (n) e a probabilidade de sucesso em cada uma das tentativas registradas (p).
1.10 Método de Bernoulli
A distribuição binomial tem fundamentação nos termos do desenvolvimento do binômio de Newton, usado por Bernoulli, ou seja, seu cálculo é feito com análise combinatória entre as possibilidades de se obter sucessos ou fracassos para calcular a ocorrência dos experimentos, dito isso temos a seguinte fórmula:
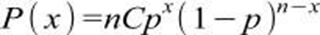
1.11 Distribuição de Poisson
A distribuição de Poisson é utilizada quando a variável aleatória está referida a uma adversidade, seja de tempo, superfície ou volume que possa assumir qualquer valor inteiro ou positivo, então pode-se dizer que essa distribuição consegue medir aqueles eventos que são dinâmicos não estáticos, com base em seu valor médio, ignorando a amostra exata, além disso, o experimento consiste na contagem de número de vezes (x) que o evento acontece em um determinado intervalo, esse intervalo pode ser expresso em tempo, área ou volume. Veremos sua fórmula a seguir, em que e é o número irracional, uma constante, com valor aproximado de 2,71828.
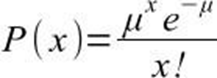
2 RESULTADOS
2.1 Número de Nascimentos resultando em cálculos iniciais
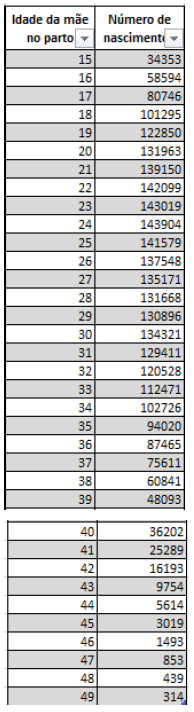
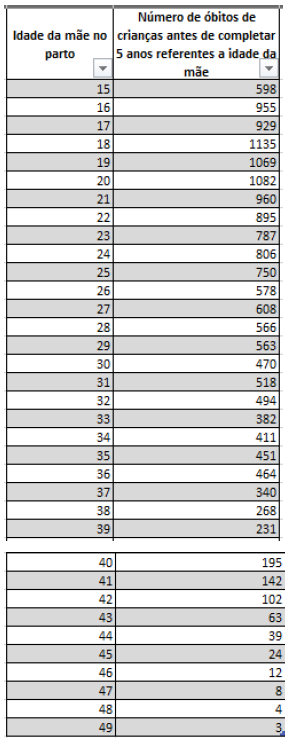
Quadro 1 – Amostra de dados
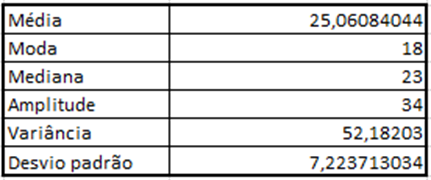
Quadro 2 – Resultados após cálculos
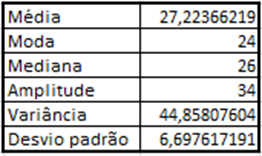
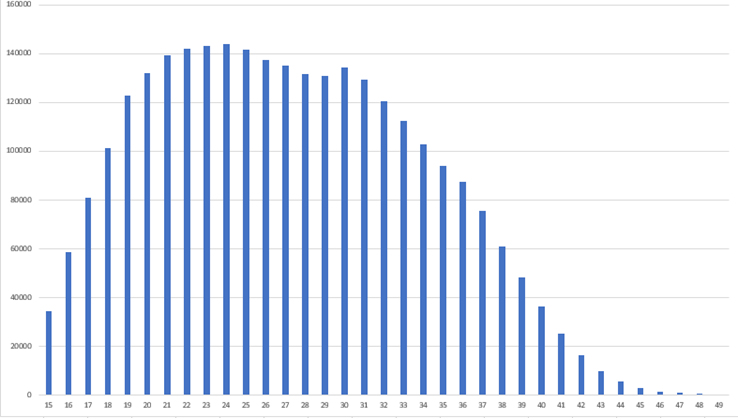
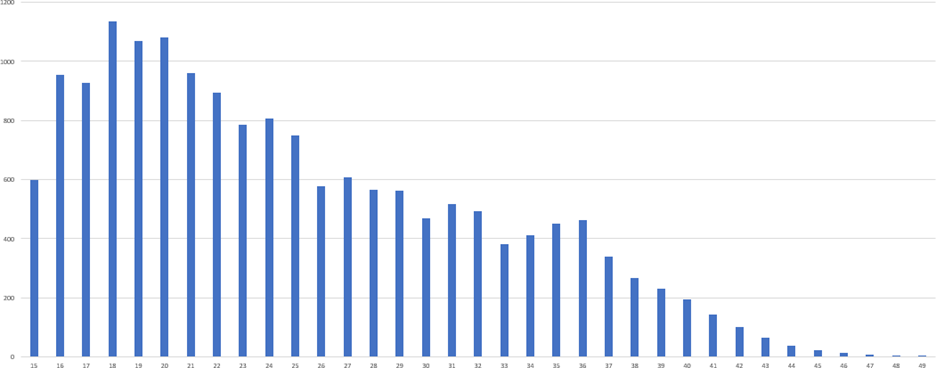
Gráfico 1 – Histograma referente ao número de nascimentos
2.2 Mortalidade Infantil resultando em cálculos iniciais
Gráfico 2 – Histograma referente a mortalidade infantil
Quadro 3 – Resultados após cálculos
Quadro 4 – Amostra de dados
2.3 Intervalo de confiança
De acordo com o número de nascimentos temos o seguinte quadro
Quadro 5 – Intervalo de confiança

Na sequência podemos observar o quadro de acordo com a mortalidade infantil.
Quadro 6 – Intervalo de confiança

2.4 Testes de hipótese
Com base no número de nascimentos, temos os seguintes resultados.
Quadro 7 – Teste de hipótese pela média

Quadro 8 – Teste de hipótese pela variância

Agora veremos os resultados obtidos conforme a mortalidade infantil.
Quadro 9 – Teste de hipótese pela média

Quadro 10 – Teste de hipótese pela variância

2.5 Testes de adequação
Como ambas as variáveis estão dispostas em valores maiores que 3,84 não são distribuições normais. Chegamos ao valor de estarem maiores para 3,84 após fazermos respectivos cálculos no Excel.
Distribuição Bernoulli, Binomial, Poisson e Normal
2.6 Distribuição Bernoulli, Binomial, Poisson e Normal
Quadro 11 – Distribuições para número de nascimentos
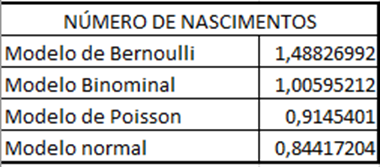
Gráfico 3 – Número de nascimentos
Quadro 12 – Distribuições para mortalidade infantil
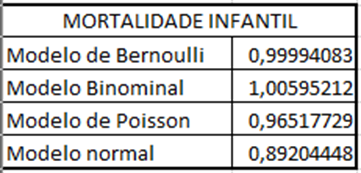
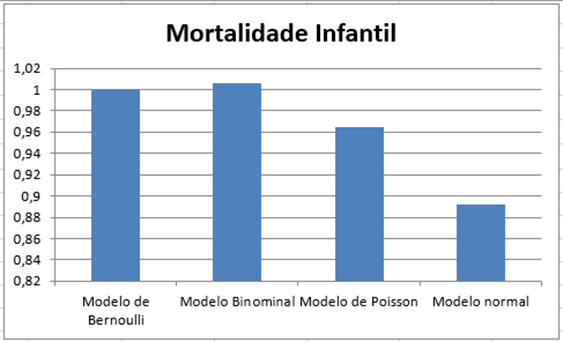
Gráfico 4 – Mortalidade infantil
2.7 Correlação e regressão
Quadro 13 – Correlação entre as duas amostras

Gráfico 5 – Número de nascimentos e óbitos
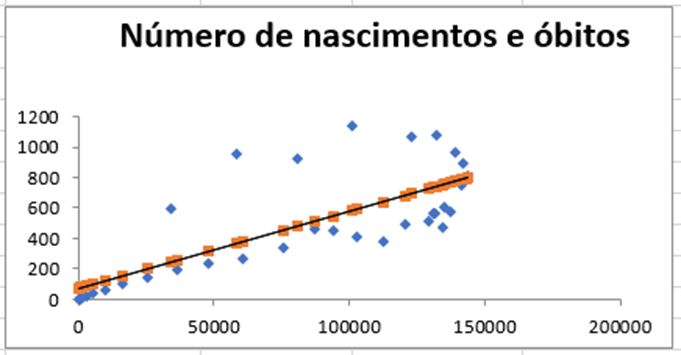
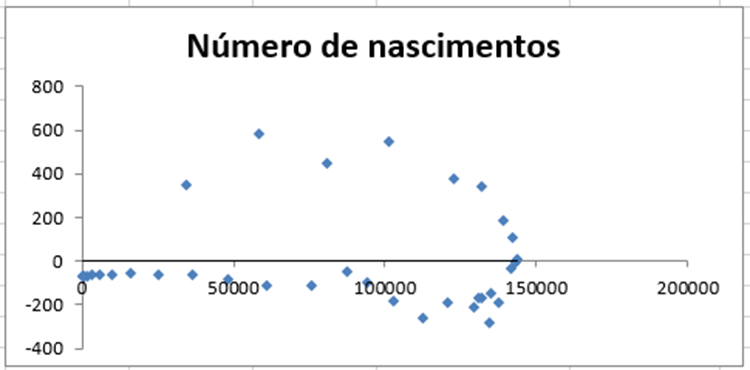
Gráfico 6 – Número de nascimentos
3 DISCUSSÃO
Após discussões feitas com todos os integrantes acerca de ambas as variáveis chegamos a algumas conclusões e interpretações que precisam estar registradas para dar embasamento a pesquisa.
Conforme vimos, temos dois tipos de testes de hipóteses, pela variância e média. O primeiro faz nós termos a concepção de que a variância será maior na mortalidade infantil pois ela atinge diretamente fatores biológicos e fatores acidentais, dessa forma, podemos exemplificar com situações que envolvem baixo peso ao nascer, prematuridade e presença de malformação congênita para fatores biológicos e para fatores acidentais temos envolvido nesse aspecto a falta de cuidado provocando quedas acidentais ou até mesmo acidentes domésticos. Além disso, podemos citar que condições de assistência que muitas vezes são negligenciadas, entre elas temos consultas de pré-natal.
Destacamos a seguir que o número de nascimentos pela média depende da idade da mãe, ou seja, de acordo com os cálculos obtidos percebemos que a aprovação está relacionada com a média de nascimentos maior que 26 anos.
As hipóteses a respeito do parâmetro populacional indicam que a taxa de mortalidade infantil são parcialmente independentemente do número de nascimentos, ou seja, quanto mais nova a mãe for, mais chances a criança têm de vir a óbito. Consequentemente mães que sofrem com as expressões de desigualdades sociais, incluindo a pobreza, sua raça e o estado civil, sofrem mais do que outras mães que possuem privilégios que ainda são tratados como tabu pela sociedade. Muitos profissionais ignoram o fato de que uma adolescente possa ter relações sexuais com 11 anos por exemplo e impedem que a mesma faça uso de métodos contraceptivos, como o anticoncepcional.
4 CONSIDERAÇÕES FINAIS
No mundo orientado a dados de hoje, a aplicação de estatísticas na vida cotidiana é uma realidade sempre presente que afeta todos os aspectos da sociedade. Embora o campo da estatística tenha se originado há séculos, o impacto explodiu nos últimos anos, à medida que os estatísticos modernos avançaram nas aplicações estatísticas por meio de abordagens inovadoras de solução de problemas.
Concluímos com a pesquisa em torno das duas variáveis que uma está totalmente relacionada a outra e os fatores envolvidos entre ambas afetam tanto a mãe quanto a criança. Acreditamos que a informação é a única maneira de conseguirmos modificar as estatísticas que crescem ano após ano, não devíamos nos conformar com a situação de que a morte infantil muitas vezes está ligada a uma adolescente que sofre com o óbito do filho e a violação aos direitos do adolescente, cobrando programas específicos para atender essa porcentagem de jovens e conscientizando responsáveis legais e profissionais.
5 REFERÊNCIAS
LARSON, Ron; FARBER, Betsy. Estatística aplicada. 6. ed. São Paulo: Pearson, 2016. CRESPO, Antônio Arnot. Estatística fácil. 19. ed. São Paulo: Saraiva, 2009
FEIJOO, A.M.L.C. Parte I – Estatística descritiva – 4. Medidas de tendência central. Rio de Janeiro : Centro Edelstein de Pesquisas Sociais, 2010.
GEBERT, D. Probabilidade e estatística I. Paraná Universidade Estadual de Ponta Grossa.
SINDELAR, F.C.W. CONTO, S.M. AHLERT, L. Teoria e prática em estatística paracursos de graduação. Leajeado: Editora Univates, 2014.
LOPES, L.F.D. Apostila estatística. Universidade Federal de Santa Maria, 2003. FREIRE, S.M. Bio
1https://orcid.org/0000-0001-7606-6696
email: irilanyvesgar@yahoo.fr
2email: paul.ingciv@hotmail.com

