REGISTRO DOI: 10.5281/zenodo.7762854
Carina Araújo Vieira1
Ririvaldo Pereira de Sousa2
Angela Maria Percinoto Trentini3
Priscila Dayene Rezende4
RESUMO
Em cálculos matemáticos, programas de computadores podem apresentar erros diversos quando é executado. Dois tipos de erros de grande importância são os erros de arredondamento e os erros de truncamento. Quando utilizamos funções matemáticas em aplicações desenvolvidas para as máquinas digitais (calculadoras, computadores, tablets, celulares, entre outros), devemos utilizar bibliotecas específicas que são disponibilizadas pela linguagem de programação utilizada pelo programador da aplicação. Muitas das funções matemáticas disponibilizadas nessas bibliotecas são desenvolvidas a partir de séries de Taylor ou séries de Maclaurin que são séries infinitas. Exemplos: funções trigonométricas, funções exponenciais, funções logarítmicas, entre outras, a função logarítmica para exemplificar esses erros desenvolveu a função lnx em série de Taylor (em torno de 1) e dê exemplo de como o valor da função pode ser modificado ao considerar diferentes números de termos.
PALAVRAS-CHAVE: Uso de aplicações digitais; tecnologia; logaritmo.
INTRODUÇÃO
É importante o estudo da matemática em todos os âmbitos da sociedade está inserido desde em pequenas resoluções como para a vida profissional, facilitando e melhorando a vida no dia a dia de cada um. São contas a pagar, a hora para concluir uma atividade, uma medição de área ou volume, parcelas de empréstimos consignados, dentre tantas atividades rotineiras que envolvem o uso da matemática.
As tecnologias digitais são muito utilizadas para facilitar estes cálculos, porém podem ocorrer erros de cálculos quando há juros que aumentam de tempo e tempo sem que ninguém tenha atualizado o programa prejudicando a todas as pessoas chamadas de “consumidores”, por isto que os gerentes de programação devem corrigir tais erros que podem ser devido aos cálculos em um determinado projeto arquitetônico do logaritmo no aplicativo de software.
Neste sentido saber os fundamentos da matemática vai além de conhecer os fundamentos matemáticos para corrigir os erros que poderemos encontrar e tomar as devidas soluções do problema. Com este intuito de analisar os erros de um aplicativo na empresa onde o software é que se torna fundamental o desenvolvimento do presente trabalho.
Por meio do mesmo será apresentada a correção devida dos cálculos de um empréstimo consignado, também será possível conhecer e interpretar os cálculos no contexto matemático. E ainda será apresentado contextos práticos com questões que tratam do uso da ferramenta digital na matemática cotidiana.
Assim se pretende com o objetivo da pesquisa a ser realizada é fundamentar o uso da matemática para conhecer os erros e os critérios que devem ser levantados para corrigir os cálculos realizados de duas arquiteturas que projetaram resultados diferentes.
Assim se pretende construir um relatório onde o gestor da empresa analise os cálculos matemáticos verificando os erros cometidos a fim de solucionar os erros cometidos e assim nos aprofundar para a vida pessoal e profissional.
DESENVOLVIMENTO
Diversas empresas estão utilizando as tecnologias digitais para resolver os problemas financeiros como parcelamentos seja na compra de produtos como de serviços por exemplo nos empréstimos consignados.
Hoje em dia as pessoas confiam na compra onde os cálculos matemáticos são realizados pelo aplicativo, porém, não percebem os erros que comentem quando há um aumento nestes cálculos, e muitas pessoas podem ser prejudicadas pelos juros abusivos diante destas falhas dos softwares e a empresa receber reclamações.
Conhecendo os cálculos utilizados no financiamento podem ser com juros simples ou juros compostos, onde os juros simples são cobrados em cima do capital inicial, enquanto os juros compostos se calculam pelo montante de cada período.
Tarefa 1: Modelo matemático para o cálculo das parcelas do empréstimo
Ao tomar emprestado um valor de R$ 1.000 a um amigo e terá que pagar juros simples de 8% ao mês. Para calcular quanto de juros você terá que pagar em cada parcela, basta fazer a seguinte conta:
1000 x 0,08 = 80
*0,08 = 8%
Com este cálculo você fica sabendo que a cada mês terá que devolver uma parte dos R$ 1.000 acrescida de R$ 80 de juros.
Para saber o valor total dos juros que você terá que pagar até a quitação da dívida, basta pegar o valor dos juros mensais (R$ 80) e multiplicar pelo número de parcelas definido para pagamento do empréstimo.
Vamos supor que você vai pagar em 5 vezes. O cálculo será:
80 x 5 = 400
Ou seja, você vai pagar R$ 400 só de juros para quitar o empréstimo.
a) Juros compostos
Nos juros compostos diferencia no aumento do valor anterior a cada período, por exemplo a tomar emprestado do banco o valor de R$ 1.000, que cobra juros compostos, e que vai fazer um pagamento único, referente ao principal mais os juros, numa data futura.
Nesse caso, o cálculo da taxa de juros será feito em cima do capital inicial (o valor do empréstimo) acrescido do valor dos juros cobrados no mês anterior, com exceção, obviamente, da primeira parcela, quando a taxa de juros é aplicada somente sobre o capital inicial. Vejamos então:
Primeiro mês:
1.000 x 0,08 = 80 –> R$ 80 é o valor dos juros que você vai pagar no primeiro mês.
Segundo mês:
1.000 + 80 (juros do primeiro mês) = 1.080 –> é sobre este valor (R$ 1.080) que você vai aplicar a taxa de juros para saber quanto pagará no segundo mês. Acompanhe a conta:
1.080 x 0,08 = 86,40–> R$ 86,40 é o valor dos juros que você vai pagar no segundo mês
Terceiro mês:
1.000 + 80 (juros do primeiro mês) + 86,40 (juros do segundo mês) = 1.166,40 –> é sobre esse valor que será aplicada a taxa de juros para definir o valor a ser pago no terceiro mês.
Veja:
1.166,40 x 0,08 = 93,312 –> R$ 93,312
R$ 93,312 é o valor dos juros que você vai pagar no terceiro mês.
Para saber quanto você vai pagar no total, somando o valor inicial com os juros compostos, basta usar a seguinte fórmula:

Tarefa 2: Erros em aplicativos para as máquinas digitais
Ao se direcionar a um aplicativo de software as pessoas acreditam nos cálculos realizados por eles, sendo os programadores as referências dos resultados obtidos, sendo necessário utilizar a função logarítmica na base e (lnx) para evitar erros nos resultados matemáticos nos softwares.
O erro da empresa Crefija era de não utilizar a função logarítmica na base e (lnx) na arquitetura de 64 bits, tendo que ser corrigido o mais rápido possível.
Assim, vamos conhecer os logaritmos do tipo log10 x . Esse logaritmo é definido como:

Onde o número 10 é denominado base do logaritmo. A figura abaixo mostra o gráfico da função logarítmica

Gráfico 1 :
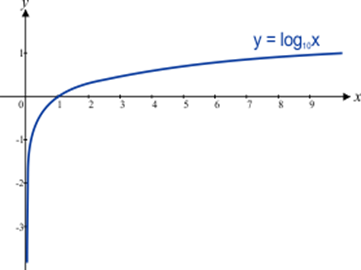
No estudo do Cálculo, a base mais utilizada para logaritmos é o número e. Nesse caso, o logaritmo
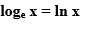
é denominado “logaritmo natural de x” e definido como

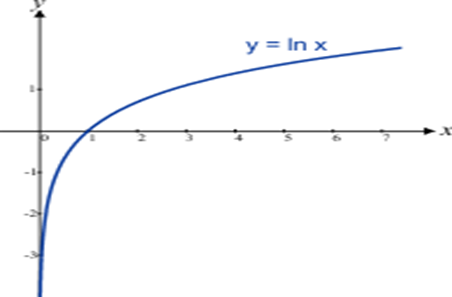
A figura abaixo mostra o gráfico da função logarítmica natural f(x) = In x
Gráfico 2 :
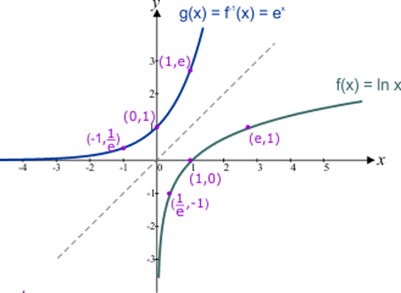
O domínio da função logarítmica natural y = f (x) = ln x é o conjunto dos números reais positivos, ou seja, o valor de y só pode ser calculado para valores de x > 0.
Como as funções f (x) = ln x e g (x) = ex são inversas uma da outra, então o domínio de f (x) = ln x é igual a imagem de g (x) = ex e a imagem de
f (x) = ln x é igual ao domínio de g(x) = ex.

Fonte: https://www.educamaisbrasil.com.br/enem/matematica/funcao-logaritmica
Gráfico 4 :
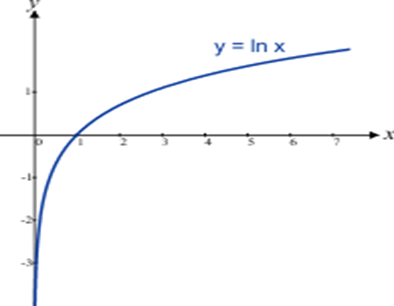
Observe que:
Se x > 0, então ln x é o expoente ao qual deve se elevar a base e para se obter o valor de x.
A definição de função logarítmica mostra que a função logarítmica natural
f(x) = ln x e a função exponencial natural g (x) = ex são funções inversas uma da outra. Isso significa que seus gráficos são reflexões um do outro em relação à reta y = x.
Gráfico 5 :
Observe que:
Se x > 0, então ln x é o expoente ao qual deve se elevar a base e para se obter o valor de x.
A definição de função logarítmica mostra que a função logarítmica natural
f(x) = ln x e a função exponencial natural g(x) = ex são funções inversas uma da outra. Isso significa que seus gráficos são reflexões um do outro em relação à reta y = x.
Tarefa 3: Arquitetura de 32 ou de 64 bits
Conforme o conceito de CARDOSO e DUARTE que define processador como sendo:
O termo “computador de 32 ou de 64 bits” diz respeito à arquitetura do processador e do sistema operacional empregados em uma determinada máquina. Ou seja, a maioria dos processadores atuais são capazes de processar dados e instruções de 64 ou de 32 bits. E é muito comum que as plataformas possuam versões compatíveis com as duas arquiteturas. (CARDOSO e DUARTE, 2021)
Cardoso e Duarte ainda explica que a capacidade de armazenamento no ponto de vista técnico o processador de 64 bits tem a capacidade de trabalhar de forma duplicada no processamento de palavras, podendo realizar apenas uma só vez o clock, elevando a capacidade de trabalho no hardware.
Nos computadores do Windows podemos encontrar o número de bits, onde o processador não precisará fazer operações complexas durante o processamento mesmo com 32 bits.
3 CONSIDERAÇÕES FINAIS
As tecnologias digitais favoreceram a população para facilitar as negociações entre pessoas e bens, onde muitos recorrem e acreditam que os resultados de cálculos numéricos estejam corretos sem perceber que podem ocorrer erros nos resultados destes cálculos.
Programações em diversas partes do mundo por meio da utilização de softwares sofisticados utilizam destas tecnologias, sendo desde investimentos e pagamentos, e o usuário utilizam constantemente onde através de logaritmos dão o resultado imediatamente.
O uso dos softwares tem sido utilizado por todas as pessoas que possuem empresas onde os serviços pela internet podem solucionar com maior rapidez e efetuando a compra e venda de determinados produtos.
Os conteúdos ensinados em matemáticos colocam os alunos em contato direto com diversas situações onde na prática, promovendo o raciocínio lógico e o saber diante de problemas que envolvam cálculos, onde possam chegar a respostas e resultados que irão apresentar alternativas absolutas para as questões cotidianas em que vivem.
Diante deste uso didático da matemática foi interessante ter o contato com o desenvolvimento de juros e ver sua aplicabilidade em situações cotidianas, como calcular as parcelas do empréstimo consignado, e outros.
Entende-se desta forma que usar a matemática a favor da vida diária e fazer os cálculos de forma manual é um aprendizado enriquecedor para o futuro acadêmico e profissional de tantos alunos que estão em sala de aula buscando conhecimento.
REFERÊNCIAS
BITTENCOURT, Thiago. Entenda qual é a diferença entre computadores de 32 e 64 bits. Disponível em: <https://www.techtudo.com.br/artigos/noticia/2013/06/entenda-qual-e-diferenca-entre-computadores-de-32-e-64-bits.html>. Acesso em: 28 jul. 2021.
BIZELLI, Maria Helena S. S. Cálculo Digital: Gráficos – Função logarítmica. Disponível em: <http://calculo.iq.unesp.br/sitenovo/Calculo1/funcao-graficos-logaritmica.html>. Acesso em: 28 jul. 2021.
CARDOSO, Beatriz; DUARTE, Nathalia. O aplicativo parou de funcionar: usuários relatam erro no android. Disponível em: <https://www.techtudo.com.br/noticias/2021/03/o-aplicativo-parou-de-funcionar-usuarios-relatam-erro-no-android.ghtml>. Acesso em: 28 jul. 2021.
SANTOS, Thamires. Função Logarítmica. Brasil Escola, 2019. Disponível em: <https://www.educamaisbrasil.com.br/enem/matematica/funcao-logaritmica>. Acesso em: 28 jul. 2021.
VASCONCELOS, Ester. Bancos digitais, são confiáveis? Disponível em: <https://www.jornalcontabil.com.br/bancos-digitais-posso-confiar/>. Acesso em 30 jul. 2021.
¹Graduada em licenciatura plena em Matemática pela UNOPAR (Universidade Norte do Paraná). Professora interina da rede pública do estado de Mato Grosso, Mestranda em Ciências da Educação pela UNADES – Universidad Del Sol / Paraguay.
2 Graduado em Licenciatura Plena em Letras pela UFMT (Universidade Federal de Mato Grosso). com Especialização em Educação Interdisciplinar pelas Faculdades Integradas Matogrossenses de Ciência Sociais e Humanas (Instituto Cuiabano de Educação). Professor efetivo da rede pública do estado de Mato Grosso, Mestrando em Ciências da Educação pela UNADES – Universidad Del Sol / Paraguay.
3Graduada em licenciatura plena em pedagogia pela UNIFLOR (União das faculdades de Alta Floresta), com especialização psicopedagia. Professora efetiva da rede pública do estado de Mato Grosso.
4Graduada em licenciatura plena em Letras pela UNIFLOR (União das faculdades de Alta Floresta), com especialização Ensino de língua portuguesa e literatura brasileira. Professora efetiva da rede pública do estado de Mato Grosso.
