REGISTRO DOI: 10.5281/zenodo.7761678
Thales Rodrigues Barboza1
Matheus Alves Lima2
Bruno de Oliveira Schneider3
Diunay Zuliani Mantegazini4
Andreas Nascimento5
RESUMO
O eixo é um elemento de máquina bastante utilizando para transmitir movimento e está sujeito a esforços de flexão, e devido a rotação do eixo, sempre sofrerá em um determinado ponto, hora esforços de tração, hora esforços de compressão. Devido a esses esforços repetidos, pequenas trincas podem surgir fazendo com que o elemento falhe por fadiga, ocasionado uma parada emergencial do equipamento. O objetivo deste trabalho é verificar o coeficiente de segurança à fadiga de um determinado eixo utilizado em uma bobina de papel através de resultados previamente calculados e simulados e demonstrar como os resultados simulados e analíticos podem ser diferentes. Dois tipos de apoios foram testados, bem como 3 tipos de malhas em cada apoio. Pode-se concluir que os resultados obtidos analiticamente foram diferentes dos resultados simulados e na simulação foi percebido que o tamanho de malha interfere e muito na resposta final.
PALAVRAS–CHAVE: Eixo, fadiga, análise, simulação.
1 INTRODUÇÃO
O eixo é um membro rotativo, usualmente de seção transversal circular, usado para transmitir potência ou movimento. Ele provê o áxis de rotação, ou oscilação, de elementos tais como engrenagens, polias, volantes, manivelas, rodas dentadas e similares, e controla a geometria de seus movimentos (Shigley, 2016).
Os componentes são ainda fixados usualmente sobre o eixo por meio de chavetas, pinos ou ajustes com interferência, além dos costumeiros e necessários mancais de rolamentos ou deslizamento, sempre presentes em casos e eixos rotativos (árvores) (Almeida et al, 2017).
Os eixos podem ser divididos em dois tipos, sendo os eixos que trabalham fixos, como por exemplo o eixo dianteiro de um veículo com tração traseira, e os eixos árvore, que trabalham em movimento, por exemplo, eixos que fazem parte da caixa de câmbio de um veículo (Sarkis, 2019).
Como se sabe, devidos aos esforços exercidos no eixo podem fazer com que venha falhar por fadiga, o que é algo bastante indesejado.
Silva (2010) aborda que a fadiga, é um fenômeno complexo que é caracterizado pela redução gradual da capacidade de elementos estruturais de suportar cargas cíclicas. Sendo que os danos relacionados a fadiga é um processo que vai se acumulando, pois é o resultado da aplicação de um grande número de ciclos de tensões. Vale ressaltar que a amplitude dos ciclos de tensão aplicada não precisa ser nenhum tipo de esforço considerado alto, o mesmo é baixa em relação à tensão de escoamento do metal, mas o grande número de aplicações repetidas pode levar à fratura do material.
A falha por fadiga inicia-se com uma pequena trinca superficial e ela vai progredindo durante o funcionamento da peça, devido ao efeito da concentração de tensões que aumenta com a propagação da trinca e, como consequência, a área sob tensão diminui de tamanho. A partir dessa condição as tensões aumentam exageradamente até que a peça falhe abruptamente. Associado a essa condição, a falha por fadiga não apresenta deformação perceptível antes da sua ruptura, o que torna esse fenômeno muito perigoso (Almeida et al, 2017).
Com isso, o trabalho busca utilizar a técnica de analisa por elementos finitos de um eixo que é utilizado em uma bobina de papel, com o objetivo de descobrir suas deformações, tensões e principalmente o coeficiente de segurança em fadiga, garantindo que o eixo não falhará.
A metodologia será dividida em duas partes, uma demonstrando os cálculos analíticos para obter o coeficiente de segurança de fadiga e a outra será utilizando o software ANSYS, a fim de comparar os resultados obtidos analiticamente. Serão realizadas 6 simulações com dois tipos de apoio, sendo que em cada apoio serão realizadas mais três simulações, que utilizarão tamanhos de malhas diferentes.
2 METODOLOGIA
O objeto de estudo deste artigo é um eixo, conforme dimensões apresentadas na Figura 1, utilizado como suporte por um rolo de papel de densidade 984 kg.m-3, com comprimento de 3,23 m, diâmetro externo da bobina de 1,50m e diâmetro interno de 0,22 m

Figura 1: Dimensões do eixo a ser analisado
Neste artigo são utilizadas duas metodologias para análise do problema a ser solucionado. A primeira é com base no livro Norton (2013), onde serão utilizados os conceitos para resolver o problema de forma analítica. A segunda parte é a utilização do software ANSYS onde serão aplicadas as condições de contorno na peça para verificar as reações, coeficientes de segurança, vida em fadiga etc.
2.1 Cálculos analítico
Para desenvolver o problema, optou-se pelo material aço SAE 4130, temperado e revenido a 800 ºF, com resistência de escoamento em tração (Sy) de 1193 MPa (173 kpsi) e resistência máxima em tração (Sut) de 1282 MPa (186 kpsi).
As equações abaixo foram aplicadas na mesma para obter o resultado desejado (coeficiente de segurança em fadiga).
2.1.1 Força peso
Para encontrar a força peso exercida por um material cilindro vazado a equação 1 pode ser aplicada.

Em que, W é a força peso, De é o diâmetro externo, Di é o diâmetro interno, L o comprimento da peça, p a densidade do material e g a força da gravidade.
2.1.2 Limite de resistência a fadiga para aços
O limite de resistência fadiga é o nível de tensão abaixo do qual não ocorrem mais falhas por fadiga, podendo-se continuar os ciclos de tensão ilimitadamente (NORTON, 2013) e pode ser expresso conforme a equação 2.

Em que Se’ é o limite de fadiga não corrigido.
2.1.3 Fatores de correção para a resistência à fadiga ou limite de fadiga teóricos
São utilizados para considerar os as diferenças físicas existentes entre os corpos de prova e a peça real que está sendo analisada. Pode ser representada como:

Em que Se representa o limite de fadiga corrigido para um material que exibe um ponto de inflexão em sua curva S-N.
2.1.3.1 Efeitos da solicitação
Como os dados publicados de resistência a fadiga se referem a ensaios sob flexão rotativa, um fator de redução da resistência para a solicitação devido à força normal e flexão deve ser aplicado conforme equações 4a e 4b.

2.1.3.2 Efeitos do tamanho
Este fator tem por finalidade reduzir a resistência, logo o fator deve ser aplicado em peças maiores, pois as mesmas falham sob tensões menores, devido à maior probabilidade de um defeito estar presente na área sob tensão.
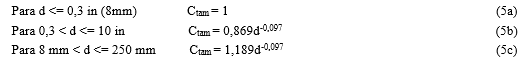
2.1.3.3 Efeitos de superfície
Acabamentos mais grosseiros diminuem a resistência à fadiga devido à introdução de concentrações de tensão e/ou alteração das propriedades físicas da camada superficial da peça. Uma superfície forjada é rugosa e descarbonizada e os reduzidos níveis de carbono enfraquecem a superfície, onde as tensões são frequentemente as mais elevadas. Logo, o fator de superfície da equação 6 é aplicado com auxílio dos dados da tabela 1, que depende do tipo de acabamento superficial da peça.

Tabela 1: Coeficientes para a equação do fator de superfície (Para Sut em MPa)

2.1.3.4 Efeitos de temperatura
Devido os ensaios de fadiga serem realizados a temperatura ambiente, é notório saber que a tenacidade à fratura diminui a baixas temperaturas e aumenta de valor em temperaturas moderadamente elevadas. Também a resistência ao escoamento diminui continuamente com temperaturas acima da temperatura ambiente, podendo provocar escoamento antes da falha por fadiga. Logo, para melhor aproximação, um coeficiente de temperatura deverá ser aplicado conforme às equações 7a, 7b e 7c.

2.1.3.5 Efeitos de confiabilidade
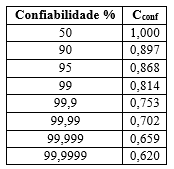
Muitos dos dados de resistência registrados na literatura referem-se a valores médios. Existe, no entanto, uma considerável dispersão nos ensaios realizados com o mesmo material sob condições semelhantes de ensaio. Devido a isso, na Tabela 2 é apresentado os fatores de confiabilidade para um valor assumido para o desvio-padrão igual a 8% da média.
Tabela 2: Fatores de confiabilidade para Sd = 0,08μ.
2.1.4 Efeitos da concentração de tensão
Para dimensionar o eixo de forma a considerar as concentrações de tensões existentes na peça, a Figura 2 será utilizada para prever o fator de concentração de tensão Kt.
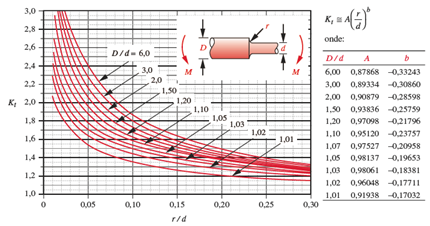
Figura 2. Fator geométrico de concentração de tensão Kt para um eixo com um rebaixo arredondado em flexão (NORTON, 2013).
2.1.5 Sensibilidade ao entalhe
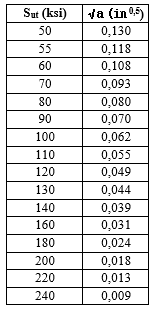
A sensibilidade ao entalhe está ligada ao raio de arredondamento do entelhe, medindo o quão bruscas são as descontinuidades da peça. Na Tabela 3 é apresentado a constante de Neuber para os aços que é de acordo com o limite de resistência a tração do material. Observe que a constante de Neuber é definida como a raiz quadrada de a, não como a, portanto é diretamente substituída na Equação 6, enquanto o valor de r deve ter sua raiz quadrada extraída.
Tabela 3: Constante de Neuber para aços

2.1.6 Fator de concentração de tensões em fadiga

Em que Kt é o fator de concentração de tensões teórico (estático) para a geometria particular e Kf é o fator de concentração de tensões em fadiga (dinâmico). A sensibilidade ao entalhe q varia entre 0 e 1. Essa equação pode ser reescrita para determinar Kf.
2.1.7 Tensão de flexão atuante
Para descobrir o valor de tensão real atuante na pesa, será utilizado a equação 10, aplicando o coeficiente de concentração de tensão e a tensão de flexão nominal que é descrita peça equação 11, em que M é o momento, C é o raio e I é o momento de inércia.

2.1.8 Coeficiente de segurança
Para chegar ao resultado desejado, será utilizado a equação 12 para verificar qual será o coeficiente de segurança do eixo.

2.2 Análise por simulação
Para obter resultados que possam servir de comparação com os resultados analíticos, a peça será desenhada no programa ANSYS dentro do ambiente DesignModeler e posteriormente passará por uma análise de elementos finitos com o intuito de verificar algumas respostas quanto a solicitação da carga aplicada ao eixo.
Para o modelo, serão realizadas seis simulações que se alternarão em dois tipos de suportes, o suporte fixo e o suporte cilíndrico. Dentro de cada tipo de suporte, serão utilizados três tipos de malhas diferentes, sendo as malhas de tamanhos default, 5 mm e 25 mm. Para análise do modelo, serão verificadas as soluções de deformação direcional, tensão equivalente de deformação, tensão equivalente, tensão normal, fator de segurança, vida em fadiga, fator de segurança em fadiga e sensibilidade em fadiga.
3 RESULTADOS
3.1 Resultado analítico
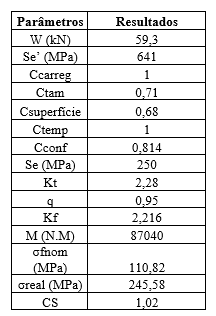
No primeiro momento para encontrar o coeficiente de segurança a fadiga foi calculado a força exercida pela bobina utilizando a equação 1, cujo valor foi de 59,3 kN. Está força irá atuar na extremidade do eixo como uma força pontual conforme figura 3.

Figura 3: Força aplicada no eixo
Para obter os resultados dos efeitos de solicitação, o eixo foi considerado como em flexão, logo seu resultado é igual a 1. Para efeitos do tamanho, foi utilizado a equação 5c, pois o diâmetro do eixo está compreendido na mesma faixa (d = 200 mm). Para efeitos de superfície foi considerado que o eixo apresentaria um acabamento superficial usinado, devido ao seu processo de fabricação. Para efeitos de temperatura a equação 7a é satisfatória, pois o eixo em exercício não passará da temperatura de 450 ºC (1). Para os efeitos de confiabilidade, foi considerado para os cálculos uma confiabilidade de 99% (0,814).
Analisando os efeitos da concentração de tesão na peça provocado pela mudança de diâmetro (200 para 220 mm), a Figura 2 foi utilizada para obter esses efeitos, sabendo que a relação D/d é igual a 1,1, logo os parâmetros A e B foram utilizados e chegou-se ao resultado de 2,28. A sensibilidade ao entalhe foi calculada com auxílio da equação 8, porém, foi necessário utilizar a constante de Neuber para os aços através do valor do Sut em ksi. O valor obtido aproximado para um Sut de 186 ksi foi de 0,0219, e esse valor foi substituído na equação 8.
Os demais parâmetros foram calculados conforme a metodologia apresentada, e os resultados podem ser vistos na tabela 4.
Tabela 4: Resultados analíticos
3.2 Resultados obtido por simulação
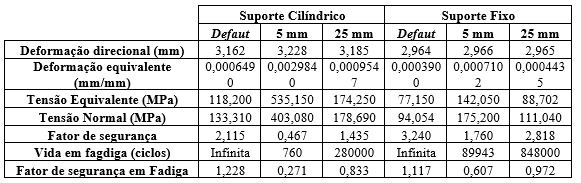
Após realizadas as devidas simulações, os resultados para cada uma delas podem ser verificados na tabela 5 e as imagens correspondentes podem facilmente serem visualizadas no anexo.
Tabela 5: Resultados das simulações
4 CONCLUSÃO
Diante dos resultados obtidos, pode-se se concluir que a resolução analítica do problema obtém resultados coerentes, que devem ser levados em consideração na hora que o eixo for projetado.
Dos resultados simulados, verificou-se que muitos deles foram bem próximos, porém, apresentando algumas divergências quando a malha era alterada. Isso pode ser um ponto desfavorável, pois pode levar a tomada de decisões precipitadas na hora de projetar e definir caracteristicas do eixo apresentado.
Apenas uma simulação apresentou vida infina para fadiga, corroborando com o resultado analítico, porém, não foi levado em consideração a alteração do diâmetro, logo a concentração de tensão. A malha default que apresentou esse resultado foi considerando o suporte fixo, e também foi possível demonstrar que a escolha da malha pode afetar e muito a simulação e portanto o resultado final.
Portanto, na hora de simular eixos ou qualquer tipo de elemento em qualquer programa computacional, é muito importante que quem o faça seja alguém com conhecimento prévio em engenharia e que possa levar para dentro da simulação considerações pertinentes, para assim, evitar que os resultados sejam muito dispersos da realidade, o que pode comprometer o equipamento, bem como colocar em risco a vida do operador.
REFERÊNCIAS
Almeida, J. C. Elementos de Máquinas – Projeto de Sistemas Mecânicos. Rio de Janeiro: Grupo GEN, 2017. 9788595152991. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788595152991/. Acesso em: 01 Dec 2022.
Bandeira, Carlos Filipe Cardoso. Análise de fadiga multiaxial em elementos estruturais tubulares sujeitos à vibração forçada. 2014. 97 f. TCC (Graduação) – Curso de Engenharia Mecânica, Centro Federal de Educação Tecnológica Celso Suckow da Fonseca, Rio de Janeiro, 2014.
Keith, B.R.N. J. Elementos de Máquinas de Shigley. Porto Alegre: Grupo A, 2016. 9788580555554. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788580555554/. Acesso em: 01 Dec 2022.
Norton, R. L. Projeto de Máquinas. Porto Alegre: Grupo A, 2013. 9788582600238. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788582600238/. Acesso em: 01 Dec 2022.
Sarkis, M. Elementos de máquinas. São Paulo: Editora Saraiva, 2019. 9788536530420. Disponível em: https://integrada.minhabiblioteca.com.br/#/books/9788536530420/. Acesso em: 01 Dec 2022.
SILVA, Rafael Aguera Rezeno da. Modelagem e simulação do mecanismo biela manivela e análise estrutural de biela automotiva. 2013. 57 f. TCC (Doutorado) – Curso de Engenharia Mecânica, Universidade Estadual Paulista, Faculdade de Engenharia de Guaratinguetá,, Guaratinguetá, 2013.
ANEXO
Suporte: Cilíndrico;
Tamanho de malha: Default
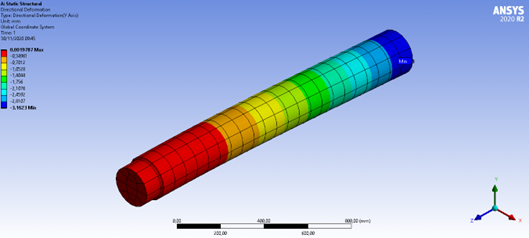
Figura 4: Deformação direcional (Y)
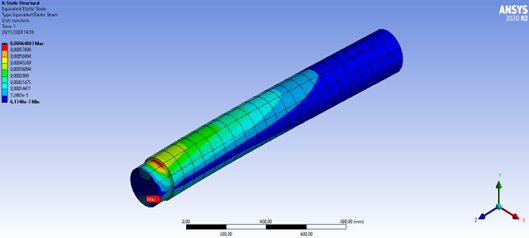
Figura 5: Deformação equivalente
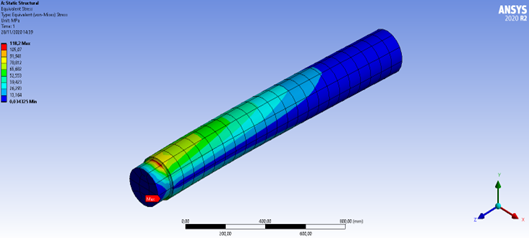
Figura 6: Tensão de von-Mises
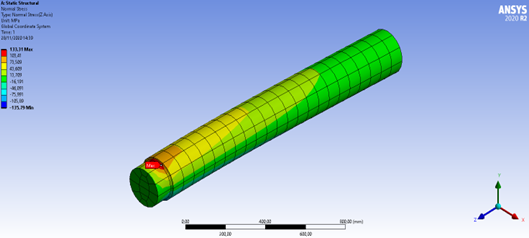
Figura 7: Tensão normal
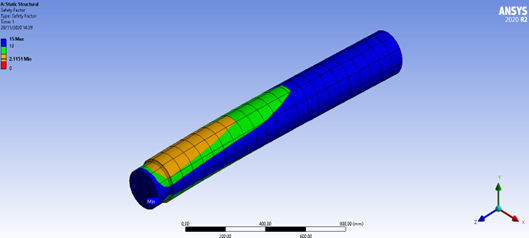
Figura 8: Fator de segurança.

Figura 9: Vida em fadiga

Figura 10: Fator de segurança em fadiga
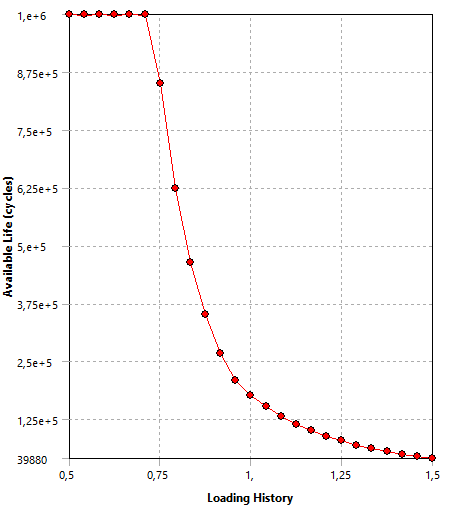
Figura 11: Sensibilidade à Fadiga
Suporte: Cilíndrico
Tamanho de malha: 5 mm
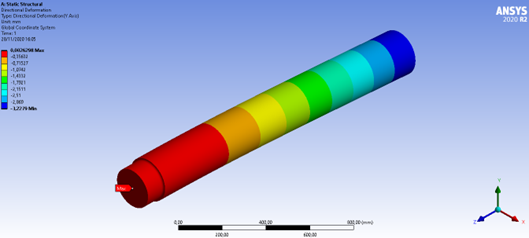
Figura 12: Deformação direcional (Y)

Figura 13: Deformação equivalente

Figura 14: Tensão de von-Mises

Figura 15: Tensão normal
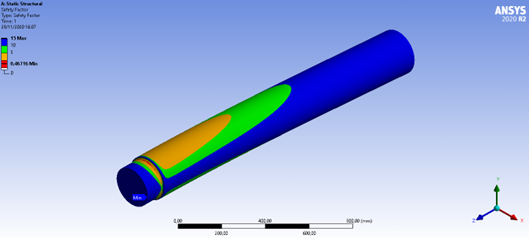
Figura 16: Fator de segurança
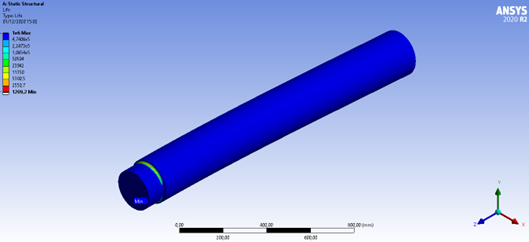
Figura 17: Vida em fadiga
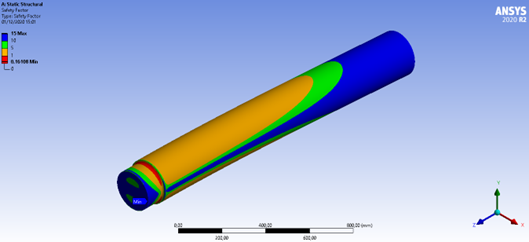
Figura 18: Fator de segurança em fadiga
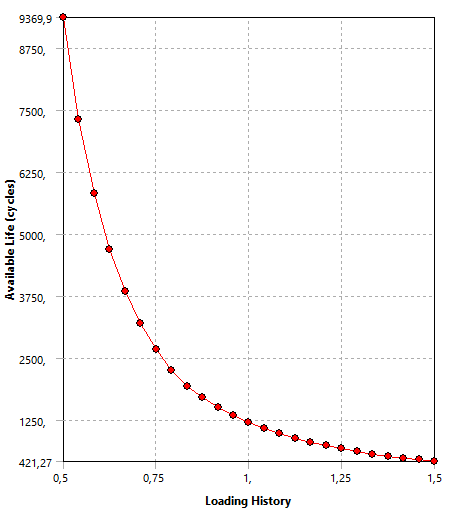
Figura 19: Sensibilidade à Fadiga
Suporte: Cilíndrico
Tamanho de malha: 25 mm
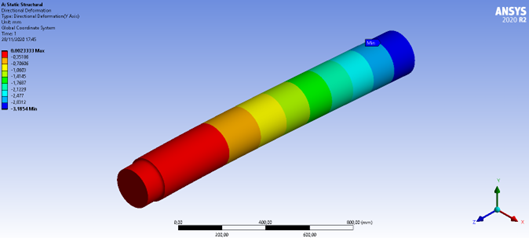
Figura 20: Deformação direcional (Y)
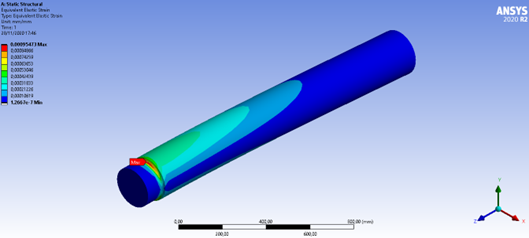
Figura 21: Deformação equivalente
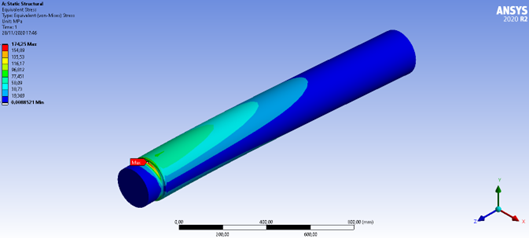
Figura 22: Tensão de von-Mises

Figura 23:Tensão normal
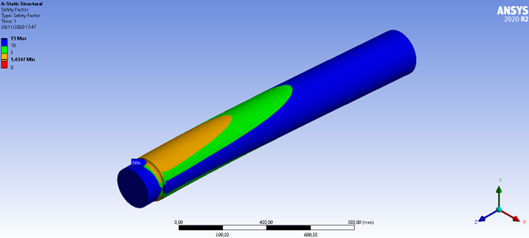
Figura 24: Fator de segurança
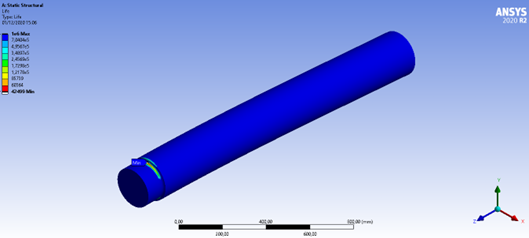
Figura 25: Vida em fadiga
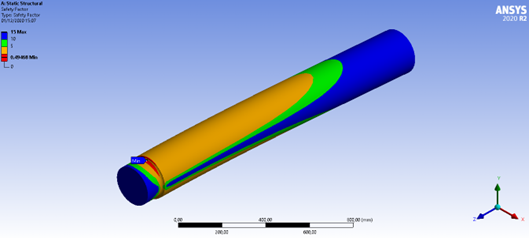
Figura 26: Fator de segurança em fadiga
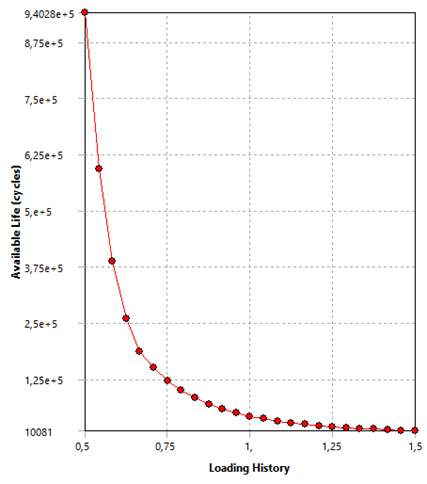
Figura 27: Sensibilidade à Fadiga
Suporte: Fixo
Tamanho de malha: Default
Figura 28: Deformação direcional (Y)
Figura 29: Deformação equivalente
Figura 30: Tensão de von-Mises

Figura 31: Tensão normal
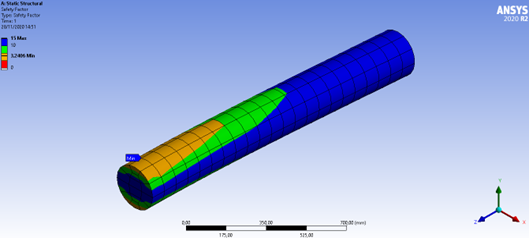
Figura 32: Fator de segurança

Figura 33: Vida em fadiga
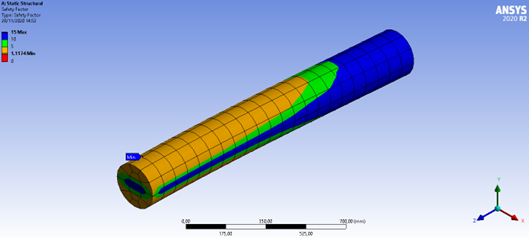
Figura 34: Fator de segurança em fadiga
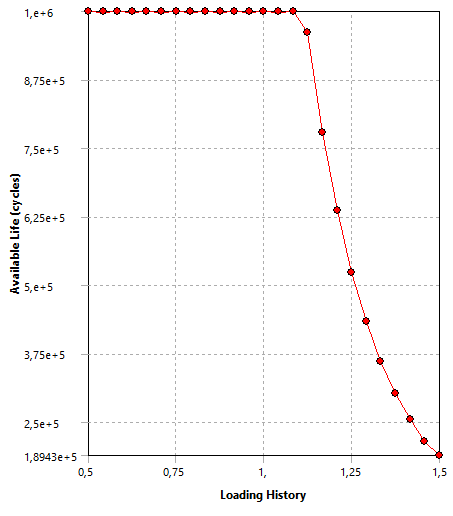
Figura 35: Sensibilidade à Fadiga
Suporte: Fixo
Tamanho de malha: 5 mm
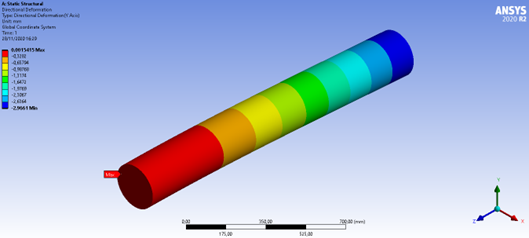
Figura 36: Deformação direcional (Y)
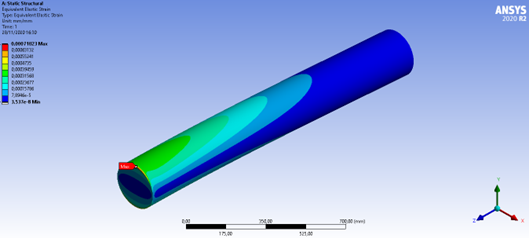
Figura 37: Deformação equivalente
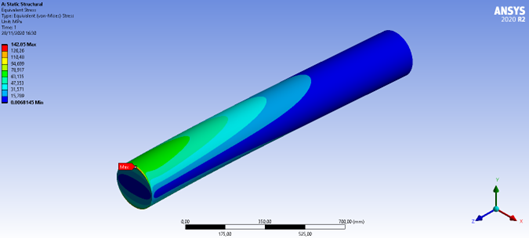
Figura 38:Tensão de von-Mises
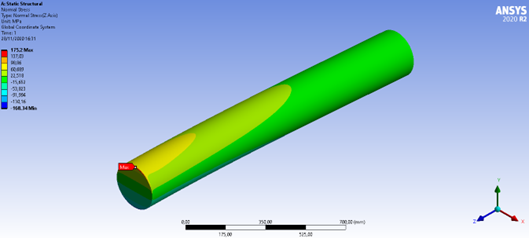
Figura 39: Tensão normal
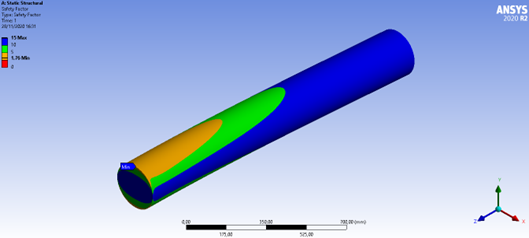
Figura 40: Fator de segurança

Figura 41: Vida em fadiga
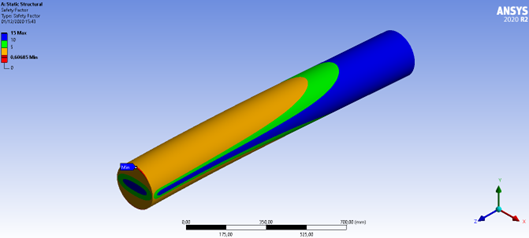
Figura 42: Fator de segurança em fadiga
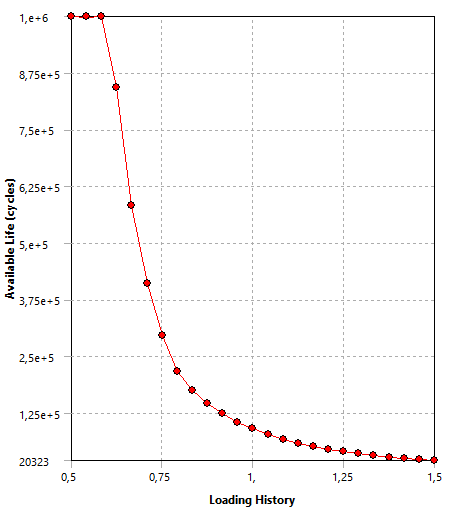
Figura 43: Sensibilidade à Fadiga
Suporte: Fixo
Tamanho de malha: 25 mm
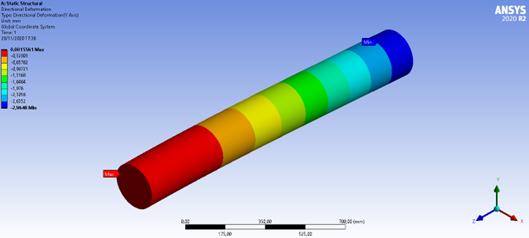
Figura 44: Deformação direcional (Y)
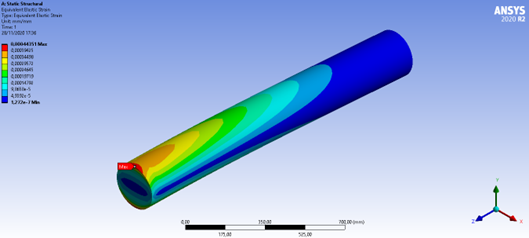
Figura 45: Deformação equivalente
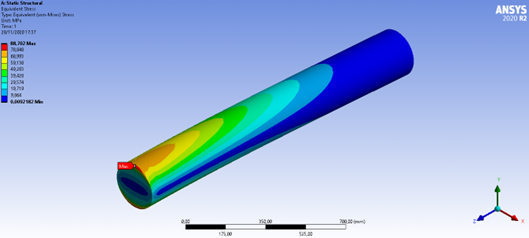
Figura 46: Tensão de von-Mises
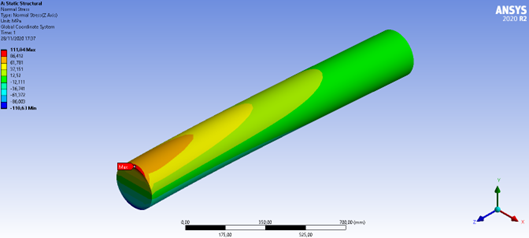
Figura 47: Tensão normal
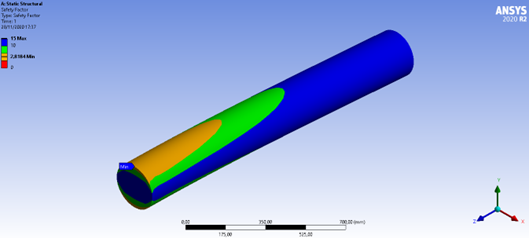
Figura 48: Fator de segurança

Figura 49: Vida em fadiga
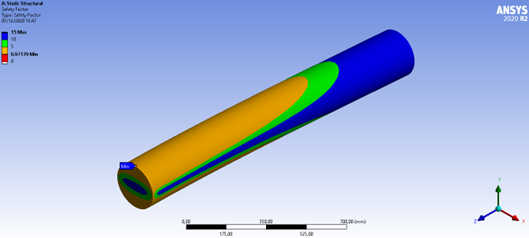
Figura 50: Fator de segurança em fadiga
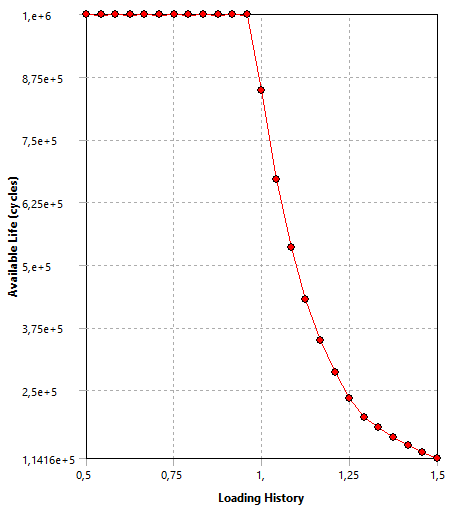
Figura 51: Sensibilidade à Fadiga
1Programa de Pós-graduação em Engenharia, Faculdade de Engenharia e Ciência de Guaratinguetá Universidade Estadual Paulista UNESP.
2Instituto Federal do Espírito Santo.
3Universidade Federal do Espírito Santo.
4Programa de Pós-graduação em Engenharia, Faculdade de Engenharia e Ciência de Guaratinguetá Universidade Estadual Paulista UNESP.
5Programa de Pós-graduação em Engenharia, Faculdade de Engenharia e Ciência de Guaratinguetá Universidade Estadual Paulista UNESP.Energy Group, Instituto de Engenharia Mecânica Universidade Federal de Itajub – UNIFEI.
