REGISTRO DOI: 10.5281/zenodo.7446989
Alessandro da Silva
INTRODUÇÃO
A Matemática trata com conceitos, procedimentos, teoremas, definições e demonstrações, isto é, ela é formada de constituintes abstratos. Por isso podemos dizer que a Matemática é abstrata. Consequentemente o ensino efetivo da Matemática deveria promover o processo de abstração. Na realidade, as práticas costumeiras de ensino tomam o primeiro lugar e muitos estudantes não conseguem relacionar as ideias matemáticas abstratas com o mundo prático e aqueles que conseguem ir bem nos exames escolares, normalmente não conseguem exemplificar os conceitos que aprenderam ou até mesmo citar exemplos de situações em que poderiam ser aplicados.
Por exemplo, existe um método tradicional aplicado nas escolas que se chama método ABC (Abstract Before Concret). Nele os conceitos e procedimentos abstratos são ensinados antes dos exemplos concretos e práticos. A teoria é que “o conhecimento adquirido em circunstâncias sem contexto deve estar disponível para aplicação com generalidade, isto é, em todos os contextos” (Lave, 1988, p.9), mas na prática, essa teoria não acontece. O conhecimento livre de contexto é chamado de abstract-apart (Mitchelmore & White, 1995) e não pode ser facilmente relacionado às situações familiares. Os conceitos só podem ser facilmente aplicados se forem abstract-general, ou seja, se eles representam o que é comum para uma variedade de situações. O método ABC prossegue em sentido oposto ao processo de abstração. Um outro exemplo é o ensino da matemática através do construtivismo. Muitos construtivistas enfatizam a necessidade de as crianças construírem sua própria compreensão, mas diferentemente de Piaget, raramente falam em abstração. As exceções devem ser encontradas nas obras de Dubinsky (por exemplo, 1991) e von Glasersfeld (por exemplo, 1995). O construtivismo enfatiza a discussão de conhecimento e das experiências que o aluno já possui, promove o desafio e a diversidade de soluções na resolução de problemas e permite o uso do aprendizado cooperativo de pequenos grupos. A questão é que no construtivismo não há preocupação em seguir um planejamento pré-determinado de conteúdos da matemática e isso inviabiliza sua aplicação no dia a dia escolar. Além disso, na opinião de Mitchelmore e White, ao invés de simplesmente esperar que as ideias matemáticas abstratas se desenvolvam como resultado da aprendizagem cooperativa da reflexão sobre a experiência, uma tentativa mais deliberada de promover a abstração de conceitos matemáticos cruciais contribuiria de forma considerável para a aprendizagem do aluno. Diante dessa realidade, Mitchelmore e White sugerem o ensino por abstração.
EMBASAMENTO TEÓRICO
A teoria em estudo se baseia nos trabalhos de Dienes, Piaget e Skemp onde os conceitos são formados quando as experiências estão conectadas entre si no sentido das suas similaridades. As ideias principais implícitas na abordagem da formação dos conceitos são: classificação, semelhança, abstração e conceito. Mitchelmore e White (2000) utilizam o entendimento de Skemp sobre a abstração para desenvolver uma abordagem de abstração empírica na aprendizagem matemática elementar, com foco em semelhanças de estruturas subjacentes a objetos ou situações. Skemp resume sua teoria da seguinte forma:
“Abstrair é uma atividade pela qual nós nos damos conta de semelhanças […] entre nossas experiências. Classificar significa coletar nossas experiências na base destas semelhanças. Uma abstração é algum tipo de mudança duradoura, o resultado da abstração é que nos permite reconhecer novas experiências como tendo as semelhanças de uma classe já formada. […] Para distinguir entre abstração como uma atividade e abstração como seu produto-final, nós […] chamaremos o último de conceito. (SKEMP, 1986, p. 21, apud MITCHELMORE; WHITE, 2000, p.211).”
Com relação à formação dos conceitos do dia a dia (como bolsa, faca e blusa) as semelhanças ficam no campo da aparência e propósito. Isto remete ao que Piaget chamou de abstração empírica dos conceitos diários. Para os conceitos matemáticos (como três) a classificação e abstração acontecem praticamente da mesma forma, mas com a diferença de que o objeto matemático a ser classificado não é concreto nem mental, mas envolve uma relação consistente entre eles. Por exemplo, o conceito abstrato “três” surge de uma contagem de um conjunto de objetos (um, dois, três) que sempre termina no mesmo número, independentemente da ordem dos objetos. Piaget chamou o processo de formação dos conceitos logico-matemáticos elementares de abstração reflexiva, e enfatizou que este é um processo essencialmente construtivo que não só constrói novos objetos mentais, mas que também constrói uma estrutura que os relaciona. “A abstração [matemática] é desenhada não do objeto que é agido sobre, mas da ação em si” (Piaget, 1970, p.16). Para Mitchelmore e White (2000), a abstração é o processo de reconhecimento e reificação (transformação em coisa) das similaridades entre um conjunto de objetos, eventos e ideias previamente não relacionados. Assim, a abstração forma um novo objeto mental que representa uma classe de objetos ou experiências.
O processo de abstração é progressivo e pode ser construído a partir de três princípios essenciais: familiarização, similarização e reificação. Na fase da familiarização desenvolve-se as regras operacionais em diversos contextos específicos, familiares e do cotidiano do aprendiz. Os estudantes se tornam familiarizados com muitos contextos nos quais o conceito será abstraído, antes mesmo do professor ensinar o conceito em si. Os exemplos serão discutidos usando uma linguagem peculiar ao contexto explorado e que seja natural para o aluno. Por exemplo, ao se ensinar ângulo, o professor poderá explorar os conceitos como canto, inclinação, rotação e abertura. O professor não falará em ângulo, ainda, mas irá direcionar toda a atividade para a abstração deste conceito incluindo declives e voltas em que os dois lados do ângulo abstrato são claramente visíveis.
Na fase da similarização demonstra-se que a mesma estrutura está presente em outros contextos. O conceito é ensinado dando oportunidade ao aluno de encontrar e tornar evidentes as semelhanças entre os exemplos familiares desse tal conceito. As semelhanças podem ser superficiais, como por exemplo, entre cantos e tesouras ou podem ser estruturais como as formas diferentes de se representar uma mesma fração em situações diferentes, como por exemplo 1/4 e 25%. Independentemente, a atenção dos alunos é direcionada aos atributos críticos que definem essas semelhanças e que são incorporados no conceito a ser abstraído. O professor então apresenta a linguagem específica associada ao conceito e usa esse vocabulário para definir matematicamente o conceito, mostrando como se relaciona com as semelhanças em que se baseia.
Por último, na reificação, os estudantes exploram os conceitos com mais detalhes com o uso de fórmulas e símbolos, por exemplo. A estrutura se torna progressivamente um objeto mental, destacado de qualquer contexto específico. Atividades diversificadas sobre um conceito, sempre mantendo uma relação entre os aspectos familiares e abstratos do mesmo, pode auxiliar a sua reificação. Alguns exemplos:
- Pedir para que o aluno encontre uma aplicação prática do conceito. Se for sobre áreas, pode-se estimar a área de uma escola representada em um mapa.
- Investigar como operacionalizar os representantes do conceito abstrato, sempre relacionando o resultado com algum contexto familiar. Se for sobre frações pode-se pedir para calcular 2/3 de 3/4 e depois checar a operação por meio de diagramas.
- Definir e trabalhar casos especiais do conceito como entender que porcentagens são frações especiais.
- Procurar por generalizações envolvendo o conceito, por exemplo, as fórmulas de áreas.
Segundo Mitchelmore e White (2000), os termos “generalização” e “abstração” são frequentemente confundidos na literatura. Entretanto, a diferença essencial entre eles é que a abstração cria um novo objeto mental, um conceito, enquanto na generalização estende o significado de um conceito existente a outras situações.
EXEMPLO DE APLICAÇÃO DA TEORIA
De acordo com Mitchelmore e White (2000), estudos mostram que crianças conseguem formar facilmente os conceitos de canto, inclinação e volta, mas têm dificuldade em integrá-los em um único conceito, que é o de ângulo. Além disso mostra que, enquanto a maioria das crianças veem os cantos em móveis, paredes e interseções das ruas como semelhantes em sentido angular, as tesouras e postes inclinados não são facilmente reconhecidos como tendo cantos. Um outro dado obtido de estudo é que cerca de um terço dos alunos de 8 anos que foram observados não podiam demonstrar a similaridade entre os ângulos que se mostram nos cantos e os ângulos que se mostram na roda giratória e na abertura de porta.
Os conceitos de canto, inclinação, abertura e volta são baseados em semelhanças superficiais: os cantos têm dois lados do ângulo visíveis (mais ou menos), a inclinação parece ser uma linha reta estática que gira em torno de um ponto e rodar é um movimento global que não precisa envolver quaisquer linhas ou pontos óbvios. Para formar um conceito de ângulo, as crianças precisam reconhecer uma semelhança mais profunda entre todos esses exemplos, ou seja, em que todos elas possam ser representadas por ângulos. Para ensinar o conceito de ângulo por abstração o professor deve, num primeiro momento, ajudar os alunos a abstraírem cada tipo de conceito como cantos, inclinações, giros e aberturas, observando em diversos exemplos as similaridades superficiais. O quadro abaixo exibe exemplos de objetos selecionados por Mitchelmore e White que estão no cotidiano das crianças. A roda, a porta, a tesoura e o leque estão inseridos no conceito de ângulo dinâmico e os demais no conceito de ângulo estático. A roda dá a ideia de giro ilimitado e os lados do angulo não são visíveis. No caso da porta, tesoura e leque pode-se enfatizar a abertura e fechamento dos braços, por serem facilmente reconhecidos e semelhantes aos ângulos de medidas diferentes. O poste, colina, junção, azulejo e parede podem representar ângulos de medida fixa. Por exemplo, o angulo de reto poderia ser representado pela parede.
Quadro 1: Modelos de situações de ângulos
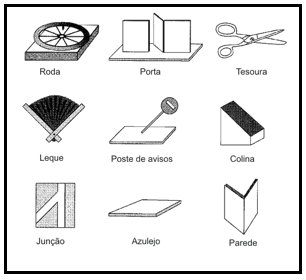
Fonte: Mitchelmore & White (2000, p. 221)
Após esse reconhecimento inicial, o professor levaria as crianças a vincular os conceitos de cantos, voltas e aberturas procurando semelhanças tanto na configuração geométrica quanto na medição de cantos, inclinações e voltas (figuras 1, 2, 3 e 4). Por exemplo, o ângulo reto desempenha um papel significativo em diversos casos e quatro ângulos retos completariam um ângulo de uma volta. A partir das semelhanças pode ser feito um desenho genérico (de um ângulo), que seria nomeado de “ângulo”. Como o conceito de ângulo teria sido abstraído de três contextos superficialmente diferentes, seria um conceito abstract-general.
O próximo estágio será generalizar o conceito de ângulo, primeiro com inclinações e depois com outros contextos como direção e ricochetes (reflexo depois de um corpo se chocar ou tocar o chão). Esses contextos são mais complexos do que cantos, voltas, e aberturas. Esse últimos precisam ser estudados primeiro por conta de suas características próprias. Por exemplo, a inclinação é mais exigente, pois envolve o conceito físico de horizontal de modo que sua inclusão no conceito de ângulo deve aguardar até que a física correspondente seja compreendida.
Figura 1: Representações em contexto de declives
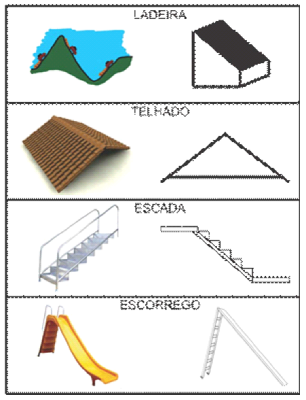
Fonte: Kléber Mendes Vieira (2010)
Figura 2: Representações em contexto de cantos
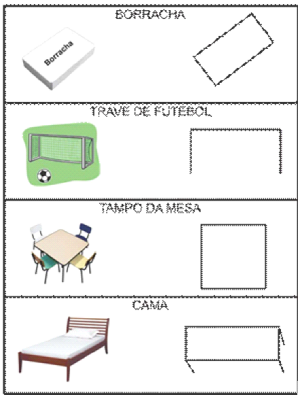
Fonte: Kléber Mendes Vieira (2010)
Figura 3: Representações em contexto de giros limitados
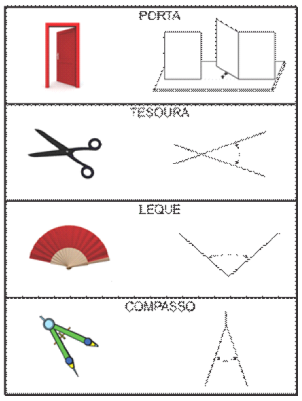
Fonte: Kléber Mendes Vieira (2010)
Figura 4: Representações em contexto de giros ilimitados
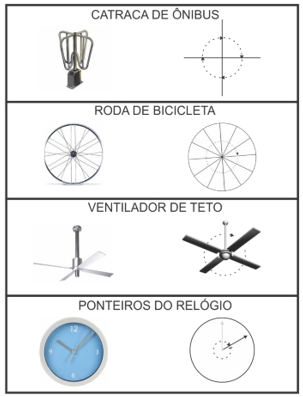
Fonte: Kléber Mendes Vieira (2010)
TEORIA APOS DE ED DUBINSKY
Introdução
Pesquisas mostram que estudantes universitários apresentam dificuldades quando aprendem conceitos abstratos como espaço vetorial, transformação linear, bases, derivadas, entre outros. Estudos realizados em diversos países, procuram desenvolver propostas didáticas com o objetivo de ajudar os estudantes a transporem os obstáculos detectados. A teoria APOS (actions, processes, objects, schemas) vem sendo utilizada por pesquisadores como meio para conhecer as dificuldades dos alunos com os conceitos matemáticos do ensino superior e analisar as construções mentais utilizadas na aprendizagem desses conceitos, além de propor atividades de ensino que contribuam para a compreensão dos conceitos.
A teoria APOS foi desenvolvida por Dubinsky et al. (2000) e surgiu de suas tentativas de estender as ideias de Piaget sobre abstração reflexiva, que descreve o pensamento lógico de crianças, para o nível da aprendizagem matemática na graduação, onde são estudados conceitos matemáticos mais complexos e avançados.
Dentro desta visão, Dubinsky parte da distinção feita por Piaget que inclui três tipos de abstração: a abstração empírica, a abstração pseudo-empírica e a abstração reflexiva. Na abstração empírica o indivíduo observa uma quantidade de objetos e abstrai uma propriedade comum a eles. Na abstração pseudo-empírica o sujeito abstrai a propriedade após as ações que realiza sobre os objetos. A abstração reflexiva interioriza e coordena estas ações para formar novas ações e por fim novos objetos (como uma função, por exemplo). A abstração empírica extrai dados destes novos objetos através de ações mentais sobre eles e assim por diante.
Dubinsky se baseia nas teorias da construção cognitiva desenvolvidas por Piaget e descreve como as ações são interiorizadas em processos e depois encapsuladas como objetos mentais, formando assim, estruturas cognitivas mais sofisticas chamadas esquemas. De uma forma resumida, Dubinsky (1991) define a abstração reflexiva como a construção de objetos mentais por meio de ações mentais do indivíduo sobre estes objetos. A teoria de Dubinsky baseia-se na hipótese de que o conhecimento matemático consiste numa tendência do indivíduo de lidar com situações-problema, através da construção mental de ações, processos e objetos e de organizá-las em esquemas que façam sentido e que permitam resolver os problemas. É uma forma de compreender o modo como os estudantes constroem os conceitos matemáticos e assim entender a origem de muitas dificuldades de aprendizagem.
O modelo cognitivo APOS, se baseia nas ações, processos, objetos e esquemas, chamados de estruturas mentais, que cada indivíduo realiza sobre os conceitos matemáticos que aprende e os mecanismos mentais de abstração reflexiva que são a interiorização, coordenação, encapsulação, generalização e reversibilidade (esta última não faz parte da teoria de abstração reflexiva de Piaget, mas foi incluída por Dubinsky). A interação entre as estruturas e os mecanismos para a construção do conhecimento matemático começa a partir de manipulação de objetos físicos ou abstratos para formar ações. As ações são então interiorizadas para formar processos, os quais são então encapsulados para formar objetos. Os objetos podem ser desencapsulados e voltar a serem processos dos quais eles foram formados. Finalmente, ações, processos e objetos podem ser organizados em esquemas.
Dizemos que ocorreu uma interiorização de uma ação quando o indivíduo é capaz de dar sentido aos seus entendimentos a partir das ações implementadas e de representá-los por símbolos, linguagens e imagens. A coordenação aparece em situações que envolvem a composição ou coordenação de dois ou mais processos para construir um novo. A encapsulação ocorre quando um processo (dinâmico) se torna num objeto (estático). A generalização ocorre quando um indivíduo aprende a aplicar um esquema existente a uma vasta coleção de fenômenos, podendo dizer que o esquema foi generalizado. E, por último, a reversibilidade acontece uma vez que o processo que é existente internamente para o sujeito, ele pode pensar ao contrário, no sentido de construir um novo processo que consiste em inverter o processo original. O quadro abaixo, projetado por Dubinsky, descreve de forma representativa o processo descrito.
Quadro 2: Processo – Teoria APOS
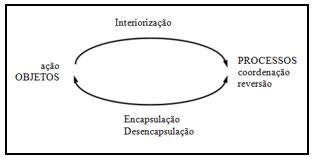
Na Teoria APOS é necessário fazer uma decomposição genética do conceito em questão. Essa decomposição, que não é única, consiste em fazer uma descrição idealizada e detalhada das ações, processos, objetos, esquemas e suas relações que ocorrem na construção de um conceito. A partir dos resultados da análise dos dados obtidos por meio de um teste empírico, a viabilidade da decomposição genética pode ser refinada de modo a oferecer uma melhor descrição da forma como os estudantes constroem o conceito. Será abordado um exemplo com o objetivo de dar uma ideia geral de como poderia funcionar a teria APOS para o ensino de espaços gerados e conjuntos geradores da Álgebra Linear. Neste caso, podemos propor a seguinte decomposição genética: espaço vetorial (os alunos devem reconhecer alguns espaços vetoriais como o conjunto dos Reais, o , o
, as matrizes e os polinômios), variáveis (os alunos devem entender as variáveis como objetos matemáticos, isto é, incógnitas, números quaisquer ou parâmetros) e conjunto de soluções para um sistema de equações (os alunos devem demonstrar uma concepção de objeto desse conceito, isto é, serem capazes de descrever geometricamente a solução do sistema e escrevê-la na forma paramétrica). O Quadro abaixo resume as sugestões de indicadores na identificação da concepção (ação, processo, objeto, esquema) de um indivíduo sobre o conceito de espaços vetoriais.
Quadro 3: Sugestão de indicadores na identificação da concepção
Ação Dados um espaço vetorial V, um conjunto S de vetores de V e um corpo K, as ações consistem em realizar produtos escalares e somas de vetores de S para obter um vetor de V. As coordenações das ações são interiorizadas no processo de construção de combinações lineares. Processo O processo de verificar se existem escalares em K de modo que se possa escrever os elementos de T (um novo conjunto de vetores do espaço vetorial V) como combinação linear dos vetores de S, se coordena no processo de resolução de um sistema de equações, onde as variáveis são os escalares. Através das combinações lineares desses escalares e os vetores de S, é possível verificar se S gera T. Objeto Quando o aluno entende o significado do conjunto S, este processo é encapsulado como um objeto e S é chamado conjunto gerador. Nesta fase, o aluno já percebe que o conjunto gerador não é único e que conjuntos geradores diferentes podem ter quantidades diferentes de elementos. Esquema O estudante tem um esquema para espaços gerados e conjunto gerador, quando esse conceito pode ser invocado e usado em situações-problema da Matemática.
TEORIA DA ABSTRAÇÃO SITUADA POR RICHARD NOSS E CELIA HOYLES
Introdução
Existe uma tensão entre os diferentes discursos da Matemática e o processo mental de aprendizagem. Por um lado, temos a Matemática como objeto, a Matemática per se e por outro e a Matemática como ferramenta, voltada para as práticas culturais. Os estudos de Noss e Hoyles mostram que as tecnologias digitais podem desempenhar um papel muito poderoso para compreender e reformular a natureza do sentido matemático. Esses resultados abrem caminhos para a geração de sentido na aprendizagem da matemática e encoraja a investigar o problema do significado matemático na perspectiva tanto da cognição quanto dos aspectos sociais. Muitos fenômenos referentes ao significado matemático são moldados e estruturados pelas relações culturais e sociais entre as pessoas e suas comunidades, entretanto, isso não invalida o reconhecimento de que muitas facetas do pensamento humano são distantes do social.
Embasamento teórico
A abstração é um tema central para a matemática. Mas, o que é abstração? Robert & Schwarzenberger (1991) descrevem a abstração como envolvendo o reconhecimento de objetos e propriedades que não se aplicam apenas aos objetos dos quais é feita uma generalização, mas também a qualquer outro objeto que obedece às mesmas propriedades. Dreyfus (1991) sugere que a abstração compreende uma mudança de atenção envolvendo reconstrução mental, após a qual as relações entre objetos se tornam centrais. Dubinsky elabora a noção de abstração reflexiva isolando cinco fases neste processo: interiorização, coordenação, encapsulamento, generalização e reversão (Dubinsky, 1991, p. 103).
Noss e Hoyles não veem a abstração como ascensão ou perda de significado e, seguindo Wilensky e outros, propuseram a noção de abstração como um processo de conexão a novos objetos, um processo que se desenvolve em atividade: abstraindo em um domínio e não longe dele. O trabalho de Brown et al. (1989) reconhecia que ensino e cognição são situados, e os trabalhos de Carraher e Schliemann (2002), Sfard (2001), Nemirovsky, Hershkowitz, Schwarz e Dreyfus (2001), abordam como o conhecimento matemático é usado ou “transferido” em configurações. O estudo do conhecimento que emerge da prática laboral também tem sido executado por muitos pesquisadores (ver, por exemplo, o trabalho inspirador de Scribner, 1984, 1986, 1988 e Cole, 1996). Em termos específicos de conhecimento matemático, Noss e Hoyles trabalham há alguns anos objetivando refinar e elaborar suas ideias sobre a natureza da abstração (ver, por exemplo, Noss & Hoyles, 1996). Inicialmente a ideia era caracterizar as formas com que os alunos desenvolviam e expressavam a matemática quando estavam trabalhando em ambientes computacionais, focalizando assim o discurso da aprendizagem. Por outro lado, Resnick (1991) afirmou que “todo ato cognitivo deve ser visto como uma resposta específica a um conjunto específico de circunstâncias” (p.2), limitando a abstração matemática e a cognição situada, colocando esta última numa espécie de beco sem saída para o ensino da matemática. Esse discurso, então, abriu caminhos para outros questionamentos, pois, parece à primeira vista, que matemática perderá todo sentido se não puder, por meios próprios de representação, contextualizar as mais diversas situações. A noção de abstração situada procura descrever como o conhecimento matemático, que é aprendido, discutido e comunicado dentro de uma prática cultural, pode ser situado e abstrato.
Aspectos gerais da teoria
A matemática é frequentemente vista como descontextualizada, não situada e distante da linguagem oficial devido ao seu uso de símbolos e de manipulações algébricas. Uma das intenções da abstração situada é dar um passo para tentar retirar da matemática uma visão descabida de inutilidade. Em vez de pensar na abstração matemática como um afastamento de um referente real e uma focalização em relacionamentos envolvendo objetos e operações matemáticas sem referência, Noss e Hoyles postularam um mecanismo que envolve a abstração dentro da situação e não longe dela. Um exemplo disso é que esses pesquisadores, como relatado em seus diversos artigos, procuram saber como a epistemologia matemática é encontrada no trabalho e assim entender como a matemática é moldada em suas práticas culturais.
Aspectos específicos da teoria
A abstração pode ser vista como o conhecimento organizado em camadas conectadas umas às outras por meio das formas de saber e ver, ao invés de pensarmos como uma forma de substituição de um tipo de significado por outro. O ponto aqui é que esse processo pode acontecer de forma bastante adequada em mundos computacionais. Em tais configurações (mas não apenas em tais configurações) significados são simultaneamente preservados e estendidos no processo construtivo. Esses significados são remodelados à medida que os alunos exploram as ferramentas disponíveis em um domínio onde a abstração surge naturalmente, movendo o foco de sua atenção em novos objetos e relacionamentos. Enfatiza-se o significado da abstração situada como um processo e como um objeto. Isso nos permite usar a palavra “abstração” como aquela que contém as noções de ação, processo ou estado: a abstração situada não é uma coisa por conta própria, é simultaneamente uma “articulação”, uma “declaração”, um (re) pensamento-em-progresso.
Exemplo de aplicação da teoria
Nunes, Schliemann e Carraher (1993) mostram de forma convincente como os vendedores ambulantes, mesmo dentro de uma situação específica e com esquemas pragmáticos da matemática de rua, poderiam generalizar seus conhecimentos de forma flexível. O estudo do uso do conhecimento matemático durante a prática laboral pode contribuir para a construção do significado matemático dentro e, quem sabe, fora dessas configurações. Os significados extraídos das experiências em situações cotidianas, são mais flexíveis, generalizáveis e permitem que as pessoas o mantenham aceso, enquanto que os algoritmos são facilmente esquecidos. O exemplo que abordaremos é sobre o uso do conhecimento matemático (razão e proporção) praticado por enfermeiras pediátricas e foi publicado por Noss e Holyes no artigo Mathematical Epistemologies at Work (2002). Eles observaram como as enfermeiras calculavam as concentrações dos medicamentos em suas práticas diárias e fizeram entrevistas com esses profissionais com o intuito de entender melhor seus conhecimentos obtidos culturalmente e as aplicações desses conhecimentos em outras situações.
Dentro das perspectivas de cálculo de concentração de vários tipos de medicamentos em diversos graus de dificuldades, eles puderam observar os cálculos proporcionais sendo feitos pelas estratégias funcionais, que são abordagens algorítmicas tradicionais, e sendo feitos de forma escalar, que são derivados de experiências cotidianas. Por exemplo, para fazer o cálculo de doses de medicamentos os profissionais usavam o que chamavam de “mantra da enfermagem”. Funcionava como uma versão da regra de três e diz: “o que você quer sobre o que você tem, vezes o valor que vem”. “O que você quer” representa a dose prescrita para o paciente, “o que você tem” é a massa descrita na embalagem do medicamento e “o valor que vem” é o volume discriminado também na embalagem. Outro caso foi mostrado por uma das entrevistadas que tinha um método próprio para esse cálculo. Ela transformava a massa de uma dose em volume apenas com uma conta de multiplicação. Essa regra só funcionava para amicacina (um tipo de antibiótico). A interpretação dos autores é que este conhecimento está ancorado na experiência dessa enfermeira, por fazer muitas vezes as manipulações e cálculos com esse tipo de fármaco. É claro que na literatura isto não faz o menor sentido. O conhecimento foi mutuamente constituído e expresso como a relação entre a matemática e o conhecimento que suas experiências lhe proporcionam.
Uma outra questão foi saber se a abstração situada “transferia” o conhecimento. Para tanto, a estratégia foi deslocar os enfermeiros da sua prática familiar, “forçando-os” a refletir e articular seus conhecimentos adquiridos na teoria com os conhecimentos adquiridos durante a prática no trabalho. Foram feitas uma serie de tarefas e entrevistas, nas quais as enfermeiras foram confrontadas progressivamente com situações que estavam mais longe das práticas observadas, mas ainda mantendo elementos familiares. O resultado foi que quando esses profissionais estavam em simulações fechadas em suas práticas, mantiveram um raciocínio mesclando o os conhecimentos matemáticos que aprenderam na escola com aqueles de suas experiências práticas. Havia um entendimento das relações entre massa, volume, concentração e fração, e assim desenvolveram estratégias de forma a estabelecer uma conexão direta com os artefatos de suas práticas. O contraste aconteceu quando estavam em frente à um cenário não muito familiar. As respostas passaram a não ser muito claras. A conclusão de Noss e Holyes foi que os enfermeiros necessitavam de atividades matemáticas que contivessem questões relacionadas às suas práticas. Quando isso não acontecia os conhecimentos construídos mutuamente pela teoria e a prática ficavam desconectados. Conclui-se que a experiência obtida na prática é um dos núcleos da abstração situada e este tipo de abstração pode “transferir” o conhecimento matemático quando estamos imersos em ambientes ligados à essa prática.
COMPARAÇÕES ENTRE AS TEORIAS
A partir de agora faço minhas considerações sobre as teorias da abstração pseudo-empírica de Mitchelmore & White, da Teoria APOS de Dubinsky e da abstração situada de Noss & Hoyles. Classifiquei essas considerações em três tipos: convergências, quando as teorias compartilham algo em comum, divergências, quando os entendimentos são opostos e as particularidades, quando exponho algo caraterístico ou alguma limitação da teoria. Para uma melhor exposição das ideias, fiz as colocações em forma de tópicos.
Convergências:
- A três teorias são de cunho construtivista, isto é, respeitam a autonomia do indivíduo.
- Em todas as teorias, a abstração não é entendida como um produto, mas sim como ação, interação, processo, isto é, como um verbo.
- As teorias de Mitchelmore & White e de Dubinsky estão de acordo com a abstração reflexiva de Piaget enquanto Noss & Hoyles aceitam essa teoria em parte, pois a mesma não considera a cognição matemática.
Divergências:
- A teoria de Mitchelmore & White promove a aprendizagem de forma deliberada, enquanto a teoria de Noss & Hoyles promove a aprendizagem de forma não intencional.
- As teorias de Mitchelmore & White e de Dubinsky não levam em conta a cognição, diferentemente a teoria de Noss & Hoyles.
- A abstração reflexiva reconhece que as ações nos objetos são refletidas e projetadas no plano do pensamento, que se tornam em uma nova estrutura a partir da reconstrução da antiga. Na abstração situada os significados são simultaneamente preservados e estendidos a novos objetos.
- A teoria de Dubinsky considera uma abstração como contendo alguma propriedade essencial de uma situação extraída dela e não contida nela, enquanto a teoria de Noss & Hoyles pensa na abstração como atividade embutida na situação.
- A teoria de Noss & Hoyles pode ser aplicada em pesquisas da educação matemática tanto para crianças quanto para adultos enquanto a teoria de Mitchelmore & White foi essencialmente projetada para o ensino de crianças.
- A teoria de Dubinsky considera a abstração acontecendo em espirais, como níveis crescentes de abstração, enquanto a teoria da abstração situada de Noss & Hoyles não acredita nessa ideia.
Particularidades:
- A teoria da abstração situada me pareceu limitada em alguns pontos. O conhecimento obtido por meio das práticas culturais é um dos pilares da abstração situada. Provocamos limitações nesta teoria quando tentamos aplicar os conhecimentos matemáticos nas configurações afastadas dessas práticas. De fato, este tipo de abstração pode “transferir” o conhecimento matemático quando estamos imersos em ambientes ligados à essa prática. Fora desses ambientes a teoria não funciona.
- A teoria de Mitchelmore & White estuda as características subjacentes aos objetos e aplica essa teoria aos conceitos da matemática elementar, nas experiências com crianças.
- A teoria de Dubinsky é voltada para entender o que ocorre na mente do indivíduo quando estuda a matemática de nível superior. Relaciona-se então com adultos.
BIBLIOGRAFIA
Mitchelmore, M. C., & White, P. (2000): Teaching for Abstraction: Reconstructing Constructivism. MERGA23,432-439.
Mitchelmore, M. C., & White, P (2000): Development of angle concepts by progressive abstraction and generalisation. Educational Studies in Mathematics, v. 41, n. 3, p. 209-238.
Vieira, Kléber Mendes. O ensino do conceito de ângulo: limites e possibilidades; Kléber Mendes Vieira; 2010.
Domingos, António. Teorias cognitivas e aprendizagem de conceitos matemáticos avançados. Seminário de Investigação em Educação Matemática, v. 17, p. 51-81.
Arnon, I., Cottrill, J., Dubinsky, E., Oktac, A., Roa Fuentes, S., Trigueros, M., & Weller, K. (2013). APOS Theory: A framework for research and curriculum development in mathematics education. New York: Springer.
Kú, D., Oktac¸ , A., & Trigueros, M. (2011). Spanning set and span: An analysis of the mental constructions of undergraduate students. In S. Brown, S. Larsen, K. Marrongelle, & M. Oehrtman (Eds.), Proceedings of the 14th annual conference on research in undergraduate mathematics education, Vol. 1 Portland, OR, (pp. 176–186).
Rachelli, Janice; Compreensão dos conceitos de derivada clássica e derivada fraca: análise segundo o modelo cognitivo APOS; Encontro Brasileiro de Estudantes de Pós-Graduação em Educação Matemática; 20ª Edição.
Noss, R. (2002). Mathematical Epistemologies at Work. For the Learning of Mathematics 22, p. 2-13.
Noss, R, & Hoyles, C. (1996). Windows On Mathematical Meanings: Learning Cultures And Computers. Kluwer Academic Publishers.
