REGISTRO DOI: 10.69849/revistaft/dt10202508270903
Marcos Pereira Magalhães1
ABSTRACT
This article introduces a novel theoretical framework in which spatial connection is governed by non-temporal resonance rather than chronological causality. Based on the concept of trigonotelary geometry, we propose a harmonic field function that connects distant spatial points through a fourth-dimensional entanglement parameter, Θ. The function T(P, Θ) defines spatial relationships based on phase alignment and structural resonance, allowing for ontological simultaneity — a condition in which distinct positions share identical functional states. Unlike conventional space time metrics, this model implies instantaneous transitions between resonant nodes, independent of trajectory or elapsed time. We derive the mathematical properties of the trigonotelary function and demonstrate its implications for topology, causality, and system complexity. This approach opens new possibilities for understanding non-locality in physics and historical processes. The resulting formulation challenges traditional models of spatial continuity, replacing geometric proximity with harmonic identity.
KEYWORDS: Ontology of time, Entropy, Functional identity, Topology, Spacetime.
RESUMO
Este artigo apresenta um novo arcabouço teórico no qual a conexão espacial é governada por ressonância atemporal em vez de causalidade cronológica. Com base no conceito de geometria trigonométrica, propomos uma função de campo harmônica que conecta pontos espaciais distantes por meio de um parâmetro de emaranhamento quadrimensional, Θ. A função T(Θ, Θ) define relações espaciais com base no alinhamento de fase e na ressonância estrutural, permitindo a simultaneidade ontológica — uma condição na qual posições distintas compartilham estados funcionais idênticos. Diferentemente das métricas espaço-temporais convencionais, este modelo implica transições instantâneas entre nós ressonantes, independentemente da trajetória ou do tempo. Derivamos as propriedades matemáticas da função trigonométrica e demonstramos suas implicações para a topologia, causalidade e complexidade do sistema. Essa abordagem abre novas possibilidades para a compreensão da não localidade na física e em processos históricos. A formulação resultante desafia os modelos tradicionais de continuidade espacial, substituindo a proximidade geométrica pela identidade harmônica.
PALAVRAS-CHAVE: Ontologia do tempo, Entropia, Identidade funcional, Topologia, Espaço-tempo.
INTRODUCTION
The paradigm of locality, grounded in the space-time separation of bodies and events, imposes physical limits on movement. This article questions, both conceptually and structurally, several classical foundations of physics, particularly those embedded in the paradigm of relativity and causal locality. The proposed model aims to eliminate time as a parameter and to present the possibility of instantaneous transport between two spatial points. This directly challenges the structure of both special and general relativity, which impose a fundamental speed limit for the propagation of any physical interaction (the speed of light) and require continuity in space-time. In essence, the model seeks to propose a solution that contradicts the continuous and metric nature of space-time and its causal velocity limitations.
This model incorporates a four-dimensional framework not as an independent temporal axis, but as an emergent relational structure embedded within the spatial field. The entanglement parameter, denoted by Θ, acts as a modulator of harmonic resonance between spatial coordinates. Instead of measuring sequential change over time, Θ governs the synchronization of phase states across distant points, enabling a form of ontological simultaneity. In this sense, the fourth dimension manifests through the structure of the field itself — as a dynamic topology shaped by resonance, not chronology. The Trigonotelary Function thus integrates this dimension intrinsically, allowing connectivity to arise from harmonic identity rather than geometric proximity or temporal succession. Recent developments in the study of topological effects and symmetry in solid-state systems offer relevant analogies to our approach, particularly in how phase structure governs connectivity and propagation [1,2].
Thus, in the developed model, space is no longer measured by distance (metric), but by functional equivalence expressed by the Trigonotelar Function, which synthesizes a four-dimensional non linear trigonometric structure. The notion that two points may be functionally ‘adjacent’ despite being spatially distant contradicts the classical view of continuous three-dimensional space, challenging Euclidean/Riemannian geometry and the standard topology based on metric neighborhoods. Furthermore, by adopting the concept of ‘ontological simultaneity’ as defined by the condition T(P₁, Θ) = T(P₂, Θ), with (∂T/∂Θ)|_{Θ = Θₛ} = 0, indicating harmonic equilibrium, it abandons the causal-temporal model of traditional physics and temporal cause effect relationships. However, this contradiction does not imply direct antagonism, as it emerges from an alternative ontological path.
The central hypothesis of this article proposes that it is possible to rigorously model the instantaneous transport of a body between two points, without time acting as a limiting factor. Therefore, we adopt the view that the distance between events is not merely a geometric measurement, but rather an ontological and structural function, potentially eliminable. Thus, we propose the four-dimensional nonlinear trigonometric function, which operates without time as an explicit variable, enabling such a conceptual leap. The complexity of this function incorporates nonconventional mathematical concepts in physics, such as Cantor sets and Perelman’s geometric entropy, to describe spatial connectivity, suggesting that space is a functional web of variable density, as described by Strogatz [3] in his studies on complex networks and continuous spontaneous synchronization. By adopting a view of space as an emergent network of functional topological connections, rather than a fixed stage where events occur, this perspective aligns more closely with complex systems models than with traditional physical frameworks.
THEORETICAL FRAMEWORK AND METHODS
1 – Ontological Simultaneity
The concept of ontological simultaneity, as defined by the condition T(P₁, Θ) = T(P₂, Θ), with (∂T/∂Θ)|_{Θ = Θₛ} = 0, indicating harmonic equilibrium, aligns with Magalhães’s [4] suggestion, when he states that simultaneity can emerge from the internal architecture of systems rather than chronological sequencing. In this framework, events are functionally entangled by their positions within a system’s topological configuration, enabling instantaneous connections beyond traditional space-time constraints.
2 – Perelman’s Geometric Entropy
Perelman’s [5] concept of geometric entropy, developed within the context of Ricci flow and topology, offers a way to evaluate the structural complexity and deformation of manifolds. Applied here, it allows us to understand how regions of space can condense or expand in functional terms, rather than purely geometric ones. This contributes to the notion of spatial equivalence between distant points when viewed through the lens of informational density and entropy minimization.
3 – Cantor Sets
Cantor [6] sets serve as a mathematical foundation for modeling discontinuities and fragmented spaces. Their recursive, self-similar structure allows for the representation of non-continuous spatial domains, which is essential to support the TT function. The presence of “gaps” in Cantor sets parallels the idea of instant disconnection or reconnection between spatial points, forming a lattice of potential equivalences.
4 – Poincaré and Bel
Henri Poincaré’s [7] topological insights, especially concerning the nature of three-dimensional manifolds, provide a framework for understanding global structural transformations in space. Meanwhile, Bell’s [8] theorem from quantum mechanics, which demonstrates the non-locality of entangled particles, reinforces the plausibility of non-local models like the one proposed here. Together, these foundations justify exploring models where distance does not constrain connectivity.
5 – Complex Systems
Complex systems theory provides tools to analyze emergent patterns from non-linear interactions across a network. Such systems are characterized by self-organization, feedback loops, and dynamic equilibrium. In this article, the spatial field is understood as a complex system in which proximity emerges from synchronization and resonance, rather than from geometric measurement [9].
6 – Four-dimensional nonlinear trigonometric function reformulated (Figure 1) To arrive at the Trigonotelary Function, we start with a traditional four-dimensional nonlinear trigonometric function, which explicitly expresses each spatial component and the entanglement parameter:
T(x, y, z, Θ) = ∑ₙ αₙ cos(ωₙₓ·x + ωₙᵧ·y + ωₙz·z + φₙ(Θ))
In this formulation:
– x, y, z ∈ ℝ are spatial coordinates,
– θ ∈ ℝ is the ontological simultaneity (or entanglement) parameter,
– ωₙₓ, ωₙᵧ, ωₙz ∈ ℝ are frequency components along each spatial axis,
– αₙ ∈ ℝ are amplitude coefficients,
– φn(θ)ₙ(θ) is the phase shift modulated by the entanglement parameter.
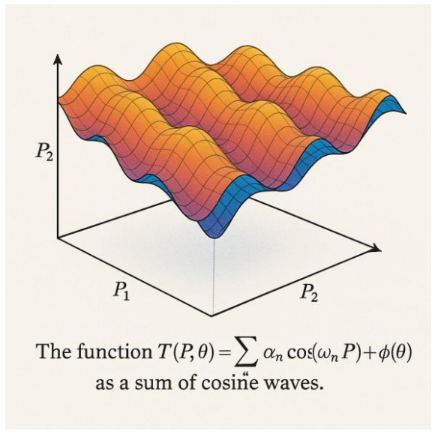
Figure 1 – Trigonotelary function in two dimensions. Graphical representation of the function T(P, Θ) = ∑ₙ αₙ cos(⟨wₙ, P⟩ + φₙ(Θ)), showing a superposition of cosine waves across two spatial dimensions as the entanglement parameter θ varies.
This expression defines a nonlinear oscillatory field over a spatial domain modulated by a fourth ontological dimension, without any reference to time as a fundamental parameter. To generalize this structure and facilitate formal developments in higher-dimensional and topological spaces, we adopt a reformulated notation:
T(P, Θ) = ∑ₙ αₙ cos(⟨wₙ, P⟩ + φₙ(Θ))
Where:
– P = (x, y, z) ∈ ℝ³ is the spatial position vector,
– ωₙ= (ωₙₓ, ωₙᵧ, ωₙz) ∈ ℝ³ is the frequency vector across spatial dimensions,
– θ ∈ ℝ generalizes the entanglement parameter θ,
– ⟨ωₙ, P⟩ denotes the inner product between frequency and position vectors. This vector-based formulation provides a more compact and flexible mathematical framework that serves as the basis for a generalized formalism. In it, the Trigonotelary Function is embedded in a non-Euclidean topological structure, allowing us to describe phase-based equivalences and functional collapses between spatially distant points (Figure 2).

Figure 2 – Multidimensional harmonic network generated by the TT function. Computer-generated rendering showing layered wave networks modulated by the fourth-dimensional parameter θ. The amplitude and frequency variation define topological configurations based on the superposition of harmonic components.
RESULTS
1 – Mathematical Foundations of Key Concepts
Ontological Simultaneity: We define two spatial points P₁ and P₂ as ontologically simultaneous if they satisfy the following conditions under the Trigonotelary Function T(P, Θ): T(P₁, Θ) = T(P₂, Θ) and ∂T/∂θ evaluated at θ = θ* equals zero. This implies that the two points share the same phase output and are in a state of harmonic equilibrium, independent of temporal sequence.
Structural Resonance: Structural resonance occurs when distant spatial points Pᵢ and Pⱼ align phase and frequency components under a common entanglement parameter θ*, such that:
T(Pᵢ, Θ) = T(Pⱼ, Θ) and ∂T/∂Θ(Pᵢ, Θ) = ∂T/∂Θ(Pⱼ, Θ)
This is a generalization of synchronized phase dynamics found in coupled oscillator systems, replacing time with a structural parameter Θ.
Functional Identity: Two points P₁ and P₂ are functionally identical if their values and spatial derivatives under T(P, Θ*) are equal:
T(P₁, Θ⁎) = T(P₂, Θ⁎) and ∇p T(P₁, Θ⁎) = ∇p T(P₂, Θ⁎)
This identity is topological and harmonic rather than geometric.
Ontology of Time: In this model, time is replaced by a structural parameter θ. The function T evolves with respect to θ, and a change in T relative to Θ — expressed as ∂T/∂Θ ≠ 0 — indicates structural evolution. In contrast, in classical models, dX/dt ≠ 0 denotes positional change. Thus, time becomes a derived rather than a fundamental variable (Figure 3).
In summary, based on the formal progression established above—where the TT Function is presented as a compact vector-based structure—we can present the main theoretical results enabled by this framework.
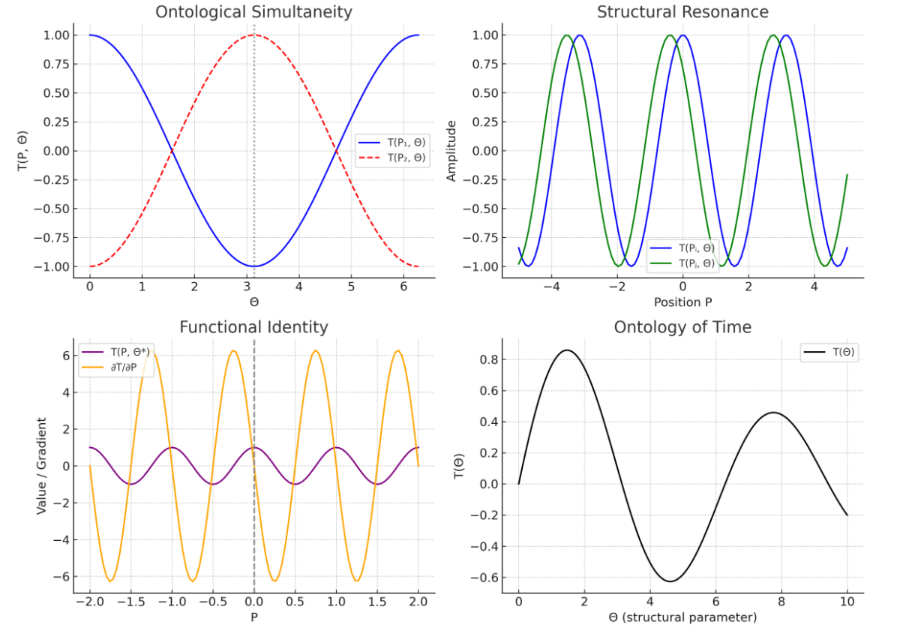
These results focus on the ontological behavior of the function in a non-Euclidean and topologically entangled space, where phase resonance governs the interaction between spatial nodes. Time, in this context, is not a determining variable. Instead, the parameter Θ plays a central role in mediating simultaneity and enabling instantaneous functional equivalence between distinct points.
We begin by formally expressing the TT Function using its generalized formulation. We then introduce the concept of functional collapse, a condition in which spatially distant coordinates become indistinguishable through harmonic identity. Finally, we provide a qualitative and graphical interpretation of the function’s behavior, highlighting zones of resonance, curvature, and entangled topology.
2 – Formalization of the Trigonotelary Function
Based on the reformulated expression already presented, we now adopt the vector-based notation of the Trigonotelary Function as a structural basis for modeling ontological simultaneity and functional equivalence in a non-Euclidean framework:
T(P, Θ) = ∑ₙ αₙ · cos(⟨ωₙ, P⟩ + φₙ(Θ))
Where:
– P ∈ ℝ³ is the spatial position vector, representing the coordinates (x, y, z);
– ωₙ ∈ ℝ³ is the frequency vector associated with each mode n;
– αₙ ∈ ℝ are amplitude coefficients;
– φₙ(Θ) is a phase shift function modulated by the entanglement parameter Θ ∈ ℝ.
Unlike traditional time-based formulations, the TT Function operates within a topological structure where time is not a fundamental parameter. Instead, the function evolves in a space of ontological resonance, governed by phase alignment and spatial-frequency coupling. This model describes a multidimensional oscillatory field in which points are not separated by Euclidean distances but are instead distinguished—or collapsed—based on their phase resonance states. The parameter Θ encapsulates the entanglement or simultaneity structure, functioning as a mediator of functional identity, defined as
T(P₁, Θ⁎) = T(P₂, Θ⁎) and ∇p T(P₁, Θ⁎) = ∇p T(P₂, Θ⁎)
Thus, the TT Function is not merely a spatial wave function, but a resonant phase field where identity between points emerges from harmonic alignment, enabling phenomena such as functional collapse, instantaneous transposition, and topological proximity without geometric contiguity.
3 – Functional Collapse Condition
T(P₍ᵢ₎, Θ₍c₎) = T(P₍ⱼ₎, Θ₍c₎) and (∂T/∂Θ)|_{Θ = Θ₍c₎} = 0 (Eq. 7)
The system reaches a functional collapse (instantaneous equivalence between two distinct spatial points Pᵢ and Pⱼ) when: This critical condition Θ_c corresponds to a phase equilibrium state in which two spatially separated points become indistinguishable under the output of the function. Rather than restating the definition, we refer to the condition of functional identity established above:
T(P₁, Θ⁎) = T(P₂, Θ⁎) and ∇ₚ T(P₁, Θ⁎) = ∇ₚ T(P₂, Θ⁎) (Figure 4).
4 – Graphical Representation and Interpretation (Figure 5)
The TT function generates a multidimensional oscillatory field with locally and globally entangled structures. Under graphical simulations, the TT function reveals: – Dense wave interference zones where the condition of functional identity holds; – Curved propagation patterns that reflect non-metric topology;
– Symmetrical harmonic regions indicating the potential for instant transport between distant nodes.
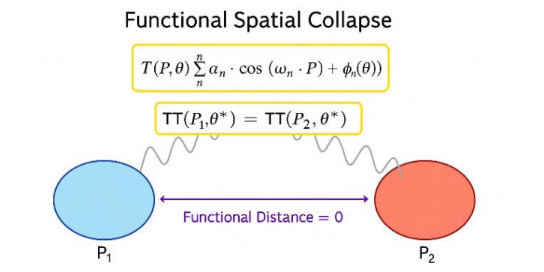
Figure 4 – Functional collapse under entanglement parameter θ*. Schematic diagram illustrating two spatially distinct points (P₁ in blue, P₂ in red) aligned by the TT function. The yellow box marks the state where TT(P₁, Θ⁎) = TT(P₂, Θ⁎), and the purple arrow indicates nullified functional distance at phase equilibrium.

Figure 5 – Entangled mesh generated by phase synchronization. Visualization of the TT field showing continuous spatial curvature and harmonic twisting across dimensions. Phase entanglement modulates structural proximity between nodes, forming a dense network.
These results are consistent with the theoretical condition of ontological proximity: two points sharing the same resonance state are not merely “close” in geometric terms, but effectively collapsed in the functional topology (Figure 6).
Figure 6 – Final configuration of the TT resonant network. Layered representation of TT-based spatial nodes coupled via four-dimensional entanglement. Frequency and orientation modulate the spatial topology under the parameter θ, forming a continuous non-Euclidean harmonic field.
5 – Ballistic Resonance and Graphical Representation This section addresses the conceptual need to visually represent the phenomenon of ballistic movement between two distant spatial coordinates governed by the TT function. In contrast to conventional motion, which involves displacement over time, ballistic resonance in this context refers to the functional collapse that instantaneously aligns two spatial points via harmonic identity. This resonance-based connection is represented topologically rather than geometrically, allowing a direct transposition between distant coordinates without the mediation of velocity or elapsed time. The figure 7 illustrates the four-dimensional framework underlying this model, highlighting the structural transformation enabled by the critical entanglement parameter Θ.
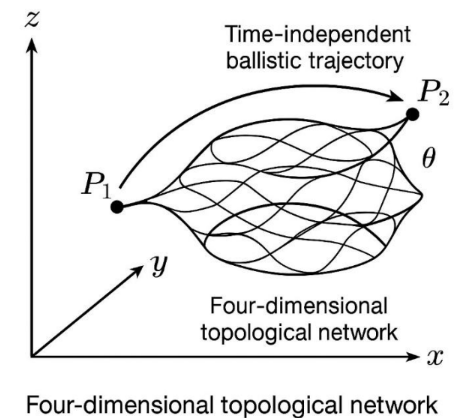
Figure 7 – Schematic diagram of ballistic resonance. The illustration shows a hypothetical four dimensional space in which a point mass transitions between P₁ and P₂ through harmonic identity without temporal propagation. The diagram visualizes ontological simultaneity and functional collapse as conditions of instantaneous spatial transposition governed by the entanglement parameter Θ.
6 – Conceptual Consequences
The formal structure suggests that:
– Space may be emergent from resonance and synchronization patterns; – Distance becomes irrelevant where phase and amplitude conditions align; – Transport is replaced by instantaneous manifestation, challenging classical continuity and relativistic constraints [10].
These insights expand the potential for mathematical and physical exploration of non-local interaction fields in cosmology, quantum information, and historiographical models of structural equivalence.
DISCUSSION
1 – Functional Collapse Condition
The central theoretical result derived from the Trigonotelary Function (TT) is the condition of functional collapse. As established in Section 3, this collapse allows two spatially distinct points
to become functionally equivalent when their respective TT values coincide under a critical entanglement parameter Θₛ:
T(P₁, Θ) = T(P₂, Θ) and (∂T/∂Θ)|_{Θ = Θₛ} = 0
This equation expresses a phase equilibrium where the topological configuration of the space reaches a point of convergence. In this state, the function’s harmonic composition eliminates the spatial separation between P₁ and P₂, causing them to collapse into a single ontological identity within the function’s domain.
This theoretical condition has strong implications: it removes the dependency on metric distance and redefines the notion of connectivity in terms of resonance, frequency, and ontological alignment. It transforms movement from a trajectory to a structural reconfiguration in the phase space defined by the TT function.
2 – Mathematical Representations
The reformulated TT function adopts a compact vector form that facilitates analytical manipulation and visualization:
T(P, Θ) = ∑ₙ αₙ · cos(⟨ωₙ, P⟩ + φₙ(Θ))
This expression supports a variety of dynamic and topological configurations, allowing the generation of multidimensional fields of oscillatory influence.
3 – Analogies with Quantum Experiments
The TT model mirrors quantum entanglement: spatial separation does not prevent instantaneous relational behavior. The critical parameter Θ acts as a tuning variable, aligning distant points as though “entangled.” Practical advances in the generation and control of entangled states, such as broadband optical antennas, reinforce the plausibility of engineered resonant connectivity across domains [11].
Unlike quantum indeterminacy, however, the TT framework is deterministic within its ontological domain, governed by harmonic and phase alignment. This analogy is conceptually valuable for understanding the model’s non‑local simultaneity.
Experimental realizations of high-dimensional entanglement, such as 18-qubit systems entangled across multiple degrees of freedom, underscore the viability of extended resonance topologies as modeled by the TT function [12].
4 – Cosmological and String‑Theoretical Implications
The TT functional mesh resonates with cosmological structures such as the cosmic web, where filaments connecting galaxies can be interpreted as resonance strands. Likewise, string theory’s vibrational paradigm finds an ontological parallel: TT envisions space as a phase‑based field in which resonance, not geometry, dictates spatial identity Similar proposals, such as the black hole bounce hypothesis, suggest alternative ontological conditions for the emergence of structure beyond classical spacetime constraints [13].
Thus, the TT field may be viewed as a macroscopic lattice of ontological “strings” whose interactions define proximity, existence, and manifestation. These interpretations find conceptual alignment with black hole cosmology frameworks, which treat the universe itself as a product of ontological transitions inside black holes [14]. In this context, space itself can be conceived as emerging from the interior geometry of black holes, forming causal structures that do not rely on external spatial expansion [15].
5 – Historical Theory and Structural Equivalence
Beyond physics and cosmology, the TT model offers insights for historiography. If resonance— rather than chronological sequence—governs connectivity, historical events may be structurally equivalent despite temporal or geographic separation.
Modeling history via shared resonance patterns (ontological isomorphism across eras) allows rethinking causality, recurrence, and pattern recognition in structural history, with the TT function providing a formal tool for such analysis.
CONCLUSIONS
This study introduced and formalized the Trigonotelary Function (TT) as a theoretical and mathematical model capable of collapsing spatial distance through harmonic equivalence. The central claim of this work is ontological: the space between two points is not fundamentally defined by metric distance, but by the alignment of resonance, frequency, and phase within a multidimensional functional topology.
Unlike conventional physical models, which rely on geometric continuity and chronological causality, the TT function eliminates time as a fundamental variable and replaces Euclidean separation with functional connectivity. This represents a paradigm shift: from a metric space to a resonant structure; from distance to ontological synchronization.
The notion of functional resonance, expressed through the TT harmonic superposition, allows for the simultaneous manifestation of a body at multiple spatial coordinates when certain conditions are met — notably, the tuning of the entanglement parameter Θ to its critical value, Θ_c. This functional identity, in which both the value and the spatial gradient of T coincide at two distinct spatial points under this condition, defines a topological state where spatial separation becomes irrelevant to localization.
Moreover, the TT model suggests that space is not a container but a dynamic mesh of relational intensities. In this mesh, proximity is determined not by position but by phase, and causality emerges from structural equivalence rather than sequential ordering. This ontological perspective opens new possibilities not only for theoretical physics and cosmology but also for historiography, where structural resonance — interpreted mathematically as the phase alignment T(Pᵢ, Θ) = T(Pⱼ, Θ) and the equivalence of partial derivatives ∂T/∂Θ at those points — allows distinct historical events or sites to be treated as topologically connected when they share the same functional output and entanglement condition.
In essence, the Trigonotelary Function redefines spatiality and presence. It introduces a non metric, non-temporal substrate of reality governed by phase resonance — a continuous field where equivalence precedes separation, and manifestation replaces motion. It is a move toward a physics of relational presence, encoded in the harmonics of a multidimensional space.
REFERENCES
1. ZHANG, H. & LI, X. Topological protection in two-dimensional quantum materials. npj 2D Mater. Appl. 9, 1 (2025).
2. GONZALEZ, A. & KRÄMER, J. Computational models of entanglement propagation in topological lattices. Comput. Phys. Commun. 305, 109349 (2024).
3. STROGATZ, SH. Sync: The emerging science of spontaneous order. New York: Hyperion 2003. 4. MAGALHÃES, MP. A simultaneidade generalizada dos acontecimentos. In: MAGALHÃES, MP, ed. Amazônia Antropogênica. Belém (PA): Museu Paraense Emílio Goeldi; 2016, pp. 45–91. 5. PERELMAN, G. The entropy formula for the Ricci flow and its geometric applications. arXiv 2002, arXiv:math/0211159. https://arxiv.org/abs/math/0211159
6. CANTOR, G. Contributions to the founding of the theory of transfinite numbers. New York: Dover, 1955.
7. POINCARÉ, H. Analysis situs. J. Éc. Polytech. 1895, 10, 1–123.
8. BELL, JS. On the Einstein Podolsky Rosen paradox. Physics 1964, 1(3), 195–200. 9. WATTS, DJ, STROGATZ, SH. Collective dynamics of “small-world” networks. Nature. 1998;393(6684):440–442. https://doi.org/10.1038/30918
10. POPŁAWSKI, NJ. Cosmology with torsion: An alternative to cosmic inflation. Phys Lett B. 2010;694(3):181–185. https://doi.org/10.1016/j.physletb.2010.09.056
11. CHEN, Y; ZHANG, Y; WANG, X; ZHANG, W; LI, J. Efficient extraction of entangled photons using a broadband optical antenna. Nat Commun. 2018;9:2994. https://doi.org/10.1038/s41467- 018-05362-9
12. WANG, X-L; LUO, Y-H; HUANG, H-L. et al. 18-Qubit Entanglement with Six Photons’ Three Degrees of Freedom. Phys Rev Lett. 2018;120:260502. https://doi.org/10.1103/PhysRevLett.120.260502
13. AFSHORDI, N; MANN, RB; POURHASAN, B. The Black Hole Bounce: A New Perspective on Cosmological Initial Conditions. J Cosmol Astropart Phys. 2015;2015(04):001. https://doi.org/10.1088/1475-7516/2015/04/001
14. HAMILTON-MORRIS, A; LASHER, A; AFSHORDI, N. Observational tests of black hole cosmology. arXiv preprint. 2024. https://arxiv.org/abs/2401.12962
15. POPŁAWSKI, NJ. Universe in a black hole with torsion. Gen Relativ Gravit. 2019;51:123. https://doi.org/10.1007/s10714-019-2624-8
1Museu Paraense Emílio Goeldi, Belém, PA, Brasil. mpm@museu-goeldi.br
https://orcid.org/0000-0003-1711-8235
