PO-SHEN LOH’S METHOD AS A DIDACTIC ALTERNATIVE IN SOLVING QUADRATIC EQUATIONS: AN APPLICATION PROPOSAL FOR THE 9TH GRADE OF BASIC EDUCATION IN ANGOLA
REGISTRO DOI: 10.69849/revistaft/dt10202507090958
Inácio Miguel Gabriel1
Boaventura Beleza dos Santos Nolasco2
RESUMO
Este artigo apresenta uma proposta alternativa para a resolução de equações quadráticas, com base no método desenvolvido por Po-Shen Loh, direcionada ao ensino da 9ª classe do I Ciclo do Ensino Secundário em Angola (ensino fundamental). O estudo parte do reconhecimento de que o ensino tradicional se reduz principalmente à utilização da fórmula resolvente (Bhaskara), o que pode limitar a compreensão conceitual e a motivação dos alunos. A investigação envolveu 26 professores de Matemática de cinco escolas da cidade do Lubango (Angola) e cinco professores peritos, com o objetivo de avaliar a viabilidade didática e pedagógica da proposta. A metodologia adotada foi de natureza descritiva, com abordagem quali-quantitativa. Os dados revelam que a maioria dos professores considera o método de Po-Shen Loh compreensível, acessível e potencialmente motivador, pois oferece uma abordagem lógica que dispensa a memorização formal de fórmulas. A proposta é apresentada com um esquema próprio e exemplo de aplicação. Conclui-se que o método constitui uma alternativa válida para enriquecer o processo de ensino e aprendizagem de equações quadráticas, promovendo a aprendizagem significativa.
Palavras-chave: equações quadráticas; ensino de Matemática; método de Po-Shen Loh; aprendizagem significativa; I ciclo do ensino secundário.
ABSTRACT
This article presents an alternative proposal for solving quadratic equations, based on the method developed by Po-Shen Loh, aimed at teaching 9th grade students in the First Cycle of Secondary Education in Angola (basic education). The study starts from the recognition that traditional teaching is mainly reduced to the use of the quadratic formula (Bhaskara), which may limit students’ conceptual understanding and motivation. The research involved 26 Mathematics teachers from five schools in the city of Lubango (Angola) and five expert teachers, with the aim of evaluating the didactic and pedagogical feasibility of the proposal. The adopted methodology was descriptive, with a qualitative quantitative approach. The data reveal that most teachers consider Po-Shen Loh’s method understandable, accessible, and potentially motivating, as it offers a logical approach that eliminates the need for formal memorization of formulas. The proposal is presented with its own scheme and an application example. It is concluded that the method constitutes a valid alternative to enrich the teaching and learning process of quadratic equations, promoting meaningful learning.
Keywords: quadratic equations; Mathematics teaching; Po-Shen Loh’s method; meaningful learning; first cycle of secondary education.
1. INTRODUÇÃO
O ensino da Matemática continua a representar um desafio significativo em diversos níveis de escolaridade, particularmente no que diz respeito ao desenvolvimento do pensamento algébrico e à resolução de equações. Em muitos contextos escolares, inclusive no sistema educativo angolano, os conteúdos relativos às equações quadráticas são abordados de forma mecânica, com ênfase quase exclusiva na aplicação da fórmula resolvente (Bhaskara). Esse modelo de ensino, centrado na repetição de fórmulas, pode limitar a compreensão conceitual dos alunos e reduzir sua motivação para a aprendizagem da Matemática. Como enfatiza Vale (2008), o processo de abstração matemática é sustentado pela experiência concreta, sendo fundamental criar pontes entre a prática e a teoria para facilitar a aprendizagem.
Nesse sentido, estratégias de ensino, como sugere Micombero (2016), também contribuem para o envolvimento ativo dos alunos e a construção reflexiva do conhecimento. A aprendizagem significativa, conforme defendida por Ausubel (1963) e Piaget (1977), exige a conexão entre o conhecimento prévio e os novos conteúdos, permitindo ao aluno atribuir sentido ao que aprende. Isso pressupõe a oferta de estratégias didáticas diversificadas que respeitem os diferentes estilos cognitivos e promovam a construção ativa do conhecimento. Nesse contexto, a introdução de métodos alternativos de resolução de equações quadráticas pode representar uma estratégia valiosa para ampliar o repertório matemático dos alunos e promover a autonomia intelectual.
Além disso, conforme argumenta Flóes (2012), o uso de estratégias heurísticas pode fortalecer o papel do professor como mediador de uma aprendizagem mais contextualizada e significativa. Este artigo tem como objetivo apresentar uma proposta alternativa de resolução de equações quadráticas baseada no método desenvolvido pelo professor Po-Shen Loh (2019), matemático da Carnegie Mellon University. Trata-se de um método que se distingue pela simplicidade lógica e pela acessibilidade, permitindo aos alunos compreenderem a estrutura das soluções sem depender da memorização formal de fórmulas. A proposta foi analisada à luz de dados recolhidos junto de professores da 9ª classe e especialistas em ensino da Matemática, avaliando sua viabilidade, clareza e aplicabilidade no contexto do I ciclo do ensino secundário em Angola.
2. METODOLOGIA
Este estudo caracteriza-se como uma pesquisa de natureza descritiva, com abordagem quali-quantitativa. A vertente qualitativa permitiu analisar as percepções dos docentes quanto à proposta metodológica, enquanto a abordagem quantitativa possibilitou a sistematização estatística dos dados recolhidos.
A investigação foi conduzida de 2021 a 2022, durante o ano letivo regular, em cinco escolas do I ciclo do ensino secundário da cidade do Lubango, província da Huíla (Angola). A amostra foi composta por 26 professores de Matemática que lecionam a 9ª classe, selecionados de forma aleatória simples, além de cinco professores peritos com reconhecida experiência acadêmica e prática no ensino da Matemática (selecionados deterministicamente).
Os dados foram coletados por meio de dois inquéritos estruturados: o primeiro, destinado aos docentes das escolas, visou identificar os métodos tradicionalmente utilizados na resolução de equações quadráticas, bem como as dificuldades enfrentadas pelos alunos nesse conteúdo; o segundo inquérito foi aplicado aos professores peritos, com foco na avaliação da clareza, aplicabilidade e potencial didático do método de Po-Shen Loh como alternativa viável à fórmula resolvente.
A análise dos dados seguiu dois procedimentos complementares: (i) a análise estatística descritiva, baseada no cálculo de frequências absolutas e relativas; e (ii) a análise de conteúdo das respostas abertas, permitindo uma interpretação aprofundada e contextualizada à luz dos objetivos pedagógicos do estudo.
3. PROPOSTA DIDÁTICA
O método de Po-Shen Loh constitui uma abordagem inovadora e alternativa à tradicional fórmula resolvente para a resolução de equações quadráticas da forma geral. Sua originalidade reside no uso da média das raízes e da estrutura simétrica das equações quadráticas, eliminando a necessidade de memorizar fórmulas e promover o raciocínio lógico.
A proposta, conforme desenvolvida nesta investigação, visa aplicar esse método junto aos alunos da 9ª classe, favorecendo uma aprendizagem mais intuitiva e significativa.
3.1. Fundamento do Método
O método de Po-Shen Loh parte da observação de que toda equação quadrática x² + bx + c = 0, pode ser resolvida explorando a simetria entre as raízes. Isto é, em vez de usar a fórmula resolvente, Po-Shen Loh propõe trabalhar com a média das raízes e a distância entre elas.
Considerando a equação quadrática do tipo x² + bx + c = 0, podemos interpretá-la como uma soma e produto de raízes:
(x − x¹)(x − x²) = x² − (x¹ + x²)x + x¹x²
Logo, se soubermos que as raízes têm a soma igual a −b e o produto a c, podemos considerar:
1. A média das raízes como sendo m = −b/2;
2. As raízes são simetricamente distribuídas em torno dessa média: m − u e m + u, donde u é a distância da raiz à média;
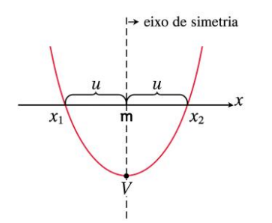
3. O produto das raízes será (m − u)(m + u) = m²− u²= c
Assim, temos:
m² − u² = c ⟹ u² = m² − c
3.2. Passos do Método
Para resolver x² + bx + c = 0:
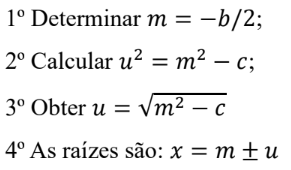
3.2.1. Exemplo resolvido com o método
Seja a equação: x² + 6x + 5 = 0
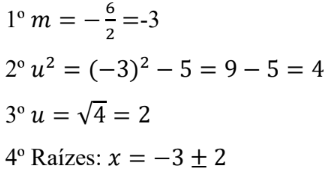
3.3. Vantagens do Método
Destacam-se as principais vantagens:
1. Evita memorização de fórmulas;
2. Estimula o raciocínio lógico e a compreensão estrutural das equações;
3. Favorece a aprendizagem significativa ao integrar conceitos como média, simetria e produto notável.
3.4. Representação Esquemática do Método
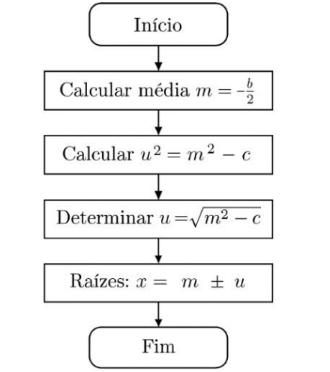
Fonte: A autoria
Este esquema foi testado com os professores participantes da investigação e considerado claro e funcional para introdução em sala de aula.
4. RESULTADOS E DISCUSSÃO
Os resultados obtidos a partir dos inquéritos revelam que a maioria dos professores participantes considera a abordagem tradicional centrada na fórmula resolvente como excessivamente mecanicista e pouco eficaz para promover a compreensão conceitual dos alunos. Dos 26 docentes inquiridos, 84.6% afirmaram que os alunos demonstram dificuldades em compreender a origem da fórmula de Bhaskara e aplicá-la corretamente sem erros operatórios.
Em contraste, o método de Po-Shen Loh foi avaliado como acessível por 92% dos professores, destacando-se por sua estrutura lógica intuitiva. Os docentes reconheceram que o método estimula o raciocínio matemático e permite que os alunos compreendam o processo de resolução de forma mais ativa, em vez de memorizar uma fórmula abstrata ou que se lhes parece abstrata.
Os professores peritos consultados também ressaltaram o valor pedagógico da proposta, considerando-a promissora para o contexto angolano e não só. Apontaram como principais vantagens a sua clareza conceitual, a potencial redução da carga cognitiva e a possibilidade de integrar o método a abordagens por descoberta, alinhando-se às teorias de aprendizagem significativa de Ausubel e às construtivistas de Piaget.
Do ponto de vista didático, o método de Po-Shen Loh pode ser integrado ao currículo como uma alternativa complementar à fórmula resolvente, oferecendo aos alunos mais de uma via de compreensão e resolução das equações quadráticas. A possibilidade de apresentar o método em forma de “descoberta guiada” também foi considerada um diferencial positivo.
Em suma, os dados demonstram que a proposta é bem acolhida pelos profissionais da educação e apresenta fundamentos teóricos e práticos que justificam sua aplicação em sala de aula. A discussão dos resultados permite concluir que a introdução do método de Po-Shen Loh pode contribuir significativamente para a melhoria da aprendizagem das equações quadráticas, ampliando o acervo didático dos professores e favorecendo uma aprendizagem mais significativa por parte dos alunos.
5. CONCLUSÃO
Com base nos dados analisados, conclui-se que o método de Po-Shen Loh representa uma alternativa didaticamente viável e pedagogicamente rica à tradicional fórmula resolvente na abordagem das equações quadráticas. Sua estrutura lógica simples e intuitiva contribui para a compreensão significativa dos conceitos matemáticos, promovendo um ensino menos mecânico e mais reflexivo.
A aceitação majoritária por parte dos professores inquiridos e peritos evidencia o potencial deste método como ferramenta complementar eficaz no contexto do I ciclo do ensino secundário em Angola. Além disso, a proposta está alinhada com abordagens contemporâneas de ensino que valorizam o raciocínio, a descoberta e a participação ativa do aluno no processo de aprendizagem.
Recomenda-se a aplicação experimental do método em contextos reais de sala de aula, bem como a realização de estudos posteriores que envolvam diretamente os alunos, com o objetivo de avaliar o impacto da proposta na aprendizagem efetiva. Tais investigações poderão consolidar a validade pedagógica do método e contribuir para a inovação do ensino de Matemática em Angola e além-fronteiras.
REFERÊNCIAS
AUSUBEL, D. P. The psychology of meaningful verbal learning. New York: Grune & Stratton, 1963.
FILHO, B. B.; SILVA, C. X. da. Matemática: ensino médio. Volume único. Minas Gerais: FTD, 2005.
FLÓES, L. M. Modelagem matemática na formação de professores: o papel das estratégias heurísticas. Maringá: Eduem, 2012.
LOH, P.-S. A new way to solve quadratic equations. The Mathematical Intelligencer, v. 41, p. 1–4, 2019. Disponível em: https://doi.org/10.1007/s00283-019-09926-2.
MICOMBERO, P. O uso de estratégias de ensino no processo de aprendizagem da matemática: uma abordagem centrada na resolução de problemas. Revista Moçambicana de Educação, v. 27, n. 2, p. 55–68, 2016.
PIAGET, J. A equilibração das estruturas cognitivas: problema central do desenvolvimento. Porto Alegre: Artmed, 1977.
VALE, I. Da experiência à abstracção na aprendizagem da matemática. Quadrante, v. 17, n. 1, p. 99–125, 2008.
1Licenciado em Ensino de Matemática pelo Instituto Superior de Ciências de Educação da Huíla – ISCED (Angola). Licenciado em Engenharia de Minas pelo Instituto Superior Politécnico da Huíla (ISPH) da Universidade Mandume Ya Ndemufayo – UMN (Angola). Mestrando em Estatística e Investigação Operacional pela Faculdade de Ciências da Universidade de Lisboa. Mestrando em Educação e Tecnologias Digitais pelo Instituto de Educação da Universidade de Lisboa. Professor do Departamento de Geologia e Minas do ISPH. Professor de Matemática do Colégio José Eduardo dos Santos – Namibe (Angola). Email: imgabriele0@gmail.com /igabriel@isph.umn.ed.ao.
2Professor Doutor em Matemática e Aplicações pela Universidade de Beira Interior (UBI). Professor de Matemática do Instituto Superior de Ciências de Educação da Huíla (Angola). Email: beleza2011@live.com.pt
