PREDICTION OF VAPOR-LIQUID EQUILIBRIUM IN BINARY SYSTEMS USING UNIQUAC MODEL: A COMPARISON BETWEEN THE GENETIC ALGORITHM AND DETERMINISTIC MODELS
REGISTRO DOI: 10.69849/revistaft/ma10202505131408
Samuel Ramos Arruda1
Resumo
O presente trabalho trata da predição do equilíbrio líquido-vapor (ELV) em sistemas binários com a utilização do modelo termodinâmico Universal Quasi-Chemical (UNIQUAC), sendo implementado o método estocástico algoritmo genético (AG) e os métodos determinísticos, Levenberg-Marquardt, Declive máximo e Newton-Raphson para estimar os parâmetros de interação binária presentes. A metodologia foi implementada em MATLAB e aplicada a seis sistemas binários distintos, considerando o modelo gama-phi e o uso de dados experimentais presentes na literatura. A qualidade do ajuste foi avaliada por meio do erro médio relativo (EMR%) e os resultados obtidos mostram que o AG apresenta desempenho competitivo em relação aos métodos determinísticos, devido ao contorno de limitações associadas à escolha de estimativas iniciais e à convergência para mínimos locais.
Palavras-chave: Equilíbrio líquido vapor. Modelos determinísticos. Algoritmo genético. UNIQUAC.
1 INTRODUÇÃO
O equilíbrio líquido-vapor (ELV) é um fenômeno fundamental em diversas operações presentes na engenharia química, com grande variedade em processos industriais, como destilação e extração, sendo vitais para a produção de alimentos e materiais químicos. O equilíbrio líquido-vapor ocorre quando a taxa de evaporação para um dado componente i que está na fase líquida é coincidente com a taxa de condensação para este mesmo componente na fase vapor, em uma mesma temperatura e pressão (AZEVEDO; ALVES, 2017).
O conhecimento preciso das condições de equilíbrio entre fases é essencial para o projeto e a otimização dos equipamentos industriais. De modo geral, as informações são obtidas por meio de dados experimentais, que, embora confiáveis, demandam de recursos. Nesse contexto, a modelagem do equilíbrio de fases em sistemas termodinâmicos desempenha um papel crucial, possibilitando a predição de dados com menor custo experimental.
A modelagem do ELV busca descrever e prever esse fenômeno com precisão, sendo o coeficiente de atividade uma variável indispensável para esse propósito. Modelos termodinâmicos como o Universal Quasi-Chemical (UNIQUAC) utilizam parâmetros de interação binária que variam conforme o tipo de mistura e, geralmente, são ajustados a partir de dados experimentais.
Devido a não-linearidade presente na modelagem matemática, a utilização de modelos matemáticos, como Newton-Raphson, Levenberg-Marquardt e declive máximo, podem enfrentar dificuldades nas estimativas dos parâmetros que tenham convergência para um mínimo local e não em uma solução global, além de que os modelos matemáticos exigem uma boa estimativa inicial, avaliação de gradiente, portanto, sua utilização requer custo computacional.
Com relação às características pertinentes aos modelos matemáticos e suas limitações para a determinação dos parâmetros presente no coeficiente de atividade, em alternativa a estes modelos, para a estimativa dos parâmetros, o uso de métodos de otimização estocástica, como Algoritmo Genético (AG), mesmo que não possua garantia formal para a otimização de solução global, este pode apresentar soluções satisfatórias.
Neste trabalho, é apresentada a aplicação de algoritmo genético (AG) para a estimativa dos parâmetros de interação binária do modelo termodinâmico UNIQUAC e realizada uma comparação com três modelos matemáticos, Newton-Raphson, Levenberg Marquardt e declive máximo, aplicados à modelagem de seis sistemas binários. Desta forma, avalia-se o desempenho da otimização estocástica frente às abordagens clássicas.
2 FUNDAMENTAÇÃO TEÓRICA
2.1 Equilíbrio Líquido-vapor
Na termodinâmica do equilíbrio de fases, estabelecem-se as relações entre propriedades fundamentais dos componentes de um sistema, como temperatura, pressão e composição química. O equilíbrio entre fases é alcançado quando essas propriedades se ajustam de forma que não ocorra transferência de massa ou calor entre as fases, caracterizando um estado estável e contínuo do sistema (AZEVEDO; ALVES, 2017).
O equilíbrio de fases depende de condições a serem verificadas, sendo estes o mecânico, térmico e químico, desta forma, considerando as fases líquida e vapor, tem-se:

O equilíbrio líquido-vapor (ELV) representa uma condição termodinâmica em que as fases líquidas e vapor de uma substância coexistem em equilíbrio, logo, as taxas de evaporação e condensação são iguais, isto para a mesma temperatura e pressão. O potencial químico (u) não possui equivalência de forma imediata, desta forma, para expressar o potencial químico em termos de alguma função auxiliar, sendo denominado fugacidade (f) (PRAUSNITZ; LICHTENTHALER; AZEVÊDO, 1999).
Desse modo, a equação 3 pode ser reescrita em termos de fugacidade, logo, tem se a equação 4.



3 METODOLOGIA
3.1 Seleção de sistemas para estudo, dados e materiais.
Para a seleção dos dados experimentais de equilíbrio líquido-vapor utilizados neste estudo foram obtidos através da coleção Vapor-Liquid Equilibrium Data Collection organizada por Gmehling et al., 1980-1983 os seis sistemas binários devem apresentar as seguintes informações: Fração molar na fase vapor (y), fração molar na fase líquida (x), Pressão, Temperatura e no mínimo 29 dados sobre o experimento.
3.2 Cálculo do modelo gama-phi

Para o cálculo do coeficiente de fugacidade, foi adotado a expansão virial truncada no segundo termo e o coeficiente de fugacidade determinado a partir do modelo Universal
Quasi-Chemical (UNIQUAC). Em relação ao termo em exponencial (fator de Poyting), em baixas pressões e moderadas, possui diferenças milésimas, sua omissão não introduz um erro considerável.
3.2.1 Cálculo do coeficiente de fugacidade

As equações auxiliares para o cálculo do coeficiente de fugacidade são apresentadas no apêndice A.
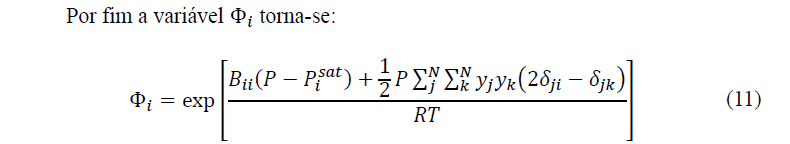
3.2.2 Modelo Universal Quasi-Chemical
O modelo termodinâmico Universal Quasi-Chemical estende a teoria quasi-chemical de Guggenheim, sendo desenvolvido por Abrams e Praunitz. O modelo trata a soma entre as partes combinatória, que representa as diferenças de tamanho e forma molecular, sendo as contribuições entrópicas, e o residual, que trata sobre as interações moleculares, responsáveis pela entalpia presente na mistura (OLIVEIRA, 2003), apresentada na equação 12.


3.3 Modelos matemáticos de predição
Para estimar os parâmetros binários presentes no modelo UNIQUAC, foram empregados três métodos matemáticos determinísticos amplamente utilizados na resolução de problemas de ajuste de parâmetros para equações não lineares: Levenberg Marquardt, Declive máximo, Newton-Raphson. A seguir, descrevem-se os procedimentos adotados para implementação para cada um dos métodos com a função a ser minimizada.
3.3.1 Levenberg-Marquardt
O método de Levenberg-Marquardt é uma técnica iterativa utilizada para minimizar funções de erro quadrático, combinando as vantagens presentes no método de Gauss-Newton e da descida de gradiente. O método é eficaz em problemas onde a matriz Hessiana pode ser mal condicionada ou singular. Sendo a Equação, que representa o resíduo.
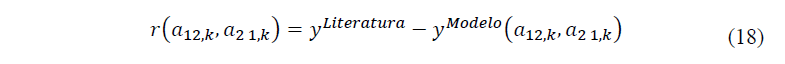
Logo, o método pode ser escrito como equação 18, que contém as atualizações dos parâmetros.
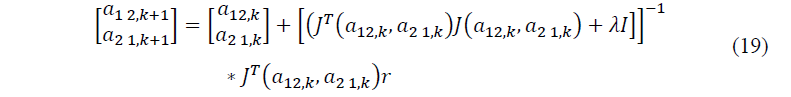

Por fim, o procedimento iterativo é interrompido quando o critério de parada é satisfeito, sendo baseado em um número máximo de atualizações dos parâmetros, ou seja, usado como ponto de interrupção a quantidade de 3 ∗ 104 de iterações.
3.3.2 Declive Máximo
O método do Declive máximo é uma técnica de otimização iterativo para encontrar o mínimo de uma função objetivo. Sendo útil em problemas que envolvem alta dimensionalidade e não lineares. O método baseia-se no fato de que o gradiente da função indica a direção de maior crescimento de f, logo, ao mover-se no sentido oposto ao gradiente, percorre-se a direção de maior declínio da função. Desta forma, a equação representa a função minimizada.
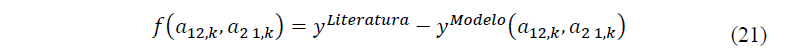
Dada a função objetivo, o método para atualização dos parâmetros na direção oposta ao gradiente, que aponta para a maior taxa de aumento da função, logo a atualização dos parâmetros é apresentada na equação 22.
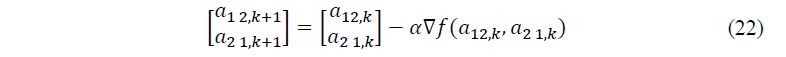
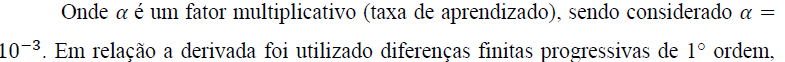

3.3.3 Newton-Raphson

Então o método pode ser escrito através da equação 24, onde a hessiana (h) que é a matriz das derivadas segundas, que fornece informação sobre a curvatura da função, para ajuste do tamanho e orientação do passo.
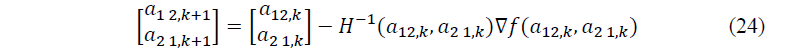

Em relação a derivada, foi utilizado diferenças finitas progressivas de 1° ordem, equação 20.
Para a Hessiana, que contém a segunda derivada, foram utilizadas diferenças finitas centrais de segunda ordem, sendo a equação 26 para derivada segunda parcial e a equação 27 para a derivada cruzada.

Por fim, como método de parada para o método é baseado na quantidade de atualização realizada, sendo até 3 ∗ 104.
3.4 Algoritmo genético
O algoritmo genético (AG) são métodos de busca estocástica inspirados nos processos de evolução natural das espécies, como a seleção natural e a reprodução sexuada. Neste modelo há uma flexibilidade com capacidade de geração para soluções eficazes para diversos problemas complexos e extensos (SCOLA, 2014).
Como o algoritmo genético é baseado em processos naturais, ocorre a combinação entre a sobrevivência do mais apto entre estruturas com uma troca de informação de forma aleatória, a cada geração, um novo conjunto de indivíduos é criado a partir dos mais aptos da geração passada (GOLDBERG, 1989).
A ordem para o algoritmo genético de forma genérica ocorre em 5 etapas
1° Geração da população inicial.
2° Avaliação a partir da aptidão para cada indivíduo.
3° Selecionar os indivíduos mais aptos.
4° Aplicação dos conceitos de crossover e mutação.
5° Verificação da condição de parada, caso a condição não seja atingida, retorna-se à 2° etapa, iniciando uma nova geração.
Neste trabalho, o (AG) foi utilizado para estimar os parâmetros binários do modelo UNIQUAC por meio da minimização do erro médio relativo (EMR) entre os valores calculados e os experimentais, a função objetivo é adotada é definido como a equação 28.

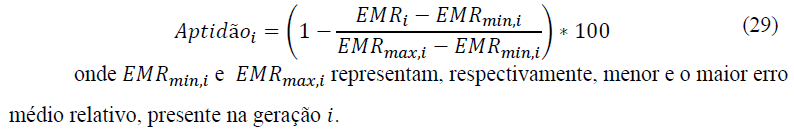
Os parâmetros de interação binária do modelo UNIQUAC foram representados por cromossomos em formato binário, com valores inicializados de forma aleatória dentro das faixas pré-definidas. O operador de seleção foi o método da roleta como forma de retenção dos melhores indivíduos. A operação de cruzamento adotado foi por meio de corte único, no qual os dois pais selecionados trocam partes dos seus cromossomos binários a partir de um ponto do cromossomo. A mutação binária aplicada que consiste na inversão aleatória dos genes.
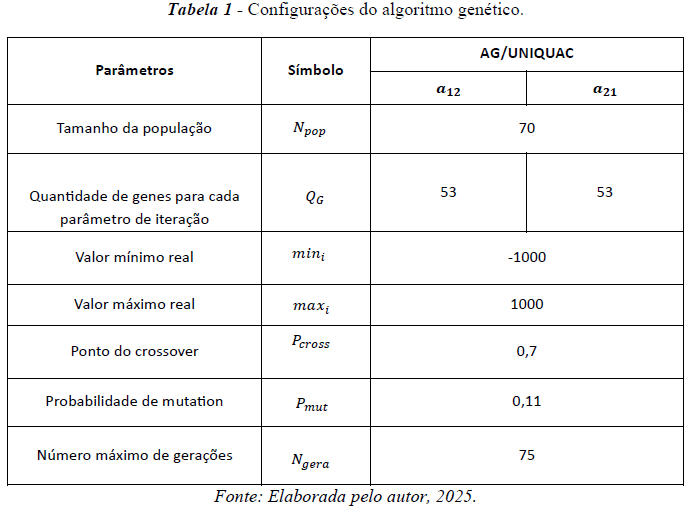
Por fim, as configurações do algoritmo, como tamanho da população, ponto de cruzamento, probabilidade de mutação e o critério de parada estão apresentados na Tabela 1. A partir do critério de parada, os indivíduos mais aptos de cada geração são avaliados por meio do Erro Médio Relativo (EMR), calculado conforme a equação (28). O indivíduo que apresentar o menor valor de EMR é considerado a melhor solução encontrada pelo algoritmo.
3.5 Critério de avaliação do ajuste
Para avaliar a representatividade promovida pelos ajustes entre os dados experimentais e os valores calculados pelos modelos, utilizou-se o erro médio relativo (EMR), sendo definido através da equação 28. Sendo apresentado os gráficos de erro relativo provocados pelos modelos, sendo essa a equação 30:
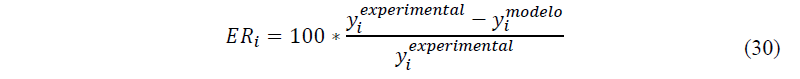
3.6 Implementação computacional
Todos os métodos utilizados neste trabalho :Levenberg-Marquardt, Declive máximo, Newton-Raphson e o Algoritmo Genético, foram implementados no ambiente MATLAB R2024a, e os gráficos foram construídos utilizando o software livre LabPlot e toda a implementação foi realizada em um computador pessoal Lenovo (R)Core(TM) i510300H CPU @ 2.50GHz 2.50 GHz.
4 RESULTADOS E DISCUSSÕES
Nesta seção, são apresentados os resultados obtidos a partir da aplicação dos métodos de predição de parâmetros do modelo termodinâmico UNIQUAC:
Levenberg-Marquardt, Máximo declive, Newton-Raphson e algoritmo genético. Os métodos foram utilizados para estimar os parâmetros de interação binária (aij) em sistemas binários, com base em dados experimentais.
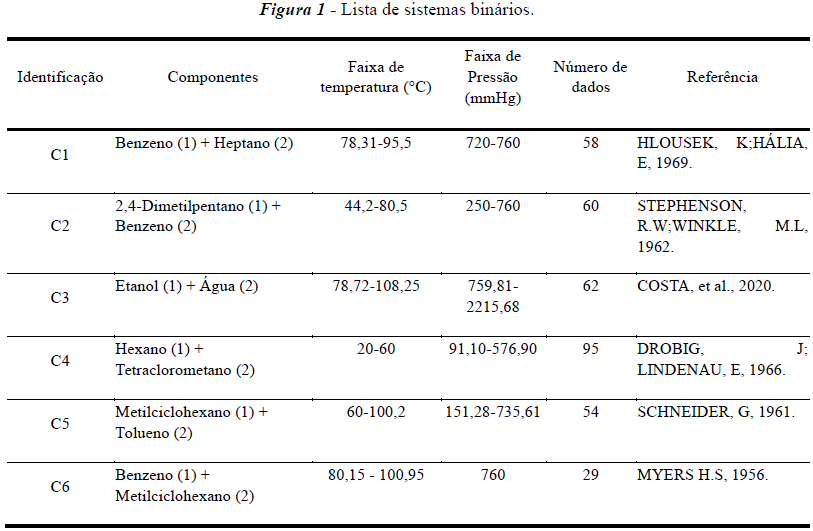
Com relação a seleção de dados experimentais de equilíbrio líquido-vapor, como mencionado na metodologia, foram obtidos através da coleção Vapor-Liquid Equilibrium Data Collection organizada por Gmehling et al., 1980-1983, logo, a partir disto, a Tabela 2 contém os seis sistemas binários escolhidos, as referências, faixa de temperatura, a faixa de pressão e a quantidade de dados presentes no experimento.
Ao longo deste trabalho, todos os dados experimentais, a partir da seleção dos seis sistemas binários, como constantes da equação de Antoine (psat), parâmetros de componente puro, como volume der Waals (r) e área de superfície (q), e os parâmetros de componente puro para determinação do coeficiente de fugacidade foram obtidos da literatura, sendo todos esses parâmetros dispostos no Apêndice B.
Para a consistência na aplicação da metodologia envolvendo os métodos determinísticos e o estocástico, pontos experimentais x1 = 0 e x1 = 1, foram retirados para estimação dos parâmetros binários, isto ocorre devido a um erro presente nos cálculos dos y′s, pois ocorre divisão utilizando xi, logo, este valor não pode ser nulo.
Nos métodos determinísticos, o denominado chute inicial, referente ao primeiro valor para os parâmetros de interação binária, sendo a12 = 0 e a21 = 0, desta forma, a Tabela 3 apresenta os resultados obtidos com a utilização dos métodos apresentados, onde está contido os sistemas, os parâmetros interação binária e o erro médio relativo apresentado pelos modelos previstos, tendo em vista que todos modelos obtiveram convergência para todos os sistemas escolhidos.
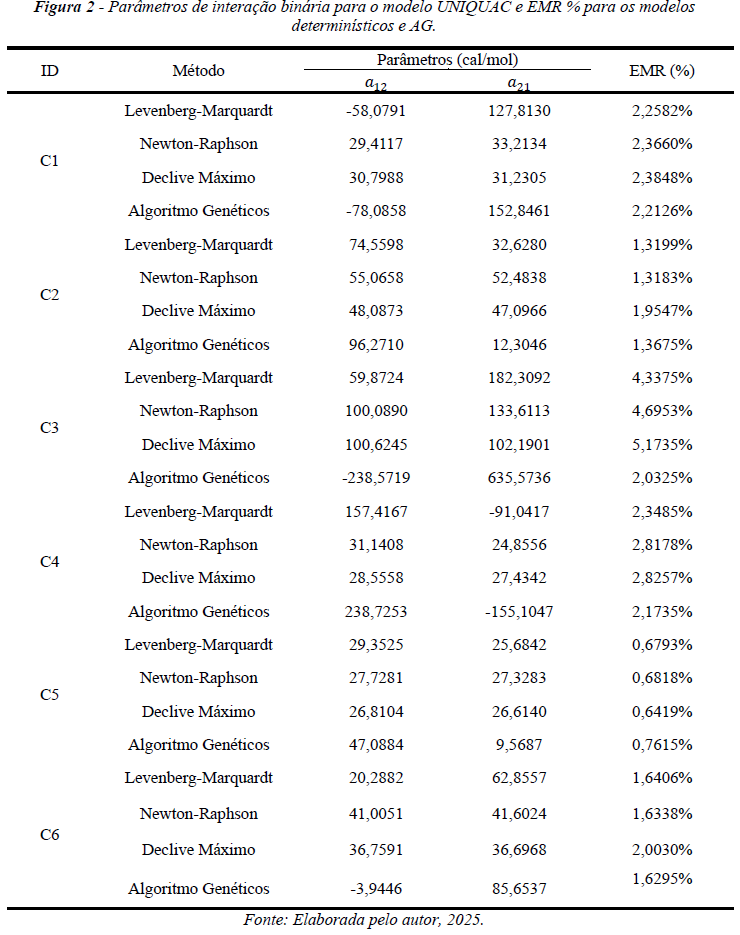
Observando os valores de EMR (%) apresentado na Tabela 2, é possível perceber que o algoritmo genético (AG) apresentou em 4 dos seis casos, os menores valores para erro médio relativo, sendo os sistemas C2 (2,4-Dimetilpentano (1) + Benzeno (2)) e o C5 (Metilciclohexano (1) + Tolueno (2)) que diferem. Desta forma, é evidenciado a sua capacidade de ajuste aos dados experimentais quando comparados aos métodos determinísticos tradicionais.
Com relação aos resultados do AG, no sistema C3, o algoritmo genético obteve um EMR (%) de 2,0325, enquanto o método Levenberg-Marquardt apresentou 4,3375, ou seja, sendo o dobro do modelo previsto pela AG, desta forma, a Figura 1 representa o erro relativo ao decorrer dos dados experimentais para cada modelo no sistema C3.
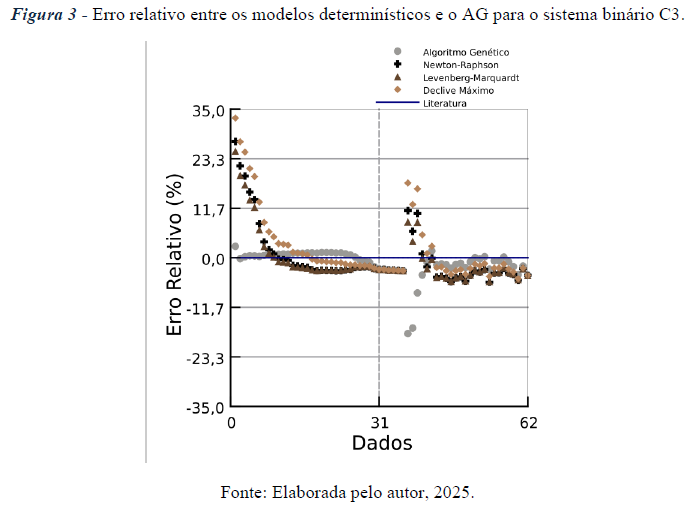
Através da Figura 1, para o sistema C3, onde o AG demonstrou maior representatividade quando comparado aos outros modelos, pode-se observar que modelos determinísticos possui um grande erro relativo nos dados iniciais, desta forma, provocando maiores valores para EMR (%), de acordo com os dados para o sistema, os modelos matemáticos possuem dificuldade com relação às baixas composições de x1. Diferentemente dos modelos determinísticos, o erro relativo do algoritmo genético é disposto próximo ao zero (literatura), e com variações acima de 10% para todos os modelos em partes dos dados previstos.
Apesar dos casos (C2 e C5) em que AG dispõem de EMR (%) que não sejam os menores, ainda assim o AG apresenta valores próximos dos que foram apresentados pelos modelos matemáticos, sendo aceitável sua utilização em ambas as situações. Com relação ao sistema C5, a Figura 2 apresenta o erro relativo (%) presente para cada dado experimental previsto pelos modelos.
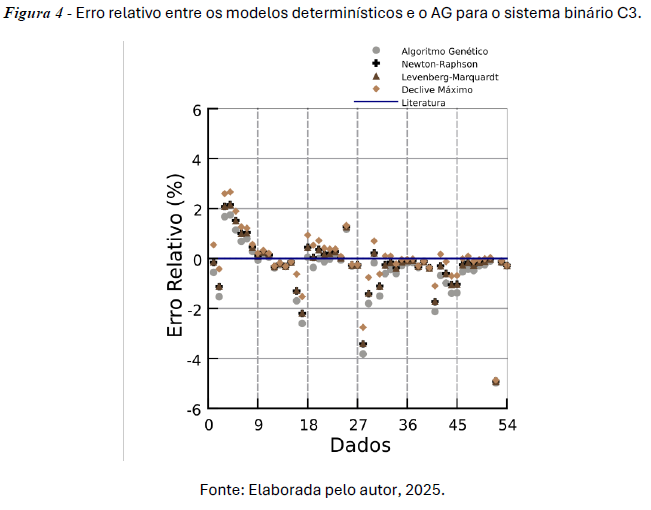
A Figura 2 apresenta o erro relativo (%) para o sistema C5, sendo que os dados presentes estão bem distribuídos diante dos dados da literatura, pode-se observar que o maior erro relativo está abaixo de -6%, neste sistema, todos os modelos possuem EMR (%) menor que 0,8 %, sendo o sistema com melhor representação através dos modelos apresentados.
Diante dos métodos determinísticos, o modelo de Levenberg-Marquardt obteve maior representatividade nos sistemas apresentados, tendo os menores EMR (%), como no sistema C2 (1,3199%). Logo, sua utilização com relação aos outros modelos apresenta um desempenho maior.
Os métodos de Newton-Raphson e Declive máximo apresentaram desempenhos próximos em C1, C4 e C5, isto é evidenciado diante dos parâmetros binários que foram previstos pelos modelos, onde em todos os sistemas, estes parâmetros são próximos, diferentemente dos que foram previstos pelo AG e pelo modelo Levenberg-Marquardt. O método de Declive máximo, mostrou-se mais sensível à escolha das estimativas iniciais e apresentou maiores erros nos sistemas C1, C2, C3, C4 e C6.
A partir dos resultados apresentados, o algoritmo genético obteve maior desempenho diante dos modelos determinísticos nos sistemas binários escolhidos, tendo destaque devido a menor variação do erro médio relativo ao decorrer dos diferentes sistemas. Desta forma, é evidente a robustez frente à natureza não linear do problema e sua capacidade de contornar mínimos locais, isto quando comparados aos métodos determinísticos. Diante dos modelos matemáticos, o modelo de Levenber-Marquardt apresentou resultados melhores diante dos sistemas avaliados, enquanto o método de Declive máximo apresentou sensibilidade em relação ao chute inicial.
5 CONCLUSÃO
Neste Trabalho, foi realizado a predição do equilíbrio líquido-vapor (ELV) por meio a estimativa dos parâmetros de interação binária do modelo termodinâmico Universal Quasi-Chemical (UNIQUAC), utilizando quatro abordagens distintas: Newton-Raphson, Levenberg-Marquardt, Declive máximo e algoritmo genético. Dados experimentais de sistemas binários disponíveis na literatura foram utilizados para a predição para comparação entre os modelos. Os resultados demonstraram que os métodos determinísticos apresentados são eficientes, diante das condições impostas, no entanto, apresentaram maior sensibilidade devido à escolha dos parâmetros iniciais, como observado nos modelos Newton-Raphson e Declive máximo.
Em relação ao algoritmo genético, foi observado maior desempenho, mesmo sem a necessidade de aproximações iniciais precisas e de derivadas. Nos sistemas escolhidos, o AG obteve na maioria dos casos analisados um menor erro médio relativo. Estas características tornam o método promissor para a modelagem de sistemas complexos, onde os problemas possuem natureza não linear.
Portanto, a comparação entre os métodos evidencia que a aplicação de técnicas de otimização estocásticas, como o algoritmo genético, pode contribuir significativamente para a melhoria na predição de dados termodinâmicos, complementado os métodos tradicionais.
Como perspectiva para trabalhos futuros relacionados ao equilíbrio líquido vapor, sugere-se a utilização de algoritmo genético como ferramenta para a definição de estimativas iniciais nos métodos determinísticos, com objetivo de contornar a sensibilidade desses métodos com a escolha dos parâmetros iniciais. Além disso, propõe-se a ampliação do uso de AG para sistemas multicomponentes, no contexto do modelo UNIQUAC, os quais envolvem um número maior de parâmetros de interação a serem ajustados.
REFERENCIAS
AZEVEDO, E. G; ALVES, A.M. ENGENHARIA DE PROCESSOS DE SEPARAÇÃO. 3.ed. Lisboa: IST Press, 2017.
CHERIC. Physical Properties of Tetrachloromethane. Disponível em: https://www.cheric.org/research/kdb/hcprop/showprop.php?cmpid=44. Acesso em: 22 set. 2024.
COSTA, T. K. O et al. Vapor-liquid equilibrium for binary systems ethanol (1) and water (2) and methyl acetate (1) and ethanol (2): Thermodynamic consistency and data prediction. Braz. J. of Develop., Curitiba, v. 6, n.6, p.36073-36093, jun.2020. Disponível: https://doi.org/10.34117/bjdv6n6-233. Acesso em: 10 out. 2023.
DROBIG, J.; LINDENAU, E. A new apparatus to determine the isothermal liquid-vapor equilibrium. Wissenschaftliche Zeitschrift der Technischen Hochschule für Chemie “Carl Schorlemmer” Leuna-Merseburg, v. 8, p. 144-147, 1966.
ERODOTOU, P; VOUTSAS, E; SARIMVEIS, H.A genetic algorithm approach for parameter estimation in vapour-liquid thermodynamic modelling problems. Computers & Chemical Engineering, v. 134, p. 106663, 2020. Disponível em: https://doi.org/10.1016/j.compchemeng.2019.106663. Acesso em: 06 Nov. 2024.
GMEHLING, J; ONKEN, U; ARLT, W. VAPOR-LIQUID EQUILIBRIUM DATA COLLECTION: Aliphatic Hydrocarbons C7-C18. Vol. I, Part 6b. Frankfurt: DECHEMA, 1980.
GMEHLING, J; ONKEN, U; ARLT, W. VAPOR-LIQUID EQUILIBRIUM DATA COLLECTION: Aliphatic Hydrocarbons C4-C6. Vol.I, Part 6A. Frankfurt: DECHEMA, 1980.
GMEHLING, J; ONKEN, U; KOLBE, B. VAPOR-LIQUID EQUILIBRIUM DATA COLLECTION: Aliphatic Hydrocarbons (Supplement 1). Vol.I, Part 6c. Frankfurt: DECHEMA, 1983.
GMEHLING, J et al. Chemical Thermodynamics for Process Simulation. 2.ed. Weinheim: Wiley-VCH, 2019. GOLDBERG, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning. 13.ed. Addison-Wesley:Michigan, 1989.
HLOUSEK, K; HÁLA, E. LIQUID-VAPOUR-EQUILIBRIUM. XLIII. The system benzene n-heptane at 720, 740, and 760 mmHg. Collect. Czech. Chem. Commun, Czechoslovak, v.35, n.4, p. (1030-1040), Julho, 1969. Disponível em: https://doi.org/10.1135/cccc19701030. Acesso em: 20 Set.2024.
MATSOUKAS, T. Fundamentals Of Chemical Engineering Thermodynamics: With Applications to Chemical Processes. 1.ed. Alemanha: Pearson, 2012.
MOREIRA, A. M. S; SACRAMENTO, M. de A; BUFFONI, S. S. de O. Métodos numéricos em programação não-linear sem restrição para minimização da energia potencial de uma treliça estrutural. In: SIMPÓSIO BRASILEIRO DE PESQUISA OPERACIONAL (SBPO), 39., 2007, Fortaleza. Anais… Fortaleza: Sociedade Brasileira de Pesquisa Operacional, 2007. Disponível em: http://ws2.din.uem.br/~ademir/sbpo/sbpo2007/trabalho/idx00.htm. Acesso em: 1 Mai. 2025.
MYERS, H. S. Binary mixtures of naphthenes and aromatics. Industrial & Engineering Chemistry, v. 48, n. 6, p. 1104–1108, 1956. Disponível em: https://doi.org/10.1021/ie50558a041. Acesso em: 9 maio 2025.
OLIVEIRA, H. N. M. Determinação de dados de Equilíbrio Líquido-Vapor para Sistemas Hidrocarbonetos e Desenvolvimento de uma nova Célula Dinâmica. 2003. Tese (Doutorado em Engenharia Química) – Universidade Federal do Rio Grande do Norte, Natal, 2003. Disponível em: https://repositorio.ufrn.br/handle/123456789/15939. Acesso em: 23 out. 2023.
PRAUSNITZ, J.M; LICHTENTHALER, R.N; AZEVEDO, E.D. MOLECULAR THERMODYNAMICS OF FLUID-PHASE EQUILIBRIA. 3.ed. New Jersey:Prentice Hall,1999.
SCHNEIDER, G. Zeitschrift für Physikalische Chemie (Frankfurt), v. 27, p. 171, 1961.
SILVA, J. J. .; MELLO, D. M. de .; PIRES, R. F.; DANTAS, S. C. Thermodynamic study of liquid-liquid equilibrium for the ethyl acetate + acetic acid + water system. Research, Society and Development, [S. l.], v. 11, n. 7, p. e9311729685, 2022. DOI: 10.33448/rsdv11i7.29685. Disponível em: https://rsdjournal.org/index.php/rsd/article/view/29685. Acesso em: 20 Set.2024.
STEPHENSON, R.W; WINKLE, M.L. Modification of Relative Volatilities by Addition of Solvent. Journal of Chemical and Engineering Data, Texas, v.7, n.4, p. (510-516), Outubro, 1962.Disponível em: https://doi.org/10.1021/je60015a021, Acesso em: 20 Set.2024.
SMITH, J.M et al. Introduction to Chemical Engineering Thermodynamics. 8.ed. New York: McGra-Hill, 2020.
APÊNDICE A – Equações auxiliares do coeficiente de fugacidade
Neste apêndice será apresentado as equações auxiliares utilizadas para determinação do coeficiente de fugacidade.
A partir disso, as equações A.1 e A.2, são as funções auxiliares.


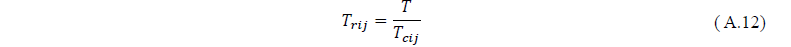

APÊNDICE B – Propriedades dos compostos
Neste apêndice serão apresentadas as propriedades para os compostos utilizados neste trabalho.
A Tabela B1, apresenta os parâmetros da equação de Antoine na forma.

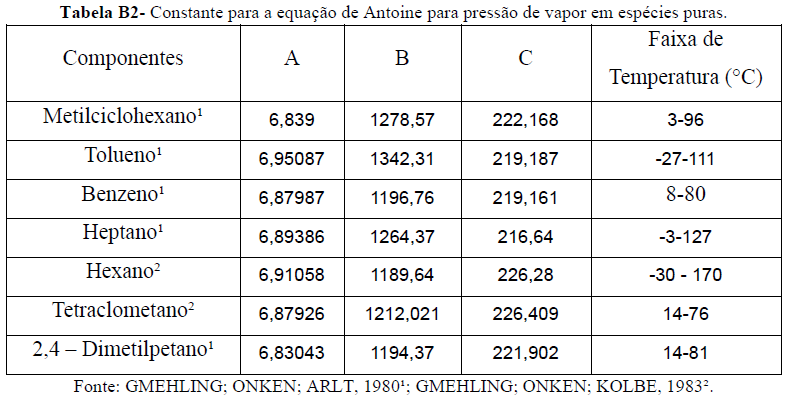
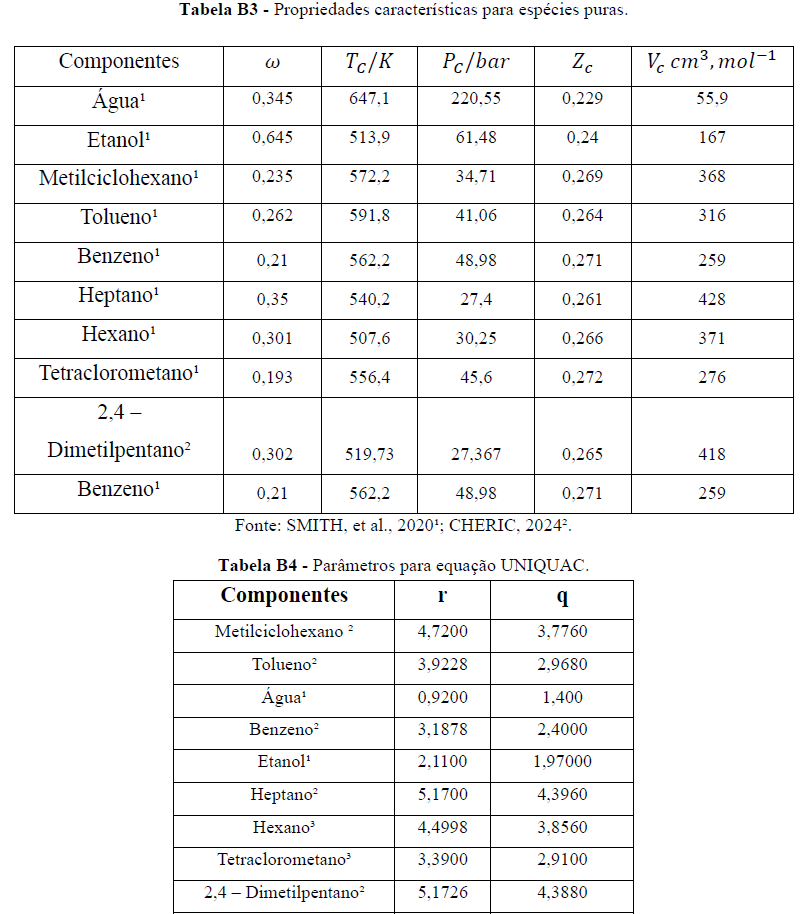
GMEHLING; ONKEN; KOLBE, 1983³;
1Discente do Curso Superior de Engenharia Química da Universidade Federal de Mato Grosso Campus Várzea Grande e-mail: samuelramos635@hotmail.com
