SAC, PRICE and MYTHS
REGISTRO DOI: 10.69849/revistaft/pa10202501191610
Ciro Pylro Gouvea1
Resumo
O presente artigo tem como propósito discutir a equivalência dos sistemas de amortizações mais adotados no Brasil: SAC e PRICE. Dentro da abordagem é apresentada a visão parcial que implica na sensação de não igualdade entre os dois modos quando analisados apenas os valores pagos ao longo da série histórica de quitação de um saldo devedor sem considerar o valor das parcelas atualizada pelas taxas e juros. Para fins demonstrações são apresentados exemplos e planilhas que apontam a equivalência dos fluxos de caixa em cada um dos modais de financiamentos e por fim uma demonstração geral, que comprova que um mesmo valor principal se mantém igual desse o ato da contratação do financiamento assim como no último período de pagamentos, quando os valores de cada uma das parcelas, tanto no SAC quanto no PRICE, são levados para o valor futuro líquido, gerando a igualdade das situações das dívidas.
Palavras-chave: Amortizações. SAC. PRICE. Equivalência. Juros.
Abstract
This article aims to discuss the equivalence of the most widely adopted amortization systems in Brazil: SAC and PRICE. Within the approach, a partial view is presented that implies the feeling of non- equality between the two methods when analyzing only the amounts paid throughout the historical series of settlement of a debt balance without considering the value of the installments updated by rates and interest. For demonstration purposes, examples and spreadsheets are presented that indicate the equivalence of cash flows in each of the financing methods and, finally, a general demonstration, which proves that the same principal value remains the same since the act of contracting the financing as well as in the last payment period, when the values of each of the installments, both in SAC and PRICE, are taken to the net future value, generating equality of the debt situations.
Keywords: Amortization. SAC. PRICE. Equivalence. Interest.
1 INTRODUÇÃO
A matemática financeira é uma ferramenta poderosa para a educação e formação do cidadão. É pelo bom uso desta habilidade que podemos gerar orçamentos familiares, condições necessárias e suficientes para que um bom investimento possa ser feito, aquisição ou mesmo contratação de uma dívida, etc.. No contexto de uma vida é comum observar em diferentes momentos a necessidade de analisar e refletir sobre a viabilidade de um endividamento. Para Assaf [1, p.13] a matemática financeira é o “estudo do dinheiro no tempo, ao longo do tempo”. Assim, as condições analíticas para estudos de viabilidades são temporais, sendo necessário o cuidado especial com o prazo da aplicação assim como se cuida da análise das taxas contratadas. Em consonância, propõem Zentgraf [2, p.2], “além de estudar os aspectos temporais do dinheiro, tais estudos objetivam estabelecer relações entre quantias monetárias expressas em datas diferentes”.
A literatura sobre matemática financeira é vasta. No contexto da educação básica brasileira estes assuntos em tese são trabalhados e constituem parte do currículo do Ensino Médio, conforme pode ser observado nas diretrizes da Base Nacional Comum Curricular (BNCC).
(EM13MAT203) Aplicar conceitos matemáticos no planejamento, na execução e na análise de ações envolvendo a utilização de aplicativos e a criação de planilhas (para o controle de orçamento familiar, simuladores de cálculos de juros simples e compostos, entre outros), para tomar decisões.
(EM13MAT303) Interpretar e comparar situações que envolvam juros simples com as que envolvem juros compostos, por meio de representações gráficas ou análise de planilhas, destacando o crescimento linear ou exponencial de cada caso.
Há tempos o assunto relacionado a finanças vem tomando proporções e relevância dentro da educação básica. Mas é preciso cuidado, em especial nos ativos financeiros miraculosos que desafiam a lógica do mercado. Potencializados pela publicidade cativante sobre o sucessos de influenciadores no universo dos produtos voltados para investidores, com relatos de incríveis de trajetórias em esquemas e carteiras que teoricamente rendem fortunas e em parco tempo aplicado. E é justamente neste contexto que muitos mitos são gerados, nas discussões com que apresentam argumentos retirados de fontes não confiáveis ou mesmo com cálculos imprecisos baseados em observações parciais.
Mas o desafio da educação financeira não se encerra quando se compreende que os juros compostos geram montantes maiores do que os juros simples em prazos longos. Também não se encerra quando é mostrado que existem diferentes formas de conceder descontos sobre um título de vencimento futuro. Ainda tem um espaço grande a ser percorrido, como análise de viabilidade, sistemas de amortização e capacidade de analisar de forma ampla cenários que podem ser vislumbrados com escolhas distintas de modais de pagamentos. Afinal de contas, é verdade que SAC é mais vantajoso para o credor de uma dívida do que o modelo PRICE? O mito da resposta “sim, SAC é melhor” é gerado quando a análise é parcial e não considera a temporalidade do pagamento de cada parcela corrigida ao longo da série até uma data comum de análise. O problema e origem do mito é que mesmo em vasta literatura sobre o tema, quase não se encontra uma boa discussão ou demonstração das equivalências dos dois modos de amortização, com publicações apegadas às aplicações dos sistemas e exercícios práticos como simulações, etc.. Desta forma, a demonstração das equivalências é uma contribuição ao tema e diminuição por consequência dos mitos sobre distinção entre os modos de financiamentos.
2 SAC e PRICE
Os financiamentos mais comuns no Brasil são o SAC (Sistema de Amortização Constante) e o PRICE (Sistema Francês de Amortização). Ambos relacionam uma série de pagamentos ao longo do tempo como forma parcelada de quitação de um saldo.
Assaf Neto propõem que sistemas de amortização são na verdade “operações de empréstimos e financiamentos de longo prazo, envolvendo desembolsos periódicos do principal e encargos financeiro” (2012, p. 205). Tais encargos são os juros, que representam uma manutenção do saldo devedor, sendo assim, justo pagar de forma proporcional ao que se deve no momento.
Já Milone (2006, p. 223) explica de forma acessível que:
“amortizar significa liquidar uma dívida mediante pagamentos periódicos sucessivos. Nas rendas certas, os pagamentos periódicos destinam-se a saldar compromissos; nelas cada pagamento comporta uma parcela do principal e uma dos juros devidos em função de uma taxa previamente combinada entre as partes” (2006, p. 223).
Os sistemas de amortização, de forma geral, representam pagamentos sucessivos e periódicos, com parcelas que são compostas de juros e de uma parte do saldo devedor (amortização). A soma das amortizações ao longo do período equivale ao valor principal, ou seja, a composição de cada parcela é dada pelo pagamento de uma fração da dívida contraída além de uma manutenção do saldo devedor na forma de juros proporcionais à situação da dívida.
2.1 SAC
A forma como é liquidado um saldo devedor quitando uma série de pagamentos periódicos, que liquidam parte a parte uma fração da dívida acrescidos de juros na forma de manutenção ou serviços de créditos. Neste modo, a amortização é uma constante e os juros são proporcionais ao saldo devedor, observa-se assim uma série de pagamentos como uma Progressão Aritmética decrescente.
Exemplo 1: Calcular a série de pagamentos de um financiamento via SAC de um crédito de R$ 35.000,00 com taxa de 10% ao mês em 10 meses consecutivos e com o primeiro pagamento 1 mês após a concessão do crédito.

Considere ainda que o mês 1 o saldo devedor é exatamente o valor principal da dívida.
A tabela 1 mostra os valores mês a mês da série de pagamentos:
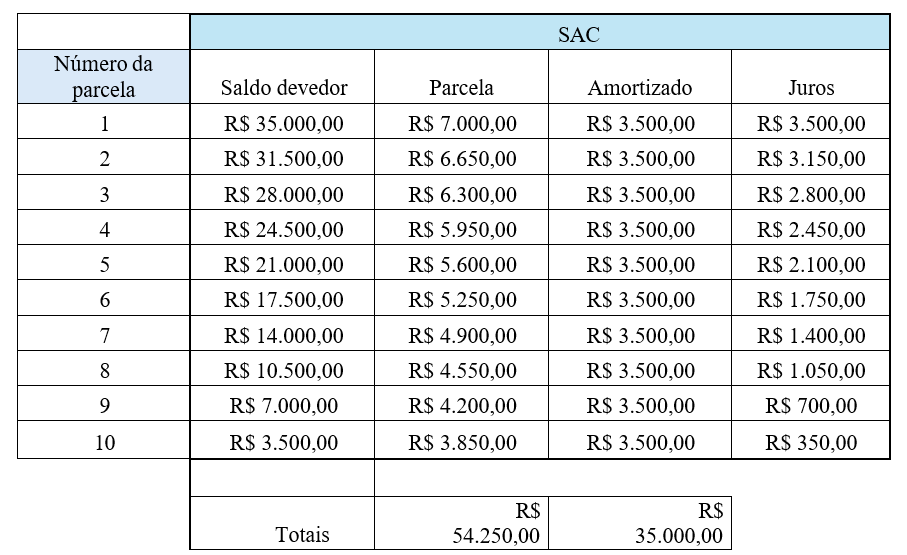
De modo geral, num financiamento de um valor principal Vp, com taxa i em n meses, observamos que cada parcela Pk pode ser encontrada usando a seguinte fórmula:

Como as parcelas consecutivas quitam uma parte constante da dívida, a amortização, então os juros proporcionais ao saldo devedor também caem de forma constante. Logo, tanto as parcelas, quanto saldo devedor e juros são elementos de uma Progressão Aritmética de razão conhecida.
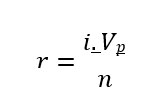
2.2 PRICE
O sistema de amortização PRICE é caracterizado por suas prestações constantes ao longo da série de pagamentos. Cada uma das parcelas é composta pela soma do valor amortizado com os juros, estes ainda proporcionais ao saldo devedor em cada momento.
Com a constância das parcelas consecutivas, o que muda em sua composição são os fatores de amortizações e juros, que ao longo do período compensam-se mutuamente pois a medida em que os valores dos juros caem em função da diminuição do saldo devedor, os valores amortizados ao longo do tempo sobem, compensando um ao outro e mantendo as parcelas constantes, característica própria do sistema francês de amortização.
Assim, um valor principal Vp contraído no sistema PRICE de pagamentos será liquidado em parcelas constantes
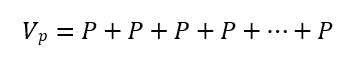
Trazendo para o valor presente cada uma das parcelas, concedendo os descontos compostos por dentro, é possível calcular qual é o valor do desembolso P constante em cada período:
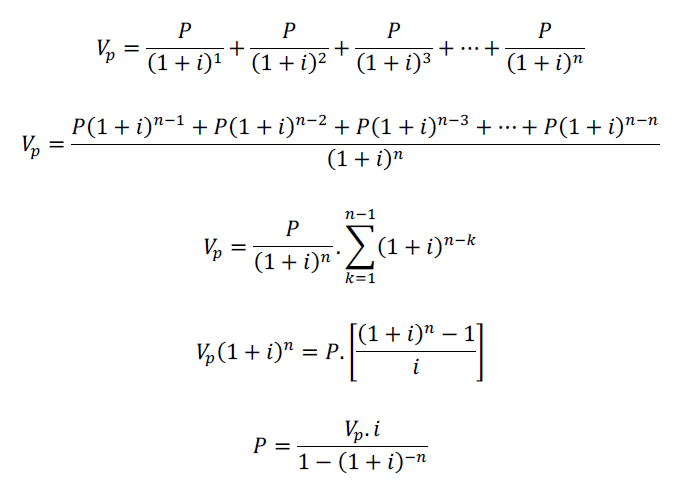
Exemplo 2: Calcular a série de pagamentos de um financiamento com sistema de amortização PRICE de um crédito de R$ 35.000,00 com taxa de 10% ao mês em 10 meses consecutivos e com o primeiro pagamento 1 mês após a concessão do crédito.
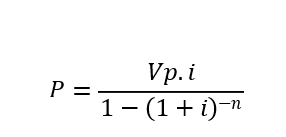
Onde P é o valor da parcela, Vp é o valor principal (crédito concedido), i é a taxa mensal
e n o número de períodos.
Logo,
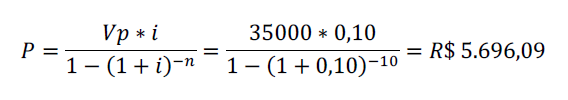
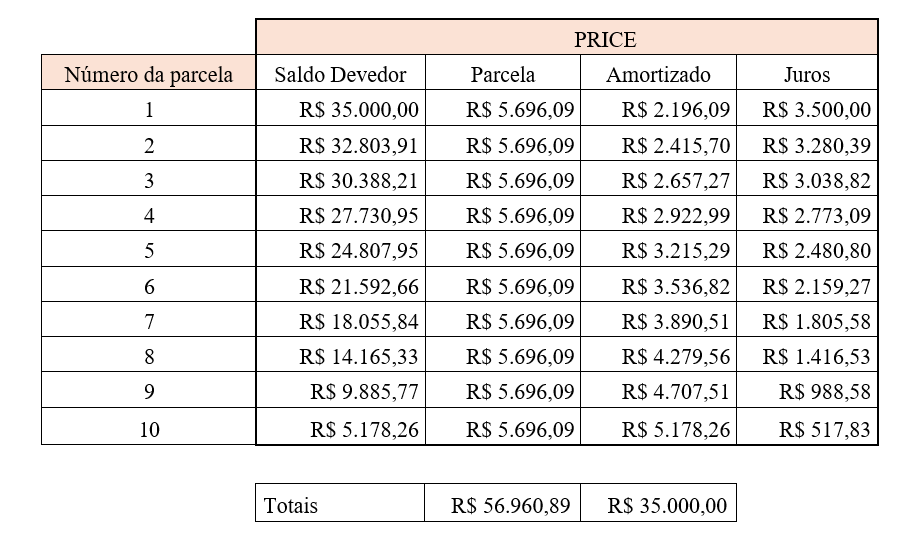
A tabela 2 mostra os valores mês a mês da série de pagamentos:
3 As condições para formação do Mito
Conforme observado, as parcelas no PRICE são contantes, enquanto no SAC são decrescentes e obedecem aos termos de uma progressão aritmética. Mas o mito que surge: qual dos dois modais de pagamentos é mais ou menos interessante para o tomador do empréstimo? É comum analisarem os dados destas duas tabelas das séries de pagamentos e concluir que o SAC tem a soma nominal das parcelas inferior que a soma nominal das parcelas em PRICE, ou ainda, que em cada período, os juros em cada parcela PRICE é maior ou igual aos juros em cada parcela SAC no mesmo período, conforme observado no gráfico 01, gerado pelas comparações dos juros das tabela 1 e 2:
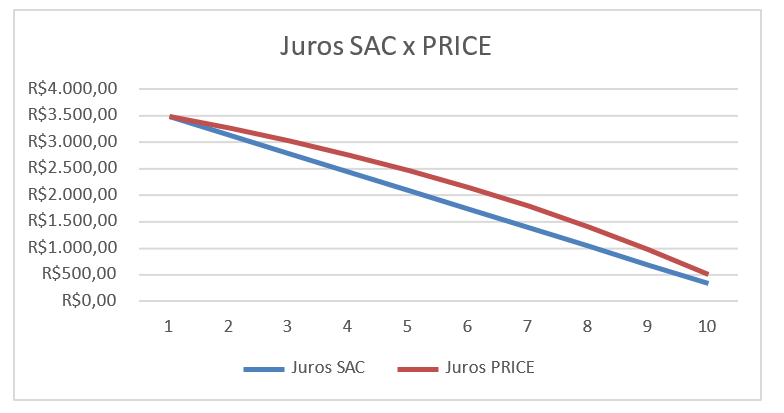
De fato há clara diferença entre os valores mês a mês entre os dois modais, mas implicar na melhor opção apenas por estes fatores não é justo uma vez que as diferenças de valores de parcelas podem ser aplicadas em investimentos numa mesma taxa equivalente ao proposto no próprio financiamento. Se há uma equivalência entre os dois modos de financiamento então a diferença entre as parcelas pode ser aplicada num investimento de tal modo que os períodos superavitários geram caixa para suprir os meses deficitários.
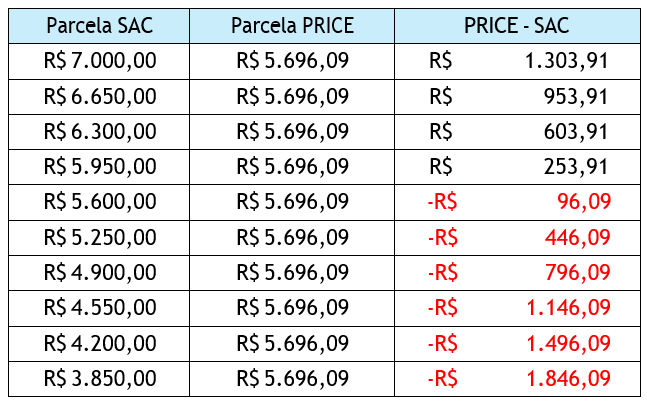
A tabela 3 mostra a diferença observada nos valores das parcelas pagas com os modais SAC e o PRICE indicadas em tabela 1 e tabela 2:
3.1 Refutando o mito
Como é de se esperar, as parcelas SAC no início do financiamento são maiores que as parcelas PRICE e por isso há um saldo gerado por esta diferença. Já nos últimos pagamentos a situação é invertida, tornando menos oneroso mensalmente o pagamento SAC em relação ao PRICE, deixando assim um saldo negativo nos meses subsequentes.
Tomando a diferença entre os valores das parcelas do SAC e PRICE e realizando um investimento de tal modo que o fluxo de caixa obedece a necessidade de depósito ou retirada para compensação, e aplicando ainda a mesma taxa de 10% contratadas nos exemplos 1 e 2 obtém-se o montante mensal apresentado na tabela 4:
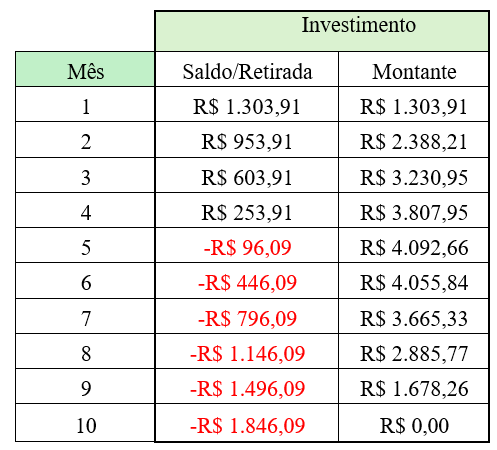
Para composição do montante foi considerado o aporte mensal advindo da diferença entre os valores das parcelas SAC e PRICE acrescido dos juros de 10% ao mês do saldo já acumulado. Inicialmente o montante gerado na aplicação apresenta superávits corrigidos e acumulados. Já na segunda metade do financiamento os aportes viram retiradas, compensando o valor das parcelas do SAC menores que as parcelas do PRICE.
O que é observado, no último período, é o montante igual a R$ 0,00, implicando na constatação, para estes exemplos propostos, de que ambos os sistemas de amortização são equivalentes quando a diferença é investida para gerar caixa para os períodos deficitários, uma vez que o investimento não produziu montante residual ou dívidas restantes após o pagamento de todas as parcelas.
3.1 Uma prova geral da equivalência SAC e PRICE e liquidando o mito

3.1.1 Postergando para o período n todas as parcelas do PRICE
Assim como em 2.2 cada parcela em PRICE pode ser calculada fazendo:
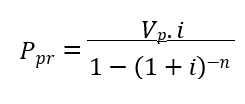
Ao postergar cada uma das n parcelas de valor P para o período n gera o Valor Futuro Líquido do PRICE (VFLpr), aplicando as correções de juros compostos:
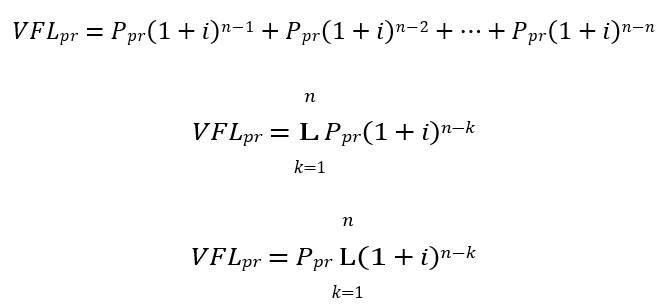
Mas a expressão contida no somatório é uma soma de uma progressão geométrica.
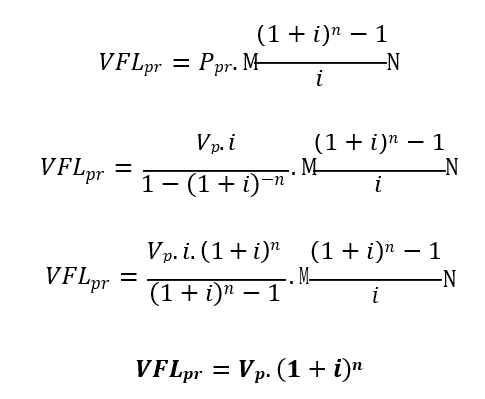
Portanto, conclui-se que cada uma das parcelas Ppr contratadas no sistema de pagamentos, quando levadas para o período n da série gera o valor Vp atualizado em juros compostos com n períodos e taxa i ao período. Isso comprova que o sistema PRICE é justo sobre a concessão e quitação dos débitos.
3.1.2 Postergando para o período n todas as parcelas do SAC
Assim como em 2.1, cada parcela do sistema de pagamento em SAC pode ser calculada fazendo:
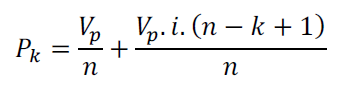
Logo, postergar cada uma destas parcelas para o período n gera o Valor Futuro Líquido
SAC (VFLs/):
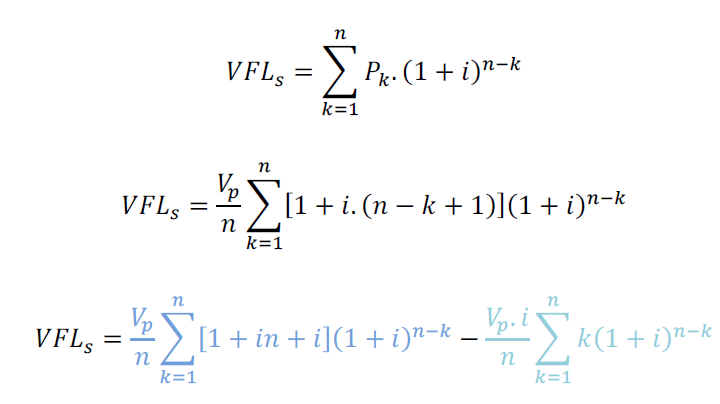
Para simplificar a compreensão das parcelas em somatórios vamos separar em duas
etapas, sendo a primeira um somatório que se resume na soma de uma Progressão Geométrica
e a segunda que será mais bem trabalhada, sendo transformada numa soma de séries de
Progressões Geométricas.
(i) Calculando o primeiro somatório, uma progressão geométrica:
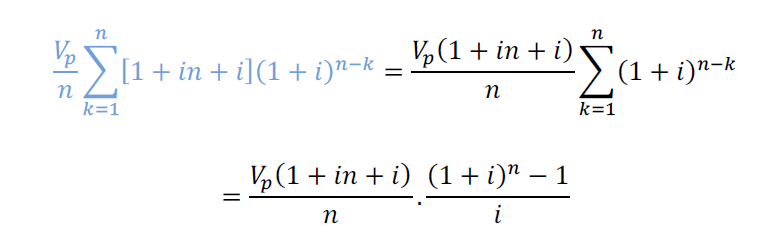
(ii) Expandindo e remodelando o segundo somatório:
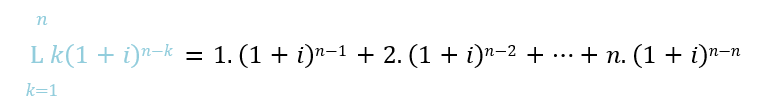
Ao abrir o somatório e reorganizando a distribuição e ocorrência de cada uma das parcelas, é possível notar que aparece uma estrutura de soma na qual organização aparenta ser mais simples quando disposto na forma de um “triângulo de somas”:
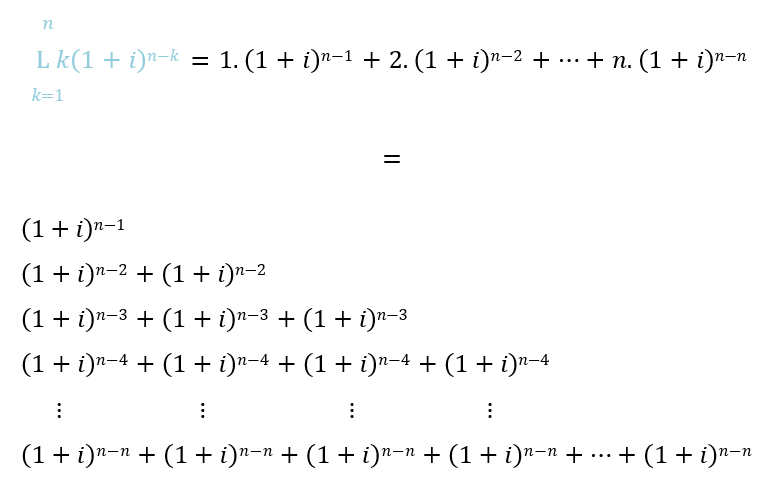
Cada uma das n colunas é verticalmente uma soma de uma progressão geométrica, cujo primeiro termo é o primeiro elemento da coluna e a razão (1 + i).
Assim, a soma de cada colunas Ci do “triângulo de somas” é apresentada abaixo:
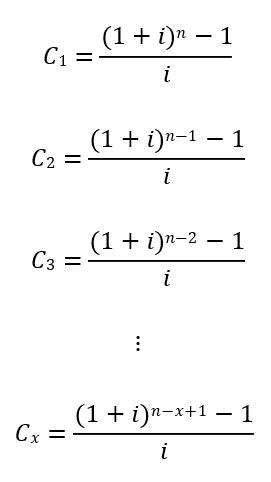
Assim, o somatório (ii) pode ser redesenhado e reescrito como uma soma de PG de razão (1 + i).


Ou seja, demonstramos que no período n:
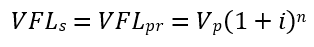
4 RESULTADOS E DISCUSSÕES OU ANÁLISE DOS DADOS
Diante da pergunta sobre o que é mais vantajoso entre SAC e PRICE, os exemplos aplicados são pedagógicos e excelentes para uma introdução ao tema das amortizações. Se o processo de educação encerra suas discussões neste ponto, abre-se uma lacuna na plena compreensão do tema pois a discussão temporal é fundamental para compreender que é mito diferenciar os modos sem propor investimentos que acabam mostrando de forma justa suas equivalências.
A discussão sobre justiça ou não entre as formas de pagamentos de financiamentos via SAC ou PRICE é parca quando analisados apenas os valores nominais pagos ao longo da série. É certo analisar o perfil do crédito dentro das capacidades financeiras daquele que o toma, pois as diferenças entre os modais não são condições que balizam propostas de ganhos ou perdas, mas as condições temporais de aportes variáveis ou constantes são sim fatores decisivos para uma boa escolha.
O mito sobre qual dos dois modos (SAC ou PRICE) é melhor é definitivamente desvendado quando é proposta a análise do custo do dinheiro ao longo do tempo.
Ainda sobre a demonstração geral das equivalências, literaturas sobre matemática financeira podem e devem apropriar-se de ferramentas, incentivadas desde a educação básica até o ensino técnico e superior, para confrontar, balizar ou confirmar com mais propriedades as escolhas financeiras pelas condições corretas.
5 CONSIDERAÇÕES FINAIS
Este artigo, por meio de demonstrações gerais e estudo de casos prova e demonstra a tese de que SAC e PRICE são equivalentes quando temos por hipótese as condições iniciais iguais em valores, prazo e taxas. Indica ainda que é equivocado pensar na não equivalência quando analisadas distantes da temporalidade os valores nominais de cada parcela.
O processo de compreensão da matemática financeira passa pela análise temporal do valor do dinheiro e, não distante desta condição, o mito é encerrado ao promover de forma justa a equivalência do valor futuro líquido das duas séries para o último período.
Para futuros estudos a respeito do tema é interessante propor alternativas de financiamentos, e de forma análoga demonstrar que também são equivalentes quando se valem das mesmas condições de taxas e tempo e sujeitos a juros proporcionais ao saldo devedor em cada período. Sistemas como Americano e o SAM (sistema de amortização misto) estão entre eles e certamente geram mais condições para novas propostas e análises.
REFERÊNCIAS
ASSAF Neto, A. Finanças Corporativas e Valor. 2a ed. São Paulo: Atlas, 2005.
ZENTGRAF, R. O Guia Prático de Finanças do Roberto Zentgraf: aprenda a lidar com seu dinheiro de forma inteligente. Rio de Janeiro: Elsevier, 2009.
. Base Nacional Comum Curricular. https://www.gov.br/mec/pt-br/escola-em-tempo- integral/BNCC_EI_EF_110518_versaofinal.pdf . Acessado em 10 de janeiro de 2025.
. Lei de Diretrizes e Bases da Educação Nacional Nº. 9394, de 20 de dezembro de 1996. Disponível em: http://www.planalto.gov.br/ccivil_03/leis/l9394.htm. Acesso em: 10 de janeiro de 2025.
1 Discente do Curso de mestrado profissional em Matemática, PROFMAT da Universidade Federal do Espírito Santo (UFES) Campus Goiabeiras
e-mail: maildociro@gmail.com
