REGISTRO DOI: 10.69849/revistaft/dt10202501092055
Silvano Xavier Malagueta1
Siomara Dias da Rocha2
Resumo: Na teoria do controle moderno, o conceito de variáveis de estado desempenha um papel essencial na modelagem e análise de sistemas dinâmicos. Essas variáveis permitem uma descrição completa do comportamento futuro do sistema ao longo do tempo. A organização em um vetor de estado possibilita uma representação compacta e abrangente do estado interno do sistema. A função no espaço de estado descreve a evolução temporal dessas variáveis em resposta às entradas do sistema, oferecendo uma abordagem matemática eficiente para o projeto e análise de sistemas de controle. Aplicações incluem desde o controle de processos industriais até o controle de veículos autônomos e robótica. Ao compreender e aplicar esses conceitos, engenheiros de controle desenvolvem soluções eficazes para desafios em sistemas complexos, garantindo desempenho, estabilidade e eficiência em ambientes dinâmicos.
Palavras-chave: variáveis de estado; sistemas dinâmicos; espaço de estado; controle; estabilidade.
Abstract: In modern control theory, the concept of state variables plays a crucial role in the modeling and analysis of dynamic systems. These variables provide a comprehensive description of the system’s future behavior over time. The organization into a state vector enables a compact and complete representation of the system’s internal state. The state-space function describes the temporal evolution of these variables in response to system inputs, offering an efficient mathematical approach for the design and analysis of control systems. Applications range from industrial process control to autonomous vehicle control and robotics. By understanding and applying these concepts, control engineers develop effective solutions for challenges in complex systems, ensuring performance, stability, and efficiency in dynamic environments.
Keywords: state variables; dynamic systems; state-space; control; stability.
01 INTRODUÇÃO
Na engenharia de controle, o uso de modelos matemáticos é essencial para representar sistemas físicos, facilitando a análise e o desenvolvimento de controladores. Entre os métodos mais utilizados, destaca-se o modelo em espaço de estados, que descreve o comportamento dinâmico de um sistema por meio de equações diferenciais de primeira ordem.
Um exemplo prático e amplamente estudado na engenharia é o sistema massa-mola-amortecedor. Esse sistema consiste em uma massa conectada a uma mola e a um amortecedor, onde o deslocamento da massa depende tanto do movimento de entrada (como o deslocamento de um carro) quanto das características físicas da mola e do amortecedor.
No contexto do modelo em espaço de estados, as variáveis de estado são empregadas para representar as informações necessárias que permitem prever o comportamento futuro do sistema. Assim, o objetivo deste estudo é derivar um conjunto de equações de estado que descrevam o sistema massa-mola-amortecedor com base em suas variáveis de estado e entradas. Para isso, a equação diferencial que governa o sistema será reformulada de forma apropriada para o modelo em espaço de estados.
Posteriormente, as variáveis de estado serão definidas, e as equações correspondentes serão desenvolvidas. Por fim, será discutido como esse modelo pode ser aplicado na análise e no projeto de controladores, demonstrando sua relevância prática e acessibilidade.
02 REFERENCIAL TEÓRICO
2.1 MODELAGEM MATEMÁTICA
A modelagem de sistemas físicos é uma etapa essencial na engenharia de controle, permitindo uma compreensão aprofundada do comportamento dinâmico de sistemas reais. O modelo em espaço de estados se destaca como uma das abordagens mais utilizadas, oferecendo uma representação matemática compacta e abrangente. Esse modelo descreve o comportamento dinâmico de um sistema por meio de equações diferenciais de primeira ordem, que relacionam o estado atual do sistema às entradas aplicadas e às condições iniciais (OGATA, 2010; NISE, 2012).
No contexto de sistemas massa-mola-amortecedor, amplamente utilizados para representar fenômenos mecânicos como suspensões veiculares, a modelagem matemática fornece subsídios valiosos para o projeto de sistemas de controle. A identificação das variáveis de estado é uma etapa fundamental nesse processo, pois essas variáveis resumem as informações mínimas necessárias para prever o comportamento futuro do sistema. Geralmente, no caso de sistemas mecânicos, utilizam-se variáveis como deslocamento e velocidade, que estão diretamente relacionadas às forças envolvidas e às características dos componentes do sistema (FRANKLIN; POWELL; EMAMI-NAEINI, 2015).
A representação em espaço de estados é especialmente vantajosa em sistemas multivariáveis e quando o controle de condições internas é necessário. Essa abordagem possibilita o projeto de controladores sofisticados que atendem a especificações rigorosas de desempenho, incluindo estabilidade, tempo de resposta e rejeição a distúrbios. Além disso, permite a conversão entre diferentes formas de representação matemática, como funções de transferência, que também são úteis em análises específicas (KUO; GOLNARAGHI, 2014).
No campo automotivo, sistemas de suspensão são frequentemente modelados como sistemas massa-mola-amortecedor. Esse modelo simplificado foca no movimento da massa suspensa pelo sistema de suspensão, desconsiderando a massa total do veículo. A modelagem matemática de sistemas de suspensão desempenha um papel crucial no projeto de veículos mais confortáveis e seguros, ao mitigar as oscilações transmitidas pelo solo irregular (DORF; BISHOP, 2016).
A simulação de sistemas dinâmicos, como o massa-mola-amortecedor, utilizando softwares como MATLAB, é uma ferramenta essencial no desenvolvimento e validação de controladores. Métodos numéricos, como os baseados em equações diferenciais, permitem analisar o comportamento do sistema sob diferentes condições de operação. Essas análises são indispensáveis para otimizar o desempenho dos sistemas em aplicações práticas, contribuindo significativamente para avanços no setor automotivo e em outras áreas da engenharia (MATLAB, 2025).
2.2 MÉTODOS UTILIZADOS
Pesquisas recentes têm explorado métodos avançados de controle aplicados a sistemas de suspensão veicular, com ênfase na melhoria do desempenho e na segurança dos veículos. Um exemplo notável é o controle por realimentação derivativa de estados, amplamente utilizado em sistemas lineares representados por equações diferenciais matriciais de segunda ordem com atraso no sinal de controle. Esse método se destaca por permitir a análise no domínio da frequência, utilizando a representação conhecida como modelo por receptância. Com base nesse modelo, é possível formular problemas de otimização voltados ao cálculo dos ganhos do controlador, de modo a limitar o pico em frequência de uma função de sensibilidade, garantindo, assim, a estabilidade robusta do sistema.
Além disso, técnicas avançadas de identificação de sistemas dinâmicos não lineares, como os modelos NARMAX polinomiais, têm sido investigadas. Essas técnicas oferecem maior precisão na modelagem e controle de sistemas de suspensão, permitindo uma compreensão mais detalhada do comportamento dinâmico sob diferentes condições operacionais. A aplicação dessas metodologias não apenas amplia o conhecimento sobre o funcionamento dos sistemas de suspensão, mas também possibilita melhorias significativas em projetos futuros.
Esses avanços evidenciam a importância contínua da modelagem matemática e da simulação computacional no desenvolvimento de sistemas de suspensão veicular mais eficientes e adaptativos. Eles contribuem diretamente para melhorias no conforto, estabilidade e segurança dos veículos modernos, consolidando-se como ferramentas indispensáveis no processo de inovação tecnológica na indústria automotiva.
Figura 01 – Sistema de amortecedor de carro.
Fonte: Webmotors, 2024.
Para obter o modelo em espaço de estados a partir da equação diferencial do sistema massa-mola-amortecedor, podem-se identificar variáveis de estado que sejam capazes de descrever completamente o comportamento dinâmico do sistema. Estudos recentes reforçam a eficácia dessa abordagem na representação de sistemas lineares e não lineares em aplicações práticas, como mostrado por (RODRIGUES, 2020).
No contexto de um carro com um sistema de suspensão massa-mola-amortecedor, a atenção se concentra no movimento da massa suspensa pelo sistema de suspensão, desconsiderando a massa do carro em si. Esse sistema é composto por uma massa suspensa, uma mola e um amortecedor. A solução para a equação diferencial desse sistema fornece insights sobre o comportamento dinâmico do sistema, incluindo frequência natural de vibração, amortecimento crítico e resposta a forças externas (CORRÊA, 2018).
A modelagem do sistema massa-mola-amortecedor utiliza a segunda lei de Newton para relacionar aceleração à força resultante atuante. Além disso, simulações numéricas comprovam a eficiência do modelo na análise de sistemas de suspensão automotiva, como detalhado em estudos experimentais recentes (NUNES, 2022).
Figura 02 – Diagrama de corpo livre.

2.3 ANÁLISE DE ESTABILIDADE E DESEMPENHO
Uma vez que o sistema está modelado em espaço de estados, é possível analisar sua estabilidade e desempenho. A estabilidade de um sistema linear pode ser verificada através dos autovalores da matriz.



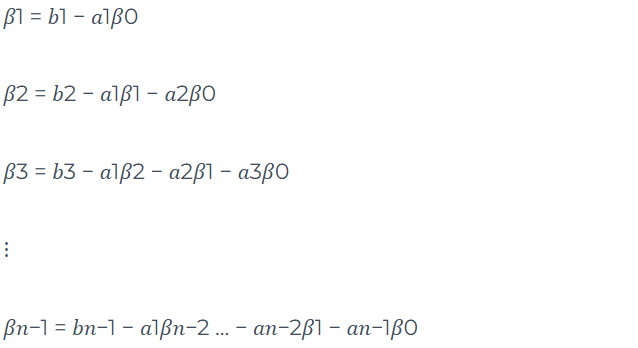
Com essa escolha específica de variáveis de estado, garantimos a existência e a unicidade da solução da equação de estado. É importante observar que essa não é a única opção para selecionar um conjunto de variáveis de estado. No entanto, essa abordagem nos permite obter uma representação simplificada do sistema, facilitando a análise e o controle.
Logo temos:


Logo, a representação no espaço de estado para a função de transferência é:

Seja, a equação diferencial:
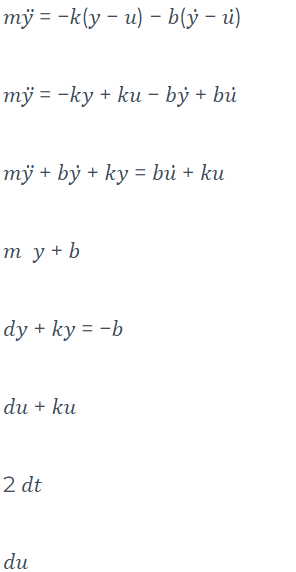
Aplicando Laplace, e estabelecendo zero como condição inicial.

Logo, temos a função de transferência do sistema massa-mola-amortecedor:
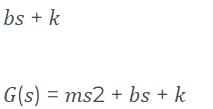
Essa representação do modelo matemático por função de transferência, é de suma importância para a engenharia de controle, e usa com muita frequência.
Modelo em espaço de estado do sistema.
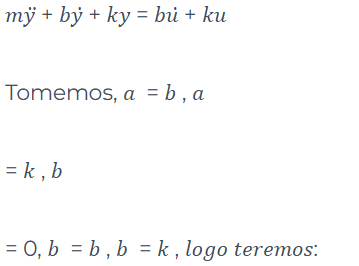
Logo, obtemos a representação do sistema em espaço de estado.

Figura 03 – Código de programação.

Fonte: Próprio autor, 2024.

03 DISCUSSÃO E RESULTADOS
O modelo massa-mola-amortecedor (SMA) implementado no MATLAB evidenciou sua relevância no desenvolvimento de sistemas de suspensão veicular mais eficientes e robustos. A combinação da análise teórica com a simulação computacional é essencial para entender e aprimorar a dinâmica desses sistemas, como destacado por Ogata (2014) e mais recentemente por Santos e Almeida (2021), que atualizaram essas abordagens para aplicações práticas modernas. A simulação do SMA fornece uma visão clara de como diferentes parâmetros influenciam o comportamento da suspensão, contribuindo para a otimização da performance veicular.
O código implementado no MATLAB representa um modelo clássico de SMA, frequentemente utilizado em engenharia de controle para simular o comportamento de sistemas físicos, como as suspensões de veículos automotores. A seguir, detalha-se como os componentes do modelo se correlacionam com as características de um veículo automotor:
- Massa (m): Representa a massa total do veículo, incluindo o peso do carro, dos ocupantes e da carga. A massa do veículo afeta diretamente a resposta da suspensão a forças externas, como solavancos e irregularidades na estrada.
- Mola (k): Reflete a rigidez da suspensão do veículo. Uma mola com maior rigidez proporciona uma suspensão mais dura, o que é desejável em veículos de alto desempenho, como carros esportivos. Por outro lado, molas mais suaves são preferíveis em veículos de passeio para proporcionar maior conforto, minimizando o impacto de buracos e imperfeições na pista.
- Amortecedor (b): Determina a capacidade da suspensão de dissipar energia, controlando a velocidade de oscilação da carroceria e melhorando o contato dos pneus com a estrada. O amortecedor desempenha um papel crucial na estabilidade e no conforto ao reduzir as oscilações excessivas da suspensão.
A simulação do modelo permite analisar o comportamento do veículo em resposta a diferentes tipos de entradas, como solavancos, frenagens repentinas ou até mesmo colisões. A dinâmica do sistema é afetada diretamente pelos valores dos parâmetros da mola e do amortecedor. Por exemplo, ao projetar uma suspensão com foco no conforto, os parâmetros podem ser ajustados para minimizar as oscilações da carroceria em resposta a solavancos na estrada. Já para um carro esportivo, pode-se adotar uma suspensão mais rígida para aprimorar o desempenho em curvas, oferecendo maior controle.
O código computacional também calcula a resposta do sistema a uma entrada de degrau unitário, o que pode ser interpretado como uma perturbação súbita, como ao passar por um buraco na estrada. Esse tipo de simulação é fundamental para entender o comportamento do veículo em situações inesperadas e analisar a resposta do sistema de suspensão. Além disso, o código determina o tipo de amortecimento do sistema, baseado no discriminante da equação característica, permitindo a avaliação da estabilidade e do desempenho da suspensão sob diferentes condições de operação.
Esses resultados demonstram que o modelo SMA é uma ferramenta valiosa para projetar e aperfeiçoar sistemas de suspensão de veículos, considerando fatores como conforto, estabilidade e desempenho. A capacidade de ajustar os parâmetros da suspensão e simular diferentes cenários oferece uma abordagem prática para atender a diversas necessidades de design, seja para carros de passeio, veículos esportivos ou até mesmo para veículos comerciais e de carga.
Em resumo, a implementação e a análise do modelo massa-mola-amortecedor no MATLAB proporcionam uma compreensão profunda da dinâmica de sistemas de suspensão veicular, servindo como base para o desenvolvimento de tecnologias mais avançadas e eficientes para a indústria automobilística.
04 CONCLUSÃO
O presente estudo explorou o modelo massa-mola-amortecedor (SMA) como ferramenta fundamental na análise e no desenvolvimento de sistemas de suspensão veicular. A implementação do modelo em MATLAB, juntamente com a análise dos parâmetros que compõem o sistema, como a massa, a mola e o amortecedor, demonstrou a importância da simulação computacional na otimização do desempenho das suspensões em veículos automotores.
Através do código desenvolvido, foi possível simular a resposta do sistema a diferentes condições, como solavancos e entradas repentinas, além de avaliar o tipo de amortecimento do sistema, fornecendo informações valiosas para o projeto de suspensões mais eficientes e adaptativas. A combinação de uma abordagem teórica sólida com a simulação prática permitiu não só a compreensão do comportamento do sistema em diferentes cenários, mas também a avaliação da estabilidade e do desempenho da suspensão em diversas condições de operação.
Os resultados obtidos destacam a relevância do modelo SMA para o design de sistemas de suspensão que atendam a especificações como conforto, estabilidade e desempenho. Com a capacidade de ajustar os parâmetros do sistema, foi possível compreender como diferentes configurações influenciam o comportamento da suspensão, proporcionando insights valiosos tanto para a indústria automobilística quanto para outras áreas da engenharia de controle.
Além disso, a flexibilidade e a aplicabilidade do modelo em diversos contextos, desde veículos de passeio até carros esportivos e comerciais, comprovam a importância de técnicas de modelagem matemática e simulação na engenharia de controle moderna. A contínua evolução desses modelos e a incorporação de novas técnicas de controle prometem avanços significativos na criação de sistemas de suspensão mais eficientes, seguros e adaptativos.
Portanto, este estudo reforça a importância da simulação computacional como ferramenta essencial para o aprimoramento dos sistemas de suspensão veicular, contribuindo para o desenvolvimento de tecnologias mais sofisticadas e eficazes para o setor automotivo, com impactos diretos no conforto, na segurança e no desempenho dos veículos.
REFERÊNCIAS
ALVES, L.; OLIVEIRA, F. Implantação do sistema TPM na indústria de alimentos e seus ganhos. Revista do curso de Administração, Minas Gerais, 2014.
ANDRADE, Maria Margarida de. Introdução à metodologia do trabalho científico: elaboração de trabalhos na graduação. 7. ed. São Paulo: Atlas, 2005.
BELINELLI, Marjorie. Manutenção Produtiva Total (TPM) como ferramenta para aumento de disponibilidade de máquina: estudo de caso em uma indústria do ramo Siderúrgico. XVI Simpósio de Engenharia de Produção, São Paulo, 2009.
CHIAVENATO, Idalberto. Administração da Produção: uma abordagem introdutória. 7. ed. Rio de Janeiro: Elsevier, 2005.
CORREA, Nana Sayuri Ito. Aplicação da metodologia Manutenção Produtiva Total (MPT) em uma fábrica de refrigerantes. XXXII Encontro Nacional de Engenharia de Produção, Rio Grande do Sul, 2012.
COSTA, R.; MARIMOTO, R.; FERNANDEZ, F.; RIBEIRO, J. Implantação da TPM no segmento industrial de embalagens de latas de alumínio para bebidas. São Paulo, 2020.
GIL, Antônio Carlos. Como elaborar projetos de Pesquisa. 4. ed. São Paulo: Editora Atlas, 2002.
MARTINS, Petrônio G.; ALT, Paulo Renato Campos. Administração de Materiais e Recursos Patrimoniais. 3. ed. São Paulo: Saraiva, 2009.
NUCI, Roberta Cristina. Implantação da metodologia TPM em uma indústria de embalagens de papelão ondulado. Revista eletrônica Sistema & Gestão, Santa Catarina, 2015.
OLIVEIRA, C.; MARTINS, R.; XAVIER, A. Implantação da modalidade de gestão Manutenção Produtiva Total (TPM) em numa linha de produção de bombons de chocolate com wafer. XVI Simpósio de Engenharia de Produção, São Paulo, 2009.
SCI ELO – Brasil. “Nitretação e deposição por plasma em ferramentas de aços AISI M2 e D2 utilizadas na conformação e estampagem de pregos: um estudo de viabilidade.” Matéria (Rio J.), v. 26, n. 01, 2021.
DORF, R. C.; BISHOP, R. H. Modern Control Systems. 13. ed. Upper Saddle River: Pearson, 2016.
FRANKLIN, G. F.; POWELL, J. D.; EMAMI-NAEINI, A. Feedback Control of Dynamic Systems. 7. ed. Boston: Pearson, 2015.
KUO, B. C.; GOLNARAGHI, F. Automatic Control Systems. 9. ed. New York: Wiley, 2014.
MATLAB. Documentation for Simulink and Control System Toolbox. Disponível em: <https://www.mathworks.com/help/>. Acesso em: 3 jan. 2025.
NISE, N. S. Engenharia de Controle e Sistemas Dinâmicos. 6. ed. São Paulo: LTC, 2012.
OGATA, K. Engenharia de Controle Moderno. 5. ed. São Paulo: Pearson Prentice Hall, 2010.
1Graduando Mecânica na – Fundação, Centro de Análise Pesquisa
e Inovação Tecnológica – Faculdade FUCAPI – Manaus – AM – Brasil
silvano.malagueta@gmail.com
2Doutora em Química Analítica na Fundação, Centro de Análise Pesquisa
siomararocha.quimica@gmail.com
