MATEMÁTICA ACADÊMICA E MATEMÁTICA ESCOLAR NO ÂMBITO DO CURSO DE GRADUAÇÃO EM LICENCIATURA EM MATEMÁTICA

REGISTRO DOI: 10.69849/revistaft/ma10202412180922

Francisco Newton do Nascimento Santos
Orientador: Prof. Dr. José Nilton de Abreu Costa

Resumo

Neste artigo é feita uma análise da relação existente entre a Matemática Acadêmica e Matemática Escolar no âmbito do curso de graduação em licenciatura em matemática. São trazidas definições de ambas baseadas em autores que argumentam sobre o tema. Oportunamente, é ainda destacada a importância dessas concepções na formação dos professores de matemática e do matemático. Os autores pesquisados e seus escritos formam toda base teórica do trabalho, que consiste numa pesquisa bibliográfica, para que seja possível observar que, embora exista uma relação fundamental entre elas, também existe uma diferença perceptível. No curso de licenciatura em matemática, é possível verificar a existência de disciplinas que contemplam cada uma das duas perspectivas citadas. Em face disso, o presente trabalho tem como objetivo é estabelecer uma análise sobre as contribuições que a Matemática Acadêmica e a Matemática Escolar fornecem para a formação e atuação do professor, que facilitam a aprendizagem do aluno, com definições mais descritivas e uso de metodologias que visem comunicar o conhecimento matemático de uma forma objetiva e prática.

Palavras-chave: Formação de professores de Matemática, Matemática acadêmica, Matemática Escolar.

Abstract

This article analyzes the relationship between academic mathematics and school mathematics in the context of undergraduate mathematics courses. Definitions of both are provided, based on authors who argue on the subject. The importance of these conceptions in the training of mathematics teachers and mathematicians is also highlighted. The authors researched and their writings form the entire theoretical basis of the work, which consists of a bibliographical survey, so that it is possible to observe that, although there is a fundamental relationship between them, there is also a perceptible difference. In the mathematics degree course, it is possible to verify the existence of subjects that contemplate each of the two perspectives mentioned. In view of this, the aim of this paper is to establish an analysis of the contributions that Academic Mathematics and School Mathematics make to teacher training and performance, which facilitate student learning, with more descriptive definitions and the use of methodologies aimed at communicating mathematical knowledge in an objective and practical way.

Keywords: Mathematics teacher training, Academic mathematics, School mathematics.

1. Introdução

A Educação Matemática nos anos finais do Ensino Fundamental e no Ensino Médio, com Base na Base Nacional Comum Curricular e nas avaliações de larga escala como Sistema de Avaliação da Educação Básica (SAEB) e Exame Nacional do Ensino Médio (ENEM), exigem do professor de matemática um conhecimento amplo e diversificado, não só em nível acadêmico, mas também em nível escolar, quando se trata em comunicar o saber matemático para o aluno. Isso se deve a uma clara diferença que existe entre a Matemática Acadêmica e a Matemática Escolar, entre o Matemático e o Professor de Matemática, e essas diferenças, mesmo que sejam complementares, fazem com que muitos professores, ao sair do curso de licenciatura em matemática, tenham dificuldades em lidar com essas diferenças.

Fiorentini (2013) defende que o professor de matemática precisa conhecer, com profundidade e diversidade, a matemática enquanto prática social e que diz respeito não apenas ao campo científico, mas, sobretudo, à matemática escolar e às múltiplas matemáticas presentes, mobilizadas e produzidas nas mais diversas práticas cotidianas.

Este artigo faz uma reflexão sobre o desenvolvimento acadêmico e a prática escolar, de modo a não diminuir nenhuma das concepções ora denominadas Matemática Acadêmica e Matemática Escolar. Conforme Nascimento e Santos (2021), a ideia não é rivalizar e também não é atribuir “uma matemática” como sendo mais importante do que “a outra”. Ao contrário, o propósito é mostrar que nenhuma das “duas matemáticas” deve prevalecer diante da outra, pois assim seria criada uma hierarquia, tornando os componentes curriculares como peças separadas, gerando assim um problema, tendo em vista que ambas são necessárias à formação do professor.

Sobre esse binômio, de acordo com Moreira e David (2003), a Matemática Acadêmica é o corpo de conhecimentos construídos por matemáticos profissionais. Por outro lado, a Matemática Escolar é a apresentação dos resultados matemáticos, que são mostrados aos estudantes descartando a possibilidade de dúvidas, por conta da confiabilidade depositada na Matemática Acadêmica. Assim, esta última busca práticas metodológicas que procurem garantir ao estudante a compreensão dos conteúdos matemáticos essenciais.

É possível observar, ainda, a distinção que existe entre o Matemático e o Professor de Matemática. O primeiro agente participa ativamente na produção e consolidação do conhecimento matemático, enquanto o segundo recorre ao uso de metodologias e práticas para tornar acessível a aprendizagem dos alunos. Conforme Fiorentini e Lorenzato (2006) apud Felicetti (2010), há uma diferença entre os dois: o matemático direciona-se para a Matemática em si, estuda seus conteúdos formais, concebe a Matemática como um fim em si mesmo, enquanto que o professor/educador matemático a concebe como um meio, uma ferramenta à formação do educando, tentando promover uma educação pela Matemática. O objetivo deste artigo é analisar as contribuições que a Matemática Acadêmica e a Matemática Escolar fornecem para a formação e atuação do professor, facilitando a aprendizagem do aluno. Sabendo que existe uma relação de mútua cooperação e contribuição entre ambas, isso torna relevante a análise para que haja um bom desenvolvimento do professor e para que seu desempenho em sala de aula seja o mais eficaz possível. Observando que muitas vezes tal diferença não é percebida e nem estudada, e que ainda se faz algum tipo de confusão em relação à aplicação específica de cada abordagem citada, causou a motivação para a realização desta análise. Espera-se que, de alguma forma, este trabalho ajude na reflexão dos futuros alunos e futuros professores de matemática, para uma docência que busque executar de forma satisfatória a educação matemática.

2. Fundamentação Teórica

A construção desse artigo tomou como base obras de autores e pesquisadores no tema em pauta. Foi, ainda, consultada uma quantidade relevante de artigos que abordam a presente temática. Desse modo, tem-se uma revisão bibliográfica que fundamenta e norteia o presente manuscrito.

2.1 Formação de professores de Matemática

A formação do professor é o real objetivo de um curso de licenciatura em matemática. Então, refletir sobre mudanças que podem ocorrer nesse processo é de extrema relevância na busca de evoluir sempre na qualificação e formação do aluno do curso de licenciatura, que se tornará na maioria das vezes um professor de matemática e, ao se deparar com os desafios presentes na vida escolar, poderá contar com conhecimento acadêmico e pedagógico para transpor os desafios.

Há mais um século, o matemático alemão Felix Klein denunciava, em sua célebre obra Matemática Elementar de Um Ponto de Vista Superior (editada pela primeira vez em 1908), uma alienação entre a formação universitária de professores de matemática e a prática de sala de aula da escola básica. O autor identifica essa ruptura como uma dupla descontinuidade: por um lado, quando os estudantes ingressam nos cursos universitários de formação de professores, poucas relações são estabelecidas entre a matemática com que passam a ter contato e aquela anteriormente aprendida por eles como alunos da escola básica; e por outro lado, quando concluem esses cursos e iniciam a vida profissional, poucas relações são estabelecidas entre a matemática aprendida durante a graduação e aquela que passa a ser demandada pela prática de sala de aula da escola básica.

Assim, é como se, ao ingressar na universidade, o futuro professor devesse esquecer toda a matemática que aprendeu até então na escola básica; e ao terminar a graduação, o professor devesse novamente esquecer toda a matemática ali aprendida para se iniciar na carreira docente. Em consequência, o curso universitário pode ter um efeito essencialmente inócuo na formação do professor.

Pode-se perceber que a formação de professores exige, cada vez mais, que os cursos de licenciatura adotem um formato no qual as disciplinas, de forma geral, capacitem o professor para fazer uso tanto da Matemática Acadêmica quanto da Matemática Escolar. Nos programas de formação de professores são encontradas, frequentemente, disciplinas em que a Matemática Escolar (considerada elementar) é apresentada a partir de uma perspectiva acadêmica (avançada). Entre outros, podemos citar os seguintes exemplos: em disciplinas da área de Álgebra, o conjunto dos números inteiros e o conjunto dos polinômios são vistos, muitas vezes, como exemplos particulares de anéis euclidianos; áreas de algumas figuras geométricas podem ser calculadas a partir da noção de integral definida, etc. (MOREIRA; DAVID, 2011).

No Brasil, segundo o diagnóstico de Moreira (2012), ainda que o chamado modelo “3+1” (três anos de disciplinas de “conteúdo”, seguidos de um ano de disciplinas de “pedagogia”) tenha sido abandonado na maior parte dos cursos de licenciatura em matemática, seu princípio basilar permanece presente. Esses cursos continuam se estruturando por meio da justaposição de módulos sobre o “conteúdo matemático” e módulos sobre “pedagogia” que, apesar de em geral não serem mais separados em anos letivos diferentes, ainda são projetados e executados sem articulação.

E, como mostram Fiorentini et al. (2002) apud Nascimento e Santos (2021), os principais problemas da licenciatura em matemática, no geral, parecem ter mudado pouco nos últimos 25 anos. Foram constatadas as existências: de dicotomias entre teoria e prática e entre disciplinas específicas e pedagógicas; de distanciamento entre o que os futuros professores aprendem na licenciatura e o que realmente necessitam na prática escolar; de pouca articulação entre as disciplinas e os docentes do curso; de predominância de práticas de ensino e avaliação tradicionais, sobretudo por parte dos professores da área específica; de ausência de uma formação histórica, filosófica e epistemológica do saber matemático; de menor prestígio da licenciatura em relação ao bacharelado.

Logo, não resta dúvida que ponderar sobre esse tema tem grande relevância para o ensino de matemática. Isso pois, de acordo com os Parâmetros Curriculares Nacionais, Parte dos problemas referentes ao ensino de Matemática estão relacionados ao processo de formação do magistério, tanto em relação à formação inicial como à formação continuada. (BRASIL, 1997).

Pode-se exemplificar citando currículos adotados por cursos de licenciatura, nos quais se percebe uma significativa tendência para conteúdos direcionados à Matemática Acadêmica. Alguns currículos de cursos de licenciatura são concebidos tendo como referência principal os currículos dos cursos de bacharelado correspondentes, dos quais são excluídos os tópicos considerados “difíceis” ou “desnecessários” para o professor. Assim, a licenciatura é concebida como um bacharelado mutilado. Essa é uma perspectiva negativa para a formação de professores, pois se sustenta em premissas apenas sobre aquilo que o professor não precisa saber, sem levar em consideração os saberes necessários para a prática.

Destaca-se que, de modo algum, a Matemática Acadêmica perde sua importância ou espaço fundamental no processo de formação. Constitui, assim, uma parte fundamental do currículo de formação dos professores de matemática da educação básica. Embora outras partes sejam também consideradas importantes, elas são vistas essencialmente como instrumentos auxiliares para o professor no desenvolvimento do trabalho escolar de ensino da matemática (MOREIRA; DAVID, 2011).

Com isso, para desenvolver um trabalho equilibrado, o professor precisa ter a capacidade de realizar uma ligação entre as concepções acadêmica e escolar de comunicar o saber matemático. Ainda, segundo Moreira e David (2011), o resultado final é que, embora o conhecimento do conteúdo tenda a ocupar o centro de gravidade do processo de formação do professor, a matemática oferecida nesse processo é raramente submetida a uma análise crítica, tomando como base as necessidades da futura prática profissional. A possibilidade de integrar o conhecimento matemático acadêmico com o conhecimento matemático associado às demandas da prática docente escolar é tida como certa, ainda que não se tenha clareza sobre o significado concreto do termo integrar, nesse contexto.

Por fim, a tarefa de construir ligações substantivas entre o processo de formação e a prática profissional do professor é remetida para o exterior da formação matemática.

2.2 Matemático e o Professor de Matemática

É importante ressaltar que existe uma diferença entre o Matemático e o Professor de Matemática, sendo que a formação do segundo precisa ser diversificada, contendo conhecimentos específicos e do cotidiano para que auxiliem a prática da docência na Educação Matemática.

Realizar uma análise em relação ao processo de formação oferecido por cursos de licenciaturas em Matemática e o perfil dos professores ao final do curso, ganha grande relevância para obtenção do resultado esperado na vida profissional. Sabe-se que o professor no começo da docência poderá cometer erros e certamente encontrará dificuldades. Segundo Garcia (1999) apud Lima e Belmar (2016), o professor principiante pode ser acometido por quatro erros. Primeiro, uma repetição acrítica de condutas observadas nos pares; segundo, o isolamento dos seus colegas; terceiro, a dificuldade em efetuar a transposição didática dos conhecimentos adquiridos durante a formação inicial; quarto, assumir uma concepção técnica do ensino, pautando-se em uma educação exclusivamente bancária.

As dificuldades dos professores iniciantes incluem ainda a questão da diversidade de alunos encontrados em uma mesma sala de aula, diversidade essa que se reflete nas diferenças de ritmo de aprendizagem, nas diferenças de comportamento e de atitude frente às tarefas e atividades propostas pelo professor, etc. É claro que esse tipo de dificuldade, como todas as anteriormente mencionadas, é comum aos profissionais docentes, iniciantes ou não, mas elas costumam ser mais intensas nos anos iniciais de exercício da profissão (SANTANA, 2016).

O grande desafio do professor de matemática em relação ao Ensino e Educação Matemática é promover acesso ao conhecimento que tenha como consequência o questionamento previsível e imprevisível, que só acontece na sala de aula, orientar como desenvolver investigação sobre o conhecimento matemático, aplicando-o em seu cotidiano. Tornando assim o saber matemático relevante para a vida cotidiana e desfazendo qualquer ideia negativa que possa existir para o estudo da matemática.

O professor de Matemática, ou de qualquer outra área, tem que ser explorador do conhecimento e cada vez mais se renovar com novas metodologias de ensino, para acompanhar o raciocínio dos alunos em relação ao mundo, principalmente quando se trata da matemática, por ser classificada como difícil. Eis uma questão que a sociedade impõe sobre ela, a dificuldade. Isto ocorre por falta de elo da matemática com o mundo, o qual deveria começar a ser trabalhado na formação inicial dos professores, que através deste poderia facilitar a compreensão dos alunos em relação a esta área (MACEDO; LINS, 2014).

Desse modo, Lorenzato (2008) infere que o ensino da matemática, para ser proveitoso ao aluno, precisa estar vinculado à realidade na qual este está inserido. Para tanto, o ensino da matemática precisa ser planejado e ministrado tendo em vista o complexo contexto de identificação de seus alunos, considerando e respeitando a cultura deles, bem como suas inspirações, necessidades e possibilidades. Quanto aos desafios encontrados, Utsumi (2021) considera o seguinte: promover experiências matemáticas e o aprendizado dos conteúdos matemáticos escolares continua sendo um grande e constante desafio do professor que se propõe a atingir a função da matemática na vida escolar e extraescolar de seus alunos.

Pode-se compreender que, o processo de ensino e aprendizagem necessita de tempo, continuidade e recursos didáticos para que o professor desempenhe à docência de forma eficaz e para que os alunos participem ativamente nesse processo. Dar aulas é bem diferente de ensinar. Ensinar é dar condições para que o aluno construa seu próprio conhecimento. Vale salientar a concepção de que há ensino somente quando, em decorrência dele, houver aprendizagem (LORENZATO, 2008 apud SILVA, 2023).

Em face disso, pode-se concluir que as funções exercidas por ambos no campo profissional são distintas. A busca pela excelência no desempenho profissional passa pela clareza que se deve ter em relação à concepção que será aplicada. O fato é que o matemático e o professor de matemática da Educação Básica exercem duas profissões distintas e devem, portanto, construir, ao longo dos seus respectivos processos de formação, olhares profissionais distintos para a matemática relevante em cada um dos seus campos de atuação profissional. A matemática relevante para o matemático não é capaz de fornecer ao professor uma mirada profissional específica para a sala de aula da escola, do mesmo modo que a matemática relevante para a sala de aula da escola é incapaz de fornecer ao futuro matemático uma mirada profissional específica para o trabalho de produção de novos resultados na fronteira do conhecimento acadêmico (MOREIRA, 2012).

2.3 Matemática Escolar x Matemática Acadêmica

Será feita uma reflexão sobre como cada uma dessas concepções são definidas. Refletindo sobre as diferenças que existem entre as duas e a contribuição para comunicação do conhecimento matemático. Podemos citar a forma que ambas interpretam o erro. O erro, na matemática escolar, é muitas vezes entendido como um fenômeno psicológico que envolve aspectos diretamente relacionados com o desenvolvimento dos processos de ensino e aprendizagem e, por isso, positivos, já que podem indicar obstáculos cognitivos (importantes de serem diagnosticados) ou germens de conhecimentos novos. Na matemática acadêmica, o erro é negativo, um fenômeno lógico que expressa a contradição de algum fato estabelecido como verdadeiro (VILELA; MENEGHETTI, 2011).

Assim, não se tem como objetivo estabelecer um conflito entre às práticas, mas levar os professores a uma reflexão sobre o uso da matemática escolar, sem deixar de considerar a parte acadêmica que encontramos na Universidade. Segundo Moreira (2010) apud Nascimento e Santos (2021), Chevallard toma a Matemática Científica como a fonte privilegiada de saber à qual o sistema escolar sempre recorre para se recompatibilizar com a sociedade. E toma, também, esse saber científico como a referência última que permitiria à comunidade dos matemáticos desautorizar o objeto de ensino que não seja considerado “suficientemente próximo ao saber sábio”. Assim, a Matemática Escolar se constituiria essencialmente pela adaptação à escola dos conceitos, métodos e técnicas da Matemática Científica.

Fica evidenciada a ideia de que não há nem valorização e nem desvalorização em relação a nenhuma das concepções. Wasserman et al. (2019) defendem que a Matemática Acadêmica pode fornecer uma base para o ensino, pois fornece uma compreensão mais profunda e promove uma base rigorosa para as ideias da Matemática Escolar. Além disso, ela tem o papel de reforçar o envolvimento com conteúdos avançados, que auxiliem na compreensão da matemática como disciplina (WASSERMAN et al., 2019 apud JARDIM; RIBEIRO; AGUIAR, 2022).

De acordo com Moreira e David (2003), a Matemática acadêmica é o corpo de conhecimentos construídos por matemáticos profissionais. Com isso, as demonstrações, definições e provas de um fato e rigor na linguagem utilizada ocupam papel relevante, visto que é por meio deles que determinado conhecimento é aceito como verdadeiro pela comunidade científica.

Podemos citar alguns exemplos de afirmações matemáticas que são colocadas nos livros didáticos e não sofrem nenhum tipo de desconfiança por parte dos professores, mas que quando indagados pelos alunos acaba gerando dificuldades em responder pelo fato de depender de uma demonstração de nível acadêmico.

Vejamos:

Por que 1° é igual a 60 minutos?
Por que todo número elevado a zero é 1?
Por que (-1) . (-1) = 1?

Essas afirmações estão presentes nos livros didáticos adotados pela rede pública e privada e são aceitas sem muitos questionamentos, pelo fato de serem sustentadas pela Matemática Acadêmica.

No caso da Matemática Escolar, há dois aspectos fundamentais que modificam significativamente o papel do rigor nas demonstrações. O primeiro refere-se ao fato de a validade dos resultados matemáticos, que serão apresentados aos estudantes no processo de ensino-aprendizagem, não ser colocada em dúvida; ao contrário, já está garantida pela própria Matemática Acadêmica. O segundo aspecto diz respeito à aprendizagem; neste caso, o mais importante é o desenvolvimento de uma prática pedagógica que assegure a compreensão dos conteúdos matemáticos essenciais, assim como a construção de justificativas que permitam ao jovem estudante utilizá-los de maneira coerente e conveniente, tanto na vida escolar quanto na cotidiana.

Os exemplos de questionamentos são respondidos em sala de aula com o auxílio de uma linguagem que traduz a ideia complexa existente na questão e que leva o aluno a compreender minimamente o conceito matemático presente. Segundo Chervel (1990) apud Valente (2012), excluir a pedagogia do estudo dos conteúdos é condenar-se a nada compreender do funcionamento real dos ensinos. A pedagogia, longe de ser um lubrificante espalhado sobre o mecanismo, não é senão um elemento desse mecanismo; aquele que transforma os ensinos em aprendizagens.

Na pandemia houve um aumento considerável de canais na internet com a proposta de facilitar o aprendizado em matemática. Esses canais recorrem ao uso de uma linguagem simples e sem a rigidez do formalismo acadêmico. Que podemos associar ao uso da matemática escolar. Conforme Rosa (2016), através da plataforma digital Youtube, muitos professores disponibilizam vídeos e web aulas que podem ser acessadas para o ensino da matemática e em sua maioria são de fácil compreensão dos alunos.

Estes canais que adotam essa postura simples e às vezes informal, de comunicar o saber matemático acabam atraindo o interesse dos alunos para tentar suprir as dificuldades encontradas na sala de aula e até mesmo no material didático fornecido, por conta de uma linguagem distante. Diversos autores têm defendido o uso das mídias sociais (como o Youtube) como instrumento de ensino e de aprendizagem. Isso porque as mídias sociais, enquanto ferramenta de comunicação por meio da web, permitem criar e transmitir facilmente o conteúdo na forma de palavras, imagens, vídeos e áudios (SAFKO; BRAKE, 2010).

3. Levantamento de Dados

Na ocasião desta pesquisa, verificou-se oportuna a realização de um levantamento dos dois últimos fluxogramas das matrizes curriculares do curso de Licenciatura em Matemática de duas das universidades estaduais do Ceará. A Figura 1 apresenta o quantitativo de disciplinas da Matemática Escolar e da Matemática Acadêmica nos fluxogramas de 2008 e 2019 da Universidade Estadual do Ceará (UECE). A Figura 2 mostra esses números nos fluxogramas de 2012 e 2018 da Universidade Estadual Vale do Acaraú (UVA).

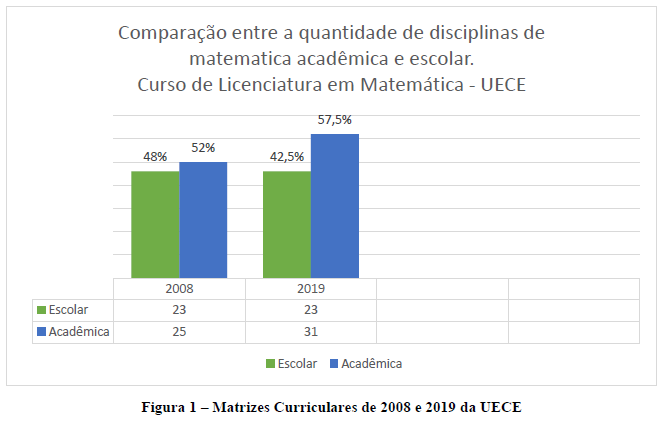
Observando a divisão das disciplinas em Acadêmica e Escolar, percebe-se a existência de uma diferença pequena no quantitativo entre ambas. Destaca-se, no gráfico da Figura 1, o aumento do número de disciplinas de Matemática Acadêmica. Quando observamos o ano de 2008, verificamos uma pequena diferença entre o quantitativo de disciplinas voltadas para Matemática Acadêmica e Escolar. Em relação a formação dos professores e ensino de matemática, acreditamos que este equilíbrio contribua para o desenvolvimento profissional, visto que, no ambiente escolar a parte didática e pedagógica ocupa um espaço muito abrangente. E com a implantação da BNCC, o professor cada vez mais precisa orientar o ensino sob uma base pedagógica que permita o alunos compreender o conhecimento matemático.

Portanto, a BNCC orienta-se pelo pressuposto de que a aprendizagem em Matemática está intrinsecamente relacionada à compreensão, ou seja, à apreensão de significados dos objetos matemáticos, sem deixar de lado suas aplicações. Os significados desses objetos resultam das conexões que os alunos estabelecem entre eles e os demais componentes, entre eles e seu cotidiano e entre os diferentes temas matemáticos. (BNCC, página 276)

Quando comparamos a distribuição das disciplinas do curso em Acadêmica e Escolar, verifica-se que existe uma diferença pequena em relação a matriz de 2012, com leve tendência para Matemática Acadêmica. Já quando comparamos a matriz de 2018, observamos o aumento dessa diferença que acaba tomando o direcionamento para disciplinas Acadêmicas. No processo de formação dos professores, uma matriz equilibrada é de suma importância para que o desenvolvimento profissional, onde o ensino da matemática na escola demanda didática, metodologia diversificada e conhecimento da orientação da BNCC em relação ao processo de ensino. Com isso, destaco a relevância da Educação Matemática para que o processo de ensino com a utilização da Matemática Escolar obtenha êxito.

Consoante Miguel e Miorim (2004) a finalidade da Educação matemática é fazer o estudante compreender e se apropriar da própria Matemática “concebida como um conjunto de resultados, métodos, procedimentos, algoritmos etc.” Outra finalidade apontada pelos autores é fazer o estudante construir, “por intermédio do conhecimento matemático, valores e atitudes de natureza diversa, visando à formação integral do ser humano e, particularmente, do cidadão, isto é, do homem público”.

Discutir, debater e analisar a BNCC, em cursos de licenciatura trará enorme contribuição para o ensino e a aprendizagem da matemática. A Educação Matemática toma como ponto de partida o cuidado com o aluno, considerando sua realidade histórica e cultural e possibilidades de vir a ser; cuidado com a Matemática, considerando sua história e modos de manifestar-se no cotidiano e na esfera científica; cuidado com o contexto escolar, lugar onde a educação escolar se realiza. (BICUDO, 1999).

Portanto, é fundamental preservar a articulação, proposta nesta BNCC, entre os vários campos da Matemática, com vistas à construção de uma visão integrada de Matemática e aplicada à realidade. Além disso, é importante que os saberes matemáticos, do ponto de vista pedagógico e didático, sejam fundamentados em diferentes bases, de modo a assegurar a compreensão de fenômenos do próprio contexto cultural do indivíduo e das relações interculturais. (BNCC, página 542). Segundo Diretrizes Curriculares Nacionais para os Cursos de Matemática, Bacharelado e Licenciatura, os cursos de Licenciatura em Matemática tem como objetivo principal a formação de professores para a educação básica. Os conteúdos descritos a seguir, comuns a todos os cursos de Licenciatura, podem ser distribuídos ao longo do curso de acordo com o currículo proposto pela IES:

· Cálculo Diferencial e Integral
· Álgebra Linear
· Fundamentos de Análise
· Fundamentos de Álgebra
· Fundamentos de Geometria
· Geometria Analítica

A parte comum deve ainda incluir:

a) conteúdos matemáticos presentes na educação básica nas áreas de Álgebra, Geometria e Análise;

b) conteúdos de áreas afins à Matemática, que são fontes originadoras de problemas e campos de aplicação de suas teorias;

c) conteúdos da Ciência da Educação, da História e Filosofia das Ciências e da Matemática.

Para a licenciatura serão incluídos, no conjunto dos conteúdos profissionais, os conteúdos da Educação Básica, consideradas as Diretrizes Curriculares Nacionais para a formação de professores em nível superior, bem como as Diretrizes Nacionais para a Educação Básica e para o Ensino Médio. Desde o início do curso e licenciando deve adquirir familiaridade com o uso do computador como instrumento de trabalho, incentivando-se sua utilização para o ensino de matemática, em especial para a formulação e solução de problemas. É importante também a familiarização do licenciando, ao longo do curso, com outras tecnologias que possam contribuir para o ensino de Matemática.

4 Conclusão

A Matemática sempre estará presente na vida e no desenvolvimento da sociedade, não apenas como uma mera ferramenta, mas como substância que fornece criatividade e técnica para consolidação do conhecimento necessário à sua época.

A pesquisa realizada propicia a conclusão de que fora alcançado o objetivo de estabelecer uma análise sobre as contribuições que a Matemática Acadêmica e a Matemática Escolar fornecem para a formação e atuação do professor, que facilitam a aprendizagem do aluno, com definições mais descritivas e uso de metodologias que visem comunicar o conhecimento matemático de uma forma objetiva e prática.

Logo, aprimorar a formação dos professores é de suma importância, tendo em vista que a qualidade da transposição do conhecimento matemático passa diretamente por uma boa formação, que possibilite uma visão aguçada diante das inúmeras possibilidades para transferir o conhecimento, aplicando-o de forma prática e contextual, diminuindo assim a distância que existe entre a abordagem teórica e a prática. Sem dúvida, o professor é peça fundamental e necessária nesse processo, que exige dele cada vez mais habilidade para estabelecer conexões entre o conhecimento acadêmico e o conhecimento escolar. A matemática vem ocupando cada vez mais espaço, com divulgação e participação em olimpíadas, crescimento de ferramentas digitais, canais no YouTube e a exigência em avaliações de larga escala. Sendo assim, refletir sobre o ensino da matemática se faz sempre necessário para que haja uma boa comunicação, com clareza e relevância para o estudante.

Portanto, a relação da Matemática Acadêmica e Escolar não estabelece um dualismo, uma disputa ou rivalidade. Tal relação acaba por proporcionar reflexões sobre as contribuições que podemos extrair de ambas, provocar à busca por uma formação continuada que contribua para ensino da matemática, destacando a importância de se fazer o uso correto desse binômio para compreensão dos problemas encontrados no processo de ensino e aprendizado e a superação dos desafios que surgem no ambiente escolar.

Assim pode-se gerar uma visão sem estigmas em relação à matemática. Criar grupos de estudos voltados para a discussão da existência dessas duas concepções, com o propósito de fortalecer reflexões e análises que possam contribuir com o desenvolvimento do formando, organizar fóruns e debates com professores com níveis de experiência diferentes em relação ao tempo de docência na educação básica seria de grande valia para compartilhar e enriquecer o processo de formação do estudante de licenciatura em matemática.

Finalmente, conclui-se este trabalho evidenciando a certeza que a matemática nunca deixará de ser um campo fértil para que boas ideias sejam produzidas, um instrumento eficaz para nos mostrar que, realmente, mesmo sendo professores, ainda temos algo a aprender.

REFERÊNCIAS

BICUDO, M. A. V. Ensino de Matemática e Educação Matemática: algumas considerações sobre seus significados. BOLEMA, Rio Claro (SP), v. 12, n. 13, 1999.

BRASIL. Ministério da Educação. Secretaria de Educação Fundamental. PCNS – PARÂMETROS CURRICULARES NACIONAIS: Matemática. Brasília: MEC, 1997.

CHERVEL, A. História das disciplinas escolares: reflexões sobre um campo de pesquisa. TEORIA & EDUCAÇÃO, Porto Alegre, v. 2, n. 2, p. 177-229, 1990.

FELICETTI, V. L. Linguagem na Construção Matemática. REVISTA EDUCAÇÃO POR

ESCRITO – PUCRS, v. 1, n. 1, p. 31-43, jun. 2010.

FIORENTINI, D.; OLIVEIRA, A. T. C. C. O Lugar das Matemáticas na Licenciatura em Matemática: que matemáticas e que práticas formativas? BOLEMA, Rio Claro (SP), v. 27, n. 47, p. 917-938, dez. 2013.

FIORENTINI, D. e LORENZATO, S. INVESTIGAÇÃO EM EDUCAÇÃO MATEMÁTICA: PERCURSOS TEÓRICOS E METODOLÓGICOS. Campinas, SP: Autores Associados, 2006.

FIORENTINI, D.; NACARATO, A. M.; FERREIRA, A. C.; LOPES, C. A. E.; FREITAS, M. T. M.; MISKULIN, R. G. S. Formação de professores que ensinam Matemática: um balanço de 25 anos da pesquisa brasileira. EDUCAÇÃO EM REVISTA, Belo Horizonte, n. 36, dez. 2002.

GARCIA, J. Indisciplina na escola. REVISTA PARANAENSE DE DESENVOLVIMENTO, Curitiba, n. 95, jan./abr. 1999.

JARDIM, V. B. F.; RIBEIRO, A. J.; AGUIAR, M. A matemática acadêmica e seu papel na formação do professor. In: IV SIMPÓSIO PEHCM UFABC, Santo André, nov. 2022.

LIMA, A. L.; BELMAR, C. C. Dificuldades Apresentadas por Professores de Matemática em Início de Carreira: Um Estudo Exploratório. In: XII ENCONTRO NACIONAL DE EDUCAÇÃO MATEMÁTICA, ENEM, São Paulo, jul. 2016.

LORENZATO; S. PARA APRENDER MATEMÁTICA. 2. ed. rev. Campinas, SP: Autores Associados, 2008.

MACEDO, A. D. R.; LINS, A. F. Um Olhar Voltado à Docência, às Práticas em Sala de Aula e à Formação Inicial de Professores de Matemática. REVISTA EDUCAÇÃO MATEMÁTICA EM FOCO, v. 3, n. 1, p. 30 – 45, jan./jun. 2014.

MIGUEL, A.; MIORIM, M. A. História na educação matemática: propostas e desafios. Belo Horizonte: Autêntica, 2004.

MOREIRA, P. C. 3+1 e suas (In)Variantes (Reflexões sobre as possibilidades de uma nova estrutura curricular na Licenciatura em Matemática). BOLEMA, Rio Claro (SP), v. 26, n. 44, p. 1137-1150, dez. 2012.

MOREIRA, P. C.; DAVID, M. M. M. S. Matemática Escolar, Matemática Científica, Saber Docente e Formação de Professores. ZETEKITÉ, v. 11, n. 19, p. 57-80, 2003.

MOREIRA, P. C.; DAVID, M. M. Matemática Acadêmica e Matemática Escolar: Dissonâncias e Conflitos. 40 ANOS DE PESQUISA EM EDUCAÇÃO, Editora UFMG, 2011.

NASCIMENTO, D. T.; SANTOS, E. G. Matemática Acadêmica x Matemática Escolar. In: XI ENCONTRO PARAIBANO DE EDUCAÇÃO MATEMÁTICA, EPBEM, João Pessoa, nov. 2021.

UTSUMI, L. M. S.; SILVA, A. C. Práticas Pedagógicas de Professores de Matemática dos Anos Iniciais do Ensino Fundamental: um estudo sobre a relação entre seus saberes e as orientações curriculares da BNCC. REVISTA BRASILEIRA DE HISTÓRIA, EDUCAÇÃO E MATEMÁTICA (HIPÁTIA), v. 6, n. 1, p. 1-17, 2021.

VALENTE, W. R. O que é número? Produção, circulação e apropriação da Matemática Moderna para crianças. BOLEMA, Rio Claro (SP), v. 26, n. 44, p. 1417 – 1441, dez. 2012.

ROSA, E. F. S. O USO DA INTERNET PARA O ENSINO DA MATEMÁTICA. 24 p. Trabalho de Conclusão de Curso (Graduação em Matemática) – Universidade Federal de São João Del-Rei, São João Del-Rei, 2016.

SANTANA, G.; FERREIRA, A. C. O PROFESSOR DE MATEMÁTICA EM INÍCIO DE CARREIRA: DESAFIOS E ENFRENTAMENTOS. Editora UFOP, Ouro Preto, 2016.

SILVA, M. R. S. COMPETÊNCIAS E A FORMAÇÃO DE PROFESSORES DE MATEMÁTICA: Uma revisão literária nas concepções e implicações na Base Nacional Comum Curricular – BNCC. 46 p. Trabalho de Conclusão de Curso (Graduação em Matemática) – Universidade Federal de Pernambuco, Caruaru, 2023.

VILELA, D; MENEGHETTI, R. C. G. Transposição didática ou práticas matemáticas específicas? O caso do número ordinal e cardinal. EDUC. MATEM. PESQ., São Paulo, v.13, n.1, p. 179-196, 2011.

WASSERMAN, N. H.; WEBER K.; FUKAWA-CONNELLY T.; MCGUFFEY W. Designing advanced mathematics courses to influence secondary teaching: fostering mathematics teachers’ “attention to scope”, JOURNAL OF MATHEMATICS TEACHER EDUCATION, 2019.

(https://impa.br/noticias/artigo-debate-formacao-de-professores-de-matematica/)