REGISTRO DOI: 10.69849/revistaft/ni10202409281605
Luan Pablo Dantas Castroixa1; Prof. Dr. Élida de Paula Moraes Corveloni2; Prof. Dr. Elizângela Veloso Saes3; Prof. Dr. Sandra Cristina Marchiori de Brito4
Resumo
Esta pesquisa ação apresenta os resultados da sintonia dos parâmetros de um controlador PI a partir da identificação do modelo dinâmico do controle de um ventilador em uma unidade de esmagamento de soja. A função de transferência da unidade foi obtida pelo método da Curva de Reação do Processo, por meio da aplicação de uma perturbação em degrau na variável controlada (rotação do ventilador). Esta alteração contribuiu significativamente para a redução de defeitos e desvio padrão de umidade, trazendo maior estabilidade no processo de esmagamento de soja.
Palavras-chave: Sintonia de controladores; Controlador PID; Esmagamento de Soja.
Abstract
This action search presents the results of tuning the parameters of a PI controller based on identifying the dynamic model for controlling a fan in a soybean crushing unit. The unit’s transfer function was obtained using the Process Reaction Curve method, by applying a step disturbance to the controlled variable (fan speed). This change contributed significantly to the reduction of defects and standard deviation of moisture, bringing greater stability to the soybean crushing process.
Keywords: Controller tuning; PID controller; Soybean crushing.
1. Introdução
Nas últimas décadas, houve um progresso significativo na aplicação da tecnologia em várias esferas do conhecimento humano. A automação, do latim Automatus, que significa mover-se por si, é a aplicação de técnicas, softwares e/ou equipamentos específicos em uma determinada máquina ou processo industrial, com o objetivo de aumentar a sua eficiência, maximizar a produção com o menor consumo de energia e/ou matérias primas, menor emissão de resíduos de qualquer espécie, melhores condições de segurança, seja material, humana ou das informações referentes a esse processo, ou ainda, de reduzir o esforço ou a interferência humana sobre esse processo ou máquina (AMÉRICO; AZEVEDO; SOUZA, 2011).
O fato de o uso da automação nos setores industriais ter crescido consideravelmente resultou em melhoria na qualidade e na quantidade da produção e ainda em preços mais baratos. A automação também leva à eficiência, uma vez que torna as empresas mais produtivas no mercado, porque a concorrência exige que a produtividade e a qualidade de seus produtos sejam intensificadas enquanto reduz os custos de produção. Além disso, para atender às demandas diversificadas dos consumidores e à tendência de redução gradual da vida útil dos produtos, busca-se ampliar a flexibilidade na utilização dos sistemas produtivos (MAITELLI, 2003).
Um recurso crucial para a automação industrial é a aplicação de controladores de processos contínuos. Esses dispositivos são responsáveis por manter as variáveis de um processo em valores prédefinidos, conhecidos como set-points, por meio de um algoritmo geralmente proporcional a uma ou mais variáveis medidas em tempo real por um equipamento de controle, geralmente baseado em microprocessador. O controlador do tipo Proporcional-Integral-Derivativo (PID) ainda é amplamente predominante na indústria atualmente. Mais de 90% de todas as malhas de controle existentes são do tipo PI/PID, abrangendo uma ampla gama de aplicações, incluindo controle de processos, acionamentos de motores, setor automotivo, controle de voo, pilotos automáticos, instrumentação industrial, entre outros (ASTROM; HAGGLUND, 2001). Essa popularidade se deve principalmente à facilidade de ajuste dos parâmetros para alcançar um bom desempenho e à disponibilidade desse algoritmo em praticamente todos os equipamentos de controle industrial. Apesar das variações na implementação prática desse algoritmo dependendo do fabricante, a essência do controlador PID permanece a mesma (ISERMANN, 1989).
Devido à ampla utilização do controle PID em processos industriais, diversas técnicas foram desenvolvidas para ajustar os parâmetros proporcionais, integrais e derivativos. Esse desafio é conhecido como o problema de sintonia. As primeiras diretrizes para sintonizar esses controladores foram propostas por Ziegler e Nichols (1942). Essas diretrizes foram significativas devido à sua inovação e à sua simplicidade de aplicação, apesar de apresentarem limitações em termos de desempenho alcançado. Desde então, várias outras regras de sintonia e métodos de projeto foram propostos, desde as de Cohen & Coon até o método Fuzzy (CAMPOS e TEIXEIRA, 2006).
Aproveitando-se deste cenário, o mal condicionamento e secagem da soja em indústrias de extração de óleo não apenas comprometem a qualidade do produto final, mas também afetam negativamente todo o processo produtivo. A umidade inadequada da soja é um dos principais vilões nesse cenário, pois afeta diretamente a qualidade do óleo e a eficácia do processo.
Este trabalho tem como objetivo identificar a dinâmica (função de transferência) do controle de ventilação para secagem de soja em um condicionador e secador de soja em uma indústria de esmagamento de soja com capacidade diária de 3700 toneladas por dia. Em seguida, será empregada a técnica de sintonia pelo método Cohen & Coon (1953) para determinar os parâmetros do controlador PI. Os dados serão coletados por sensor de umidade online TEWS que será utilizado no controlador e enviados ao banco de dados AVEVA PI System de forma a facilitar o manejo e análise dos dados, onde posteriormente na seção de resultados, será realizada a comparação entre o controle manual por um operador e o controle PI, avaliando o desempenho da malha de controle no controle de umidade da soja em relação a um operador experiente.
2. Referencial teórico
Os procedimentos industriais abrangem uma ampla gama de produtos e demandam um controle rigoroso sobre os resultados obtidos. Geralmente, os setores industriais mais dependentes de instrumentação são os relacionados ao petróleo, química, petroquímica, alimentos, cerâmica, siderurgia, celulose e papel, têxtil e geração de energia elétrica. Em todos esses processos, é essencial manter sob controle e estabilidade as variáveis-chave, como pressão, nível, vazão, temperatura, pH, condutividade, velocidade, umidade e concentração. Os dispositivos de medição e controle permitem manter e regular essas variáveis de maneira mais precisa do que se fossem controladas manualmente pelos operadores (FAVARO, 2012).
O sistema de controle tem como objetivo manter a variável controlada em um valor específico. Ele realiza isso ao comparar o valor da variável medida, ou a condição a ser controlada, com o valor desejado (ponto de ajuste), e fazendo ajustes com base na diferença entre esses dois valores, tudo isso sem precisar de intervenção manual por parte do operador (BEGA et al, 2006).
Os sistemas de controle se dividem em malha aberta e malha fechada. Na malha aberta, a saída não influencia o sinal de controle, e não há comparação entre a saída do processo e a saída de referência. Nesse tipo de controle, a saída não é comparada com a entrada de referência, resultando em uma condição de funcionamento fixa para cada valor de saída. Contudo, na presença de perturbações, o sistema pode não alcançar os objetivos desejados. O controle em malha aberta só é recomendado em sistemas com uma relação bem conhecida entre entrada e saída, e sem perturbações internas ou externas significativas. Na prática, a ação de controle é independente da saída (OLIVEIRA, 1999).
A Figura 1 apresenta o diagrama que ilustra um sistema de malha aberta em blocos.

FIGURA 1: Diagrama de blocos de um sistema de controle em malha aberta. Fonte: Oliveira (1999).
No controle em malha fechada, o sinal de saída influencia diretamente na ação de controle, sendo chamado de sistema com realimentação ou retroação (feedback). Aqui, o sinal de erro, que é a diferença entre os valores de referência e de realimentação (que pode ser o sinal de saída ou uma função dele), é utilizado para ajustar o controlador, reduzindo o erro e mantendo a saída do sistema no valor desejado pelo operador. Em um sistema típico de malha fechada, a relação entre entrada e saída é representada conforme a Figura 2 (OLIVEIRA, 1999).
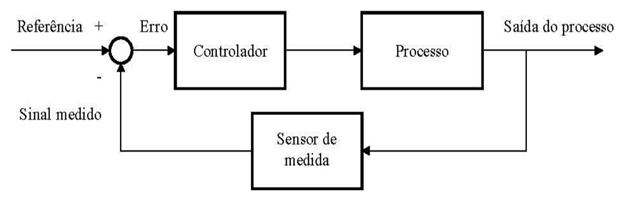
FIGURA 2: Diagrama de blocos de um sistema de controle em malha fechada. Fonte: Oliveira (1999).
Atualmente, há controladores de processos contínuos que empregam uma variedade de técnicas de controle, incluindo Proporcional-Integral-Derivativo (PID), PID adaptativo (não linear), Lógica Fuzzy, Controle Preditivo, entre outros (BEQUETTE, 2003).
O algoritmo Proporcional-Integral-Derivativo (PID) é amplamente utilizado na indústria devido ao seu desempenho robusto em diversas condições de operação e à sua simplicidade funcional, que permite aos engenheiros e técnicos operá-lo de forma direta. Como o nome sugere, o PID é composto por três coeficientes – proporcional, integral e derivativo – que são ajustados para alcançar a resposta ideal (MAITELLI, 2003).
2.1 Definições básicas dos termos do controlador
Bega et al. (2006) destacam três termos essenciais associados a qualquer processo: a Variável controlada que se refere à condição que se pretende manter de um determinado parâmetro de processo, como nível, vazão, pressão, temperatura, entre outros, o Valor desejado (set point – SP) que é o ponto de referência para cada variável que se deseja manter, e a Variável manipulada: é aquela que influencia diretamente a variável controlada e pode ser ajustada conforme necessário. Em sistemas de controle simples, geralmente há uma variável manipulada para cada variável controlada. No entanto, em sistemas mais complexos, pode haver mais variáveis controladas do que manipuladas.
Ademais, há a presença de distúrbios que tendem a desviar as variáveis controladas do valor desejado. Portanto, a função do sistema de controle é ajustar a variável manipulada de modo a manter a variável controlada no valor desejado (set point), mesmo na presença de distúrbios eventuais (BEGA et al., 2006).
2.2 Controlador PID
O controlador PID é caracterizado pela incorporação das ações proporcional, integral e derivativa (BEGA et al., 2006).
2.2.1 Ação Proporcional
Neste tipo de controlador, a relação entre o sinal de saída e o erro é expressa pela Equação 1 (OLIVEIRA, 1994).
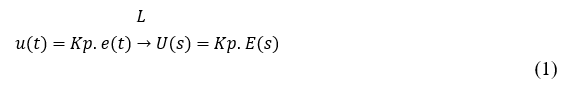
Onde u(t) representa a saída do controlador, Kp é o ganho proporcional, e e(t) é o erro da variável do processo dado por e(t) = ysp – y(t), onde ysp é o set-point e y(t) é a saída do sistema. O termo L indica a transformação da equação do domínio do tempo (t) para o domínio de Laplace (s).
2.2.2 Ação Proporcional-Integral
Quando a saída do controlador é uma função do erro e da integral do erro, temos um controlador proporcional-integral, conforme expresso na Equação 2. O diagrama de blocos da ação proporcionalintegral do PID é apresentado na Figura 5 (OLIVEIRA, 1994).
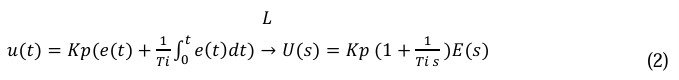
Onde, Ti é o tempo integral.
2.2.3 Ação Proporcional-Integral
O controlador proporcional-integral-derivativo combina as características de estabilidade fornecidas pelo controle proporcional mais derivativo com as características de eliminação de erro oferecidas pelo controle proporcional mais integral. Essas particularidades são, portanto, integradas em um único controlador (MARLIN, 1995). A saída do controlador é expressa pela Equação 3.
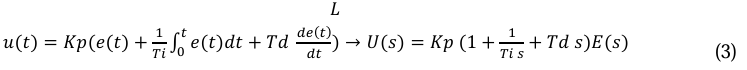
Onde, Td é o tempo derivativo.
A Figura 3 ilustra as curvas de resposta das três ações de controle, P, PI e PID, em um sistema de malha fechada. Isso permite a análise do efeito de cada ação na resposta do sistema de controle, em relação ao tempo (OLIVEIRA, 1994).
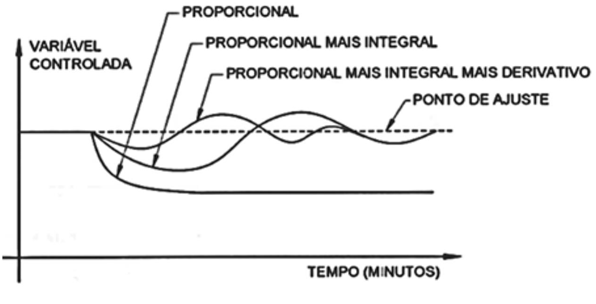
FIGURA 3: Resposta de um controlador PID. Fonte: BEGA et al, (2006).
2.3 Sintonia baseada na resposta em malha aberta
As técnicas de ajuste em malha aberta geralmente se fundamentam na curva de reação do processo, que é a resposta deste a uma perturbação em degrau na variável manipulada na saída do controlador (BEGA et al., 2006). A maioria dos métodos de ajuste em malha aberta baseia-se na aproximação da curva de reação do processo à resposta de um sistema mais simples. Uma abordagem comum é aproximar o sistema a um modelo de primeira ordem com tempo morto (COUGHANOWR & KOPPEL, 1978). A figura 4 ilustra esse procedimento, considerando a curva de reação do processo a uma perturbação (∆X) em degrau na saída do controlador.
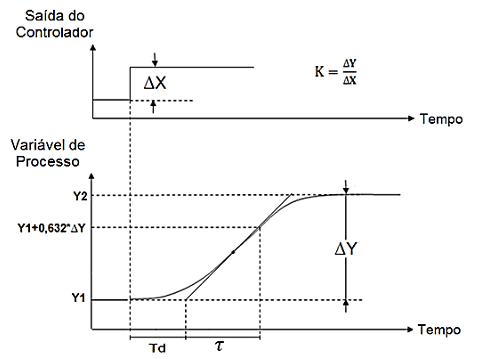
FIGURA 4: Curva de reação do processo a um degrau na saída do controlador. Fonte: BEGA et al, (2006).
A curva exibe um retardo inicial na resposta da variável Y do processo, indicando uma baixa velocidade de resposta. Apresenta um ponto de inflexão, seguido de um aumento gradual até tender para um valor final Y2, indicando estabilização. Para determinar os parâmetros do controlador, traça-se uma tangente à curva no ponto de inflexão. Com isso, são obtidos os parâmetros gráficos K, T e Td, que são utilizados para calcular os parâmetros dos controladores conforme as relações descritas na tabela 1 (COHEN & COON, 1953).

TABELA 1: – Parâmetros do controlador PID pelo Método Cohen & Coon. Fonte: COHEN & COON, (1953).
3. Desenvolvimento
Esta pesquisa-ação tem propósito exploratório com natureza de pesquisa aplicada, em que utiliza-se de uma abordagem quantitativa, podendo ser subdividido em quatro etapas distintas. Inicialmente, ocorre a fase de ambientação com a planta piloto. Em seguida, procede-se à modelagem por meio da identificação da dinâmica da planta. Posteriormente, passa-se à elaboração dos algoritmos de controle, utilizando o software Loop-Pro Control para determinar os parâmetros do controlador PID, de modo a agilizar os cálculos. Por fim, conclui-se com a etapa de levantamento das curvas de resposta do sistema e análise dos resultados experimentais, incluindo a comparação do desempenho da malha ao invés de um operador experiente.
3.1 Descrição do processo
O ventilador a ser controlado está ligado ao secador condicionador, a partir dele, temos o controle da umidade da soja de saída do equipamento. Quanto maior a velocidade do ventilador, mais umidade é retirada da soja. O monitoramento da umidade será realizado por um sensor online na saída do secador condicionador, e ele será nossa variável controlada.
A figura 5 representa o diagrama de blocos do processo.
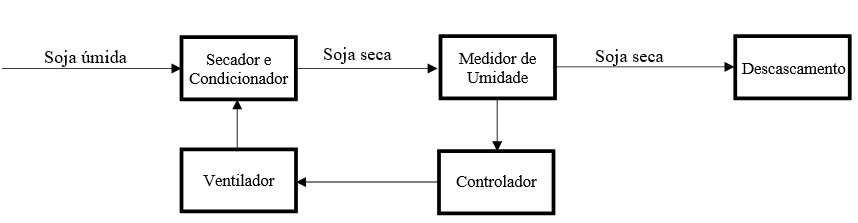
FIGURA 5: Diagrama de blocos do processo. Fonte: Autoria própria, (2024).
3.2 Curva de reação do processo
Para identificar o modelo dinâmico do processo, empregou-se o método da Curva de Reação do Processo em malha aberta. Nesse procedimento, uma perturbação em degrau foi introduzida na variável manipulada (no caso, a rotação do ventilador). Em seguida, utilizou-se o software Loop-Pro para identificar a curva e ajustar os valores de sintonia do controlador PID. A figura 6 representa a alteração na variável (degrau) e a resposta da umidade.
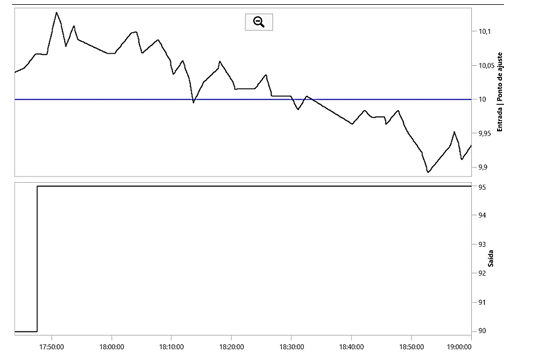
FIGURA 6: Perturbação em degrau na variável. Fonte: Loop-Pro, (2024).
3.3 Sintonia do controlador
A partir do modelo do processo, o software Loop-Pro gerou os valores de ganho proporcional, e tempo integral. O ganho derivativo não foi utilizado a pedido da supervisão da empresa. Na figura 7, temos a modelagem dos dados e os valores do ganho proporcional 32,65 e tempo integral 655,8.
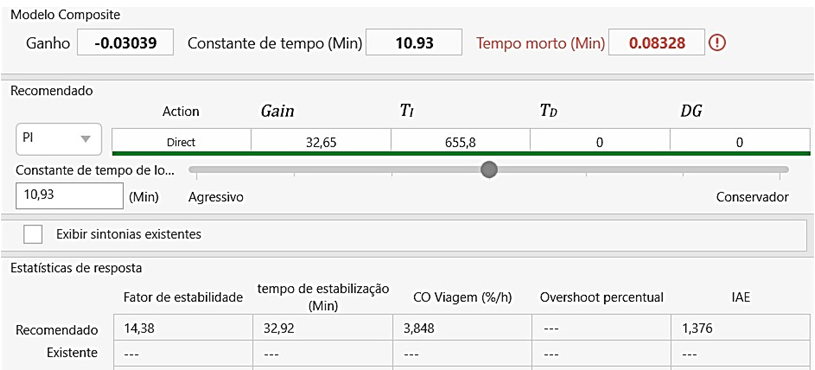
FIGURA 7: Obtenção dos valores de ganho proporcional e tempo integral. Fonte: Loop-Pro, (2024).
Conforme observado, foi utilizada uma abordagem moderada para os valores do controle PI a pedido da supervisão. Os valores serão inseridos no controlador, e o processo de controle será observado por um mês. O valor inserido no controlador de set point é de 10.0, sendo este a umidade ideal para a soja.
4. Resultados
A coleta de dados durou 30 dias após o comissionamento do controlador, em que, foi coletado a média de intervalos de uma em uma hora, gerando 720 amostras. Este compilado de amostras foram comparados com 720 amostras com médias de uma em uma hora do período anterior ao comissionamento do controlador, onde os ajustes eram guiados pelo operador experiente. Esta comparação foi realizada no software Minitab por meio de um teste T, com limites de 9,8% e 10,2%. A figura 8 ilustra os resultados.

FIGURA 8: Resultados. Fonte: Minitab, (2024).
Os resultados se mostraram promissores, com redução de 0,126 no desvio padrão, e 57% de redução de defeitos de umidade para resultados entre 9,8% e 10,2%. Com isso, o teste atingiu os resultados esperados, promovendo maior estabilidade ao processo e um melhor condicionamento da soja.
5. Conclusão
A instalação do sistema de controle proporcional-integral (PI) no equipamento de secagem de soja trouxe melhorias notáveis, superando até mesmo a gestão de um operador experiente. Esse sistema permitiu uma diminuição considerável do volume de soja defeituosa, além de aprimorar de forma geral o processo de secagem. Com o uso do controle PI, foi possível alcançar uma resposta muito mais precisa e uniforme a flutuações nas condições de operação, resultando em uma secagem mais homogênea e eficaz da soja. O sistema também introduziu uma maior confiabilidade e estabilidade operacional, ao reduzir a necessidade de intervenção manual e diminuir as chances de erros na operação. Em síntese, a implementação do controle PI provou ser uma solução eficiente para otimizar a qualidade do processo de secagem da soja, culminando em produtos finais de melhor qualidade e redução de índices de rejeição.
Como ponto de melhoria identificado, há oportunidade de ajuste no tempo integral para momentos grandes de oscilação na umidade de entrada da soja. Esta melhoria no tempo, diminuirá o tempo de recuperação da umidade, atingindo o set point rapidamente.
Referências
AMÉRICO, I.; AZEVEDO, M. J. G.; SOUZA, A. de. Trabalho automação na metalurgia manual X automatização. 2011. Disponível em: http://www.ebah.com.br/content/ABAAAekoAAJ/trabalho-automacao-na-metalurgia-manualx-automatizado. Acesso em 29 jun. 2024.
ÅSTRÖM, K.J. AND T. HÄGGLUND.The future of PID control. Control Engineering Practice, 2001.
BEGA, Egídio A.; FINKEL, Vitor S.; KOCH, Ricardo; Instrumentação industrial, Instituto Brasileiro de Petróleo e Gás, Rio de Janeiro, 2006.
BEQUETTE, B. Wayne; Process control: modeling, design and simulation. Prentice-Hall. 2003.
COHEN, H.; COON, G. A. Theoretical consideration of retarded control. Trans. Asme, Vol 75, pp. 827-834, 1953.
COUGHANOWR, D.R.; KOPPEL, L.B. Análise e controle de processos. Tradução de Carlos Augusto G. Perlingeiro. Guanabara, Rio de Janeiro. 1978.
FAVARO, Juliana. Controle preditivo aplicado à planta piloto de neutralização de pH. Escola Politécnica, Universidade de São Paulo. São Paulo, 2012.
FREIRE, Hélio; MOURA OLIVEIRA, P. B.; SOLTEIRO PIRES, E. J. From single to many-objective PID controller design using particle swarm optimization. International Journal of Control, Automation and Systems, v. 15, n. 2, p. 918-932, 2017.
ISERMANN, R. Digital Control Systems, Springer Verlag (2ªed), 1989.
MAITELLI, A. L. Controladores lógicos programáveis. Apostila de Controladores Lógicos Programáveis, 2003.
MARLIN, T. E. Process Control. New York: McGraw-Hill, 1995.
OLIVEIRA, J. P. B. M. Review of Auto-tuning Techniques for Industrial Pl Controllers. Dissertação de Mestrado. University of Salford, 1994.
1; 2; 3; 4Engenharia de Produção – UFMS
