REGISTRO DOI: 10.5281/zenodo.11103838
Johnny Luís Mércuri;
Maria Elis Machiavelli do Carmo;
Almiria Messias da Silva;
Hammhwygem Tadach Araujo de Oliveira
Resumo
Neste artigo é apresentado um estudo sobre o número de casos de pessoas infectadas pela COVID-19 na região sudeste brasileira no ano de 2024. Para tal, buscou-se analisar o número de casos de pessoas infectadas em toda região sudeste nas nove primeiras semanas epidemiológicas e com base nos resultados obtidos, aplicar o modelo compartimental SIR (suscetíveis – infectados – recuperados) e gerar algumas curvas ao fixar a taxa de recuperação e variar a taxa de infecção para alguns valores, buscando obter curvas próximas aos valores coletados e tirar conclusões em relação a taxa de transmissão do vírus na população suscetível.
Palavras-chave: Covid – 19, modelo compartimental SIR, simulação SIR.
Abstract
This article presents a study on the number of COVID-19 cases in the Brazilian Southeast region in the year 2024. To do so, an analysis was conducted on the number of infected cases in the entire Southeast region during the first nine epidemiological weeks. Based on the results obtained, the SIR compartmental model (susceptible – infected – recovered) was applied, generating several curves by fixing the recovery rate γ and varying the infection rate β for certain values. The goal was to obtain curves close to the collected values and draw conclusions regarding the virus transmission rate in the susceptible population.
Keywords: Covid – 19, SIR compartmental model, SIR simulation.
1 Introdução
Os modelos compartimentais são ferramentas fundamentais na análise e previsão de fenômenos complexos em diversos campos, desde a epidemiologia até a ecologia e economia. Eles dividem uma determinada população estudada em compartimentos distintos, que descrevem as interações ao longo do tempo por meio de equações diferenciais, permitindo uma melhor compreensão sobre a dinâmica de propagação de algum vírus na população analisada.
Desde sua introdução por Kermack e McKendrick em 1927, o modelo tem sido uma ferramenta amplamente utilizada na propagação de doenças infecciosas, fornecendo uma estrutura conceitual para entender uma variedade de doenças, desde a gripe, sarampo e a mais recente a COVID-19.
Em 2019 o modelo compartimental SIR, subdividido nos compartimentos dos suscetíveis, infectados e recuperados, ganhou notoriedade após sua aplicação na modelagem do comportamento da COVID-19. O modelo descreve a dinâmica da população entre os compartimentos, sendo essa dinâmica, regida por dois parâmetros denotados por e , valores que expressam a taxa de propagação e a taxa de recuperação, respectivamente segundo (BARELLI et al., 2023).
Devido ao esforço mundial no combate a COVID-19, vacinas foram desenvolvidas e o número de pessoas infectadas reduziu significativamente, proporcionando um momento de alívio para os órgãos de saúde de todos os países.
No dia 18/02/2024 o portal do G1 publicou uma notícia com o seguinte título “Covid-19: pesquisadores alertam para possibilidade de nova onda da doença”, a notícia traz um alerta e dados sobre o aumento de casos da COVID-19 no Brasil no ano de 2024, reacendendo os riscos para uma nova onda da doença, aponta (ORTIZ, 2024). Tal fato acende a motivação de se analisar e realizar previsões, mais uma vez, para o número de casos da COVID-19, como uma forma de auxiliar outros estudos e alertar os órgãos de saúde responsáveis no combate a COVID-19.
O presente artigo, tem por objetivo apresentar os resultados obtidos após algumas simulações do número de casos de pessoas infectadas pela COVID-19 na região sudeste brasileira no ano de 2024 nas 9 primeiras semanas epidemiológicas (cada semana equivale a 7 dias). Para gerar os modelos utilizou-se software GeoGebra e com base nos dados coletados, foram geradas algumas previsões gráficas com as variações dos parâmetros ao assumir um fixo.
2 Referencial teórico
O modelo compartimental SIR é subdividido em três compartimentos, o S que representa os indivíduos suscetíveis, o I que representa os indivíduos infectados e o R que representa os indivíduos recuperados. A população total, representada por N, é fixa segundo (TAVARES, 2017, p.2), onde N= S(t)+I(t)+R(t) apresentando a não introdução de novos indivíduos.
TELES (2020) aponta que a taxa de variação dos indivíduos do compartimento S para o compartimento I, depende do número de encontros entre os indivíduos suscetíveis e infectados, que é representada por . A taxa de variação dos indivíduos do compartimento I para o compartimento R, depende da taxa de recuperação dos indivíduos infectado, que é representada por γ.
A seguir, tem-se uma representação do fluxo dos indivíduos de uma dada população N entre os compartimentos do modelo.
Figura 1: Modelo SIR (Suscetíveis – Infectados – Recuperados)
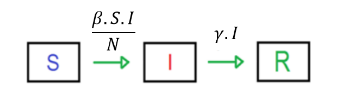
Fonte: Elaborado pelo autor.
No modelo SIR, representado acima, não há reinserção dos indivíduos recuperados no compartimento de suscetíveis, de acordo com (BARELLI et al., 2023) e (TELES, 2020) a variação de indivíduos suscetíveis é representada pela equação diferencial a seguir.
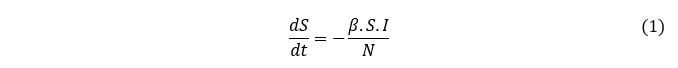
A variação dos indivíduos infectados, segundo com (BARELLI et al., 2023) e (TELES, 2020) é representada pela EDO a seguir.
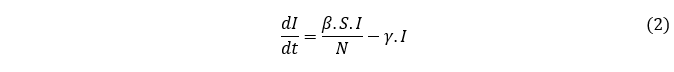
E a variação dos indivíduos recuperados é representada pela equação a seguir, segundo (BARELLI et al., 2023) e (TELES, 2020).
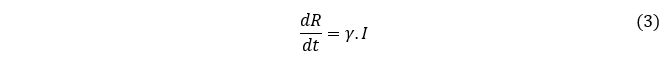
As EDOs (1), (2) e (3) juntas, representam a variação de uma determinada população e o sistema de EDOs a seguir de acordo com (TELES, 2020) descreve o modelo compartimental SIR.
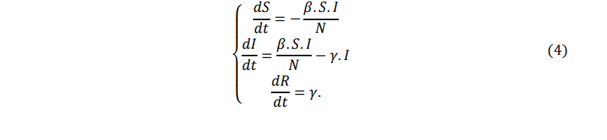
A seguir, tem-se a representação gráfica do sistema apresentado em (4), resolvido de forma numérica utilizando o software GeoGebra, os parâmetros e adotados foram escolhidos aleatoriamente, somente com o objetivo de gerar o gráfico, o valor de N adotado foi 1.
Figura 2: Gráfico do modelo SIR
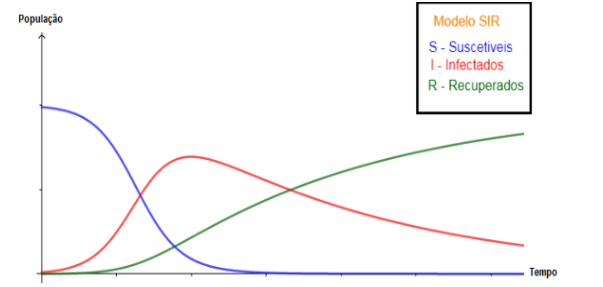
Fonte: Elaborado pelo autor usando o GeoGebra.
3 Materiais e métodos
O presente artigo aborda a pesquisa quantitativa, afim de gerar um modelo matemático para a previsão do número de casos de pessoas infectadas pela COVID-19 na região sudeste do Brasil. Os dados para gerar o modelo foram coletados diretamente do site: “Coronavírus Brasil (saude.gov.br)” na aba “Painel interativo”, após acessar a aba, a plataforma disponibiliza o número de novos casos por semana epidemiológica, sendo esse os valores utilizados para gerar os modelos.
Os dados coletados foram transportados para o software GeoGebra, aplicou-se o sistema de equações do modelo compartimental SIR (4), assumiu-se o valor de N=1. Para os parâmetros e , adotou-se o seguinte critério, fixando o parâmetro γ=0.04 e variando . Para as variações de , buscou-se gerar curvas do compartimento I que se aproximem dos dados reais coletados aplicando o sistema de equações (4) que foi resolvido de forma numérica pelo software utilizado.
A escala gráfica está organizada da seguinte forma, os valores do eixo das abscissas representam os dias, os pontos no plano cartesiano são em relação aos valores das semanas epidemiológicas, intervalos de 7 em 7. Os valores do eixo das ordenadas, representam o número de infectados de acordo com a razão infectados da semana epidemiológica pela população da região sudeste, proporcionando o percentual da população infectada em relação a população do sudeste brasileiro.
Segundo o IBGE, de acordo com o censo de 2022, a população da região sudeste era de 84.840.113, sendo esse valor assumido para a razão apresentada anteriormente. Em relação ao período de coleta, para gerar os modelos, usou-se as 9 primeiras semanas epidemiológica do ano de 2024.
4 Resultados e discussões
As curvas a seguir, apresentam as simulações do sistema de equações (4). Buscou-se obter curvas que se aproximem dos resultados coletados das 9 primeiras semanas epidemiológicas de 2024, do sudeste brasileiro ao se fixar o parâmetro γ=0.04, sendo a curva em rosa onde β=0.09, a em azul onde β=0.10, a em vermelho para β=0.11, a em amarelo com β=0.12 e a em verde para β=0.13.
Figura 3: Modelo SIR com parâmetros variando
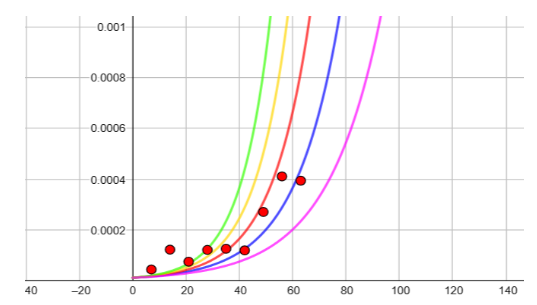
Fonte: Elaborado pelo autor usando o GeoGebra.
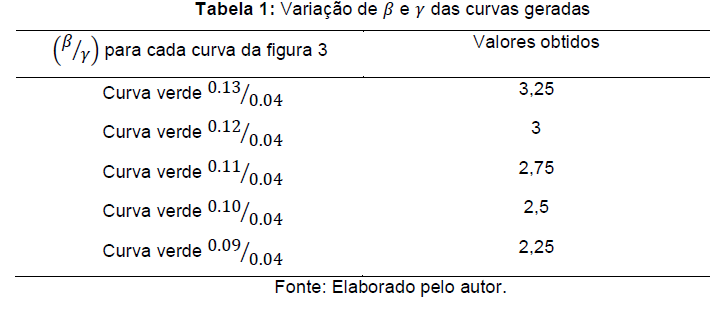
De acordo com os modelos gerados, com base nos dados coletados, a taxa de infectados está-se reduzindo, pois, a partir da quarta semana epidemiológica o número de casos de infectados estão fora da curva em verde, onde a taxa de infecção é de 0.13 . O coeficiente de reprodução basal, segundo (YANG, 2001) é definido por β/y no instante inicial de transmissão, aplicando essa razão para os parâmetros dos modelos gerados, tem-se a tabela a seguir.
A imagem a seguir, traz as curvas dos infectados em relação a figura 3, sem os dados coletados.
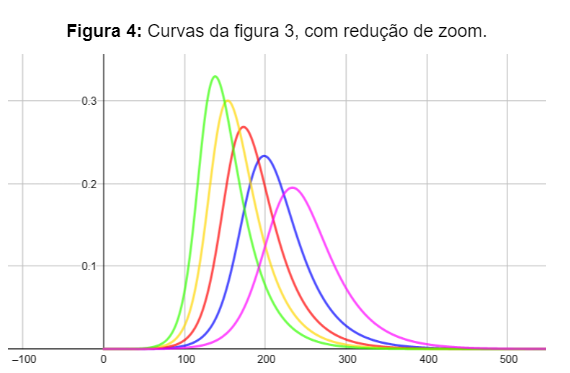
Fonte: Elaborado pelo autor usando o GeoGebra.
5 Conclusão
O objetivo do estudo em questão foi o de realizar previsões da curva de infectados para os casos de pessoas infectadas pela COVID-19 no sudeste brasileiro e tirar algumas possíveis conclusões por meio dos modelos gerados em relação ao comportamento da transmissão na população suscetível.
Para tal, buscou-se aplicar o sistema de equações diferenciais do modelo compartimental SIR (suscetíveis – infectados – recuperados) ao fixar a taxa de recuperação y em 0.04 e variar a taxa de infecção β para alguns valores, aproximando as curvas geradas pelos valores coletados.
Pode-se verificar, de acordo com os modelos gerados e os parâmetros adotados, uma redução na taxa de infectados pela COVID-19 no Sudeste, ao se comparar as 9 primeiras semanas epidemiológicas. Se o número de casos confirmados continuasse seguindo o crescimento da terceira e quarta semana epidemiológica, curva gerada usando β=0.13, aproximadamente após 137 dias (contando a partir do 1 de janeiro) o número de infectados atingiria o pico, tendo aproximadamente 33% de toda população suscetível infectada nesse dia o que causaria uma sobrecarga no sistema de saúde da região sudeste e assim, ocasionando um possível aumento no número de mortes em casos mais graves da doença.
Tomando por base a curva gerada para β=0.10, nota-se uma significativa redução na taxa de propagação ao se comparar com a curva gerada para β=0.13 , para a curva em azul o pico do número de casos ocorreria 234 dias (contando a partir do 1 de janeiro), tendo aproximadamente 19,5% da população suscetível infectada, representando uma significativa redução na taxa de infecção ao comparada a previsão para a taxa de 0.13.
Portanto, de acordo com os modelos gerados e com bases nos dados coletados, pode-se verificar que o número de casos da COVID-19 no sudeste brasileiro continuam subindo, mas apresentou uma redução na taxa de infecção no decorrer das semanas epidemiológicas, verificado ao se comparar as curvas verde e azul geradas pelo modelo. A redução da taxa de infecção traz um significativo alívio, mas não dispensa nossas atenções, visto a letalidade da COVID-19 nos anos de 2020, 2021 e 2022.
Referências
ORTIZ, B.. Covid-19: pesquisadores alertam para possibilidade de nova114 onda da doença. Portal de notícias G1, 2024.115.
CORONAVÍRUS BRASIL. Painel corona vírus. Disponível em: https://covid.saude.gov.br/ . Acesso em: 06/03/2024.
YANG, H. M. Epidemiologia matemática: Estudo dos efeitos da vacinação em doenças de transmissão direta. Editora Unicamp, 2001. 239 f. Campinas.
BARELLI, V. E. G.; BIGARDI, T. M.; MINATOGAU, F. S.. Aplicação do modelo SIR com dinâmica vital no estudo da transmissão da dengue no município de Campinas – SP. Grupo de Biomatemática IMECC – Unicamp, pg. 115-130, Ano: 2023. Disponível em: https://www.ime.unicamp.br/~biomat/Bio33_art8.pdf . Acesso em: 06/03/2024.
TAVARES, J. N.. Modelo SIR em epidemiologia. Revista de Ciências Elementar. V5(02):020. Junho de 2017. Disponível em: https://rce.casadasciencias.org/rceapp/pdf/2017/020/.
TELES, P. Modelos compartimentais e aplicações. Revista de Ciências Elementar. V8(02):024. Abril de 2020. Disponível em: https://rce.casadasciencias.org/rceapp/pdf/2020/024/.
