MATHEMATICAL MODELING AS A TEACHING TOOL IN THE SCHOOL ENVIRONMENT: AN APPLICATION THROUGH THE MAKING OF A MODEL OF A SCHOOL IN THE MUNICIPAL NETWORK OF TERESINA-PI
REGISTRO DOI: 10.5281/zenodo.10667296
Eduardo de Moura dos Santos Silva1
Raimundo Nonato Sousa2
Adriano Faustino de Sousa3
Gildon César de Oliveira4
Roberto Arruda Lima Soares5
Resumo
Levando em consideração as dificuldades encontradas no processo de ensino-aprendizagem de Geometria plana por alunos do ensino fundamental, a presente pesquisa visa investigar as possíveis contribuições que o uso de modelagem matemática como ferramenta de ensino, no ambiente escolar, proporciona no ensino-aprendizagem dos conceitos de perímetro e área. Para tanto, foi proposta uma sequência de atividades didáticas com o intuito de permitir aos alunos a compreensão, através da prática, mediante a confecção da maquete de uma escola da rede municipal de Teresina-PI. Através dessa atividade, buscou-se demonstrar a importância dos conteúdos matemáticos na vida cotidiana, possibilitando, assim, uma aprendizagem significativa aos educandos do 7° do ensino fundamental, também refletir, se a estratégia em questão favorece a construção de conhecimento necessário para o aluno. A pesquisa foi avaliada de forma quantitativa e qualitativa, desenvolvida durante onze encontros. Nestes encontros, foram observadas a motivação promovida pela estratégia aplicada, assim como a efetivação da construção do conhecimento matemático através da experimentação, que possibilitou também o entendimento e significado dos conteúdos matemáticos abordados na pesquisa. Para análise da efetivação dessa metodologia, foram aplicados dois testes. O teste inicial, que buscou investigar o conhecimento prévio dos alunos e o teste final, que analisou os conhecimentos obtidos após a aplicação da sequência didática. Nesses dois testes foram aplicadas questões envolvendo os conteúdos de perímetro e área. Em seguida, foi feita uma comparação dos dados obtidos nesses testes e, por fim, a comprovação de que a metodologia proposta, favorece de forma significativa, a aprendizagem dos alunos, deixando-os motivados, assim como possibilitou a melhoria da concentração dos discentes avaliados.
Palavras-chave: Modelagem Matemática. Aprendizagem. Ambiente Escolar. Maquete.
1 INTRODUÇÃO
Na era digital, um dos maiores desafios dos professores de matemática é apresentar metodologias no ensino que despertem os interesses de seus alunos. Tais metodologias podem ser apresentadas de forma criativa, relacionando os conteúdos estudados com a prática e a vida cotidiana, contribuindo para melhorar a formação do conhecimento em qualquer fase da escolaridade do educando, pois um dos ambientes em que a criança passará um bom tempo do seu viver é a escola (BIEMBENGUT, 2019).
Nesse sentido, uma das maneiras que os professores de matemática podem despertar o interesse dos alunos é usando modelagem matemática no ambiente escolar, propondo desafios que facilitem o entendimento dos conteúdos estudados.
Para isso, o manuseio de materiais que facilitam esse processo é de extrema importância. Nesta perspectiva, a construção de maquetes físicas favorece a visão geométrica e tridimensional dos modelos arquitetônicos. Os processos matemáticos de resolução de problemas. A pesquisa, o desenvolvimento de projeto e a modelagem podem ser considerados formas de atividades favoráveis, razão pelo qual são ao mesmo tempo, objeto e estratégia de aprendizagem ao longo do ensino fundamental (BNCC, 2017, p. 266).
Desta forma, esse processo pode favorecer uma aprendizagem significativa e motivadora para os que participam dessa metodologia de ensino.
Assim, a referida metodologia de ensino se torna atrativa e desperta o interesse dos participantes, melhorando o processo de ensino aprendizagem, pois ela propicia na escola um ambiente de “querer saber” nos anos iniciais da educação básica e, em consonância com as orientações dos Parâmetros curriculares nacionais (PCN) (BIEMBENGUT, 2019).
Além dos aspectos educacionais que a modelagem matemática no ambiente escolar pode proporcionar, temos ainda a gama de conteúdos que os alunos irão ter o contato na atividade proposta, tais como: perímetro, área, razão, proporção, ampliação, redução e unidade de medida.
Para isso, a construção de maquetes físicas é uma forma de modelar os problemas. Ou seja, uma intervenção didática usando modelagem matemática como ferramenta de ensino no ambiente escolar pode proporcionar aos educandos o despertar para a construção e desenvolvimento de seus conhecimentos matemáticos.
Durante minhas experiências, percebi que grande parte dos alunos confundiam muito esses conceitos. Quando era solicitado o perímetro, calculavam a área e quando era solicitada a área, calculavam o perímetro; mostrando que os métodos tradicionais usados não denotavam uma boa aprendizagem, sem considerar as dificuldades apresentadas nas relações entre unidades de medidas.
Assim, a pesquisa foi desenvolvida com o objetivo geral de verificar quais efeitos as intervenções educativas podem proporcionar aos estudantes do 7º ano do ensino fundamental nos conceitos de perímetro e área, utilizando modelagem matemática no ambiente escolar, através da confecção de maquetes.
Pretendeu-se ainda com os objetivos específicos investigar as contribuições que a modelagem matemática, por meio confecção da maquete de uma escola da rede municipal de Teresina, proporciona ao processo de ensino-aprendizagem dos alunos; confeccionar a maquete da escola; avaliar a eficácia do uso de modelagem matemática no ambiente escolar como ferramenta motivadora do ensino; proporcionar uma aprendizagem significativa na perspectiva de reduzir as dificuldades de aprendizagem nas relações de área e perímetro e verificar as contribuições que o uso de modelagem matemática através da confecção de maquete proporciona para os alunos.
2 MODELAGEM MATEMÁTICA
A Modelagem matemática é a ação de fazer modelos através da construção do conhecimento e da pesquisa. Nesse processo, os alunos participam de forma ativa e criativa para melhor compreender os conceitos matemáticos e relacioná-los com a vida cotidiana. Por esse sentido, podemos dizer que é um processo que consiste em traduzir uma situação ou tema do meio em que vivemos para uma linguagem matemática. Essa linguagem, que denominamos Modelo Matemático, pressupõe um conjunto de símbolos e relações matemáticas que representam o fenômeno em questão (BASSANEZI, 1994, p. 01). Isto é importante na formação do conhecimento do aluno, pois a matemática usada na resolução de problemas cotidianos é uma ferramenta poderosa no processo de ensino.
A modelagem matemática no ensino pode ser um caminho para despertar no aluno o interesse por tópicos matemáticos que ele ainda desconhece, enquanto aprende a arte de modelar, matematicamente. Isso porque é dada ao aluno a oportunidade de estudar situações-problema por meio de pesquisa, desenvolvendo o seu interesse e aguçando seu senso crítico. (BIEMBENGUT & HEIN, 2005, p.18).
Historicamente o homem desenvolveu o conhecimento matemático na perspectiva de solucionar problemas de seu cotidiano, arte de expressar situações problema de nosso meio está presente desde os primórdios da nossa história. A representação formal de vivências se deu através da sistematização das ideias presentes na tentativa de solucionar problemas do dia a dia. Portanto, a modelagem matemática é tão antiga quanto a própria Matemática (BIEMBENGUT; HEIN, 2005, p.8).
Segundo Bassanezi (2009, p.16), a modelagem matemática consiste na arte de transformar problemas da realidade em problemas matemáticos e resolvê-los, interpretando suas soluções na linguagem do mundo real. Assim, creio que a modelagem matemática é uma alternativa de ensino que possibilita o despertar de interesse de forma crítica dos alunos para os conteúdos matemáticos.
A aprendizagem realizada por meio da modelagem matemática facilita a combinação de aspectos lúdicos da matemática com seu potencial e aplicações. E mais, com este material, o estudante vislumbra alternativas no direcionamento de suas aptidões ou formação acadêmica. (BASSANEZI, 2002, p. 16).
Isto é a arte de expressar por intermédio de linguagem matemática situação-problema de nosso meio, tem estado presente desde os tempos mais primitivos, ou seja, modelagem matemática surgiu de aplicações na rotina diária dos povos antigos.
A adoção da Modelagem Matemática, como uma alternativa Metodológica para o ensino da Matemática, pretende contribuir para que gradativamente se vá superando o tratamento estanque e compartimentalizado que tem caracterizado o seu ensino, pois, na aplicação dessa metodologia, um conteúdo matemático pode se repetir várias vezes no transcorrer dos 6 conjunto das atividades em momentos e situações distintas (BURAK, 2010, p.4).
Burak ressalta, porém, que essa proposta não se coloca como uma concepção fechada, mas que indica possibilidades de expansão nas discussões sobre a natureza da Educação Matemática, considerando-a como Ciência Humana e Social. Nesse sentido, mais tarde Burak e Klüber (2013, p. 35) afirmam que essa perspectiva de Educação Matemática:
Na Figura 1, temos o esquema de modelagem matemática. Nesse esquema temos algumas etapas do processo de modelagem, que devem ser seguidas, como a observação de uma situação – problema, a matematização, o modelo matemático e a validação. Essa última etapa é onde o aluno irá compreender as aplicações dos conteúdos no seu cotidiano. Assim, nessa metodologia os alunos participam da construção dos conteúdos estudados.
Figura 1 – Esquema de modelagem matemática
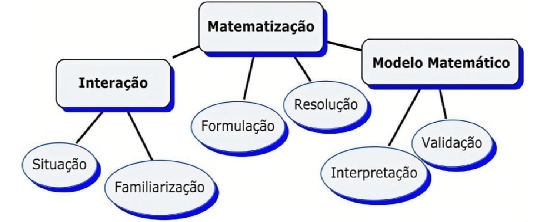
FONTE: BIEMBERNGUT (1999).
Biembengut (2019) diz que no ensino de matemática ou das ciências, por exemplo, não basta apresentar a ideia embutida no conceito (matemático, biológico, físico, químico, geográfico, histórico). Muitos desses conceitos necessitam ser contextualizados para a criança, seja por meio de atividades experimentais, seja por documentários, vídeos, entre outras formas.
E as artes manuais contribuem para o estímulo do talento criativo.
A modelagem matemática é um processo que proporciona ao aluno uma análise global da realidade que ele vivencia. É uma estratégia de ação que dá abertura ao aluno para pensar, criar e estabelecer relações, tendo liberdade para procurar suas próprias alternativas de solução, desenvolvendo atitudes positivas pela aprendizagem da matemática. (SILVA, 2007, p. 25).
Assim, destaca-se que esse interesse pode ser tanto num sentido positivo, como elementos ou fatos que são benéficos, vantagens ou sensações agradáveis quanto, num sentido negativo, como questões que trazem inquietação, transtorno e levam ao desejo de resolvê-las (BURAK, 2010).
2.1 MAQUETE E MODELO ARQUITETÔNICO
Observa-se que os alunos têm deficiência quando há algo referido a visão tridimensional, tal deficiência pode ocorrer pela forma que são abordados os conceitos geométricos, pois a visão espacial é uma habilidade desenvolvida individualmente, que pode ser construída usando percepção e experiência.
Em geral, as maquetes e os modelos arquitetônicos são uma representação do real em escala reduzida, o que pode apresentar para o aluno, uma aplicação dos conteúdos estudados, facilitando o entendimento através da prática.
Para reduzir essas deficiências, o professor pode trabalhar a construção de maquetes físicas. Na Figura 2, apresentamos modelos arquitetônicos tridimensionais. Podemos observar os espaços e fazer comparações com o ambiente real.
Figura 2 – Modelo arquitetônico tridimensional
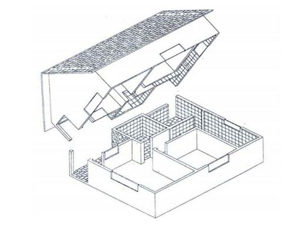
FONTE: FERREIRA (2004, p.06;22)
Para a confecção de maquetes é necessária a confecção da planta baixa. Na Figura 3, temos uma visão de uma planta baixa, ou seja, uma visão bidimensional onde podemos observar os formatos dos ambientes e os ângulos. Assim, conforme Felcher, Dias e Bierhalz (2015), maquetes podem ser utilizadas em qualquer nível de ensino, pois é uma ferramenta interdisciplinar que facilita a compreensão dos espaços e formas, beneficiando todos os envolvidos nessa metodologia.
Figura 3 – Visão da planta baixa
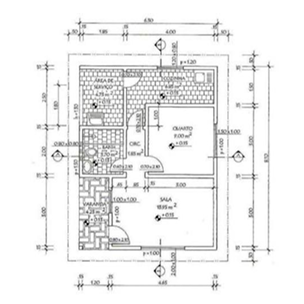
FONTE: FERREIRA (2004, p.06 e 22)
A Geometria envolve o estudo de um amplo conjunto de conceitos e procedimentos necessários para resolver problemas do mundo físico e de diferentes áreas do conhecimento. Assim, nesta unidade temática, estudar posição e deslocamentos no espaço, formas e relações entre elementos de figuras planas e espaciais pode desenvolver o pensamento geométrico dos alunos. Esse pensamento é necessário para investigar propriedades, fazer conjecturas e produzir argumentos geométricos convincentes. É importante, também, considerar o aspecto funcional que deve estar presente no estudo da Geometria: as transformações geométricas, sobretudo as simetrias. As ideias matemáticas fundamentais associadas a essa temática são, principalmente, construção, representação e interdependência. (BRAIL,2017, p,271).
Assim, a confecção de maquetes possibilita uma melhor aprendizagem dos conceitos geométricos, pois segundo a Base Nacional Comum Curricular (BNCC), no Ensino Fundamental – Anos Iniciais, espera-se que os alunos identifiquem e estabeleçam pontos de referência para a localização e o deslocamento de objetos, construindo representações de espaços conhecidos e estimem distâncias.
2.2 APRENDIZAGEM SIGNIFICATIVA
A aprendizagem é significativa quando faz realmente sentido para os alunos, se eles puderem internalizar esse novo material, explicando-o com suas próprias palavras e resolver, de forma satisfatória, novas situações que usam o material já aprendido como premissa. Já a aprendizagem mecânica é aquela em que o aluno aprende a partir de repetições, isto é, o estudante é passivo e de forma tradicional.
As aprendizagens que os alunos realizam na escola serão significativas à medida que conseguirem estabelecer relações substantivas e não arbitrárias entre os conteúdos escolares e os conhecimentos previamente construídos por eles, num processo de articulação de novos significados (BRASIL, 1997, p.38).
O conhecimento anterior sobre medidas de comprimento, unidades de medida de comprimento, figuras planas, entre outros, facilitarão a construção do conceito de “perímetro e área”. Assim, se os educandos participarem de forma ativa da construção do conhecimento, eles podem ter uma aprendizagem significativa. Diferente das metodologias tradicionais onde o aluno, em sua maioria das vezes, tem aprendizagem mecânica.
Conforme os PCN’s (1997), a aprendizagem significativa implica sempre em alguma ousadia: diante do problema posto, o aluno precisa elaborar hipóteses e experimentá-las. Fatores e processos afetivos, motivacionais e relacionais são importantes nesse momento. Os conhecimentos gerados na história pessoal e educativa têm um papel determinante na expectativa que o aluno tem da escola, do professor e de si, nas suas motivações e interesses, em seu autoconceito e em sua autoestima (BRASIL, 1997, p.38).
Diante do exposto, modelagem matemática no ambiente escolar, através da confecção de maquetes, pode sim ser uma ferramenta motivadora, favorecendo uma aprendizagem significativa para o educando, pois ele participa de forma ativa da construção do seu próprio conhecimento, ou seja, esse mecanismo de intervenção educativa ajuda no processo de construção de significados realizados pelos alunos no decorrer das atividades escolares de ensino e aprendizagem.
Os PCN’s esclarecem que o raciocínio no conteúdo de proporcionalidade deve envolver a exploração de situações de aprendizagem, as quais conduzem o discente a: “observar a variação entre grandezas, estabelecendo relação entre elas e construir estratégias de solução para resolver situações que envolvam a proporcionalidade” (BRASIL, 1998, p. 65).
Para que uma aprendizagem significativa possa acontecer, é necessária a disponibilidade para o envolvimento do aluno na aprendizagem, o empenho em estabelecer relações entre o que já sabe e o que está aprendendo, em usar os instrumentos adequados que conhece e dispõe para alcançar a maior compreensão possível. Essa aprendizagem exige uma ousadia para se colocar problemas, buscar soluções e experimentar novos caminhos, de maneira totalmente diferente da aprendizagem mecânica, na qual o aluno limita seu esforço apenas em memorizar ou estabelecer relações diretas e superficiais (BRASIL, 1997, p. 64).
Além disso, D’Ambrósio (1997) diz que a abordagem pedagógica começou com atividades concretas para que o aluno construísse seus próprios conceitos, por meio de atividades práticas para depois aplicar os conceitos teóricos como eles são e, consequentemente, convencê-lo de que estes são verdadeiros. É muito mais fácil para os indivíduos caracterizarem um objeto particular que enfatiza ser apresentado, tornando assim a sua aprendizagem significativa.
Buscamos uma matemática que se transforme num instrumento através do qual o homem possa criar uma relação racional com o seu meio, estabelecendo, dessa forma, uma consciência real do mundo. A consciência do possível na Educação Matemática hoje deve ter como meta o homem, como módulo a sociedade e como argumento a realidade (SOUZA, 1992, p. 75).
Deste modo, observamos que a prática e o manuseio dos materiais no ensino de matemática ficam claro que relacionar novos conceitos às informações já conhecidas pelos alunos é um caminho viável para obtenção de uma aprendizagem de fato efetiva e cheia de significado. Conforme cita Brasil (2000, p. 29):
2.3 ALGUMAS EXPERIÊNCIAS EXITOSAS
Quando tratamos de modelagem matemática (MM), no âmbito da educação, temos a certeza de que existem várias pesquisas que tratam do assunto. Assim, logo abaixo vamos tratar sobre alguns relatos de experiências exitosas.
2.3.1 O cálculo do raio da terra
Soares (2013), descreve que atividades extraclasse e experimentais são de suma importância para formação dos discentes em todos os níveis de ensino, pois proporciona que os conteúdos abordados em sala se consolidem com atividades praticadas num ambiente diferente. Também desperta o interesse motivando os participantes assim como a MM em sala de aula.
Fez uma atividade extraclasse e experimental com os discentes do curso de licenciatura plena em matemática, a referida atividade foi o cálculo do raio da terra onde os alunos tiveram o contato com a aplicação e prática de alguns conteúdos, a atividade foi executada à beira-mar, pois neste local pode ser visto a linha do horizonte e com o auxílio de um teodolito foi feito o experimento e aplicação.
Ainda ressalta que os relatos dos alunos que participaram da atividade extraclasse destacam que a aula prática contribuiu de forma significativa em sua formação acadêmica, pois se verificou com o experimento o que se conhecia apenas na teoria, assim, ficou evidenciado que teoria e prática é essencial no processo ensino-aprendizagem.
2.3.2 modelagens matemática como proposta de ensino de matemática no curso técnico integrado em agropecuária
Ainda ressalta que os relatos dos alunos que participaram da atividade extraclasse destacam que a aula prática contribuiu de forma significativa em sua formação acadêmica, pois se verificou com o experimento o que se conhecia apenas na teoria, assim, ficou evidenciado que teoria e prática é essencial no processo ensino-aprendizagem.
Lima (2018) diz que a modelagem matemática e a aplicação destes conhecimentos, na prática, possibilitaram um ambiente propício ao desenvolvimento de fatores cognitivos do aluno, como percepção, memória e raciocínio, para a prática realizada numa esfera interdisciplinar contribuiu de forma significativa para o ensino.
Dessa forma, foi desenvolvida a pesquisa intitulada de modelagem matemática como proposta de ensino de matemática no curso técnico integrado em agropecuária. Nessa pesquisa foram feitas atividades práticas aplicadas ao cotidiano relacionado ao curso em questão, como, por exemplo, quando se fala em dimensionar uma certa área para cultivo. No referido trabalho, a área dimensionada era 90 m² para o cultivo de milho, soja, sorgo e milheto.
Aplicando os conceitos de MM usando os conteúdos de números racionais, fração, porcentagem e regra de três, além de uma atividade de campo com a construção dos 90 m² para simular os problemas propostos e por fim, conclui-se que a atividade realizada é de suma importância para a vida profissional do futuro técnico.
2.3.3 Modelagem matemática no ensino de trigonometria
Segundo Alves (2017), a MM como ferramenta de ensino constrói novos saberes, sem definições decoradas e atividades quase mecânicas desvinculadas de aplicações, ainda frisa que a principal motivação dos professores está em ver os entusiasmos de seus alunos e a troca de experiências e assimilação das aulas ao participar desta metodologia, quebrando o paradigma do tradicional ensino de matemática. Assim, podemos motivar os alunos, mostrando onde se encontra a Matemática no cotidiano deles.
Nesta pesquisa sobre modelagem matemática no ensino de trigonometria, propõem que seja calculada a altura de uma árvore como atividade prática. Para isso é medido a altura do observador e a distância entre o mesmo e a árvore e com o auxílio de um teodolito artesanal pode ser calculado a altura desejada.
2.3.4 Modelagem matemática no ensino fundamental
Nessa perspectiva, Roque (2009) diz:
A Modelagem Matemática implica em um conjunto de saberes que faz parte de um novo paradigma educacional, que relaciona a aprendizagem dos alunos com fatos reais, onde possam levantar problemas identificados por eles e buscarem soluções que satisfaçam as condições iniciais que foram problematizadas. (ROQUE 2009).
Assim, para Roque (2009) o uso de MM como estratégia de ensino com alunos do Ensino Fundamental se mostrou interessante no sentido de que possibilita um olhar diferenciado sobre os conteúdos matemáticos. Um olhar que permite observar fenômenos reais sendo desvendados ou esclarecidos por conhecimento matemático, favorecendo o processo de ensino aprendizagem dos alunos.
Foi feito uma atividade prática interdisciplinar usando modelagem matemática, a referida atividade trata dos conteúdos de razão, proporção, regra de três e porcentagem onde é feito uma comparação dos pesos dos alunos com o peso de sua mochila, assim, os alunos conseguem verificar na prática esses conteúdos.
2.3.5 Modelagem matemática: Um trabalho com embalagens
Segundo Corrêa e Estephan (2008), a Modelagem Matemática, como estratégia de ensino, se mostra um caminho muito promissor na busca de um ensino eficaz, capaz de envolver o aluno, aproximando a Matemática descontextualizada da realidade, tornando a matemática de sala de aula mais atrativa.
Nessa pesquisa, são descritas oito atividades, sendo que a primeira era “analisando tipo e formas de embalagens”. Nessa atividade, os alunos ao observarem as embalagens teriam que diferenciar entre prisma, pirâmides e corpos redondos. A segunda e terceira atividades, denominadas “Identificando faces, arestas e vértices” e “Relação Euller”, nessa respectiva ordem, os alunos usavam as embalagens para descrever que sólido aquela embalagem representava, contar o número de vértices, faces e arestas de cada um. Já outra atividade foi utilizar sólidos construídos com canudos para aplicar a relação de Euller.
Na quarta, quinta e sexta atividades foram feitos trabalhos com caixas, sendo que na primeira dessas atividades foi a “Construção de um modelo para a caixinha de leite longa vida”, onde os alunos de posse das medidas da largura, comprimento e altura de uma caixa de leite calculavam a área total e o volume. Seguindo a ordem, a outra atividade nomeada de “Construção de um modelo cilíndrico para a caixinha de leite longa vida” essa atividade foi dividida em duas etapas.
Na primeira etapa, foi desenvolvida uma atividade prática para que os alunos tivessem uma aprendizagem sobre a área e o comprimento do círculo; já na segunda, os alunos poderiam trabalhar com embalagens cilíndricas. No entanto, na sexta atividade classificada de “Construção de uma caixinha aberta”, cada grupo recebeu uma folha de papel sulfite A4 para construção de uma caixinha aberta e depois calcular área e volume da caixinha.
A sétima atividade, chamada de “embalagem ótima”, foi proposto aos alunos que descobrissem a altura da embalagem ótima, para isso foi usado uma folha quadrada de 10 cm de lado, assim, cada equipe deveria descobrir a equação do volume em função da altura.
E por fim, a oitava atividade “Análise da mudança de embalagem de sabão em pó”, nessa atividade foi feito uma pesquisa sobre as dimensões das embalagens antigas e atuais de sabão em pó. Assim, de posse das medidas comprimento, altura e largura, foi feito o cálculo da área e do volume das respectivas embalagens. Deste modo, usando embalagens para se trabalhar conteúdos de geometria espacial com alunos do 3º ano do ensino médio, a pesquisa foi desenvolvida.
3 METODOLOGIA E ANÁLISE DOS DADOS
Neste capítulo, será apresentada a metodologia utilizada na pesquisa. Isto é, são apresentados os meios e as técnicas utilizadas para atingir os objetivos declarados. Inicialmente, será feita a caracterização da pesquisa quanto à sua natureza, abordagem e tratamento das informações. Esta etapa é necessária para investigar adequadamente o problema e estruturar adequadamente do processo investigatório.
3.1 CARACTERIZAÇÃO DA PESQUISA
De acordo com Fontelles (2009), a pesquisa científica é a aplicação prática de um conjunto de procedimentos cujo objetivo é produzir conhecimentos científicos para aplicação prática voltada para a solução de problemas concretos, específicos da vida moderna a fim de produzir um novo conhecimento, além de integrá-lo àqueles pré-existentes.
Do ponto de vista técnico, a pesquisa é de abordagem qualitativa e quantitativa de natureza aplicada. Fonseca (2002, p. 20) descreve que a pesquisa quantitativa recorre à linguagem matemática para descrever as causas de um fenômeno, as relações entre variáveis. A utilização conjunta da pesquisa qualitativa e quantitativa permite recolher mais informações do que se poderia conseguir isoladamente.
Para Silva (2010), a abordagem qualitativa trabalha com valores, crenças, representações, hábitos, atitudes e opiniões. Assim, nesta abordagem o pesquisador participa, observando e analisando os dados. Já na pesquisa quantitativa será feito um levantamento estatístico dos dados obtidos e aplicada após uma intervenção didática.
3.2 LOCAL E PARTICIPANTES DA PESQUISA
A pesquisa foi desenvolvida no período compreendido entre os meses de outubro e dezembro do ano de 2022, com estudantes do 7° ano do ensino fundamental da Escola Municipal Jornalista João Emílio Falcão, que está localizada na Rua Francisco Sousa Araújo, Número 4085, Residencial Vamos Ver o Sol, bairro Parque sul, na Cidade de Teresina-PI.
O estudo foi realizado com alunos de duas turmas, 7° ano “A” e 7° ano “B”, totalizando 24 participantes, onde eles fizeram dois testes: o teste inicial e o teste final. Cada um dos testes contendo 10 questões, sendo 5 questões de perímetro e 5 questões de área.
3.3 TÉCNICAS / INSTRUMENTOS DE COLETA DE DADOS PRIMEIRO ENCONTRO
Foi aplicado o teste inicial. O referido teste se faz necessário para avaliar os conhecimentos prévios dos alunos, que é o objetivo desse encontro. Após o teste, foi feita a divisão dos 24 alunos participantes, em três grupos de oito componentes para, assim, iniciar o desenvolvimento do trabalho.
Figura 4 – Aplicação do teste inicial

Fonte: O autor (2022).
SEGUNDO E TERCEIRO ENCONTRO
Conversamos com os alunos sobre os resultados obtidos no teste inicial. Assim, no segundo encontro, o objetivo era atribuir tarefas para cada um dos três grupos divididos no encontro anterior. Um grupo iria fazer as medições das repartições escolares, primeiro, segundo e terceiro bloco de salas; já os outros grupos para a quadra, quadra de areia e pátio. Já no terceiro encontro, continuamos com as medições dos ambientes da escola.
Percebemos que as salas de aulas eram padronizadas, o que facilitou o trabalho.
Figura 5 – Medidas das repartições da escola

Fonte: O autor (2022)
QUARTO ENCONTRO
Nesse encontro, como cada grupo já estava de posse das medidas colhidas, foi solicitado que cada grupo calculasse a área e o perímetro das salas, pátio, quadra de esportes e quadra de areia. Após isso, questionei aos alunos se eles tinham conseguido efetuar esses cálculos que os fora solicitado; as respostas foram bem satisfatórias.
Figura 6 – Área e perímetro da quadra de esportes

Fonte O autor (2022)
Figura 7 – Área e perímetro da sala de aula

Fonte: O autor (2022)
Figura 8 – Trapézio

Fonte: O autor (2022)
Figura 9 – Área do trapézio por decomposição

Fonte: O autor (2022)
Figura 10 – Área do trapézio
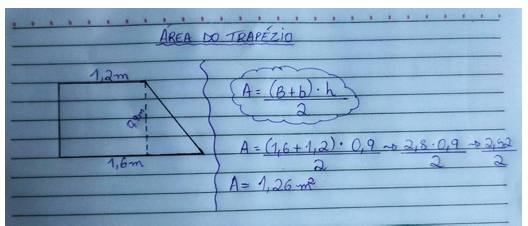
Fonte: O autor (2022)
Figura 11 – Resultado da área e perímetro das salas de aula
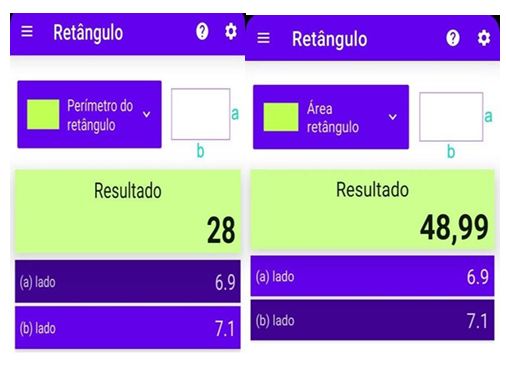
Fonte: O autor (2022)
Figura 12 – Resultado da área do trapézio Fonte: O autor (2022)
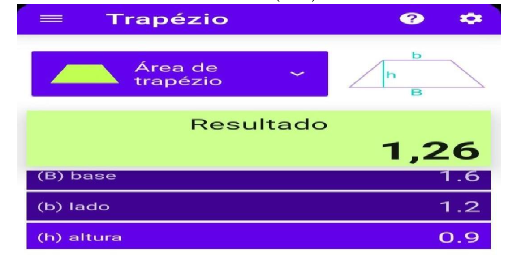
Fonte: O autor (2022)
SEXTO ENCONTRO
Foi dado início a confecção da planta baixa. Nesse momento, gerou uma dúvida: os alunos questionaram como iriam esquadrar, como saberiam se aquela reta estaria realmente reta. Então foi ensinado a eles como usar o esquadro e os mesmos perceberam que por dois pontos passa uma única reta.
Além disso, os alunos foram questionados como conseguimos transpor aquelas medidas para o papel. Teve alunos que responderam usando escala, porém não sabiam como usar. Então fui explicar um pouco sobre escala e alguns logo disseram: “quero usar a escala 1:100”, pois já perceberam que seria uma escala melhor para se trabalhar.
Resolvemos então usar três escalas: 1:100, 1:200 e 1:300; pois, assim, os alunos irão perceber a diferença entre as escalas e entender qual escala deixaria a imagem maior e qual deixaria a imagem menor, ou seja, de maneira intuitiva iriam ver a questão de ampliação e redução.
Figura 13 – Confecção da planta baixa da escola

Fonte: O autor (2022)
QUINTO ENCONTRO
Iniciamos este encontro usando o aplicativo “calculadora de área e perímetro” para validar os resultados obtidos no quarto encontro, o que favoreceu o aprendizado dos alunos, pois eles não tinham conhecimento do aplicativo; no entanto, foi dito a eles que o aplicativo é só uma maneira que temos de validar os dados obtidos, então o mais importante é que eles mesmos aprendam a fazer esses cálculos.
Figura 14 – Resultado da área e perímetro da quadra de esportes
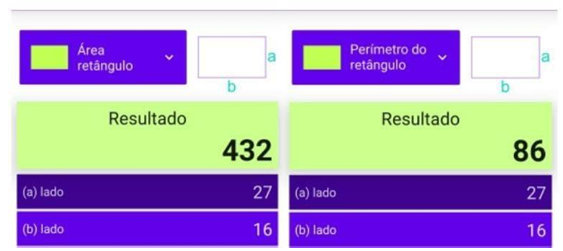
Fonte: O autor (2022)
Figura 15 – Planta baixa da escola
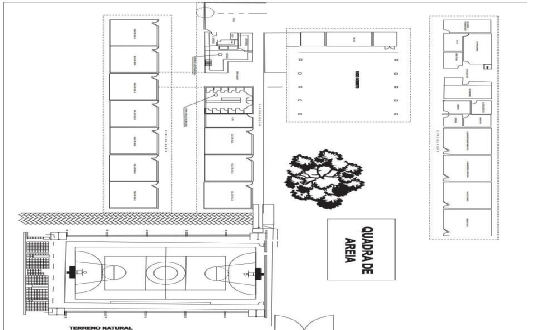
Fonte: O autor (2022)
SÉTIMO ENCONTRO
Nesse encontro, continuamos com a confecção da planta baixa. Em pouco tempo, os alunos já perceberam as diferenças entre as escalas e, o grupo com a escala 1:100 disse: “A minha planta vai ficar grande”, sendo que tiveram que unir dois papéis madeira. Já o grupo com escala 1:200 disse: “a minha planta, acho que vai ficar em um tamanho legal”, e por fim, o grupo na escala 1:300 disse que o deles iria ficar pequeno.
Assim, questionei quais as diferenças entre essas escalas e logo percebi que eles haviam entendido, o que me deixou bastante satisfeito, sem contar com as palavras da gestão escolar que havia dito que nunca tinha visto uma aula de matemática daquele jeito, onde os alunos participavam daquela forma e que muitas vezes para encerrar a aula tinha-se que ir chamar os alunos.
OITAVO E NONO ENCONTRO
Iniciamos o oitavo encontro com a confecção da maquete. Nessa etapa, importante seria a visão tridimensional dos alunos, essa foi a etapa mais aguardada por eles, pois sempre estavam perguntando-me quando iriam construir a maquete. Já no nono encontro, continuamos a montagem da maquete, montando as repartições da escola.
Figura 16 – Confecção da

Fonte: O autor (2022)
Figura 17 – Montagem da maquete

Fonte: O autor (2022)
Figura 18 – Um bloco de salas

Fonte: O autor (2022)
DÉCIMO ENCONTRO
Nesse encontro, foi feita a pintura e conclusão das maquetes. Nessa etapa, podemos destacar a participação dos alunos e o estímulo do trabalho em grupo, assim como o desenvolvimento de habilidades como concentração e coordenação motora.
Figura 19 – Maquete

Fonte: O autor (2022)
Figura 20 – Maquetes concluídas

Fonte: O autor (2022))
DÉCIMO PRIMEIRO ENCONTRO
Nesse encontro, foi aplicado o teste final, contendo 10 questões. Assim como o teste inicial, 5 questões de perímetro e 5 questões de área. O teste final se faz necessário para a comparação dos resultados com o teste inicial.
Figura 21 – Aplicação do teste final

Fonte: O autor (2022)
4 RESULTADOS E DISCUSSÕES
Este capítulo tem por objetivo organizar e apresentar os dados coletados por meio da aplicação dos testes inicial e final na turma de 7° ano da Escola Municipal Jornalista João Emílio Falcão. Primeiramente, vamos apresentar o quadro 1, onde será destacado o que observei em alguns encontros realizados na aplicação da atividade. Em seguida, apresentaremos três Tabelas: a primeira, com os alunos e suas respectivas notas. Em seguida, outra tabela com a frequência de notas do teste inicial e a terceira tabela, que mostra o número total de acertos e erros do primeiro teste.
Depois, na tentativa de melhor ilustrar os resultados, foi apresentado o Gráfico 1 de colunas, demonstrando o total de acertos e erros do teste inicial. Logo após, nas tabelas 4,5 e 6, estão apresentadas as notas dos alunos, a frequência de notas e total de acertos e erros do teste final, seguindo a respectiva ordem. Em seguida, o gráfico 2 ilustra o total de acertos e erros do teste final. Por fim, a comparação das médias dos dois testes foi apresentada na tabela 7 e no Gráfico 3.
Quadro 1 – Observações nos encontros
ENCONTROS OBSERVAÇÕES Primeiro, Segundo e terceiro No primeiro encontro, os alunos estavam muitoansiosos para o início da atividade, assim, foi aplicado o teste inicial. Após a aplicação do teste inicial, no primeiro encontro, iniciamos a aplicação da atividade com o segundo e terceiro encontro, onde os alunos fizeram as medições da escola. Nessa etapa, percebi que algumas dificuldades que os alunos tinham em relação às conversões entre as unidades de medidas já não existiam, principalmente em relação a centímetro e metro. Quarto e quinto Continuamos com o quarto e quinto encontro, onde os alunos calcularam o perímetro e a área de algumas repartições da escola e depois com o uso de um aplicativo, foi feito a validação dos resultados, respectivamente nessa ordem. Nessas duas etapas percebi que os alunos obtiveram o conhecimento de perímetro e área. Na prática, conseguindo efetuar os cálculos que lhes foram propostos. Sexto e sétimo Nesses respectivos encontros, os alunos tiveram o contato com o conteúdo de razão onde os mesmos através da prática rapidamente conseguiram notar as diferenças entre as escalas e as questões de ampliação e redução. Oitavo , nono e décimo Foi observado, através do uso e manuseio de materiais manipuláveis, o desenvolvimento da visão tridimensional, concentração, coordenação motora e o raciocínio lógico dos alunos. Décimo primeiro Encerramos a atividade com a aplicação do testefinal, onde pude perceber que os alunos obtiveram êxito na resolução das questões.
Fonte: Elaboração própria (2022)
A aprendizagem da Matemática depende de uma grande variedade de fatores o que torna o seu ensino bastante complexo. É necessário desenvolver o raciocínio lógico e estimular o pensamento independente, a criatividade e a capacidade de resolver problemas. Desta forma, os professores de matemática devem concentrar-se em aumentar a motivação para a aprendizagem, desenvolver a autoconfiança, organização, concentração, atenção, raciocínio lógico-dedutivo e sentido cooperativo, aumentando a socialização e as interações pessoais. (MOURA, 2006, p. 73).
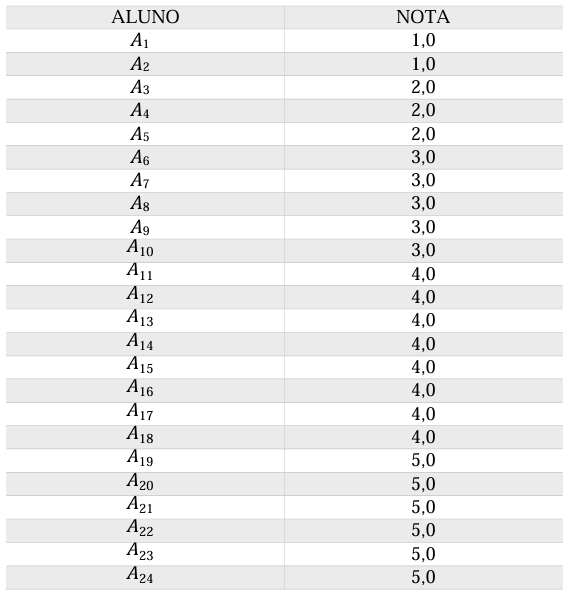
A Tabela 1 mostra os alunos e suas respectivas notas organizadas em ordem crescente. É importante enfatizar que os alunos estão representados por letras que diferem em índices, com o objetivo de preservar suas identidades.
Podemos observar, conforme os dados expostos na Tabela 1, que tivemos 8,33% dos alunos que tiraram nota 1; 12,5% tiraram nota 2; os que tiraram nota 3 foram 20,84%; os que conseguiram tirar 4 e 5 representam 33,33% e 25%, respectivamente.
Tabela 1 – Resultado do teste inicial na escala de 0 a 10 pontos
Fonte: Elaboração própria (2022)
O resultado apresentado mostra um desempenho abaixo do que esperamos para alunos nesse ano escolar, o fato pode estar relacionado à forma como os conteúdos matemáticos vêm sendo abordados nessa turma.
Um dado importante é que nenhum aluno tirou nota zero, entretanto, como já foi observado, apenas 25% dos estudantes conseguiram atingir nota 5, que foi a maior nota do exame e que está abaixo da média de aprovação da escola que é de 6.
A seguir, a Tabela 2, ilustra a frequência absoluta e a frequência relativa das notas do teste inicial. A tabela apresenta uma organização nas informações coletadas no teste inicial, por meio das frequências absoluta e relativa, exposições desse tipo objetivam tornar mais clara a real situação em que se encontra o nível de conhecimento matemático que a turma apresentou de conforme as respostas coletadas no teste inicial
Tabela 2 – Frequência de notas do teste inicial
NOTAS FREQUÊNCIAABSOLUTA FREQUÊNCIARELATIVA 1 2 8,33% 2 3 12,5% 3 5 20,84% 4 8 33,33% 5 6 25% TOTAL 24 100%
Fonte: elaboração própria (2022)
A tabela 3 mostra os resultados obtidos no teste inicial. Nesse resultado podemos observar o número de acertos e erros dos alunos, o que nos dá uma ideia dos conhecimentos prévios desses alunos sobre esses conteúdos abordados, pois, para Moreira (2006) os conhecimentos prévios dos alunos são importantes para a aprendizagem, e cabe ao professor considerá-los, encontrando estratégias para inseri-los em sua prática pedagógica. Assim, para que a aprendizagem aconteça, é necessário que as ideias tenham uma relação com os conhecimentos prévios do estudante, de modo que consiga relacionar com suas vivências.
Tabela 3 – Acertos e erros do teste inicial
Questões Acertos Erros 1 5 19 2 12 12 3 13 11 4 06 18 5 11 13 6 05 19 7 13 11 8 06 18 9 07 17 10 07 17
Fonte: elaboração própria (2022)
Os resultados apresentados na tabela 3 nos mostram os conhecimentos dos alunos antes do desenvolvimento do trabalho, por meio dos dados exibidos na tabela podemos perceber que são altas as quantidades de erros apresentados por questão na referida turma; apenas nas questões 3 e 7 houve menor quantidade de erros do que acerto, este fato pode demonstrar indícios de que a aprendizagem matemática dos alunos está relacionada ao modo como os professores vêm desenvolvendo suas metodologias.
Na tentativa de melhorar a visualização e compreensão da situação apresentada pela turma, depois da aplicação do teste inicial, consequentemente antes do início do desenvolvimento da pesquisa e aplicação da metodologia de ensino de matemática por meio de modelagem, os resultados se encontram exibidos no gráfico 1, e serão melhor discutidos abaixo.
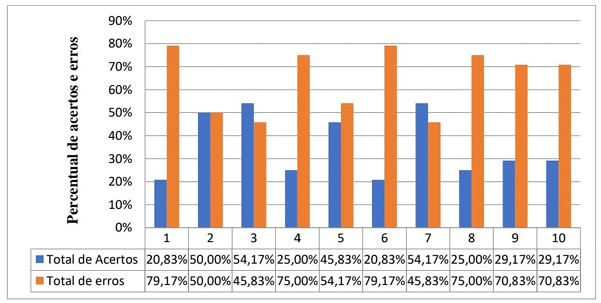
Gráfico 1 – Acertos e erros do teste inicial
Fonte: elaboração própria (2022)
O gráfico 1 apresenta os resultados percentuais de todos os acertos e erros de todas as questões do pré-teste. Considerando que os 24 alunos da turma fizeram o teste que continha 10 questões, então para cada quantidade de acertos e erros obtidos em todas as questões existia 240 possibilidades para acertos e erros para a turma em questão.
Dessa maneira, podemos ter uma visão geral do desempenho da turma, uma vez que já foram observadas na Tabela 3, e foi possível verificar que houve uma variação momentânea de melhores desempenhos, de questão para questão, porém em quase todas as questões a quantidade de erros foi superior à quantidade de acertos.
Pelos resultados exibidos no gráfico acima, podemos verificar os percentuais de acertos e erros questão por questão. A questão de número 1, apresenta 20,83% de acertos e 79,17% de erros; já a questão de números 2 ficou bem dividida com 50%, tanto para acerto quanto para erros. É importante enfatizar que as duas primeiras questões requerem que os alunos tivessem conhecimento do cálculo do perímetro de figuras planas para respondê-las. A terceira questão foi uma das duas questões em que a quantidade de acertos foi superior à quantidade de erros neste primeiro teste, sendo 54,17% de acertos e 45,83% de erros. A referida questão exigia além do cálculo do perímetro que os alunos utilizassem conhecimento de matemática financeira, frequentemente utilizada em nosso dia a dia.
Nas questões 4 e 5, também foram solicitados o conhecimento do cálculo de perímetro, só que agora exigia-se um pouco de atenção, pois além de seguir ordem respectiva na questão quatro, a questão cinco apresentou a ideia de comparação de tamanhos de perímetros, visando verificar se os alunos tinham o conhecimento do que significa dobro, triplo e quádruplo em termos de redução e ampliação. Nestas questões, a quantidade de acertos foi inferior à de erros, com 25% e 75% para acertos e erros, respectivamente para quarta questão e 45,83% e 54,17%, para quinta questão.
Nas questões 6 e 7 foram requeridos dos alunos os conhecimentos dos cálculos de áreas de figuras geométricas planas, e apenas 20,83% dos alunos acertaram a questão 6, ao tempo que 79,17% erraram a questão. Já a questão de número 7, a exemplo da terceira questão, foi outra em que a quantidade de acertos foi superior a de erros, e apesar da questão 3 exigir conhecimentos de cálculo de perímetro e a questão 7 de área, coincidentemente, os percentuais foram exatamente iguais para acertos e erros, ou seja, 54,17% e 45,83%, nessa ordem.
A questão de número 8 apresenta o uso da matemática nas construções e solicita que os alunos calculem a quantidade de telhas necessárias para cobrir uma casa, sendo conhecida a quantidade de telhas por metros quadrados e as medidas de comprimento e largura do telhado. O resultado apresentado para essa questão foi 25% de acertos e 75% de erros. Já as questões 9 e 10 são teoricamente mais simples que a questão 8, pois em ambas é necessário o conhecimento dos cálculos de área de figuras planas para responder. Vale ressaltar que a questão 9 trata de triângulos retângulos e a 10, de retângulo, o que torna a questão ligeiramente mais simples, mas curiosamente os percentuais de acertos e erros foram 29,17% e 70,83% para acertos e erros, respectivamente, em ambas as questões.
De modo geral, percebemos que o desempenho da turma foi abaixo do esperado para uma turma de ensino fundamental de 7° ano, quando são exigidos que eles utilizem conhecimentos de geometria plana para os cálculos de perímetros e áreas de figuras planas com ou sem o uso de malhas quadriculadas. Este fato pode ser consequência da abordagem didática, usando os métodos tradicionais de ensino ou de uma soma de fatores que vem tornando o ensino de matemática cada vez mais fragilizado.
Dessa forma, devemos desenvolver meios que favoreçam um ambiente propício ao desenvolvimento matemático de todos os estudantes. Abaixo, está exibida a média aritmética dos acertos da turma no teste inicial.
Média de acertos do teste inicial
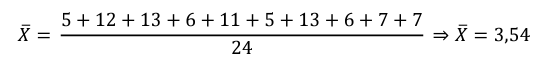
Ao analisar a média de acertos obtida no teste inicial, observamos que, em geral, os alunos estão abaixo de 50% de aproveitamento, ratificando que os conhecimentos prévios dos alunos referentes aos conteúdos abordados estão abaixo da média de aprovação adotada pela escola, que é 6. Ou seja, no teste inicial, 100% dos alunos estão abaixo da média. A tabela 4 mostra as notas dos alunos no teste final, organizadas em ordem crescente.
Tabela 4 – Resultado do teste final em uma escala de 0 a 10
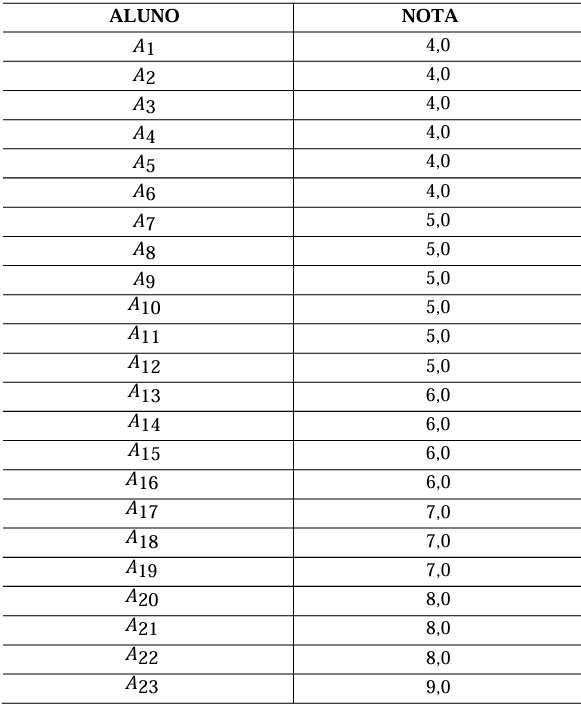

É possível perceber, conforme a tabela 4, que houve uma melhora no desempenho dos alunos quando comparamos com o teste inicial. A menor nota foi 4, e no teste inicial tivemos nota 1. No teste inicial, a maior nota foi 5, já no teste final, tivemos 9 como melhor nota.
Consoante os dados, depois do desenvolvimento do trabalho e aplicação da metodologia com uso da modelagem matemática no ambiente escolar, obtivemos que 25% dos alunos tiraram nota 4, outros 25% conseguiram tirar nota 5, e 50% da turma ficaram com notas maior ou igual a 6, sendo assim distribuídos 16,67% com notas 6; 12,5% com notas 7; outros 12,5% com 8 e por fim, 8,33% com nota 9. O resultado apresentado acima pode ser consequência da aplicação da metodologia diversificada para o ensino de matemática. A seguir, a tabela 5 ilustra a frequência absoluta e frequência relativa das notas do teste final.
Tabela 5 – Frequência de notas do teste final
NOTAS FREQUÊNCIA ABSOLUTA FREQUÊNCIA RELATIVA 04 06 25% 05 06 25% 06 04 16,67% 07 03 12,5% 08 03 12,5% 09 02 8,33% TOTAL 24 100%
Fonte: elaboração própria (2022)
A tabela acima apresenta uma organização das informações coletadas no teste final por meio das frequências absoluta e relativa, exposições desse tipo objetivam demonstrar o nível de conhecimento dos alunos agora após o desenvolvimento do trabalho, conforme as respostas coletadas no teste final. Vale ressaltar que na tabela 5 podemos observar que 50% dos alunos alcançaram a média de aprovação da escola, além disso, 50% obtiveram notas 4 ou 5 no teste, deixando claro que houve um avanço na aprendizagem dos alunos.
A tabela 6 mostra os resultados obtidos no exame. Segundo os dados, podemos observar o número de acertos e erros dos alunos, o que nos fornece uma ideia dos efeitos causados na aprendizagem matemática dos estudantes, em razão da metodologia desenvolvida.
Tabela 6 – Acertos e erros do teste final
Questões Acertos Erros 1 15 09 2 20 04 3 20 04 4 11 13 5 22 02 6 12 12 7 18 06 8 12 12 9 14 10 10 15 09
Fonte: elaboração própria (2022)
Os resultados apresentados na Tabela 6 nos mostram os conhecimentos dos alunos depois do desenvolvimento do trabalho. Através dos dados exibidos na Tabela podemos perceber uma considerável evolução no nível de desempenho da turma, pois as quantidades de erros apresentadas por questão na referida turma diminuíram significativamente.
Podemos observar que apenas uma questão tem quantidade de erros maior que a quantidade de acertos, outras duas questões têm quantidades de erros e acertos iguais. Nas demais, as quantidades de acertos superam os erros. Este fato talvez possa ser justificado pela metodologia aplicada nas aulas durante o desenvolvimento do projeto.
Na tentativa de melhorar a visualização e compreensão dos resultados da turma ilustrada pela tabela 6, depois da aplicação do teste final, consequentemente depois do desenvolvimento da pesquisa e aplicação da metodologia de ensino de matemática por meio de modelagem, os dados se encontram exibidos no gráfico 2, e serão melhor discutidos abaixo.
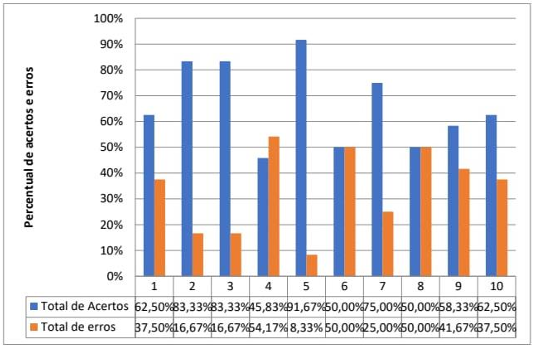
Gráfico 2 – Acertos e erros do teste final
Fonte: elaboração própria (2022)
O gráfico 2 apresenta os resultados percentuais de todos os acertos e erros de todas as questões do pós-teste. Considerando que os 24 alunos da turma fizeram o teste que continha 10 questões, então para cada quantidade de acertos e erros obtidos em todas as questões existiam 240 possibilidades para acertos e erros para a turma em questão, como foi relatado anteriormente nos comentários do gráfico 1.
Dessa forma, podemos ter uma visão geral se de fato a metodologia utilizada surtiu algum efeito positivo na aprendizagem dos alunos, uma vez que já foram observadas na tabela 6, e foi possível verificar que houve uma melhora significativa nos desempenhos, no momento das resoluções das questões.
Pelos resultados exibidos no gráfico acima, podemos verificar os percentuais de acertos e erros questão por questão, a exemplo do gráfico 1 para o teste inicial, a questão de número 1 representa 62,5 de acertos e 37,5% de erros, já a questão de números 2 ficou com 83,33% e 16,67% de acertos e erros na respectiva ordem. A exemplo do teste inicial, as questões 1 e 2 tratam de perímetros de figuras planas, o que aproxima os dois testes a fim de facilitar a comparação de desempenho dos estudantes. A terceira questão apresentou os mesmos percentuais da questão 2, e é mais uma em que requer dos alunos o conhecimento para o cálculo do perímetro, a exemplo da questão 3 do teste inicial.
As questões 4 e 5 do teste final também mantiveram relação de proximidade com as do pré-teste, uma vez que também solicitou aos alunos o conhecimento do cálculo de perímetro. Nestas questões, a quantidade de acertos e erros foram os seguintes: a questão 4 com 45,83% e 54,17% de acertos e erros, respectivamente, e a questão 5, com 91,67% de acertos e 8,33% de erros. É importante enfatizar que a quarta questão foi a única do teste final a ter mais erros do que acertos.
As questões 6 e 7 mantiveram a relação direta com as respectivas questões do teste inicial, pois foram requeridos dos alunos os conhecimentos de cálculos de áreas de figuras geométricas planas, e no que se refere à sexta questão, metade acertou a questão, em consequência a outra metade errou, uma vez que todos fizeram o teste. Já a questão de número 7, apresentou um grande avanço e 75% dos alunos obtiveram êxito na resolução da questão, outros 25% não conseguiram sucesso na referida questão.
Não diferente, as questões 8, 9 e 10 trataram de cálculos de áreas de figuras planas. Assim, as questões se mantiveram ligadas por ideias de resolução das respectivas questões do teste inicial, o que facilita a comparação de desempenho. A questão de número 8, a exemplo da questão 6, ficou com 50% para acertos e para erros, já os percentuais para as questões 9 e 10 mostraram uma boa evolução dos alunos, sendo 58,33% e 41,67% os percentuais de acertos e erros da questão 9 e 62,5% e 37,5%, os da questão de número 10.
A média aritmética dos acertos da turma após o desenvolvimento do trabalho e aplicação do teste final segue abaixo.
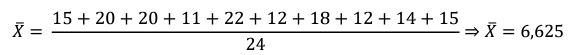
A tabela 7 apresenta, de forma organizada, as médias inicial e final. Pelo Gráfico 3 observamos que após a aplicação da sequência didática usando modelagem matemática, houve um crescimento de 3,085 na média obtida pelos alunos, onde eles alcançaram uma média geral de 6,625, ou seja, 0,625 acima da média de aprovação da escola.
Tabela 7 – Comparação das médias do teste inicial e do teste final
MÉDIAS TESTE INICIAL 3,54 TESTE FINAL 6,625
Fonte: elaboração própria (2022)
O gráfico 3 procura deixar os resultados da média mais evidente, por meio dele fica bem visível o crescimento da média no teste final em relação ao teste inicial.
Gráfico 3 – Comparação das médias do teste inicial e final
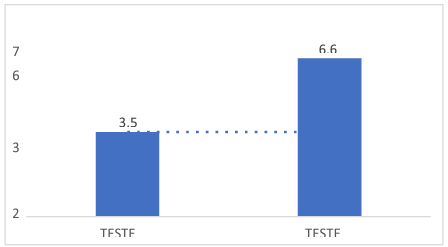
Fonte: elaboração própria (2022)
Tudo isso mostra que o desempenho da turma melhorou consideravelmente depois do desenvolvimento da prática pedagógica, pois houve uma melhora de pouco mais de 87% no desempenho dos alunos, segundo as médias apresentadas, mostrando assim que o objetivo foi alcançado, e que esta atividade é viável para o processo de ensino aprendizagem de matemática.
5 CONSIDERAÇÕES FINAIS
Ao se investigar e analisar metodologias de ensino em matemática descobre-se que, para proporcionar uma aprendizagem significativa com os alunos é necessário despertar o interesse deles pelos conteúdos abordados. Assim, os professores de matemática devem propor meios em que os alunos participem de forma ativa da abordagem metodológica, mostrando que a matemática pode ser contextualizada e prazerosa de se aprender.
Desta forma, ao realizar as atividades, propomos como objetivo geral verificar quais efeitos as intervenções educativas podem proporcionar aos estudantes do 7ºano no ensino de perímetro e área, utilizando modelagem matemática no ambiente escolar através da confecção de maquete.
Assim, ao analisar os resultados, fica claro que a Modelagem Matemática é uma estratégia no ensino de matemática viável, pois podemos observar a aprendizagem dos estudantes que participam. Ao mesmo tempo, percebi que os alunos estavam motivados durante todas as etapas, o que me deixou bastante entusiasmado e fez com que a atividade fosse prazerosa.
Almeida, Silva e Vertuan (ANO?) consideram que, ao utilizar MM como alternativa pedagógica, inserimos os alunos em um contexto de aprendizagem onde os mesmos participam de forma ativa, o que os leva a pensar sobre os objetivos matemáticos ali relacionados, além disso, os trabalhos em grupos são enriquecedores na prática de modelagem. Assim, quando exploramos uma prática pedagógica, por meio da Modelagem Matemática, nos deparamos com certezas de relatos de sucesso em sala de aula.
Desta forma, deixo claro que metodologias utilizando modelagem matemática podem melhorar os processos de ensino e aprendizagem dos alunos. Notamos, dessa forma, que ainda há muito a ser feito na educação, porém acredito que um dos causadores das dificuldades apresentadas são a grande quantidade de conteúdo que os professores são cobrados a trabalhar, alinhado com o pouco tempo em sala de aula.
REFERÊNCIAS
ALMEIDA, L. W. de; SILVA, K. P. da; VERTUAN, R. E. Modelagem Matemática na educação básica. 1ª ed. 1ª reimpressão. São Paulo: Contexto, 2013.
ALVES, modelagem matemática no ensino de trigonometria.2017.73f. Dissertação de Mestrado – Universidade Federal Do Maranhão , MA Disponível em: https://tedebc.ufma.br/jspui/bitstream/tede/1297/2/Gleyciane%20Araujo.pdf>. Acesso em:05/02/2023.
BASSANEZI, R. C. Modelagem matemática teoria e pratica. São Paulo, 2015.
Bassanezi, Rodney, C. “Modelagem como estratégia metodológica no ensino da matemática”. Boletim de Educação da SBMAC, São Paulo: IMECC/Unicamp.1994.
BASSANEZI, R. C. Ensino-aprendizagem com modelagem matemática: uma nova estratégia. 3.ed. São Paulo: Contexto, 2009.
BASSANEZI, R. C. Ensino-aprendizagem com modelagem matemática: uma nova estratégia. São Paulo: Contexto, 2002.
BRASIL. Secretaria de Educação Fundamental. Parâmetros curriculares nacionais: Matemática/ Secretaria de Educação Fundamental. Brasília: MEC/SEF, 1998.
BRASIL. Secretaria de Educação Fundamental. Parâmetros curriculares nacionais: introdução aos parâmetros curriculares nacionais / Secretaria de Educação Fundamental. – Brasília: MEC/SEF, 1997.
BRASIL. Ministério da Educação. Base Nacional Comum Curricular. Brasília, 2018. FERREIRA, P . Desenho arquitetônico. Rio de Janeiro: Ao livro técnico, 2004.
BIEMBENGUT,M. S.; HEIN, Modelagem Matemática no ensino. São Paulo: Contexto, 2018.
BIEMBENGUT,M. S., Modelagem nos anos iniciais do ensino fundamental. São Paulo: Contexto, 2018.
BURAK, D. Modelagem Matemática e a Sala de Aula. In: I EPMEM – Encontro Paranaense da Modelagem Na Educação Matemática. 2004, Londrina. Anais do I EPMEM, 2004.
BURAK, D. Modelagem Matemática sob um olhar de Educação Matemática e suas implicações para a construção do conhecimento matemático em sala de aula. Revista de Modelagem na Educação Matemática(FURB), v. 1, n. 1, p. 10-27, 2010.
BURAK, D.; KLÜBER, T. E. Considerações sobre modelagem matemática em uma perspectiva de Educação Matemática. Margens (UFPA), v. 6, p. 33-50, 2013.
CORRÊA, Roseni de Jesus; ESTEPHAN;Violrta Maria, Modelagem Matemática: Um Trabalho Com Embalagens. 2008.
D’AMBROSIO, U. Matemática, ensino e educação: uma proposta global. Temas &Debates: SBEM, São Paulo, ano IV. n. 3, p.1-15, 1991.
FELCHER, C. D. O.; DIAS, L. F.; BIERHALZ, C. D. K. Construindo Maquetes – Uma Estratégia Didática Interdisciplinar no Eixo Geometrias: Espaço e Forma. Revista Científica em Educação a Distância. V.5, No 2, 2015. Disponível em: . Acesso em: 05/12/22.
FONTELLES, R. G. S. et al. Metodologia da pesquisa cientifica: diretrizes para elaboração de um protocolo de pesquisa. Belém – Para, 2009.
GIL, A. C. Metodos e técnicas de pesquisa social. 4. ed. São Paulo: Atlas, 2002.
LIMA,H.A. Contribuições da Modelagem Matemática Como Proposta de Ensino de Matemática No Curso Técnico Integrado De Agropecuária. 2018.
MOREIRA, M.A. Aprendizagem significativa: a teoria de David Ausubel / Marco A. Moreira, Elcie F. Salzano Masini. São Paulo: Morais, 1982.
MOREIRA, Marco Antônio. Teorias de Aprendizagem. São Paulo: E.P.U., 2006.
MOURA, M. O. A séria busca no jogo: do lúdico na matemática. In: KISHIMOTO, T. M. (Org.). Jogo, brinquedo, brincadeira e a educação. 9. ed. São Paulo: Cortez, 2006.
ROQUE, Carla Cristina Escorsin. Modelagem Matemática no Ensino Fundamental. Revista da Gestão Escolar Paraná. Venceslau Braz: Revista da Gestão Escolar Paraná , 2009. Disponível em:< file:///C:/Users/USER/Downloads/artigo_carla_cristina_escorsin_roque.pdf> . Acesso em 05/02/2023
SILVA, G. C. R. F. O método na psicologia: abordagem qualitativa e quantitativa. Amazonas, 2010.
SOARES,R.A.L. Atividade Extraclasse: Cálculo do Raio da Terra. CONNEP 2013.
TRINDADE, D. F . Interdisciplinaridade: Um novo sobre as ciências. In Fazenda, I.(org). O que e interdisciplinaridade? . São Paulo: Cortez.
1Mestre em matemática /IFPI-PROFMAT. Email: caflo.2021114pmat08@aluno.ifpi.edu.br
2Mestre em matemática /IFPI-PROFMAT. Email: caflo.2021114pmat17@aluno.ifpi.edu.br
3Mestre em matemática /IFPI-PROFMAT. Email: caflo.2021114pmat01@aluno.ifpi.edu.br
4Metre professor do PROFMAT do IFPI de Floriano. Email: gildon@ifpi.edu.br
5Professor Dr. do PROFMAT do IFPI de Floriano. Email: robertoarruda@ifpi.edu.br
