REGISTRO DOI: 10.5281/zenodo.10509989
Laés de Castro Cavalcante;
Orientador: Prof. Me. Luan da Silva Santos
RESUMO
O presente trabalho tem como objetivo analisar as contribuições que o uso do GeoGebra pode trazer para o ensino-aprendizagem da trigonometria aos alunos do 2.º ano do ensino médio, focando no estudo das funções seno e cosseno. Avaliando se os alunos são capazes de resolverem problemas envolvendo as referidas funções por meio do manuseio do software, identificando os pontos positivos e negativos quanto a utilização do método. Para isso, foi desenvolvido um curso de dez horas aulas, ministradas em um laboratório de informática, na qual os estudantes foram instigados a realizarem o estudo das funções seno e cosseno, observando como é o comportamento gráfico conforme a variação dos seus parâmetros nas funções do tipo y = a . sen(b . x + c ) + d e y = a . cos(b . x + c) + d, interagindo em ambiente gráfico, podendo movimentar os parâmetros através de controles deslizantes, recursos presentes no software. As atividades foram desenvolvidas em uma turma do 2.º ano de informática do IFPI campus São Raimundo Nonato, sendo que estas foram planejadas e divididas em quatro etapas, de modo a alcançar um melhor resultado. No decorrer do curso, foi possível analisar como os alunos realizaram cada problema proposto, notando que a maioria conseguiram resolver sem muitas dificuldades. Também, através dos relatos dos discentes que se submeteram ao projeto, obtidos por meio de questionários, permitiu constatar que houve uma boa aceitação quanto a utilização do método.
PALAVRAS-CHAVE: Trigonometria. GeoGebra. Ensino.
ABSTRACT
The present work aims to analyze the contributions that the use of GeoGebra can bring to the teaching-learning of trigonometry for 2.º year high school students, focusing on the study of the sine and cosine functions. Assessing whether students are capable of solving problems involved in the aforementioned functions using the software, identifying the positive and negative points regarding the use of the method. For this, a ten-hour course was developed, taught in a computer laboratory, in which students were encouraged to study the sine and cosine functions, observing how the graphic behavior is according to the variation of their functions in the functions of the type y = a . sen(b . x + c ) + d e y = a . cos(b . x + c) + d, interacting in a graphical environment, being able to move the parameters through sliders, resources present in the software. The activities were developed in a 2.º year IT class at the IFPI campus São Raimundo Nonato, and were planned and divided into four stages, in order to achieve a better result. During the course, it was possible to analyze how the students performed each problem proposed, noting that the majority managed to solve them without many difficulties. Also, through the reports of the students who underwent the project, obtained through questionnaires, it was possible to verify that there was good ease in using the method.
Keywords: Trigonometry. GeoGebra. Teaching.
1 INTRODUÇÃO
Pesquisas relacionadas ao ensino-aprendizagem mostram que para muitos alunos, a matemática é considerada uma área de difícil compreensão, por esse motivo, esta, se torna uma disciplina chata, motivo de desmotivação, no qual “um dos obstáculos imediatos ao sucesso na aprendizagem da Matemática diz respeito ao desinteresse dos estudantes com relação ao modo como esta é apresentada em sala de aula” (Miguel, et al. 2009, p. 108).
Diante disso, cabe as instituições de ensino e aos professores de matemática, buscarem métodos que possam tornar o estudo desta disciplina mais significativo aos olhos dos alunos do ensino básico. Nessa percepção, uma alternativa que está cada vez mais presente é o uso das novas tecnologias em benefício de uma educação de mais qualidade. Assim,
as novas tecnologias podem reforçar a contribuição dos trabalhos pedagógicos e didáticos contemporâneos, pois permitem que sejam criadas situações de aprendizagem ricas, complexas, diversificadas, por meio de uma divisão de trabalho que não faz mais com que todo o investimento repouse sobre o professor (Perrenoud, 2000, p. 139).
Segundo Dantas (2015), a trigonometria é um dos conteúdos que muitos alunos demonstram dificuldades na sua compreensão, no qual destaca que entender as características das funções seno e cosseno ainda é um desafio muito grande para muitos discentes. Além de mostrar que é elevado a quantidade de estudantes que concluem o ensino médio sem ao menos estudarem trigonometria.
O presente trabalho tem a finalidade de apresentar os resultados obtidos no desenvolvimento do projeto, no qual, adotou o software GeoGebra como recurso pedagógico, objetivando tornar o ensino das funções seno e cosseno mais significativo, relatando os pontos positivos e negativos quanto a utilização do mesmo. O trabalho foi desenvolvido na turma do 2.º (segundo) ano do curso Técnico em Informática Integrado ao Ensino Médio do IFPI – Instituto Federal de Educação, Ciência e Tecnologia do Piauí, Campus São Raimundo Nonato Piauí.
Para tal, foi desenvolvido um curso de trigonometria com foco no ensino do seno e cosseno analisando o comportamento e suas características no ciclo trigonométrico, para a partir daí, realizar o estudo das funções seno e cosseno, tendo como recurso pedagógico principal a utilização do software GeoGebra. O objetivo geral, foi analisar quais as contribuições que o uso do programa traz para à aprendizagem do conteúdo citado acima.
Para alcançar tal meta, buscou-se atingir os seguintes objetivos específicos:
a) Identificar quais contribuições que o uso do software GeoGebra traz para aprendizagem das funções seno e cosseno aos alunos do 2.° ano do ensino médio.
b) Analisar se os alunos são capazes de resolverem determinados problemas envolvendo funções seno e cosseno através do uso do GeoGebra.
c) Verificar os pontos positivos e negativos na utilização do software para aprendizagem das referidas funções.
2 Novas tecnologias no ensino de matemática: uso do GeoGebra no ensino da trigonometria.
Com o surgimento da tecnologia da informática, abriu novos horizontes para o ensino da matemática, pois com a inserção dos computadores no processo de ensino, desenvolveram-se diversos softwares educacionais para auxiliar o professor na abordagem do conteúdo, e aos alunos na compreensão dos mesmos.
Um software pode ser considerado educacional quando adequadamente utilizado em uma relação de ensino-aprendizagem. As características principais que distinguem um software educativo é o seu desenvolvimento fundamentado em uma teoria de aprendizagem e a capacidade em que um aluno tem de construir, de forma autônoma, o conhecimento sobre um determinando assunto. (Jucá, 2006, p. 1).
Utilizar a tecnologia da informática no processo de ensino-aprendizagem é um método bem interessante, pois vivemos na era digital, onde as pessoas passam boa parte do tempo conectadas. O uso deste método poderá prender mais a atenção do aluno com relação ao assunto trabalhado, proporcionado melhores resultados. Na qual,
a escola não pode ignorar o que se passa no mundo. Ora, as novas tecnologias da informação e da comunicação (TIC ou NTIC) transformam espetacularmente não só nossas maneiras de comunicar, mas também de trabalhar, de decidir, de pensar (Perrenoud, 2000, p. 125).
Considerando que as escolas estejam equipadas com laboratórios de informática, o professor terá vários softwares para auxiliar no ensino. Praticamente todas ás áreas da matemática possui softwares que podem ser utilizados como ferramentas pedagógicas, buscando proporcionar um ensino diferenciado e de qualidade.
Dentre estes softwares, está o GeoGebra, uma ferramenta que pode ser utilizada em diversos ramos da matemática, inclusive no ensino das funções Seno e Cosseno, as quais serão o foco de estudo do presente trabalho. O mesmo, é uma ferramenta de licença gratuita, mas poderosa, utilizada nos vários ramos da matemática e estatística.
Criado por Markus Hohenwarter, o GeoGebra é um software livre de Matemática dinâmica desenvolvido para o ensino e aprendizagem da Matemática desde o ensino básico até o ensino universitário. Este software reúne recursos de geometria, álgebra, tabelas, gráficos, probabilidade, estatística e cálculos simbólicos em um único ambiente, com a vantagem didática de representar, ao mesmo tempo e em um único ambiente visual, as características geométricas e algébricas de um mesmo objeto. (DANTAS, 2015, p.145).
Uma das vantagens da utilização do GeoGebra é a possibilidade do aluno interagir com as construções no ambiente gráfico do software, permitindo que este, manipule figuras criadas sem muitas dificuldades, de modo a compreender melhor o conteúdo no qual está estudando.
Um dos conteúdos que o uso do GeoGebra pode contribuir na sua abordagem é o da trigonometria, que segundo Dante (2008, p. 269) “A trigonometria (trigono = triângulo; metria = medida) teve origem no estudo das relações entre as medidas dos lados e dos ângulos de um triângulo e em particular, do triângulo retângulo”. Sendo que “O uso do software pode auxiliar na resolução de problemas de trigonometria, especialmente em atividades investigativas, de forma que os estudantes possam interagir com as figuras construídas” (Lopes, 2011, p. 11).
A trigonometria continua sendo importante para o desenvolvimento do ser humano, na qual se desenvolveu em épocas e lugares distintos, se modificando ao longo dos anos para atender as necessidades em cada período.
A trigonometria, como a conhecemos hoje, na sua forma analítica, remonta ao século XVII. Seu florescimento depende de um simbolismo algébrico satisfatório, o que não existia antes dessa época. Mas, considerando o termo trigonometria no seu sentido literal (medida do triângulo), a origem do assunto pode ser situada já no segundo ou terceiro milênio antes de Cristo. (Iezzi, 2013, p. 36)
A trigonometria é um dos conteúdos matemáticos de ampla relevância devido ao grande número de aplicações, não somente em problemas restritos à matemática, mas também nas diversas disciplinas científicas como física, química etc. “Há inúmeras aplicações das relações trigonométricas entre triângulos quaisquer – na Física, por exemplo, para determinar a intensidade da força à qual fica sujeito a um fio que suspende um objeto em equilíbrio”. (Dante, 2010, p. 9).
As funções trigonométricas, são essenciais para o estudo de diversas áreas de natureza periódica.
Os fenômenos periódicos, aqueles que se repetem em intervalos regulares, são encontrados em várias áreas, como Música (a teoria da ressonância afirma a natureza matemática nas relações harmônicas), Acústica (no estudo dos meios de propagação do som), Eletricidade (no estudo do eletromagnetismo, equações matemáticas preveem ondas eletromagnéticas), Mecânica (no movimento circular uniforme), e nelas as funções trigonométricas são de grande aplicações. (Dante, 2010, p. 79).
Mesmo esse conteúdo sendo de fundamental importância para a sociedade, há grande rejeição por parte dos alunos devido à dificuldade de compreensão das propriedades trigonométricas. Essa rejeição em muitos casos é potencializada pelo despreparo de alguns professores ou pela falta de relevância dada por esses ao ensino da trigonometria, levando apenas os conceitos básicos ou até mesmo omitindo este conteúdo.
3 METODOLOGIA
Para o desenvolvimento do presente trabalho, foi realizado um levantamento de dados por meio de um questionário de sondagem aplicado na turma do 2.º ano de informática, objetivando colher informações a respeito do uso da tecnologia no ensino de matemática, identificando se estes já tiveram alguma experiência com softwares educacionais, inclusive o GeoGebra. Nessa etapa, 25 alunos responderam ao questionário, sendo esses estudantes o público na qual se direcionou a pesquisa.
Após a coleta e tabulação dos dados citados acima, foram ministradas 16 horas aulas referente ao estudo da trigonometria elementar, partindo da trigonometria no triângulo retângulo até a o conteúdo de transformações trigonométricas, para assim iniciar o estudos das funções seno e cosseno com auxílio do GeoGebra. Ressaltando que a abordagem desses conteúdos não era o foco principal do trabalho, porém, se fez necessária pelo fato de ser a base para o estudo do conteúdo programado.
Assim, ao concluir a etapa citada acima, foi dado início a um curso que teve duração de 10 horas aulas, no qual, adotou o Software GeoGebra como ferramenta pedagógica de apoio ao ensino das funções seno e cosseno, buscado tornar o estudo destas mais significativo aos olhos dos alunos. Na realização desse curso foram executadas as seguintes etapas:
1º etapa: o GeoGebra foi apresentado aos alunos, ensinando-os algumas funcionalidades básicas necessárias para a realização das atividades programadas.
2º etapa: foi ministrado um curso envolvendo o estudo do seno e cosseno no ciclo trigonométrico, de modo a analisar o comportamento destes em cada quadrante da circunferência trigonométrica, para a partir do ciclo criado gerar as funções seno e cosseno, analisando o comportamento gráfico das mesmas, de modo a identificar o domínio, imagem, período, crescimento e decrescimento com a determinação de cada quadrante do ciclo.
3º etapa: concluído a etapa 2º, foi introduzido o conteúdo das senoides do tipo y = a . sen(b . x + c ) + d e y = a . cos(b . x + c) + d, mostrando como estas se comportam com a variação dos parâmetros a, b, c e d. Sendo que nessa etapa foi realizado o estudo da influência dos parâmetros nas funções de forma separada, para posteriormente realizar o estudo envolvendo os quatro parâmetros de uma vez. O curso foi realizado em um laboratório de informática, no qual os alunos foram instigados a resolverem problemas específicos por meio do manuseio do software.
4º etapa: ao final das atividades propostas, foi aplicado dois questionários, o primeiro contendo 5 questões envolvendo o conteúdo trabalhado, onde os alunos foram provocados a resolverem sem o uso do GeoGebra, só com conhecimentos obtidos durante a execução do projeto. No segundo, o objetivo foi questioná-los sobre o uso do software nas atividades desenvolvidas, tendo as seguintes indagações: como avaliam o uso do GeoGebra no ensino das funções seno e cosseno? A sua aprendizagem tornou mais significativa por meio do uso desta ferramenta? Quais os pontos positivos e negativos na utilização do aplicativo? Houve dificuldade quanto a utilização do software?
Toda a discussão neste trabalho girará em torno das etapas citadas acima. Procurando analisar o desempenho dos alunos nas atividades desenvolvidas, e a opinião destes sobre o uso do software no ensino de trigonometria.
4 RESULTADOS E DISCUSSÕES
Inicialmente, foi aplicado um questionário diagnóstico para colher informações relevantes a respeito da formação básica dos alunos no ensino fundamental 1 e 2, e sobre possíveis uso de recursos tecnológicos no ensino de matemática como por exemplo o próprio GeoGebra durante essa formação inicial.
Por meio deste levantamento, identificou-se que dos alunos que se submeteram a pesquisa, 56% cursaram todo o ensino fundamental em escolas públicas, 32% em escolas particulares e 12% parte em escolas particulares parte em escolas públicas. Além disso, 56% do público pesquisado, disseram que seus professores já haviam utilizado métodos inovadores no ensino de matemática. As informações colhidas estão detalhadas na tabela 1.
Tabela 1: Informações relacionados a formação dos alunos.
Fonte: dados da pesquisa.
Ainda, no questionário citado acima os alunos foram questionados quanto ao uso da tecnologia em benefício do ensino de matemática, sendo que apenas 36% responderam que os professores em algum momento usaram recursos tecnológicos na explanação de determinados conteúdos, e destes, aproximadamente 56% expressaram já ter conhecido o GeoGebra. Isso evidência ainda mais que a tecnologia mesmo presente na contemporaneidade ainda não é aproveitada de modo a oportunizar uma educação de qualidade.
4.1 Atividades desenvolvidas utilizando o GeoGebra.
4.1.1 Estudo do ciclo trigonométrico com auxílio do GeoGebra.
Para os alunos se familiarizarem com o software GeoGebra foi trabalhado a construção da circunferência trigonométrica, para que assim pudessem realizar o estudo do comportamento do seno e cosseno em cada quadrante do ciclo. Sendo que uma circunferência trigonométrica é “a circunferência orientada cujo raio tem 1 unidade de comprimento e na qual o sentido positivo é o anti-horário”. (DANTE, 2010, p. 34).
Para facilitar o contato dos estudantes com o software na realização das atividades, foi disponibilizado uma apostilha tutorial contendo todo o conteúdo a ser trabalhado, detalhando o passo a passo das construções a serem realizadas. Nessa atividade foram dispostos elementos fundamentais para uma melhor compreensão no estudo, por meio da interação em ambiente gráfico.
Figura 1 – ciclo trigonométrico.
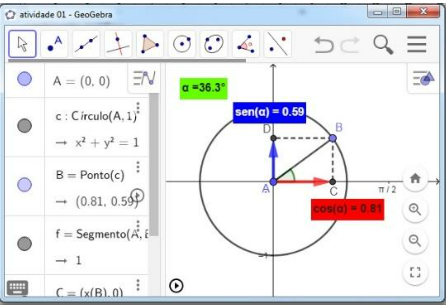
Fonte: dados da pesquisa.
Com a construção da circunferência concluída, representada pela imagem acima, foi proposto aos estudantes que realizassem o estudo do comportamento dos sinais do seno e cosseno em cada um dos quadrantes. Baseando-se na figura 1,

Posteriormente a realização da atividade acima, os alunos realizaram o estudo de simetrias em relação ao eixo vertical, eixo horizontal e em relação ao centro do ciclo trigonométrico por meio da construção, utilizando os seletores de ocultar/exibir objeto e animar, recursos presentes no GeoGebra. Dessa forma, foi possível mostrar que para se determinar o seno ou cosseno de um ângulo do 2º, 3º ou 4º quadrante, basta compará-los com seus correspondentes no 1º quadrante. Através do estudo, foi possível mostrar de forma clara que dado o ângulo x ∈ 2° quadrante temos que
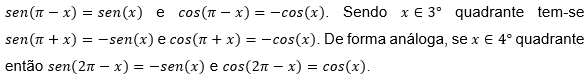
Nessa etapa, a utilização do software foi de fundamental importância visto que por meio deste, os alunos tiveram uma visão mais realística do conteúdo estudado, através da manipulação no ambiente gráfico do software.
4.1.2 Gerando as funções y = sen(x) e y = cos(x) por meio do ciclo trigonométrico.
Nessa etapa foi introduzido o estudo da função seno e função cosseno, utilizando a construção anterior para gerar os gráficos das funções a partir do movimento do vértice da hipotenusa não adjacente ao ângulo , do triângulo ABC inscrito na circunferência trigonométrica. Os gráficos gerados estão representados nas figuras abaixo.
Figura 2: gráfico da função y=sen x
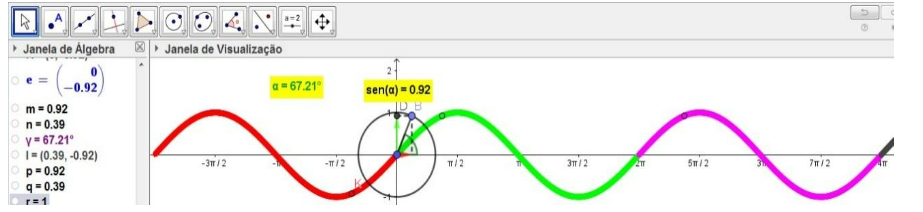
Fonte: dados da pesquisa
Figura 3: gráfico da função y= cos x
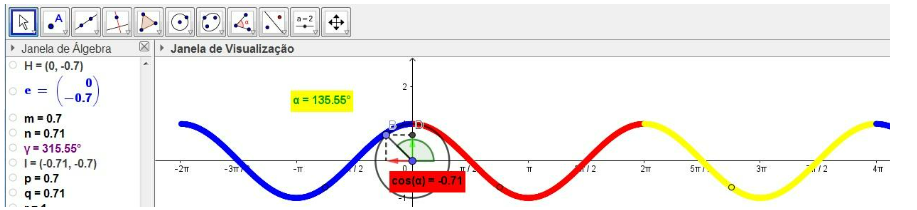
Fonte: dados da pesquisa.
Os alunos realizaram o estudo dos gráficos construídos, analisando como é o comportamento de cada um, identificando o domínio, imagem, analisando a paridade, periodicidade e realizando o estudo do crescimento e decrescimento de cada função.

4.1.3 Estudo das senoides: um olhar por meio do software GeoGebra.
Com o estudo acima concluído, foram apresentados as senoides do tipo
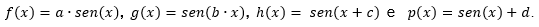
Nessa etapa, o objetivo foi analisar como se comportam os gráficos das referidas funções, por meio da variação dos parâmetros a, b, c e d. Analisando cada parâmetro separadamente.
Inicialmente, os alunos construíram alguns gráficos das funções no GeoGebra com variações no parâmetro a, posteriormente construíram outros gráficos com variações em b, c, e d respectivamente, analisando o comportamento de cada gráfico conforme a variação dos parâmetros.
Os gráficos construídos estão dispostos nas quatro figuras abaixo, cada um representa a variação dos parâmetros a, b, c e d nessa ordem.
Figura 4: gráficos da função fx=asen(x).
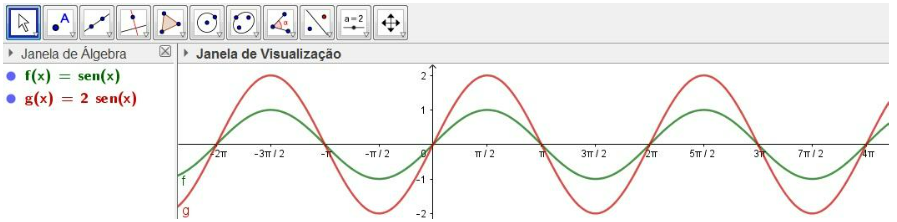
Fonte: dados da pesquisa.

Figura 5: gráfico da função gx=sen(bx).
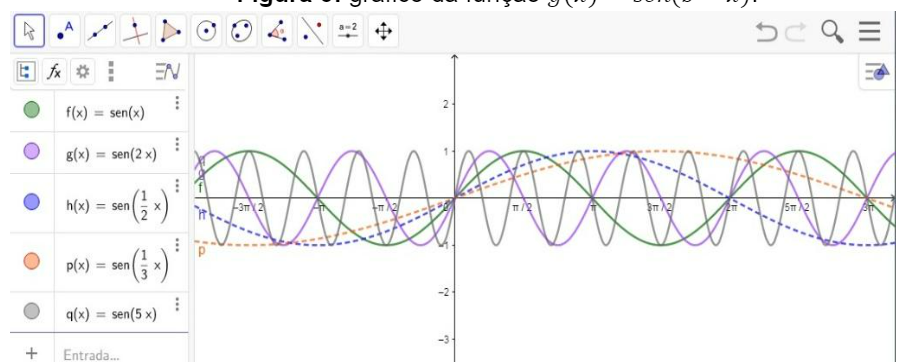
Fonte: dados da pesquisa.

Figura 6: gráfico da função hx=sen(x+c).

Fonte: dados da pesquisa.
Com características semelhantes ao comportamento de px=sen(x), a função px=senx+d com variações realizadas no parâmetro d, tem como única alteração sofrida no gráfico o deslocamento sobre o eixo y. Mostrou-se, que quando d se desloca no sentido positivo o gráfico da função tende a se deslocar no sentido positivo em relação ao eixo y, quando d se desloca no sentido negativo, o gráfico tende a se deslocar no sentido negativo sobre y, como exposto no seguinte gráfico.
Figura 7: gráfico da função px=senx+d.
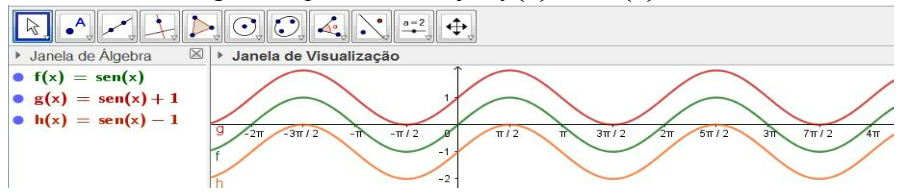
Fonte: dados da pesquisa.

Assim, concluiu-se a parte da aplicação na qual previa a utilização do GeoGebra como recurso pedagógico, na explanação do conteúdo programado.
4.2 Análise e discussões sobre a eficácia do uso do GeoGebra no ensino da trigonometria.
Este artigo não tem a finalidade de comparar resultados através da aplicação de pré-testes e pós-testes para verificar se a utilização do software GeoGebra é ou não eficaz por meio de análises quantitativas. A intenção principal foi identificar quais as contribuições que o uso do software oferece ao ensino da trigonometria, por meio do desempenho dos alunos durante a realização de cada atividade, observadas através de um olhar crítico, analisando o grau de facilidade ou dificuldade em concluir cada uma das etapas propostas, e questionando-os, como avaliam o uso do programa como ferramenta pedagógica no ensino de trigonometria.
4.2.1 Discussão sobre as atividades desenvolvidas.
No desenvolvimento das atividades propostas, alguns tiveram mais, outros menos dificuldades na realização de cada etapa, sendo que a maioria dos alunos conseguiram resolver mais de 80% dos 11 problemas presentes no tutorial. As atividades do tutorial foram divididas em quatro partes, que foram: estudo do seno e cosseno no ciclo trigonométrico, estudo da função seno, estudo da função cosseno e estudo das senoides.

“A função se desloca sobre o eixo y de acordo com o valor atribuído a d, e consequentemente a imagem vai alterar o intervalo dependendo da variação do d”. (ALUNO A)
“O comportamento vai mudar de acordo com o número somado ou subtraído, a imagem vai mudar dependendo do valor somado ou subtraído a função f(x) = sen (x) ”. (ALUNO B)
Um ponto positivo identificado na resolução dessa atividade é que, os alunos tiveram liberdade para responder de acordo com sua compreensão, visto por exemplo que os alunos A e B responderam o mesmo problema com argumentos expostos de formas diferentes, sem perder a qualidade da reposta. Evitando assim, apenas memorizar um padrão para solucionar determinados problemas.
Os discentes obtiveram bom desemprenho em um outro questionário contendo cinco problemas específicos, no qual, foram instigados a responderem sem o auxílio do software. Um dos problemas que teve 100% de acerto foi item 2, onde se pedia para determinar o período de cada uma das seguintes funções:
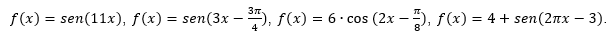
Nesse item foi possível perceber de forma mais concreta, que a maioria dos alunos compreenderam de fato o conteúdo trabalhado. No qual, todos identificaram que para determinar o período de uma senoide basta fazer 2πc, onde c é o valor que está sendo multiplicado por x.
No item 3 desse mesmo questionário houve 65% de acerto, sendo que, o problema sugeria aos alunos a identificarem os valores dos parâmetros a e b na função do tipo y = a + b * sen (x) representada pelo gráfico abaixo:

Nessa atividade os alunos perceberam que a variação do parâmetro a faz a função deslocar sobre o eixo y, e a variação do parâmetro b faz a função aumentar ou diminuir a imagem da função de acordo com o sentido da variação, assim, a maioria associou a alternativa correta, que era a = 1 e b = -2.
Observe que, alguns dos parâmetros foram mudados de ordem, aumentando ainda mais o grau de dificuldade, mas, mesmo assim a maioria dos alunos conseguiram associar a função de cada parâmetro, mostrando que de fato tiveram uma aprendizagem significativa, e não apenas decorativa.
4.2.2 Discussão através das percepções dos alunos.
Por meio da aplicação de um questionário final, os alunos foram indagados sobre como avaliam o uso do GeoGebra no ensino das funções seno e cosseno. Os dados colhidos estão apresentados na tabela 2.
Tabela 2: análise dos alunos em relação ao uso do GeoGebra no ensino das funções seno e cosseno.
Fonte: dados da pesquisa.
A análise positiva feita pela maioria dos alunos em relação a utilização do software, torna evidente que é de fundamental importância a adoção deste recurso como uma ferramenta pedagógica que venha contribuir no ensino. Além da aceitação de 92% dos estudantes, contando as indicações de bom, interessante e necessário, 76% justificaram a importância da utilização do mesmo. Para o aluno C “O geogebra é um software que ajuda a melhorar o estudo sobre trigonometria, e ajuda muito no entendimento e na hora de resolver questões que envolvam o estudo do seno e cosseno”. Para o aluno D a utilização do GeoGebra é interessante, pois segundo o mesmo este “é um jeito mais dinâmico de aprender trigonometria”.
Nestes dois comentários, os alunos “C” e “D” mostram a importância do uso do GeoGebra, onde o estudante C comenta a respeito da melhor compreensão do assunto estudado, principalmente no entendimento durante a resolução de problemas. O aluno D argumenta que por meio da utilização do programa as aulas ficam mais dinâmicas, e consequentemente facilita a aprendizagem.
Outro ponto a ser destacado é que 68% dos alunos argumentaram que o(a) professor(a) de matemática deve utilizar o GeoGebra com mais frequência, pois as aulas ficam mais dinâmicas, e produtivas, saindo da mesmice do cotidiano das aulas tradicionais.
A discussão acima enfatiza alguns pontos importantes quanto a utilização do GeoGebra, pode-se destacar entre estes que: aumenta a possibilidade da aprendizagem dos alunos por meio de atividades práticas, além de ser uma metodologia que possibilita sair dos moldes tradicionais de educação, visto que a inovação nos métodos de ensino é uma tendência a se seguir nos padrões e exigências da sociedade atual.
4.2.3 pontos positivos e negativos observados no uso do GeoGebra.
Ainda sobre o questionário citado no tópico 4.2.2 deste trabalho, os estudantes foram questionados a respeito dos pontos positivos e negativos quanto a utilização do software. Em relação aos pontos positivos os alunos destacam a facilidade de se realizar a interpretação gráfica das funções trabalhadas, e a possibilidade de ver na prática o comportamento dos gráficos de várias funções ao mesmo tempo, além de poder utilizar recursos tecnológicos em benéfico da aprendizagem. “Com o uso do GeoGebra as aulas são mais divertidas, facilita a aprendizagem, e tem tudo a ver com o curso”. (Aluno E)
Quanto aos pontos negativos, o principal argumento foi de ser uma ferramenta complexa, sendo que 48% disseram ter tido dificuldade no manuseio do programa, relatando que faltou um minicurso de como utilizar o GeoGebra, com todas as instruções mais básicas necessárias para realização das atividades.
5 CONSIDERAÇÕES FINAIS
No decorrer das atividades, procurou-se identificar se o GeoGebra facilita a aprendizagem dos alunos no estudo da trigonometria, com foco no estudo das funções seno e cosseno. Também objetivou analisar através da percepção dos estudantes a importância da utilização do programa no ensino de matemática.
Com as atividades desenvolvidas no 2º ano do ensino médio do IFPI campus São Raimundo Nonato Piauí, percebeu-se que a maioria dos alunos se mostraram bem participativos, de fato, envolvidos nas atividades propostas. Isso evidenciou que o uso do GeoGebra em muitos casos se faz necessário, pois os alunos vivenciam na prática o estudo gráfico das funções por meio da interação em ambiente gráfico, uma abordagem rica, proporcionando aos mesmos uma aprendizagem significativa, o que não seria tão viável sem o uso do método.
Através da análise no decorrer de cada etapa do projeto, e por meio dos dados obtidos com a aplicação de questionários, foi possível identificar que os alunos tiveram uma boa aceitação quanto a utilização do recurso no estudo da trigonometria, no qual a maioria dos alunos conseguiram concluir as atividades propostas, mostrando bom desempenho no entendimento das propriedades no estudo das funções seno e cosseno. Na percepção dos alunos, o uso do GeoGebra é de grande importância, visto que este possibilita a vivência na prática, melhorando a possibilidade do estudo gráfico, além de tornar as aulas mais dinâmicas e divertidas, saindo dos moldes tradicionais.
O desempenho dos alunos foi considerado notável, visto que este foi o primeiro contato dos estudantes com o conteúdo, e mesmo sendo um assunto de difícil compreensão a maioria obtiveram bons resultados na aprendizagem. Isso foi possível perceber por meio das atividades trabalhadas presentes no tutorial, e através do teste contendo cinco problemas relacionados ao conteúdo estudado, além das percepções dos estudantes obtidos por meio de relatos escritos.
De fato, o uso do GeoGebra facilita a aprendizagem dos alunos no estudo da trigonometria, no qual se abre um leque de possibilidades no estudo e compreessão do conteúdo. Mas, vale ressaltar que a utilização de recursos tecnológicos como este nem sempre será viável, às vezes será muito mais interessante utilizar materiais concretos, por exemplo. Isso vai depender de turma para turma, observando que no desenvolvimento do presente trabalho, mesmo sendo em uma turma de informática, nem todos os alunos conseguiram se adaptar ao recurso utilizado.
É fundamental que os professores estejam qualificados adequadamente para se utilizar recursos tecnológicos na abordagem de determinados conteúdos, não basta apenas ter intenção, tem que preparar as atividades coerentemente, e o mais importante, identificar se a turma na qual será desenvolvido o trabalho está apta a aceitação daquele recurso. Pois de nada adiantará planejar uma atividade na qual o perfil dos alunos não se encaixam.
Desse modo, concluímos que os objetivos do projeto foram alcançados, onde foi constatado que realmente o GeoGebra contribui significativamente com a aprendizagem dos aluno, desde que estes estejam aptos a utilização do recurso. Assim, espera-se que o presente artigo sirva de base para o desenvolvimento de outros trabalhos, no qual objetive abordagens mais significativas de conteúdos relacionados ao ensino da matemática, por meio do uso do GeoGebra, fazendo as modificações necessárias de acordo com os fins almejados.
REFERÊNCIAS
BARBOSA, J. L. M. Geometria Euclidiana Plana. 11. ed. Rio de Janeiro: SBM, 2012.
DANTAS, A. S. O uso do GeoGebra no ensino de trigonometria: uma experiência com alunos do ensino médio. Ciência e Natura, Santa Maria, v. 37. ed. P. 144 – 155, 2015. Disponível em: <https://periodicos.ufsm.br/cienciaenatura/article/viewFile/14503/pdf >. Acesso em: 01 de março. 2017.
DANTE, L. R. Matemática: contextos e aplicações. 1. ed. São Paulo: Ática, 2010.
DANTE, L. R. Matemática: livro do aluno (Ensino médio) I. Titulo. 1. ed. São Paulo: Ática, 2004.
IEZZI, G. Fundamentos da Matemática Elementar, 3: Trigonometria. 9. ed. São Paulo: Editora Saraiva, 2013.
JUCÁ, S. C. S. A relevância dos softwares educativos na educação profissional. Ciências e Cognição, Ceará, v. 8, agosto. 2006. Disponível em: < http://cienciasecognicao.org/pdf/v08/cec_vol_8_m32689.pdf>. Acesso em: 16 de fevereiro. 2017.
LOPES, M. M. Contribuições do software geogebra no ensino e aprendizagem de trigonometria. XIII CIAEM-IACME, Recife, Brasil, 2011. Disponível em: <https://ciaem-redumate.org/ocs/index.php/xiii_ciaem/xiii_ciaem/paper/view/2577> Acesso em: 02 de abril. 2018
MIGUEL, A. et al. História da Matemática em Atividade Didáticas. 2.ed. rev. São Paulo: Editora Livraria da Física, 2009.
PERRENOUD, P. Dez novas competências para estudar / Philippe Perrenoud; trad. Patrícia Chittoni Ramos. Porto Alegre: Artmed, 2000.
Questionários
ALUNO C, Estudante do 2º ano de informática do IFPI campus São Raimundo Nonato: [Relato escrito realizado em 27 de novembro de 2018]. Questionário. São Raimundo Nonato PI, 2018. Relato Escrito concedido ao artigo “USO DO GEOGEBRA NA APRENDIZAGEM DAS FUNÇÕES SENO E COSSENO: UMA EXPERIÊNCIA COM ALUNOS DO 2º ANO DO ENSINO MÉDIO” do IFPI – Instituto Federal de Educação, Ciência e Tecnologia do Piauí, Campus São Raimundo Nonato Piauí.
ALUNO D, Estudante do 2º ano de informática do IFPI campus São Raimundo Nonato: [Relato escrito realizado em 27 de novembro de 2018]. Questionário. São Raimundo Nonato PI, 2018. Relato Escrito concedido ao artigo “USO DO GEOGEBRA NA APRENDIZAGEM DAS FUNÇÕES SENO E COSSENO: UMA EXPERIÊNCIA COM ALUNOS DO 2º ANO DO ENSINO MÉDIO” do IFPI – Instituto Federal de Educação, Ciência e Tecnologia do Piauí, Campus São Raimundo Nonato Piauí.
ALUNO E, Estudante do 2º ano de informática do IFPI campus São Raimundo Nonato: [Relato escrito realizado em 27 de novembro de 2018]. Questionário. São Raimundo Nonato PI, 2018. Relato Escrito concedido ao artigo “USO DO GEOGEBRA NA APRENDIZAGEM DAS FUNÇÕES SENO E COSSENO: UMA EXPERIÊNCIA COM ALUNOS DO 2º ANO DO ENSINO MÉDIO” do IFPI – Instituto Federal de Educação, Ciência e Tecnologia do Piauí, Campus São Raimundo Nonato Piauí.
