THEORETICAL AND EXPERIMENTAL EVALUATION OF PHOTOVOLTAIC PUMPING SYSTEMS
REGISTRO DOI: 10.5281/zenodo.10393597
Gabriel Bastos de Souza Silva1
Wanderley Sena dos Santos2
Wilson Negrão Macêdo3
Resumo
O sistema fotovoltaico de bombeamento representa uma solução sustentável para proporcionar acesso à água potável em comunidades remotas da região amazônica, seja para consumo humano ou para a irrigação agrícola, em áreas com limitações de fornecimento elétrico pela concessionária local. Um componente central desse sistema é a motobomba, encarregada de fazer a sucção do fluido e conduzi-lo por meio de um sistema de tubulação até o destino desejado, e está frequentemente associada a um dispositivo de condicionamento de potência. No entanto, devido à utilização de sistemas fotovoltaicos, é comum que a motobomba opere em faixas de frequência abaixo do nominal, o que resulta em um rendimento inferior, em comparação com situações cujo fornecimento de energia é constante pela rede elétrica local. Diante disso, o presente estudo propõe uma abordagem baseada em equações teóricas dos componentes do sistema, com o objetivo de prever um ponto de operação otimizado da bomba, por meio dos fatores que afetam o desempenho do gerador fotovoltaico, como a irradiância solar e a sua temperatura. Para isso, o laboratório do Grupo de Estudos e Desenvolvimento de Alternativas Energéticas dispõe de uma bancada de simulação de alturas manométricas, empregada para comparar o desempenho de um sistema fotovoltaico de bombeamento com as simulações realizadas em Matlab desenvolvido em uma tese de doutorado defendida no Programa de Pós-Graduação em Engenharia Elétrica da Universidade Federal do Pará. Os resultados evidenciaram a eficácia da metodologia em indicar um ponto de melhor eficiência desses sistemas. Embora em algumas situações a operação real tenha apresentado discrepâncias em relação ao previsto, de modo geral, esse modelo se revelou valioso para orientar a implementação de sistemas fotovoltaicos de bombeamento com eficiência energética aprimorada, resultando em um incremento na produção de água e em menores perdas de energia.
Palavras-chave: Sistemas fotovoltaicos de bombeamento. Pontos de operação. Simulação. Curvas de performance.
INTRODUÇÃO
O acesso à água potável é um direito universalmente reconhecido e vital para a humanidade, conforme estabelecido pela Resolução 64/292/2010 da ONU. No Brasil há a Lei No 11.445 que estabelece a universalização no acesso ao saneamento básico, que inclui o abastecimento de água (Brasil, 2007). No entanto, essa premissa é frequentemente questionada diante da realidade global, onde a escassez da disponibilidade desse recurso essencial é uma triste realidade (Bordalo, 2022; Souza et al., 2012).
É crucial entender não apenas a disponibilidade da água, mas também da sua essencialidade tanto para a saúde, como para a agricultura e o desenvolvimento sustentável, principalmente em comunidades remotas e isoladas, regiões onde há menor desenvolvimento e acesso à energia elétrica (Bordalo, 2022; Souza et al., 2012). Em vista disso, algumas ideias são apresentadas com o objetivo de melhorar a situação dessas populações.
Este estudo aborda os sistemas fotovoltaicos de bombeamento (SFB) como uma alternativa viável para essas comunidades com restrições de acesso à energia elétrica da rede local, e garantir um mecanismo adequado à água potável de poços. Esses sistemas são, em geral, compostos por: geradores fotovoltaicos (GFV), dispositivos de condicionamento de potência (DCP) e motobombas. Essas últimas são disponibilizadas em uma ampla variedade de modelos, adequados para diferentes propósitos e níveis de vazão. Muitas delas apresentam curvas de desempenho confiáveis que orientam sobre as faixas ideais de altura manométrica (H) para otimizar o rendimento (Karassik et al., 2001; Santos, 2022).
Entretanto, essas curvas são elaboradas considerando o uso com um sistema de energia convencional, cuja frequência de operação é mantida no seu valor nominal constantemente. Para geradores FV, há o impactado pela variação intermitente da incidência de luz nos módulos FV, afetando a potência disponível para a bomba. Essa variação resulta em uma operação em frequências de rotação diferentes da nominal, o que pode acarretar um desempenho inferior do SFB caso utilize o ponto máximo de eficiência nominal (PME).
Para contornar esse desafio, foi proposto a aplicação de uma metodologia, a qual foi introduzida por Santos (2022) e Muñoz et al. (2015), para obter um novo ponto de operação da motobomba. Essa abordagem se baseia em cálculos matemáticos usando o perfil de irradiância e temperatura de operação da célula para determinar um ponto de operação ideal para a motobomba, considerando as condições climáticas da região. O objetivo é compreender como o clima de uma região influencia o desempenho de um SFB e, a partir disso, indicar a melhor configuração de instalação para obter a maior eficiência na captação de água.
Nesse estudo, aplicou-se essa metodologia no programa de cálculo computacional em Matlab, a fim de realizar diferentes simulações para obter o ponto de máxima eficiência solar (PMES) de um determinado SFB. Realizaram-se testes operacionais em uma bancada simuladora de pressão, abrangendo diversos cenários com alturas manométricas variadas, para analisar o seu desempenho.
1. FUNDAMENTAÇÃO TEÓRICA OU REVISÃO DA LITERATURA
1.1 Conceitos gerais de sistemas fotovoltaicos de bombeamento
Um SFB típico é uma alternativa aos sistemas convencionais de bombeamento. Ele é composto basicamente por um gerador fotovoltaico, um dispositivo de condicionamento de potência e uma motobomba, com a possibilidade de adicionar um sistema de armazenamento e uma rede de distribuição, por meio das tubulações (Figura 1.1). A água adquirida pode ser usada para irrigação, consumo animal, humano, sendo o último de uso coletivo ou individual (Silva, 2019).
Figura 1.1 – Ilustração de um sistema fotovoltaico de bombeamento.

Fonte: Adaptado de World Bank (2018).
O GFV capita a energia solar e converte em energia elétrica, podendo ser utilizado em locais remotos, porém, como a irradiância solar tem característica intermitente, a potência do GFV é influenciada conforme o clima e a posição do sol. Dessa forma, há momentos do dia em que haverá pouca ou nenhuma produção de água e para contornar isso, instalam-se sistemas de armazenamento para atender a população durante a baixa capacidade do GFV, com opções como: baterias e reservatórios de água (World Bank, 2018). O SFB dispõe de diferentes configurações, cuja escolha depende do objetivo do sistema, da disponibilidade financeira, de como será feita a sucção da água e entre outros, as quais são analisadas pelo projetista. A Figura 1.2 exibe alguns diferentes exemplos de arranjos que podem ser utilizados para compor um sistema fotovoltaico de bombeamento, como a inclusão ou não de um rastreador da posição solar, além das diversas opções de uso DCP e motobombas (Morales, 2016), a fim de melhor se adequar a situação imposta.
Figura 1.2 – Diagrama de diferentes tipos de configurações de SFB.

Fonte: Adaptado de Morales (2016).
Macintyre (1997) define bombas como geratrizes, pois realizam o deslocamento de um fluido por escoamento, a partir da transformação do trabalho mecânico em energia hidráulica, por uma tubulação. As bombas são classificadas em dois grandes grupos: as de deslocamento positivo e as centrífugas.
O DCP, por sua vez, converte a tensão de corrente contínua (c.c.) do barramento do GFV em corrente alternada (c.a.) para a motobomba c.a. – geralmente em frequência variável – ou apenas ajusta a tensão para uma motobomba c.c. Ele possui um conjunto de circuitos eletrônicos de potência para otimizar o controle da energia do GFV e seu aproveitamento para determinada aplicação. Ele pode estar integrado à carcaça da motobomba ou separado em um compartimento externo (Brito, 2006; Pinho et al., 2008). Existem vários modelos no mercado, muitos deles próprios para SFB, que incluem algumas medidas de segurança e um circuito eletrônico para o seguimento do ponto máximo de potência (SPMP) do GFV, conforme as mudanças do clima.
1.2 Curvas de sistemas de bombeamento
A Figura 1.3 ilustra uma típica instalação de um sistema de bombeamento. A definição de altura manométrica (H) é o desnível entre um ponto de captação até a descarga para o reservatório e sua unidade é dada em metros de coluna d’água (mca). A altura estática (HE) é o desnível no ponto da superfície líquida e, conforme a bomba realiza a sucção do fluido no poço, ocorre um rebaixamento (HR), onde o nível da superfície do líquido é reduzido ao redor da tubulação, do estático para o dinâmico. A soma das duas alturas é representada por HD, denominada de altura dinâmica (Santos, 2022; Macintyre, 1997). As perdas são identificadas por J, resultadas do atrito do fluido em contato com as paredes da tubulação, e são diretamente proporcionais ao quadrado da vazão aplicada pela bomba (Karassik et al., 2001).
Figura 1.3 – Instalação hidráulica típica.
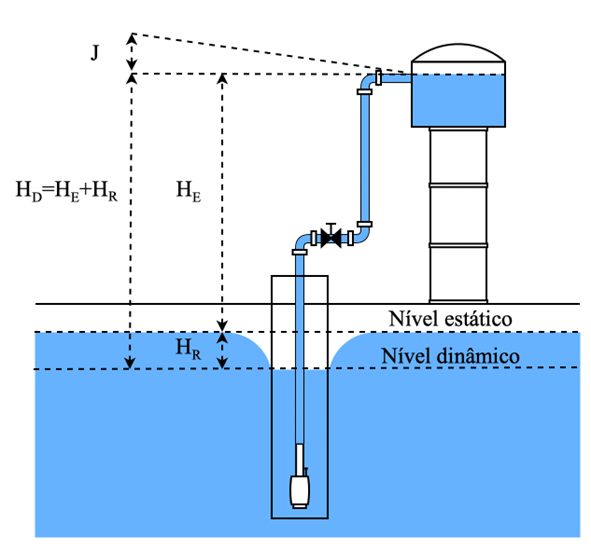
Fonte: Elaborado pelo autor, baseado em Santos (2022) e Macintyre (1997).
A depender da vazão e do sistema de tubulação, as perdas podem ser desprezíveis, resultando em uma altura manométrica constante. A Figura 1.4 apresenta as curvas reais e aproximadas do sistema e as curvas características da bomba, estas que relacionam a vazão com a altura manométrica (curva H-Q) e com o rendimento (curva h-Q). O ponto comum da interseção da curva H-Q com a do sistema é o ponto de trabalho da bomba na instalação hidráulica, e ela deve estar, na medida do possível, próximo ao maior rendimento do sistema, denominado neste trabalho de ponto máximo de eficiência (PME), baseado em Karassik et al. (2001) e Santos (2022). As fabricantes podem fornecer tabelas e gráficos com as relações de H-Q e h-Q para demonstrar a performance e a eficiência da motobomba. Por intermédio dessas, extraem-se as funções H(Q) e h(Q), importantes para realizar os cálculos de otimização do funcionamento das bombas nesse estudo.
Figura 1.4 – Curvas características da bomba.
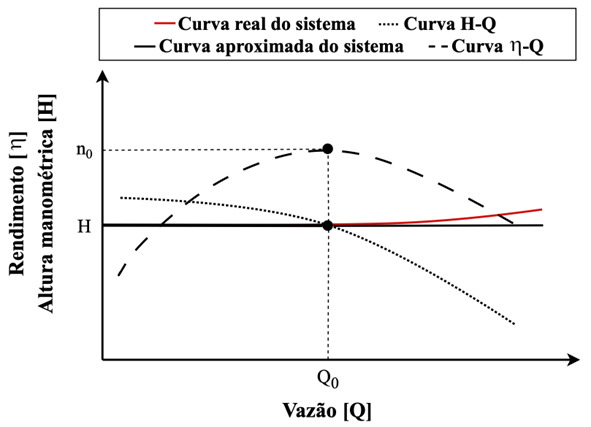
Fonte: Elaborado pelo autor do trabalho.
Em um sistema convencional, a bomba centrífuga é suprida por uma potência constante, que garante a operação na frequência de rotação nominal da bomba em 60 Hertz (Hz), valor adotado no Brasil. No entanto, em sistemas de bombeamento supridos por GFV a situação é diferente, pois a velocidade de rotação varia a medida da disponibilidade da irradiância solar incidente e, constantemente, opera em distintas faixas de frequência de rotação abaixo do nominal (Figura 1.5).
Figura 1.5 – Modificação das curvas H-Q e h-Q e PME com a velocidade de rotação.
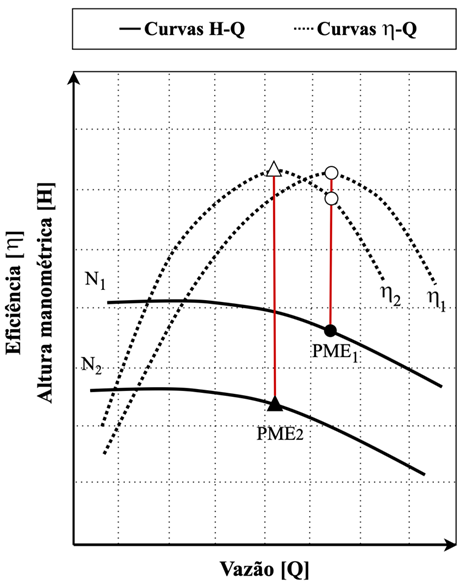
Fonte: Elaborado pelo autor, baseado em Macintyre (1997).
Como mostra o gráfico, outra velocidade de rotação da bomba gera outro ponto otimizado de eficiência. Assim, ao obter diferentes pontos máximo de eficiência durante o dia, a média será inferior ao PME apontado pela fabricante, e isso afeta diretamente na eficiência final do sistema (Santos, 2022). Com o tempo de uso da motobomba, é esperado a redução do seu rendimento com o tempo. Assim, aos poucos o PME é modificado para um ponto de operação diferente do nominal, até chegar em casos a qual a bomba não supre mais as necessidades do sistema, levando a sua substituição.
2. METODOLOGIA
Esse estudo propôs utilizar o método utilizado em Santos (2022) e Muñoz et al. (2015) para encontrar o ponto máximo de eficiência solar, o PMES, a partir do perfil de irradiância e da temperatura de operação da célula fotovoltaica, para obter equações analíticas que visam prever a faixa operacional da bomba centrífuga e determinar o ponto de operação otimizado médio, assim como a eficiência e o provável acúmulo de água ao final do dia. Para este artigo, aplicou-se para comparar o uso do PME e do PMES em um determinado sistema fotovoltaico de bombeamento.
Essa estratégia depende das características de cada componente do SFB: as potências do GFV e da motobomba, suas curvas de desempenho, mas, principalmente, do conhecimento da eficiência e conversão de energia de cada parte que constitui o sistema. A Figura 2.1 retrata uma configuração típica de um SFB.
Figura 2.1 – Configuração típica de um SFB.

Fonte: Elaborado pelo autor, adaptado de Santos (2022).
A ilustração mostra que a cada etapa de conversão de energia dos dispositivos do SFB, são geradas perdas, e isso afeta nas curvas de eficiência do sistema fotovoltaico de bombeamento, e determiná-las não é um processo simples. Cada equipamento gera perdas específicas, intrínsecas às suas características, as quais afetam a eficiência (Equação 2.1).

onde h é a representação da eficiência; PSAÍDA e PENTRADA são, respectivamente, a potência de saída e entrada de qualquer sistema.
2.1. Estimação das curvas de performance e de eficiência dos componentes
• Gerador fotovoltaico
O desempenho do SFB está diretamente proporcional a quantidade de energia recebida pelo GFV, logo, as informações relacionadas a sua potência nominal de referência (PMP, REF), e perdas por temperatura (gMP) devem ser apresentadas no programa para obter uma simulação mais equivalente à realidade. Elas são obtidas nas condições padrão de teste (STC), com valores definidos para uma irradiância de 1000 Watt por metro quadrado (W/m2), 25 graus Celsius (ºC) e massa de ar (AM) de 1,5. Com os dados de características da região, a irradiância (G) e a temperatura de operação da célula (TC), e do coeficiente gMP, é possível calcular a máxima potência teórica do GFV, PMP, mostrada na Equação 2.2.
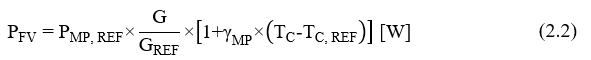
onde GREF e TC, REF são os valores de referência da irradiância e da temperatura do GFV, respectivamente, associados às condições de STC.
• Dispositivo de condicionamento de potência
A eficiência do DCP (hDCP) é a relação entre a energia (ou potência) de entrada do gerador fotovoltaico (PFV) e sua saída para o motor (PM). O seu valor depende da porcentagem de carregamento do inversor. Ela possui uma curva acentuada na faixa de 0 a 20 % de carga carregada no DCP, porém, após isso, ela é mantida relativamente estável. Baseado em valores teóricos da literatura, na carga nominal, hDCP fica próxima a uma faixa de 95-97 % (Santos, 2022). Como, em geral, os sistemas de bombeamento necessitam de uma potência mínima para iniciar a descarga de água, como foi apontado por Santos (2022), é improvável a atuação do bombeamento para até 20 % de carregamento do inversor. Assim, é possível considerar hDCP como uma constante para esse estudo.
• Motor
A eficiência do motor (hM) é dada pelo quociente da potência que supre a bomba (PB) e PM. Não são todas as fabricantes que fornecem o valor da eficiência máxima de um motor, muito menos a sua curva, e esta depende das características da sua carcaça, potência e torque. Não é indicado o uso do valor nominal de hM, pois assume que a máquina possuirá essa eficiência para todo nível de carga (Hsu et al., 1996). Para o DCP, considerar apenas o valor nominal é mais viável devido a curvatura da eficiência do DCP ser menos arqueada que a do motor, esta última que só possui maior estabilidade a partir de valores próximos 50 % do funcionamento da carga nominal (Figura 2.2).
Figura 2.2 – Curvas típicas da eficiência de motores.

Fonte: Adaptado de McCoy e Douglass(2014).
Necessitou-se o uso de uma função da curva de hM para a metodologia. Sem a disponibilidade dessa informação, Santos (2022) e Muñoz et al. (2015) interpolaram as típicas curvas de hM, fornecidas na literatura (NCR, 2004; Burt et al., 2008; McCoy e Douglass, 2014; Rivalin et al., 2018), e basearam na equação de estimação da curva de eficiência de inversores usados em sistemas fotovoltaicos conectados à rede (Schimdt, Jantsch e Schimd (1992) apud Zilles et al. (2012)) para realizar a interpolação da curva da eficiência do motor. Mediante as curvaturas típicas da Figura 2.2 o método foi aplicado, resultando a Equação 2.3.
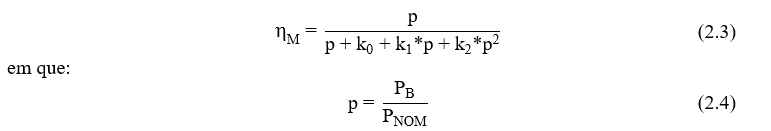
onde p é a potência de saída normalizada do motor, PB, em direção a bomba com relação à potência nominal (PNOM); os coeficientes k0, k1 e k2 são fatores relacionados às perdas do motor.
Entretanto, ressalta-se que a curva de 1 HP (@ 1,014 cv) da Figura 2.2 possui uma eficiência de motor, em 100 % da carga, próximo a 97 %. Assim, para hM nominal diferente, realiza-se uma calibração na curva, uma relação entre hM e o valor de 97 %, para adquirir os novos coeficientes.
• Bomba
Para as curvas H-Q e h-Q da bomba, extraem-se as funções de H(Q) e h(Q), mediante interpolação. Ulanicki, Kahler e Coulbeck (2008) e Santos (2022), aproximaram as curvas H-Q e h-Q a funções de segundo e terceiro grau, respectivamente (Equação 2.4 e 2.5).

No conceito da lei de similaridades, é descrito matematicamente uma relação direta entre as grandezas características de uma bomba centrífuga (potência de entrada da bomba, vazão, e a altura manométrica) em função da velocidade de rotação da bomba N (Karassik et al., 2001). Considerando as duas velocidades de rotação N1 e N2 da Figura 1.5 como, respectivamente, a frequência de rotação nominal (fN) e a frequência de operação atual da bomba (f), a equação da lei das similaridades pode ser escrita como:

onde Qf e Hf são os valores padrão para a frequência nominal de 60 Hz.
Por meio disso, ao usar as Equações 2.7 e 2.8 nas funções H(Q) e h(Q), criam-se funções de duas variáveis: Q e f, ambas inconstantes e dependentes uma da outra, resultando nas funções H(Q, f) e h(Q, f). Ao saber que h(Q,f) é relacionada a eficiência da bomba (hB), obtida na relação entre a potência hidráulica com a PB, forma-se o sistema não-linear composto pelas Equações 2.9 e 2.10.
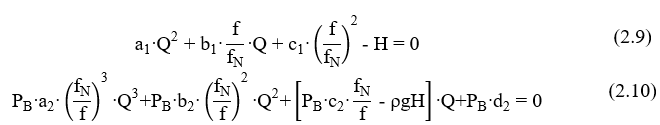
onde fN para as normas nacionais é 60 Hz; a densidade do fluido ρ para água aproxima-se a 997 kg/m3; a aceleração da gravidade g é de 9,8 m/s2 e são usadas para determinar a potência hidráulica (PH = ρ.g.H.Q).
2.2 Aquisição do PMES
O programa é iniciado com a inserção dos dados relacionados a motobomba, como a potência nominal da bomba e as alturas manométricas a serem simuladas no código, gerando o conjunto H = {H1, …, Hj, …, Hm} com m elementos. Para este trabalho, quaisquer conjuntos são representados por símbolos em negrito.
A irradiância e a temperatura de operação da célula são fornecidas respectivamente por células fotovoltaicas de referência e sensores de temperatura. Os seus valores são coletados a um certo intervalo de tempo, gerando dois conjuntos de variáveis com n elementos: G = {G1, …, Gi, …, Gn} e TC = {TC1, …, TCi, …, TCn}. Da posse desses dados, utilizou-se a Equação 2.2 para adquirir o conjunto da potência elétrica do GFV, PFV = {PFV1, …, PFVi, …, PFVn}. A partir do sistema linear compostas pelas Equações 2.10 e 2.11 a simulação gera os conjuntos vazão Q = {Q1, …, Qi, …, Qn} e frequência de operação f = {f1, …, fi, …, fn}.
No final, cada elemento de H gera um conjunto de Q e f, em que é possível calcular a eficiência do sistema para cada simulação da altura manométrica, que totaliza o conjunto hS = {hS1, …, hSj, …, hSm}, da mesma quantidade de elementos de H. O cálculo para obter cada elemento de hS é feito pela Equação 2.12, resultado da relação entre a energia total da bomba com a energia gerada pelo GFV para o sistema durante o dia.

Após isso, realiza-se uma comparação entre os elementos de hS para determinar qual elemento de H culminou na maior eficiência do sistema, o HPMES. Essa altura manométrica é o novo ponto de operação que a motobomba deve ser instalada para maior efetividade no fornecimento de água.
As curvas de isoeficiência (ou isorrendimento) são um conjunto de pontos da curva de performance da bomba em diferentes velocidades de rotação, cuja utilização da Lei das Similaridades, resultam em valores iguais de eficiência. A sua determinação é dada pela junção das Equações 2.7 e 2.8, que gera:

Se adicionar os limites de vazão nominal da bomba e suas respectivas alturas manométricas, criam-se duas curvas que delimitam os valores de Q que podem ser obtidos na simulação. A Figura 2.3 representa um fluxograma que resumo os passos do programa e as inserções dos dados que foram providas para a realização desta pesquisa.
Figura 2.3 – Fluxograma.
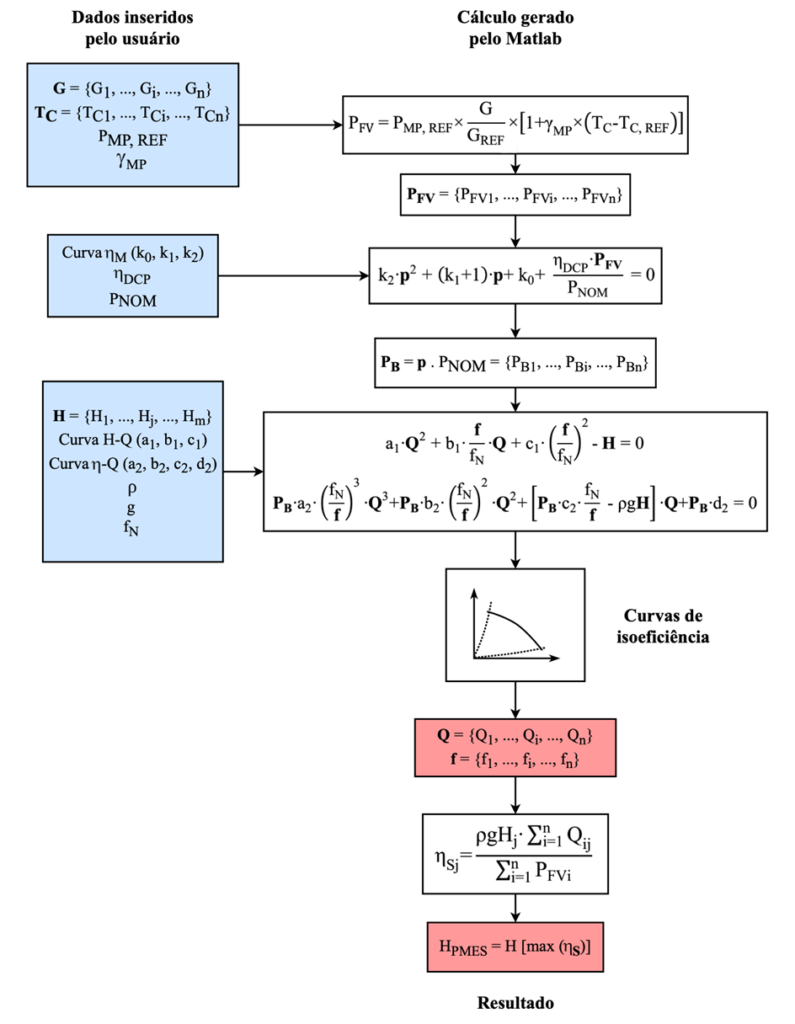
Fonte: Elaborado pelo autor do trabalho.
3. MATERIAIS UTILIZADOS
Os sistemas fotovoltaicos de bombeamento foram compostos por uma motobomba, dois controladores de bombeamento e dois geradores fotovoltaicos.
3.1 Motobomba
No catálogo da fabricante Leão S.A. (2023), é disposto alguns pontos de trabalho da motobomba para demonstrar a performance da 4R5-PA (Tabela 3.1).
Tabela 3.1 – Pontos de operação nominais da Leão 4R5-PA

Fonte: Elaborado pelo autor, adaptado de Leão S.A. (2023).
A motobomba apresenta uma potência nominal (PNOM) de 1 cv (735,5 W), porém não foram fornecidas informações sobre as curvas ou valores nominais da eficiência do motor e da bomba. Dessa forma, para hM, interpolou-se a curva típica ilustrada na Figura 2.2 para motobombas de 1 HP (aproximadamente 1 cv). Posteriormente, realizou-se uma calibração com o uso do seu valor nominal estipulado, para 100 % de seu carregamento. Recorreu-se a informações de outros modelos da mesma fabricante, Franklin Electric S.A. (2015), para obter um valor aproximado. Após análise de produtos similares, observou-se uma eficiência típica para o motor de 70 %. Com base nisso, foram determinados os coeficientes k0, k1 e k2, conforme apresentado na Tabela 3.2.
Tabela 3.2 – Valores dos coeficientes relacionados às perdas do motor para a curva de 1 HP.

Fonte: Elaborado pelo Autor.
As curvas H-Q e h-Q (Figura 3.1), foram obtidas mediante valores apresentados no catálogo e medições em laboratório para o cálculo da eficiência da bomba em diferentes pontos de operação. Nota-se que o ponto de máxima eficiência (PME) está próxima a 59,42%, a uma altura manométrica de 41,9 mca (HPME). Através de H(Q) e h(Q), retiraram-se as constantes derivadas a1, b1, c1, a2, b2, c2 e d2, expressas na Tabela 3.3.
Tabela 3.3 – Valores das constantes para a motobomba de referência.

Fonte: Elaborado pelo autor.
Figura 3.1 – Curvas H-Q e h-Q.
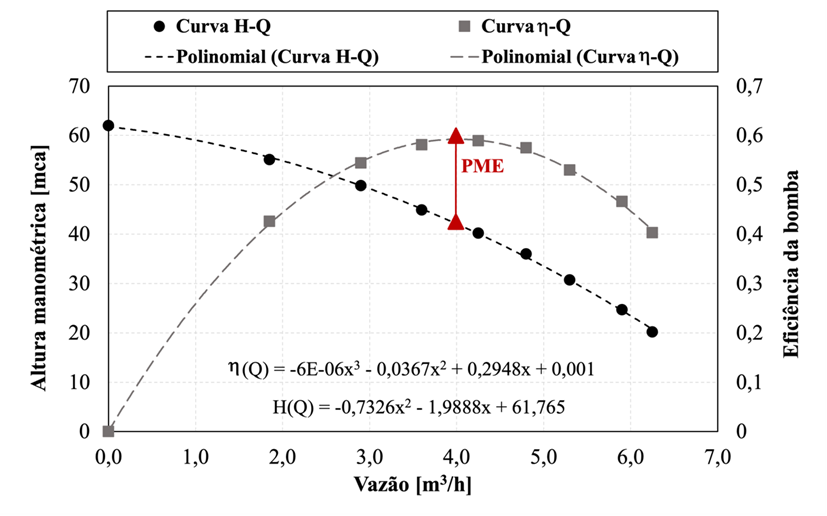
Fonte: Elaborado pelo autor.
- Gerador fotovoltaico SolarWorld SW245
O segundo GFV é da fabricante Solaris, composto por 20 módulos de modelo S55P, de potência nominal de 55 WP cada. Para suprir a demanda do DCP utilizado, foram necessários 18 módulos do gerador (Figura 3.2).
Figura 3.2 – Gerador fotovoltaico de 10 módulos SW245 da Solarworld.

Fonte: Elaborado pelo autor.
O gerador foi instalado em uma estrutura baseada em um telhado típico brasileiro, com suportes de alumínio e ferro. A estrutura é composta por hastes de alumínio, com o azimutal direcionado para o norte magnético, com inclinação de 14º. As informações dos parâmetros técnicos padrões de fábrica (STC) e medidos no laboratório, por intermédio do simulador Pasan Measurement Systems classe A+A+A+, estão destacados na Tabela 3.4.
Tabela 3.4 – Média dos parâmetros elétricos de cada módulo SW245.

Fonte: Elaborado pelo autor, adaptado de SolarWorld (2011).
3.3 Sistema fotovoltaico de bombeamento utilizado
O SFB utiliza um DCP diferente, um conversor de frequência (CF), o CFW-11, da fabricante WEG, com tensão de operação na faixa de 200-240 VCA, conectado a motobomba Leão 4R5PA. O CF não é um equipamento dedicado ao SFB, logo, não possui tecnologias de seguimento do ponto de máxima potência (SPMP).
Além disso, não há indicações da potência do GFV para suprir a motobomba por parte da fabricante. Em Alonso-Abela, Chenlo e Blanco (2002), citado por Santos (2016, p.63), é estimado que um GFV deva ter uma potência de pico nominal 1,15 vezes maior que a potência requerida pela motobomba para a frequência nominal. Ao estimar a potência requerida para o motor em 100 % de carregamento de 1050 W – considerando a potência nominal de 1 cv (735,5 W) e 70 % de eficiência nominal do motor – a potência do GFV deveria estar próxima a 1207,5 WP. No trabalho, devido a indisponibilidade de um gerador de potência próxima ao calculado, utilizou-se o GFV de 18 módulos S55P de potência máxima nominal de 990 WP.
Para suprir a tensão alternada do conversor de frequência, de 200-240 VCA, é solicitado VCC na faixa de 282-338 V (Silva, 2019). O CFW-11 suporta a tensão máxima de 400 VCC, com proteção de sobretensão acima desse valor. Dessa forma, o GFV tem uma tensão de máxima potência (VMP) na faixa de 327,6 V e tensão de circuito aberto (VOC) abaixo de 393,3 V, impedindo a atuação da falha de sobretensão no CFW-11, de 400 V. A eficiência do DCP é de 97 % de acordo com a fabricante (WEG S.A., 2020).
Embora já existam diversos modelos de CF convencional no mercado com essa funcionalidade, o CFW-11 tem como grande desvantagem a indisponibilidade do circuito de SPMP, que aumenta o rendimento de SFB. A partir desta situação, criaram-se estratégias para garantir um rendimento aceitável do CF e motobomba, seja por intermédio da criação de circuitos externos acoplados no CF, seja com parametrizações. Em Silva (2019), foi recorrido ao uso da estratégia de manter a tensão do barramento c.c. fixa, mediante o controle PID de malha fechada, semelhante ao que foi aplicado para o controle de pressão da bancada de ensaios. O controlador PID condiciona o motor de indução da motobomba para manter a estabilidade do sinal de referência, o set-point, regulando a sua frequência de rotação à medida que perturbações afetem o sistema. Isso é possível com o auxílio de uma realimentação no sistema de controle, como mostra a Figura 3.4. O PID mantém a tensão do barramento c.c. (variável de processo) próxima ao set-point configurado, através do sinal de realimentação, de modo a condicionar o erro próximo a zero.
Figura 3.3 – Diagrama de blocos simples do controlador PID de malha fechada.
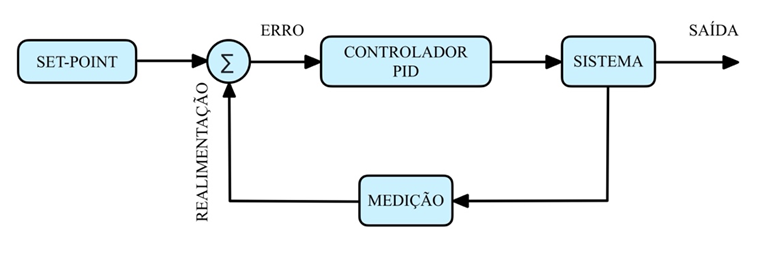
Fonte: Elaborado pelo autor.
A estratégia de fixar a tensão do barramento c.c. é simples, no entanto, devido a intermitência da irradiância e temperatura do módulo ao longo do dia, o SFB irá operar fora do ponto de máxima potência em muitos momentos do dia (Brito, 2006; Santos, 2016), diferente de um SPMP que constantemente atualiza o ponto de operação da curva I-V, como é retratada na Figura 3.4.
Figura 3.4 – Ação da tensão fixa com a variação do ponto de máxima potência do GFV em relação a irradiância (a) e temperatura (b).
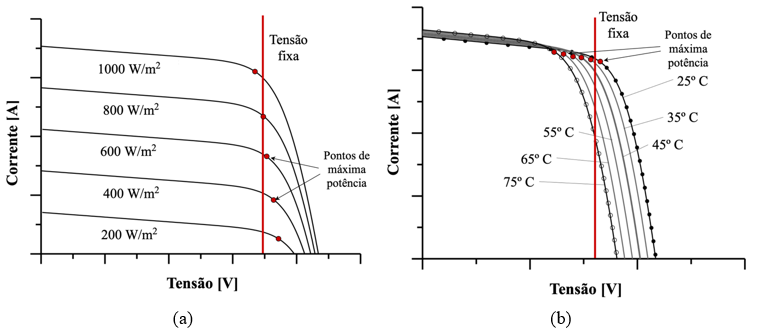
Fonte: Elaborado pelo autor.
De modo a diminuir esse efeito, é preciso utilizar níveis de tensão mais adequados para o bombeamento. Em Silva (2019), com o auxílio do gráfico de distribuição de energia da região de Belém, a faixa de tensão utilizada no GFV ficou entre 250-280 V. No entanto, embora sejam valores com maiores contribuições na produção de energia, são valores inferiores a faixa requerida para o CFW-11, logo, pode influenciar no desempenho do sistema.
A realimentação do sistema é adquirida por meio da tensão do GFV, limitada a uma faixa por um divisor de tensão para a entrada de realimentação do CF, de até 10 VCC. Ele possui dois resistores, um de 19,7 quilo Ohms (kW) e outro de 1 mega Ohms (MW), onde a tensão do primeiro irá ao CFW-11 e a tensão do somatório seguirá para o transdutor de tensão (Figura 3.5).
Figura 3.5 – Diagrama de realimentação do CFW-11 para o controle PID.
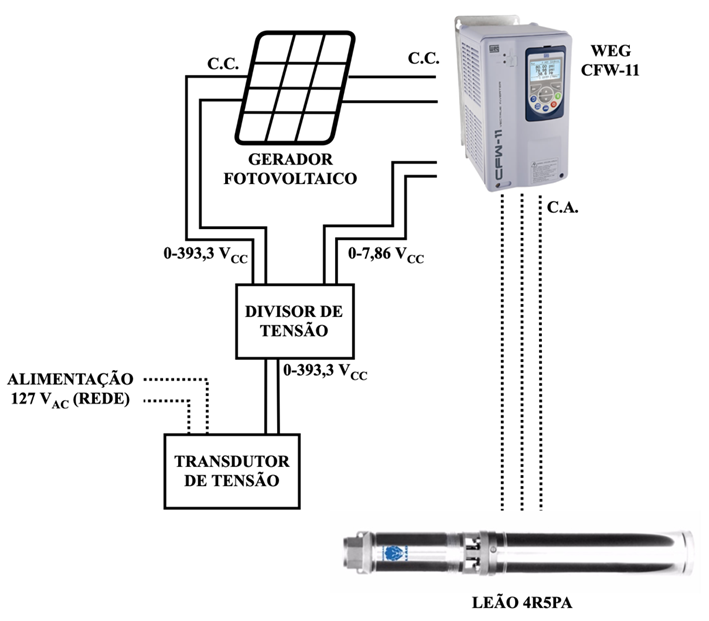
Fonte: Elaborado pelo autor.
4. RESULTADOS
A simulação de pressão da bancada de ensaios (ver Figura 4.1) é composta por um conversor de frequência convencional e uma motobomba de 3 cv, que utiliza um sistema de controle proporcional integral e derivativo para manter a pressão fixa em um valor determinado pelo usuário. Ela também apresenta um reservatório de água pequeno, para o reaproveitamento de água, e uma estrutura elaborada por perfis metálicos de alumínio, com suportes para os equipamentos de medição, de proteção, o sistema de tubulação que interconecta o sistema fotovoltaico de bombeamento e o simulador de pressão, e os DCP. Por ele, realizaram-se diversos ensaios na bancada, com simulações de 2 alturas manométricas, 20 e 40 metros de coluna d’água (mca), para observar os resultados do SFB.
Figura 4.1 – Bancada de ensaios.

Fonte: Elaborado pelo autor.
4.1. Metodologia aplicada
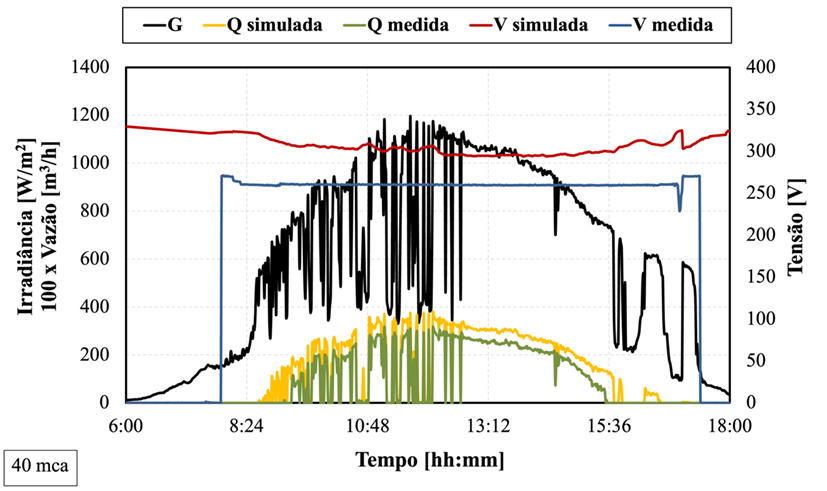
Na Figura 4.2 são apresentados os resultados da vazão, tanto medida quanto simulada, para as alturas manométricas de 20 e 40 mca. Respectivamente, os ensaios foram configurados para uma tensão fixa de 270 V e 260 V. Para H = 20 mca, observa-se que o início da vazão simulada precedeu o registrado no ensaio. Isso pode ser atribuído ao sombreamento ainda presente no GFV, o qual pode não ter sido detectado pela célula de referência.
Figura 4.2 – Comparação das potências e eficiências simuladas e medidas em 20 mca (a) em 45 mca (b).
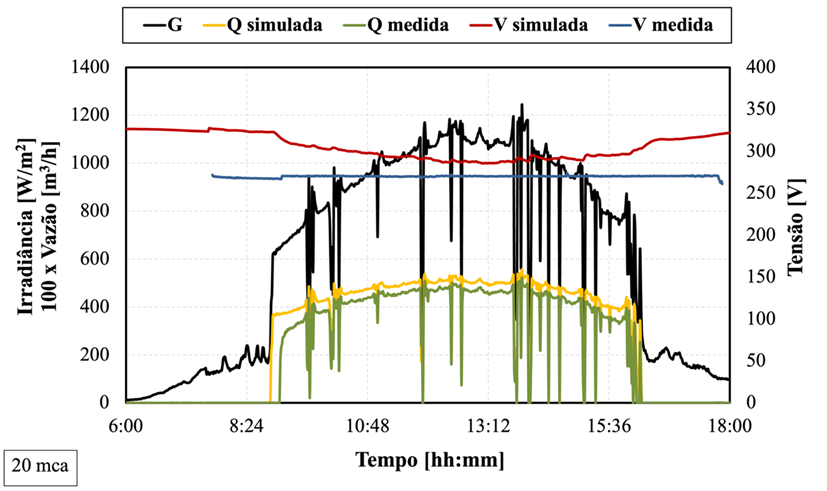
(a)
(b)
Fonte: Elaborada pelo autor.
Em ambos os casos há uma semelhança nos perfis de vazão, porém com uma diferença nos valores obtidos que pode ser atribuída ao sistema de controle de manter a tensão fixa na curva I-V do gerador por meio do CFW-11, o qual não é especificamente projetado para sistemas fotovoltaicos, logo, não possui uma configuração dedicada para o SPMP. Nesta situação, optou-se por empregar esse sistema de controle PID. Essa estratégia, embora simples, por buscar a otimização do desempenho do sistema sem recorrer a uma tecnologia destinada ao rastreamento do ponto da curva I-V do GFV, pode ser uma causa do menor desempenho da bomba.
A seleção da tensão do barramento c.c. foi baseada nos gráficos de distribuição de energia produzida em Belém-PA pelo gerador fotovoltaico, em função da sua tensão de máxima potência, conforme apresentado nos estudos de Silva (2019). A faixa de tensão indicada reflete os maiores níveis de potência acumulada ao longo das horas durante um ano típico, representando assim a faixa que melhor se adequa ao casamento de impedância entre a carga e a fonte geradora de energia elétrica (Brito, 2006). Segundo Silva (2019), no caso deste gerador fotovoltaico, a tensão deve ser mantida na faixa de 250 a 280 VCC.
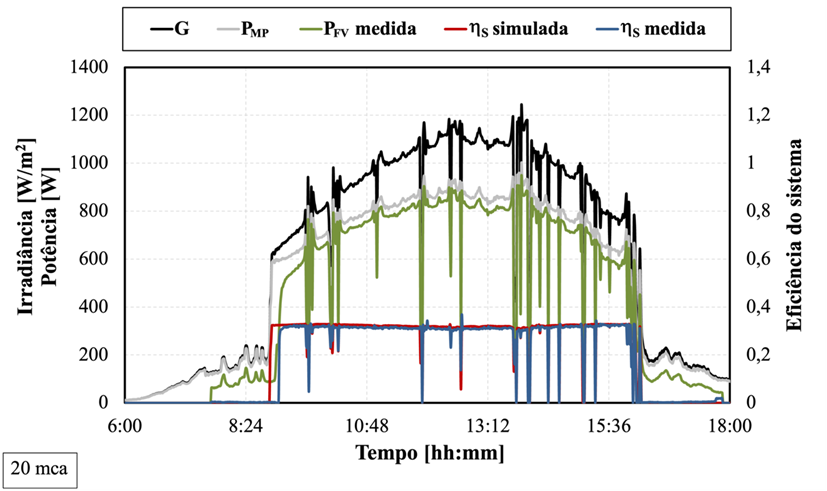
Utilizando a Figura 3.18 para exibir a comparação das potências do GFV e eficiências do sistema, percebe-se que no início e no fim da operação é onde há uma notável disparidade nos perfis de potência devido à diferença substancial na tensão do barramento c.c. Assim, em H = 20 mca, hSPMP está próximo a 57 % para níveis inferiores a 220 W/m2, e aumenta para 92 % quando ultrapassa 600 W/m2, com média de 89 %. Para 40 metros, a média de hSPMP do exemplo foi de 85 %.
Figura 4.3 – Comparação das potências e eficiências simuladas e medidas em 20 mca (a) em 45 mca (b).
(a)

(b)
Fonte: Elaborada pelo autor.
Como essa situação não é prevista na simulação deste trabalho, incrementa-se o erro final. Isso ocorre porque as fórmulas utilizadas para calcular a potência fotovoltaica na simulação assumem um DCP que busca constantemente atingir a máxima potência do gerador. No entanto, esse comportamento não é replicado no SFB com o CFW-11. Consequentemente, tanto a potência quanto a vazão simulada do SFB permaneceram mais elevadas em comparação com as medições realizadas.
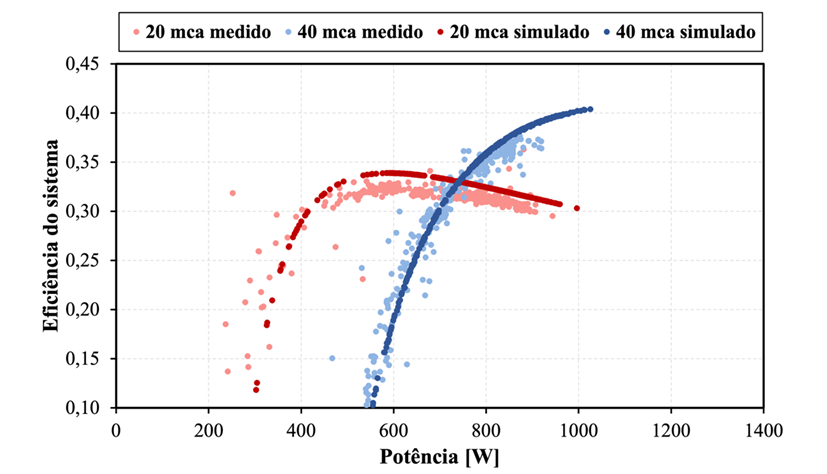
Em contrapartida, as eficiências do sistema, se mantiveram bastante semelhantes ao obtido com a simulação. A Figura 4.4 exibe a comparação das curvas de eficiência do sistema para ambas as alturas manométricas. Observa-se uma maior precisão na previsão em comparação com outros sistemas. Para 20 metros, há uma maior diferença entre as curvas hS, comparado com 40 metros. Com essa análise, fica evidente que a simulação foi capaz de fazer uma boa estimativa, com dados simulados alinhados aos medidos na bancada de testes.
Figura 4.4 – Curvas de eficiência do sistema no SFB 3.
Fonte: Elaborado pelo autor.
4.2. Aplicação da metodologia para obtenção do ponto de melhor eficiência solar
A região de Belém do Pará é caracterizada por três períodos: a época chuvosa, entre dezembro e maio; o período final chuvoso, entre junho e agosto; e a fase de estiagem, entre setembro e novembro, a qual há diminuição da frequência de chuvas (Bastos et al., 2002). Essa característica afeta o valor do PMES, pois será diferente a cada dia, mesmo com irradiações semelhantes, por conta dos perfis específicos, influenciam o PMES do SFB.
De acordo com o programa SunData v3.0, desenvolvido pelo Laboratório de Modelagem e Estudos de Recursos Renováveis de Energia (LABREN), uma das divisões do Instituto Nacional de Pesquisas Especiais (INPE), baseado no trabalho de Pereira et al. (2017), a média anual da irradiação diária para a localidade é de 4,86 kWh/m2 (ou 4,86 horas de sol pleno – HSP), com a máxima em setembro (5,38 HSP) e a mínima durante fevereiro (4,40 HSP). Assim, este estudo utilizou dados de 10 dias com irradiações diárias entre a mínima (4,40 kWh/m2) e a máxima (5,38 kWh/m2). Através do simulador, foram obtidas as informações do PMES, eficiência do sistema e o volume acumulado. Ao final, foi calculada uma média dos 10 dias para determinar o PMES para os sistemas fotovoltaicos de bombeamento. Os dados utilizados variaram de 4,42 até 5,30 kWh/m2, apresentando uma média de 4,96 HSP.
A Tabela 4.1 compila as simulações realizadas para o SFB. Com dados de 10 dias, o sistema demonstrou um PMES médio de 22,3 metros de coluna d’água. Ao comparar com a altura manométrica do PME nominal (HPME), que é de 41,9 mca, observa-se uma diminuição em cerca de 20 metros na profundidade de instalação da bomba.
Tabela 4.1 – Valores de PMES para o SFB 3.

Fonte: Elaborado pelo autor.
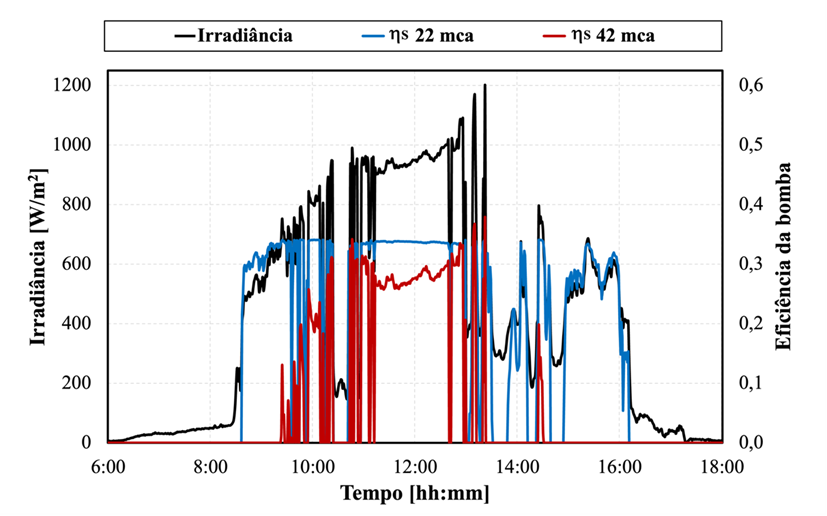
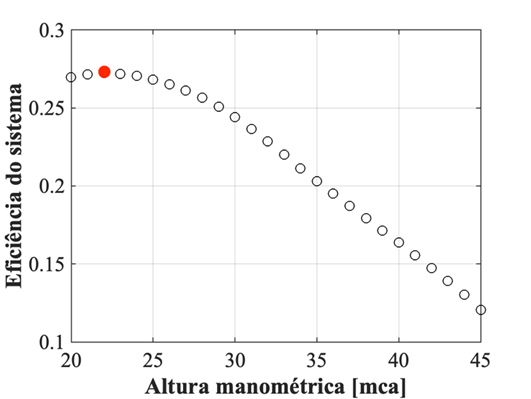
No cenário do dia 3, que registrou irradiação diária mais próxima da média anual, foram elaborados gráficos como base para a análise do SFB 3. A Figura 4.5 ilustra a comparação entre o PMES e o PME para esse dia. Considerou-se 22 mca para a média de PMES e 42 mca para o PME na simulação. Fica nítido uma discrepância na eficiência do sistema ao longo do dia, dado que a motobomba não recebe potência suficiente para operar em 42 mca.
Com isso, há apenas alguns momentos em que a eficiência do PME supera a do PMES, durante os picos de irradiância. Na parte da tarde, exceto por um breve período, não houve uma operação eficaz com a altura manométrica de 42 mca. Através da análise da comparação das eficiências do sistema para H = {20:1:45} no dia 3 (Figura 4.6b), é evidenciado que uma instalação da motobomba em uma altura manométrica próxima à nominal resultaria em uma acentuada queda de eficiência no sistema.
Figura 4.5 – Gráfico de irradiância e hS em 22 e 42 mca no dia 3 (a); Eficiências do sistema para H = {20:1:45} no dia 3 (b).
(a)
Fonte: Elaborada pelo autor.
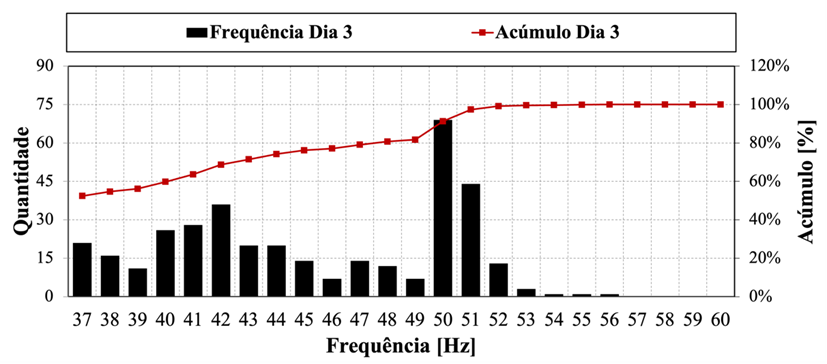
Para que a bomba inicie o deslocamento de água em HPME, é necessário alcançar cerca de 650 W/m2 no GFV. Já para HPMES, a irradiância deve ser superior a 350 W/m2. Assim, para esse cenário, é destacada a importância de avaliar cautelosamente as condições de operação que a bomba deve atuar, para evitar grandes perdas de energia. A Figura 4.6 apresenta as faixas de frequência de operação para o dia 3. Com base na simulação deste dia, verificou-se que a bomba não conseguiu atuar em 60 Hz, atingindo o máximo em 56 Hz. A operação da bomba a 22 mca se concentrou principalmente na faixa entre 37-52 Hz, , sendo que mais de 90% do volume bombeado se encontra em frequências menores ou iguais a 50 Hz.
Figura 4.6 – Distribuição de faixas de frequências para o PMES do dia 3.
Fonte: Elaborado pelo autor.
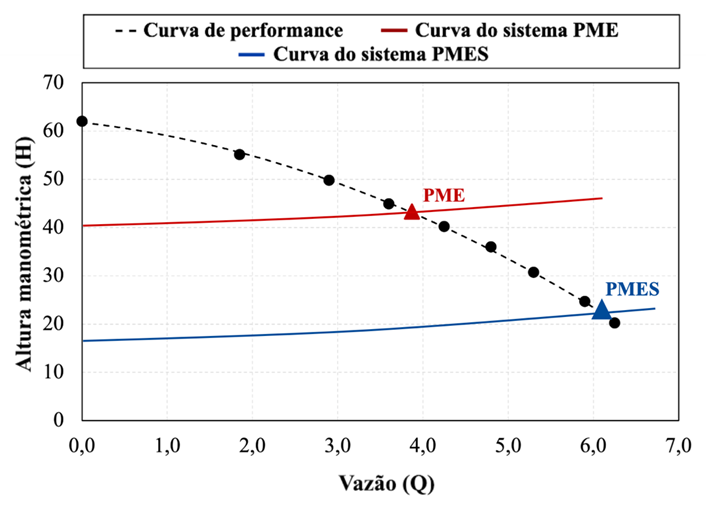
Dessa forma, conclui-se que o gerador S55P de 970 WP não possuiu potência suficiente para alcançar a produção da bomba em frequência nominal. Esse cenário teve um impacto direto na alteração do PMES, resultando em uma queda de cerca de 20 metros de coluna d’água em relação ao HPME (Figura 4.8).
Figura 4.7 – Curvas do sistema do PMES e PME para o SFB 3.
Fonte: Elaborado pelo autor.
No entanto, devido à restrição de modelos disponíveis no laboratório, não foi viável integrar outros módulos ao GFV, uma vez que a alta tensão de circuito aberto ultrapassaria a capacidade máxima suportada pelo conversor de frequência (CF) de 400 V, gerando falhas constantes no sistema e inviabilizando o início de operação do SFB. A partir da situação apresentada, caso esse sistema estivesse operando no PME, tornar-se-ia claro o prejudicamento substancial do desempenho, resultando em baixa eficiência e uma produção de água insuficiente para atender às demandas de uma comunidade, como evidenciado na Figura 4.8.
Figura 4.8 – Comparação de eficiência do sistema e volume acumulado do PMES do SFB 3.
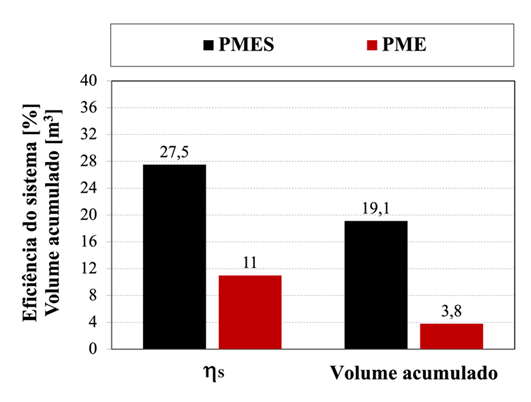
Na simulação com a adoção do PMES de 22 mca para a simulação, resultou-se em um acúmulo médio de água de 19,1 metros cúbicos (m3), o que corresponde a 19.100 litros. Por outro lado, o PME de 42 mca registrou apenas 3.800 litros, quase 20 % com o obtido pelo HPMES, e com uma eficiência de sistema menor que a metade da adquirida com 22 mca.
Devido à utilização de um gerador fotovoltaico de menor potência, era prevista uma diminuição do ponto de operação ideal para a bomba. Assim, de forma a otimizar o desempenho desse sistema, deve-se posicionar a motobomba em uma altura manométrica muito próxima ao mínimo suportado pela bomba Leão 4R5PA. Dessa forma, viabilizaria a extração do máximo desempenho, promovendo uma operação mais eficaz e econômica para atender às necessidades de uma comunidade de forma adequada.
CONCLUSÃO/CONSIDERAÇÕES FINAIS
Esse estudo trouxe uma discussão sobre a validação da metodologia para a aquisição do ponto máximo de eficiência solar. A obtenção de dados precisos sobre o sistema é essencial para garantir a confiabilidade do programa. No entanto, devido a constante indisponibilidade pública das informações detalhadas os componentes do SFB, a utilização de valores teóricos, provenientes de fontes bibliográficas, demonstrou ser uma alternativa válida. Com essa técnica, as curvas de eficiência apresentaram uma proximidade considerável, e que reforçou a confiabilidade dos resultados discutidos no estudo. Em situações que demandam maior precisão, a obtenção das curvas reais dos componentes seria a abordagem mais indicada para aprimorar a precisão dos pontos de operação calculados pelo Matlab.
Todavia, mesmo com a semelhança das curvas de eficiência, entendeu-se que, em muitos casos, a simulação não reflete fielmente a realidade do SFB. Os cálculos analíticos utilizam equações que consideram uma operação teórica sistema, e não as possíveis influências do controle feito pelo DCP. Mesmo assim, a metodologia demonstrou uma capacidade notável em prever os desempenhos na entrega de vazão pela bomba, assemelhando-se em muitos casos à realidade. Isso a posiciona como uma opção viável para determinar um ponto de operação mais otimizado para o sistema fotovoltaico de bombeamento.
Em um projeto de instalação da bomba, seria mais benéfico para a população ajustar o ponto de operação próximo ao PMES determinado pelo gerador fotovoltaico. Em situações em que a produção de água com o PME já seria o suficiente para atender à demanda, e o seu aumento com o uso do PMES resultaria em desperdício de água, a estratégia mais interessante seria permutar o uso do GFV com outras necessidades da população ou mesmo projetar uma bomba de menor potência e reduzir a quantidade de módulos do gerador, visando maximizar a economia de energia sem comprometer a produção de água.
Portanto, esse estudo presenciou a relevância da utilização desta metodologia e observou que, não apenas para garantir a eficiência energética, mas também as necessidades específicas de uma comunidade, a determinação do PMES surge como uma valiosa técnica para aprimorar o desempenho dos SFB. Esta pesquisa contribui, com algumas aplicações práticas e teóricas, com o objetivo de incluir soluções sustentáveis para o acesso à água potável de forma eficiente e econômica para populações remotas e com recursos limitados.
REFERÊNCIAS
ALONSO-ABELA, M.; CHENLO, F.; BLANCO, J. Optimización del Uso de Convertidores de Frecuencia con Bombas Centrífugas y Motores Trifásicos en Sistemas de Bombeo Fotovoltaico. Era Solar: Energías Renovables, n. 2, p. 14-35. 2002.
BASTOS; T. X.; PACHECO, N. A.; NECHET, D.; SÁ, T. D. DE A. Aspectos climáticos de Belém nos últimos cem anos. Belém. Embrapa Amazônia Oriental. 2002. 31p.
BORDALO, C. A. L. Pelo direito humano ao acesso à água potável na região das águas: uma análise da exclusão e do déficit dos serviços de abastecimento de água potável à população da Amazônia brasileira. Novos Cadernos NAEA, v. 25, n. 1, 2022.
BRASIL. Lei No 11.445, de 5 de janeiro de 2007. Estabelece diretrizes nacionais para o saneamento básico e dá outras providências. Brasília, DF. Diário Oficial da União. 2007.
BRITO, A. U. Otimização do Acoplamento de Geradores Fotovoltaicos a Motores de Corrente Alternada Através de Conversores de Frequência Comerciais para Acionar Bombas Centrífugas. 2006. 83p. Tese de Doutorado – Programa Interunidades de Pós-Graduação em Energia, Universidade de São Paulo, São Paulo.
BURT, C. M.; PIAO, X.; GAUDI, F.; BUSCH, B.; TAUFIK, N. F. N. Electric motor efficiency under variable frequencies and loads. Journal of Irrigation and Drainage Engineering, v. 134, n. 2, p. 129-136. Março/ abril 2008.
FRANKLIN ELECTRIC S.A. Motores Submersos 4”: Uma nova geração de soluções para bombeamento de águas subterrâneas. Franklin Electric Indústria de Motobombas S.A. Joinville. 2015. Disponível em: https://schneidermotobombas.blob.core.windows.net/media/204807/manual-motores-aim.pdf. Acesso em: 16 out. 2023.
HSU, J. S.; KUECK, J. D.; OLSZEWSKI, M.; CASADA, D. A.; OTADUY, P. J.; TOLBERT, L. M. Comparison of induction motor field efficiency evaluation methods. Conference Record of the 1996 IEEE Industry Applications Conference Thirty-First IAS Annual Meeting. IEEE. p. 703-712. 1996.
KARASSIK, I. J.; MESSINA, J. P.; COOPER, P.; HEALD, C. C. Pump handbook. 3a Ed. New York: McGraw-Hill, 2001.
LEÃO S.A. Tabela de Curvas Características 60Hz. Joinville. Leão S.A. 2023. Disponível em: https://bombasleao.blob.core.windows.net/media/302416/leao_lista_curvas_60hz_2023_web.pdf. Acesso em 16 out. 2023.
MACÊDO, W. N. Análise do Fator de Dimensionamento do Inversor aplicado a
Sistemas Fotovoltaicos Conectados à Rede. 2004. 183p. Tese de Doutorado. Programa Interunidades de Pós-Graduação em Energia – Universidade de São Paulo, São Paulo.
MACINTYRE, A. Bombas e Instalações de Bombeamento. 2a Ed. LTC, Rio de Janeiro, 1997.
MCCOY, G.A.; DOUGLASS, J. G. Premium Efficiency Motor Selection and Application Guide. Washington, U. S. Department of Energy (U.S. DOE). 2014. Disponível em: https://www.energy.gov/eere/amo/articles/premium-efficiency-motor-selection-and-application-guide-handbook-industry. Acesso em: 16 out. 2023.
MORALES, L. R. V. Sistemas fotovoltaicos de bombeamento com conversores de frequência e motobombas de fabricação nacional: avaliação e orientações para sua implantação. 2016. 143p. Tese de Doutorado – Programa de Pós-Graduação em Energia, Universidade de São Paulo, São Paulo.
MUÑOZ, J.; CARRILLO J. M.; MARTÍNEZ-MORENO, F.; CARRASCO, L. M.; NARVARTE, L. Modeling and simulation of large PV pumping systems. Proceedings of the 31th European Photovoltaic Solar Energy Conference and Exhibition, Hamburg. 2015.
NATURAL RESOURCES OF CANADA/ RESSOURCES NATURELLES CANADA. Energy-Efficient Motor Systems: Assessment Guide. Ottawa. NRC. 2004b. Disponível em: https://publications.gc.ca/site/eng/290084/publication.html. Acesso em: 16 out. 2023.
PEREIRA, P.F.; SOUZA, A.C.; SANTOS, I.N. Modelagem e Avaliação de Desempenho das Principais Técnicas de Controle de MPPT Empregadas na Geração Fotovoltaica. XVI CEEL. Uberlândia. Outubro de 2016. Disponível em: https://www.peteletricaufu.com.br/static/ceel/doc/artigos/artigos2016/ceel2016_artigo012_r01.pdf. Acesso em: 16 out. 2023.
PINHO, J. T.; GALDINO, M. A. Manual de Engenharia para sistemas fotovoltaicos. 2014.
PINHO, J. T. et al. Sistemas híbridos: Soluções Energéticas para a Amazônia. Brasília: Ministério de Minas e Energia, 2008.
RIVALIN, L.; PRITONI, M.; STABAT, P.; MARCHIO, D. Adaptation of fan motor and VFD efficiency correlations using Bayesian inference. Science and Technology for the Built Environment, v. 25, n. 7, p. 836-848. 2019.
SANTOS, W. S. dos. Modelagem e de Desenvolvimento de um Conversor de Frequência Aplicado à Sistemas Fotovoltaicos de Bombeamento de Água. 2022. 174p. Tese de Doutorado – Programa de Pós-graduação em Engenharia Elétrica, Universidade Federal do Pará, Belém.
SCHMIDT, H.; JANTSCH, M.; SCHMID, J. Results of the concerted action on Power conditioning and control. EUROPEAN PHOTOVOLTAIC SOLAR ENERGY CONFERENCE, 1992, Montreux, Switzeland. Proceedings. Montreux, 1992.
SILVA, G. B. de S. Ensaios de Sistemas Fotovoltaicos de Bombeamento Mediante Simulação de Alturas Manométricas em uma Bancada. 2019. 95p. Trabalho de Conclusão de Curso – Faculdade de Engenharia Elétrica e Biomédica, Universidade Federal do Pará, Belém.
SOLARWORLD. SW 245 poly/ Version 2.0 and 2.5 Frame. [s.l.]. 2011. Disponível em: https://s3.amazonaws.com/ecodirect_docs/SOLARWORLD/SW245_Poly.pdf. Acesso em: 16 out. 2023.
SOUZA, C. M. N.; NOGUEIRA, A. S.; VASCONCELOS, A. S. da S.; SILVA, A. de S. Abastecimento de água em comunidades ribeirinhas da Amazônia brasileira e promoção da saúde: análise de modelo de intervenção e de gestão. Novos Cadernos NAEA, v. 15, n. 2, 2013.
ULANICKI, B.; KAHLER, J.; COULBECK, B. Modeling the efficiency and power characteristics of a pump group. Journal of water resources planning and management, v. 134, n. 1, p. 88-93. 2008.
WORLD BANK GROUP. Solar Pumping: The Basics. World Bank, 2018.
Gabriel Bastos de Souza Silva – Discente do Curso de Pós-Graduação de Engenharia Elétrica do Instituto de Tecnologia na Universidade Federal do Pará. e-mail: gabrielbssilva1@gmail.com1
Wanderley Sena dos Santos – Discente do Curso de Pós-Graduação de Engenharia Elétrica do Instituto de Tecnologia na Universidade Federal do Pará. Doutor em Sistemas de Energia. e-mail: wsenasantos@gmail.com2
Wilson Negrão Macêdo – Docente do Curso de Pós-Graduação em Engenharia Elétrica do Instituto de Tecnologia na Universidade Federal do Pará. Doutor em Sistemas de Energia (PPGEE/UFPA). e-mail: wnmacedo@ufpa.br3
