MODELAGEM DE DADOS DE FALHAS EM UMA MÁQUINA DOBRADEIRA E DE CORTE A LASER DE UMA INDÚSTRIA FABRICANTE DE EQUIPAMENTOS DE COZINHA INDUSTRIAL
REGISTRO DOI:10.5281/zenodo.10202246
Felipe Rodrigues de Souza1
Guilherme Toledo Robbi Melim2
Mardy Wilian Souza da Silva3
Ruhan Vinícius Ribeiro4
Vinicius de Godoy Curi5
Guilherme Henrique da Silva Lázaro6
Caroline Martins Fraga de Melo7
Renato Cardoso Tudela8
Resumo
Este estudo apresenta uma análise de falhas em máquinas industriais de uma empresa especializada em fabricação de equipamentos para cozinhas industriais. Em um mercado altamente competitivo, a gestão eficaz de manutenção é crucial para garantir que os equipamentos operem com alta disponibilidade e confiabilidade. Este contexto inicia a pesquisa, destacando a importância da gestão de manutenção em face das demandas crescentes por desempenho e eficiência. O estudo de caso reúne dados detalhados de falhas do maquinário, utilizando o software ProConf 2000 para modelar o tempo até a ocorrência dessas falhas. Para encontrar a distribuição mais adequada que descreva esses dados, foram aplicados métodos analíticos e gráficos. A pesquisa destaca a importância de monitorar e gerenciar de perto o desempenho das máquinas, a fim de maximizar sua vida útil e minimizar paralisações não programadas.
Palavras-chave: Gestão de Manutenção, Análise de Falhas, Confiabilidade.
1 INTRODUÇÃO
A economia e o mercado cada vez mais globalizado, tem exigido e forçado as empresas a serem mais competitivas, preparando-se para frequentes mudanças que tragam economia, bem como buscar diferenciais em sua produção. Diante desse cenário as organizações necessitam de equipamentos com alta disponibilidade e confiabilidade (ANDRADE; MACIEL, 2021).
Cada vez mais há procura por equipamentos que possam oferecer mais segurança em relação a disponibilidade e baixa taxa de falhas, pois há menor custo de manutenção, o que acaba sendo um bom investimento. A falha em equipamentos pode gerar problemas em várias escalas, de pequenas inconveniências a grandes impactos no mercado. Portanto, o estudo da confiabilidade é muito importante para garantir a segurança da produção e da comercialização de um produto durante o tempo de uso, já que no mercado não é esperado falhas em seu processo produtivo (SELLITTO, 2007).
O estudo de confiabilidade tem grande relevância para a manutenção já que apresenta constantemente uma maior confiabilidade de um equipamento. Quanto maior a confiabilidade há a confirmação de que a manutenção está sendo executada de maneira eficaz, bem como se espera menores tempos nos reparos dos equipamentos e consequentemente maiores tempos destinados à produção e maior qualidade dos produtos. (FOGLIATTO; RIBEIRO, 2009).
Foi na Primeira Guerra Mundial que surgiu o estudo da confiabilidade, sendo utilizado para descrever estudos comparativos feitos em aviões com um, dois ou quatro motores e teve avanços pelas indústrias bélicas durante e após a Segunda Guerra Mundial, na qual permitiram o amadurecimento e ampliação da teoria. De acordo com Fogliatto e Ribeiro (2009) a partir de 1970 este conceito vem sendo aplicado nas mais diversas áreas.
Equipamentos que recebem manutenção adequada garantem elevados padrões, custos operacionais baixos, já que se tem uma produção segura e ciclo de vida do equipamento elevado, devido à preservação do mesmo (BRANDÃO; ANDRADE, 2018).
Baseando-se na análise de dados históricos, a confiabilidade é uma medida fundamental utilizando distribuições de probabilidade e ferramentas de modelagem de software e concentra nos intervalos entre falhas e desempenha um papel central na área de estudos de confiabilidade (FOGLIATTO; RIBEIRO, 2009).
Para calcular a confiabilidade de um sistema é crucial entender a distribuição de probabilidade que melhor descreve os tempos entre falhas. Isso envolve o uso de técnicas estatísticas avançadas para modelar o comportamento desses tempos, permitindo que as organizações otimizem a manutenção, reduzam o tempo de inatividade e potencializam a eficiência operacional (BRANDÃO; ANDRADE, 2018).
O estudo de casos desempenha um papel importante na área de confiabilidade, fornece informações concretas e práticas sobre como aplicar os conceitos teóricos e as técnicas de análise em situações do mundo real, bem como ajudam a validar as abordagens de modelagem de confiabilidade e identificar áreas que podem precisar de melhorias e refinamentos (FOGLIATTO; RIBEIRO, 2009).
É levado em consideração nos estudos, fatores como o tempo médio entre falhas (MTBF) e o tempo médio de reparo (MTTR), a identificação de modos de falha, análise de causa raiz e a implementação de estratégias de manutenção preditiva, preventiva e corretiva. Com base nesses resultados, as organizações tomam decisões sobre como otimizar a confiabilidade de seus sistemas e reduzir o tempo de inatividade não planejado. Podem também destacar a importância da gestão de ativos e da adoção de práticas de manutenção baseadas em dados. Eles oferecem exemplos práticos de como a análise de confiabilidade pode impactar positivamente a eficiência operacional, a segurança e a satisfação do cliente (FOGLIATTO; RIBEIRO, 2009).
A proposta deste artigo tem como objetivo analisar os dados de falha e propor modelagens matemáticas para previsão e orientação quanto às manutenções preventivas, será apresentado o tempo até a falha e reparo, indicador de falha, disponibilidade e confiabilidade.
2 FUNDAMENTAÇÃO TEÓRICA
2.1Tempo até a falha e reparo
O “tempo até a falha de uma unidade” refere-se ao período desde o início da operação da unidade até a ocorrência de sua primeira falha (FOGLIATTO; RIBEIRO, 2009).
Inicialmente, o momento de início da operação é definido como t = 0. Devido a flutuações imprevisíveis, o tempo até a falha é tratado como uma variável aleatória, chamada de T (FOGLIATTO; RIBEIRO, 2009).
O estado da unidade em qualquer momento t é representado por uma variável de estado X(t), que é uma variável aleatória com dois estados possíveis: X(t) = 1, quando a unidade está operacional nesse momento, e X(t) = 0, quando a unidade não está operacional nesse momento.(KARDEC; NASCIF, 2009).
2.2Indicador de falha: tempo médio até a falha e até o reparo
A confiabilidade desempenha um papel central na engenharia mecânica, especialmente na busca por sistemas e componentes duráveis e eficientes. Neste contexto, destacam-se dois indicadores fundamentais: o MTTF (Tempo Médio até a Falha) e o MTTR (Tempo Médio até o Reparo). Esta seção se propõe a fornecer uma análise aprofundada desses indicadores, destacando suas fórmulas de cálculo e a importância de sua aplicação na engenharia mecânica. (KARDEC; NASCIF, 2009).
2.2.1MTTF (Mean Time to Failure, do inglês: Tempo Médio até a Falha)
Segundo Sellitto (2007), o MTTF representa a estimativa do período médio de operação de um componente ou sistema até que ocorra uma falha. Essa métrica é de suma relevância no contexto de engenharia mecânica, pois fornece uma perspectiva sobre a vida útil antecipada de um componente. A fórmula que governa o cálculo do MTTF é definida como:
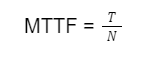
Onde:
– MTTF é o Tempo Médio até a Falha.
– T denota o tempo total de operação do componente ou sistema.
– N é o número de incidentes de falha observados durante esse intervalo.
2.2.3 MTTR (Mean Time to Repair, do inglês: Tempo Médio até o Reparo)
Segundo Sellitto (2007), o MTTR, por sua vez, é o período médio necessário para realizar a restauração de um sistema ou componente após a ocorrência de uma falha. Na esfera da engenharia mecânica, essa métrica desempenha um papel crucial, impactando diretamente o tempo de inatividade não programado. A fórmula subjacente ao cálculo do MTTR é expressa da seguinte maneira:
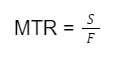
Onde:
– MTTR é o Tempo Médio até o Reparo.
– S representa o tempo total dedicado ao serviço, excluindo o tempo de falha.
– F é o número de incidentes de falha registrados.
2.3 Disponibilidade
A disponibilidade, em um contexto industrial e de engenharia, é uma métrica que mede a capacidade de um sistema, equipamento, máquina ou processo de estar operacional e pronto para executar suas funções quando necessário, ou seja, disponível para uso. Ela representa a porcentagem de tempo em que um ativo está em pleno funcionamento e pode ser utilizado efetivamente, sem interrupções não planejadas, devido a falhas ou manutenções corretivas (SELLITTO, 2007).
A disponibilidade inerente é uma medida que se concentra exclusivamente no tempo de reparo de um equipamento ou sistema, excluindo outros tempos associados, como logística, deslocamentos, entre outros. Ela representa a porcentagem de tempo em que o equipamento estaria disponível se não houvesse perdas de tempo ou atrasos, ou seja, se apenas o tempo de reparo fosse considerado (SELLITTO, 2007).
É definida pela fórmula:
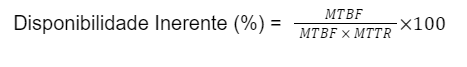
• O termo ‘’Inerente’’ (ou intrínseco) relaciona-se com o fato de no MTTR estar levando em conta somente tempo de reparo em manutenções corretivas, excluindo-se todos os demais tempos (Lógica, espera, sobressalentes, deslocamentos, etc.)
Onde:
•MTBF = Tempo médio entre falhas:
É uma medida básica de confiabilidade de itens reparáveis. Aplicável à manutenção corretiva
•MTTR = Tempo médio para reparo
É uma média dos tempos utilizados exclusivamente para os reparos corretivos (não leva em conta tempos de logística, preparação, espera de peças, etc.)
2.4 Confiabilidade
Segundo a NBR 5462, a confiabilidade de um item pode ser definida como a probabilidade do mesmo desempenhar o seu papel de acordo com o projetado por certo período de tempo e em determinadas condições de uso. Vale ressaltar, que o termo “confiabilidade” é usado como uma medida de desempenho de confiabilidade.
Tende-se a confundir os termos de Qualidade e Confiabilidade, Fogliatto (2009) diz que a principal diferença entre esses dois conceitos é que a confiabilidade incorpora a passagem do tempo; o mesmo não ocorre com a qualidade, que consiste em uma descrição estática de um item.
Abaixo, discutiremos as principais modelagens de distribuição de confiabilidade. (RIBEIRO,2007).
2.4.1. Distribuição Weibull
A distribuição de Weibull foi proposta originalmente por Weibull (1939) e sua ampla aplicabilidade foi também discutida por este mesmo autor (Weibull, 1951, 1954). Desde então, a mesma vem sendo frequentemente usada em estudos biomédicos e industriais. A sua popularidade em aplicações práticas formas, todas com uma propriedade básica: a sua função de taxa de falha ́ e monótona, isto é, ela é crescente, decrescente ou constante (FREITAS, COLOSSIMO; 1997).
Para Fogliatto (2009), é uma das distribuições mais importantes na modelagem de confiabilidade devido à sua flexibilidade e capacidade de representação de amostras de tempos até falha com comportamentos distintos. Na análise de amostras de tempos até falha de tamanho pequeno, supor dados seguindo uma distribuição de Weibull costuma ser um bom ponto de partida na análise.
Por consequência de se tratar de uma modelagem dependente de dois ou três parâmetros, a distribuição de Weibull modela adequadamente uma ampla variedade de situações em que unidades apresentam funções de risco distintas (FOGLIATTO, FLÁVIO; 2009). Estes parâmetros podem ser definidos como:
α – É o parâmetro de escala, conhecido como vida característica. Corresponde ao valor de t no qual existe aproximadamente 63.2% de probabilidade do que o componente venha a falhar.
y – É o parâmetro de forma, indica o comportamento da função da taxa de falha. Para y = 1, a função taxa de falha é constante (e equivale a distribuição exponencial). Para y > 1, a função taxa de falha é crescente, e quanto maior é este, mais rapidamente a função cresce. Para y < 1, a função taxa de falha é decrescente, e quanto menor é este, mais rapidamente a função decresce.
t0 – É chamado de tempo de falhas livre, parâmetro de localização ou vida mínima e indica a data de início das falhas.
As representações de confiabilidade da Weibull, para t ≥ 0, γ > 0 e > 0, são fornecidas nas seguintes equações:
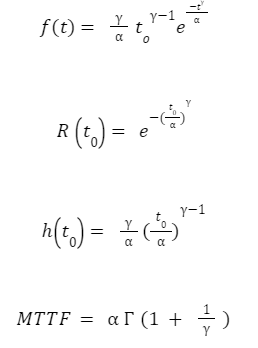
Sendo Gama :
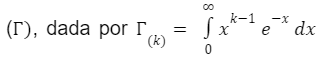
realizando as substituições devidas nas fórmulas mencionadas, é possível acharmos a Taxa de Falha da Distribuição de Weibull (FREITAS, COLOSSIMO; 1997).
Distribuição exponencial
Se trata da única distribuição contínua com função de risco constante, logo é tratada com uma das modelagens mais importantes nos estudos de confiabilidade. (FREITAS, COLOSSIMO; 1997).
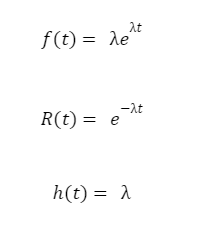
DISTRIBUIÇÃO LOGNORMAL
Segundo Colissimo (1997), Assim como a distribuição de Weibull, a distribuição log-normal é muito utilizada para caracterizar tempos de vida de produtos e indivíduos. Isto inclui fadiga de metal, semicondutores, diodos e isolação elétrica.
Ela também é bastante utilizada para descrever situações, como o tempo de vida de pacientes com leucemia. (GREGÓRIO; SILVEIRA, 2018)
As medidas de confiabilidade de interesse para a distribuição lognormal são (t ≥ 0):
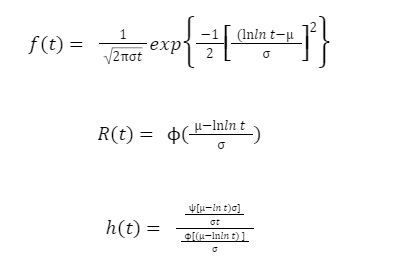
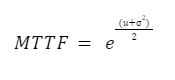
DISTRIBUIÇÃO NORMAL
A distribuição normal é comumente utilizada para análise de confiabilidade geral, tempos até a falha de componentes eletrônicos e mecânicos simples, equipamentos ou sistemas (LEWIS, 1987).
Para Lewis (1987), esta distribuição representa equipamentos que sofrem desgaste crescente, de forma que a taxa de falha apresenta uma curva crescente em função do tempo. Esta distribuição pode ser verificada quando se observa o comportamento da vida de ferramentas de corte durante a usinagem. (LEWIS, 1987).
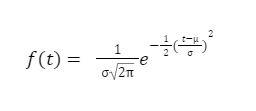
- MATERIAIS E MÉTODOS
3.4 ESTUDO DE CASO
Este estudo foi conduzido com base na provisão de dados provenientes de uma empresa especializada na produção de equipamentos e sistemas destinados às cozinhas profissionais, direcionando-se especificamente para redes de food’s service (do inglês: serviço de alimentação), gastronomia de alto padrão e estabelecimentos hoteleiros. A companhia, que tem uma história de aproximadamente meio século de existência, dedica-se a atender as demandas do mercado latino-americano e, no momento, dispõe de duas instalações fabris para garantir a satisfação das exigências do setor.
Apesar do notável porte da empresa e da sua longa trajetória no mercado, constatou-se a ausência de um plano de manutenção ideal. Como resultado, a organização tem recorrido frequentemente à manutenção corretiva, o que tem ocasionado perda de eficiência nos seus sistemas de produção.
- DADOS DE FALHA E REPARO
Para realização da análise, foram selecionadas três máquinas empregadas no âmbito do setor produtivo: uma dobradeira e um equipamento de corte a laser. Elas foram acompanhadas durante o período de um mês, no qual se registrou um total de dezessete falhas.
A partir da consolidação dos dados de falhas, foi utilizado o software ProConf, um programa computacional, desenvolvido pela Universidade Federal do Rio Grande do Sul (UFRGS), projetado para o ajuste de distribuições de tempos de falha para dados de confiabilidade, através do uso de métodos analíticos e métodos gráficos aplicando uma modelagem matemática que melhor se adequasse às incidências das ocorrências nos referidos equipamentos. Isso possibilitou a determinação de parâmetros essenciais, tais como confiabilidade, MTTF e MTTR.
Tabela 1 – Dados de falha
Fonte: os autores
- RESULTADOS E DISCUSSÃO
Após a conclusão do processamento de dados por meio do software ProConf 2000, foram extraídas informações de cada máquina. A seguir, serão apresentados os dados mais relevantes, detalhando os resultados obtidos para cada unidade de processamento.
4.1 DOBRADEIRA
No início, foram gerados gráficos que dizem respeito ao conjunto de dados relacionados ao tempo até que a máquina apresentasse falhas. A Figura 1 exibe como essas falhas ocorreram com o passar do tempo, mostrando o número de falhas em diferentes intervalos de tempo (horas).
Figura 1 – Gráfico de frequência das falhas
Fonte: Os autores
Na Figura 2, é possível observar a representação gráfica que descreve a taxa de falha ou risco para o conjunto de dados.
Figura 2 – Taxa de falha

Fonte: Os autores
A Figura 3 mostra que os dados apresentam uma relação relativamente constante até o tempo de 170 horas, seguida por uma elevação bem caracterizada da taxa de falha.
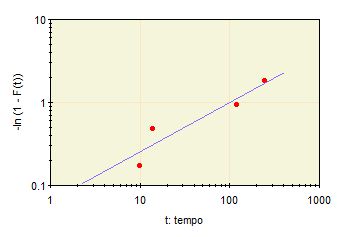
A análise gráfica é refinada pelo papel de probabilidade, que transforma os dados em uma distribuição de probabilidade que se aproxima de uma reta. Quanto mais próximos os dados estiverem da reta, melhor eles se ajustam à distribuição hipotetizada. A Figura 3 mostra o papel de probabilidade para a distribuição de Weibull, uma das distribuições mais importantes na modelagem de confiabilidade devido à sua flexibilidade e capacidade de representação de amostras de tempos até falha com comportamentos distintos.
Figura 3 – Gráfico de linearização da distribuição Weibull.

Fonte: Os autores
Os níveis de significância para os testes de aderência de Qui-Quadrado (χ2 ) e de Kolmogorov-Smirnov (K-S) estão apresentados na Tabela 2:
Tabela 2 – Valor dos testes de aderência.
MODELO Χ 2 K-S RESULTADO Exponencial 0,6583 0,0626 Não pode ser rejeitada Lognormal 0,3632 0,2017 Não pode ser rejeitada Normal 0,1447 0,0039 Rejeitada Weibull 0,3427 0,3055 Não pode ser rejeitada
Fonte: Os autores
A distribuição Normal não foi considerada adequada para modelar a amostra de dados. Para que fosse considerada, os níveis de significância dos testes para ambas as distribuições teriam que ser maiores que 0,05.
O presente estudo utilizará a distribuição Weibull para modelar o tempo de falha, mesmo que duas outras distribuições não tenham sido rejeitadas, pois, como citado anteriormente, a distribuição Weibull é uma das mais importantes na modelagem de confiabilidade, devido à sua flexibilidade e capacidade de representar amostras de tempos até falha com comportamentos distintos.
Após a escolha do modelo, foi possível estimar seus parâmetros, bem como outros resultados dos ajustes realizados pelo ProConf. A Tabela 3 apresenta os valores limites de tempo em que 10% e 50% das falhas ocorreram (t10 e t50). Também são apresentados os parâmetros da distribuição Weibull, estimados como γ e θ.
Tabela 3 – Resultados dos ajustes – Weibull
PARÂMETRO RESULTADO t10 (horas) 0,8704 t50 (horas) 34,3233 MTTF (horas) 134,1233 γ 0,8385 θ 88,0718
Fonte: Os autores
De acordo com a Tabela 3, o tempo médio até a falha (MTTF) da dobradeira é de 134,1233 horas. Metade das falhas ocorreram antes de 34,3233 horas. Além disso, os parâmetros de forma γ e escala θ da Weibull são, respectivamente, 0,8385 e 88,0718.
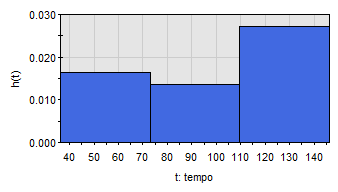
Os resultados indicam que a função de risco (falha) é decrescente, pois o parâmetro de forma da distribuição Weibull, γ, é menor que 1, representado graficamente pela figura 4.
Figura 4 – Gráfico da função de risco h(t)
Fonte: Os autores
A função de risco do equipamento é decrescente, mas com tendência a estabilização. A determinação precisa da fase em que o equipamento se encontra requer mais informações sobre a máquina e suas falhas. No entanto, de acordo com a teoria, o fato de o parâmetro de forma da distribuição Weibull, γ, ser menor que 1 indica que o equipamento está na fase de mortalidade infantil, em que a manutenção corretiva é a mais indicada. Contudo, o valor de γ estar próximo de 1 indica que o equipamento está entrando na fase de vida útil, em que a manutenção preditiva é a mais indicada.
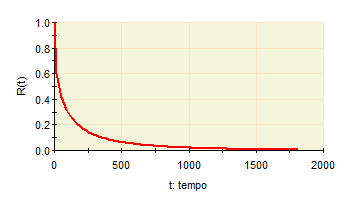
A confiabilidade do equipamento é representada na Figura 5.
Figura 5 – Gráfico da função Confiabilidade R(t)
Fonte: Os autores
A confiabilidade diminui ao longo do tempo, o que significa que a probabilidade de falha aumenta.
4.5 CORTE A LASER
A Figura 6 exibe a relação entre o número de falhas e o tempo (horas).
Figura 6 – Gráfico de frequência das falhas
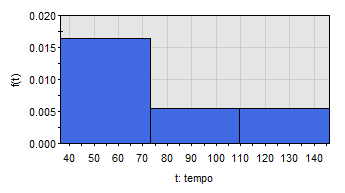
Fonte: Os autores
A Figura 7 representa graficamente a taxa de falha ou risco para os dados da máquina de corte a laser, que apresentam uma relação relativamente decrescente até o tempo de 110 horas, com posterior elevação bem caracterizada da taxa de falha.
Figura 7 – Taxa de falha

Fonte: Os autores
O papel de probabilidade para a distribuição de Weibull é mostrado na figura 8.
Figura 8 – Gráfico de linearização da distribuição Weibull.
Fonte: Os autores
Os níveis de significância para os testes de aderência de Qui-Quadrado (χ2) e de Kolmogorov-Smirnov (K-S) estão apresentados na Tabela 4:
Tabela 4 – Valor dos testes de aderência.
MODELO χ 2 K-S RESULTADO Exponencial 0,7194 0,0046 Rejeitada Lognormal 0,1408 0,0941 Não pode ser rejeitada Normal 0,1406 0,0524 Não pode ser rejeitada Weibull 0,2566 0,1773 Não pode ser rejeitada
Fonte: Os autores
A distribuição Exponencial não foi considerada adequada para modelar a amostra de dados, pois o nível de significância do teste Kolmogorov-Smirnov (K-S) foi menor que 0,05.
O presente estudo utilizará a distribuição Weibull para modelar o tempo de falha, a Tabela 5 apresenta os valores limites de tempo em que 10% e 50% das falhas ocorreram (t10 e t50) e os parâmetros estimados como γ e θ.
Tabela 5 – Resultados dos ajustes – Weibull
PARÂMETRO RESULTADO t10 (horas) 18,7131 t50 (horas) 63,8231 MTTF (horas) 72,9517 γ 2,2015 θ 86,8141
Fonte: Os autores
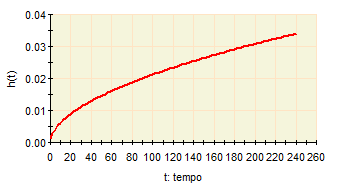
De acordo com a Tabela 5, o tempo médio até a falha (MTTF) da Corte a Laser é de 72,9517 horas. Metade das falhas ocorreram antes de 63,8231 horas. Além disso, os parâmetros de forma γ e escala θ da Weibull são, respectivamente, 2,2015 e 86,8141.Os resultados indicam que a função de risco (falha) é crescente, pois o parâmetro de forma da distribuição Weibull, γ, é maior que 1, representado graficamente pela Figura 9.
Figura 9 – Gráfico da função de risco h(t)

Fonte: Os autores
O fato de o parâmetro de forma da distribuição Weibull, γ, ser maior que 1 indica que o equipamento está na fase de mortalidade senil, em que a manutenção preventiva é a mais indicada, pois nesta fase é necessário realizar a troca dos componentes frágeis, que estão prestes a falhar.
A Figura 10 representa a função de confiabilidade. Observa-se que a confiabilidade diminui com o tempo, formando uma curva decrescente.
Figura 10 – Gráfico da função Confiabilidade R(t)
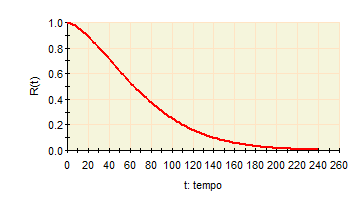
Fonte: Os autores
6 CONCLUSÃO
Por meio de estudos quantitativos de confiabilidade, podemos definir, de maneira científica, parâmetros que fornecem um suporte preciso para decisões sobre práticas de manutenção, operação e investimentos.
Ao utilizar métodos gráficos e analíticos, identificou-se que a distribuição Weibull é a mais adequada para modelar os dados estudados. Isso permitiu a obtenção de medidas de confiabilidade, como o tempo médio até a falha e os limites de tempo nos quais ocorreram 10% e 50% das falhas. Além disso, foi possível estimar os parâmetros dessa distribuição ajustada. Simultaneamente, foi possível ver a necessidade de desenvolver um plano de manutenção específico para cada estágio da curva de vida útil do equipamento, a fim de prevenir a ocorrência de falhas.
É importante ressaltar que para obter resultados mais precisos, seria necessário o fornecimento de informações adicionais acerca das falhas específicas e das características do equipamento. A disponibilidade de dados mais detalhados contribuiria para a confiabilidade dos resultados obtidos, otimizando assim as recomendações relacionadas à gestão da manutenção do referido equipamento.
Em resumo, a análise do estudo de caso com discussão revelou-se eficaz, especialmente considerando que a confiabilidade é uma técnica em desenvolvimento e ainda pouco explorada na indústria brasileira. Assim, a empresa poderá se preparar melhor para lidar com as falhas, criando um plano de gestão de manutenção e expandindo para os outros equipamentos disponíveis pela fábrica, uma vez que tomar decisões com base em tentativa e erro pode acarretar problemas significativos para a companhia.
6 REFERÊNCIAS
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 5462. Confiabilidade e manten-abilidade. Rio de Janeiro: ABNT, 1994.
FOGLIATTO, Flávio. Confiabilidade e Manutenção industrial. Grupo GEN, 2009.
GREGÓRIO, Gabriela Fonseca Parreira; SILVEIRA, Aline Morais da. Manutenção industrial. Porto Alegre: SAGAH, 2018.
FREITAS, M.A., Colossimo E.A.; Confiabilidade: análise de tempo de falha e testes de vida acelerados. Ed. Fundação Christiano Ottoni, Belo Horizonte, 1997.
LEWIS, E.E., Introduction to Reliability Engineering, John Wiley & Sons, New York, 1987.
ANDRADE, Paulo César de Resende; MACIEL, Gabriel Acyprest. Modelagem dos dados de falha de uma bomba de refrigeração de alto-forno. Revista THEMA, v. 19, n. 3, p. 721-730, ago. 2021.
BRANDÃO, Mariane Oliviera; ANDRADE, Paulo César de Resende. Modelagem dos dados de falhas de um pasteurizador de garrafas de cerveja. Revista de Engenharia e Tecnologia, ISSN 2176-7270, v. 10, n. 2, p. 181, 2018.
SELLITTO, Miguel Afonso. Análise estratégica da manutenção de uma linha de fabricação metal-mecânica baseada em cálculos de confiabilidade de equipamentos. São Leopoldo-RS. Ano 2, v. 3, p. 97-108, 2007.
KARDEC, Alan; NASCIF, Julio. Manutenção: Função Estratégica. 5ª edição. Qualitymark, 2012.
1Ra: 819118657 Engenharia Mecânica
2 Ra: 819166219 Engenharia Mecânica
3 Ra: 819163330 Engenharia Mecânica
4 Ra: 822162604 Engenharia Mecânica
5 Ra: 823153171 Engenharia Mecânica
6 Ra: 819163316 Engenharia Mecânica
7 Ra: 823159908 Engenharia Mecânica
8 Orientador: Ms.

