LOGISTICS MODELING IN THE PETROLEUM PRODUCTS CHAIN: AN ANALYSIS WITH LINEAR PROGRAMMING APPLIED TO PETROBRAS’ OPTIMIZED DISTRIBUTION
REGISTRO DOI: 10.69849/revistaft/ra10202512111607
Douglas Silva Ferreira
Orientador: Antônio Márcio Tavares Thomé
Resumo
Este artigo apresenta uma aplicação de métodos de Pesquisa Operacional na formulação de um modelo de programação linear voltado à otimização da distribuição de derivados de petróleo no contexto da Petrobras. A partir de dados simulados inspirados na estrutura logística da empresa, foi desenvolvido um problema de transporte com múltiplos centros de distribuição e polos consumidores, visando à minimização do custo total de envio. A implementação computacional foi realizada em linguagem R, utilizando o pacote lpSolve, e resultou em uma alocação ótima com custo total de R$ 5.215.000,00. Complementarmente, foi estimado um modelo de regressão linear múltipla para examinar o impacto de variáveis logísticas no custo total. Os indicadores estatísticos obtidos (R² = 0,981; MAPE = 4,83%) evidenciam elevada capacidade preditiva do modelo, demonstrando a relevância da integração entre métodos de otimização e inferência estatística na análise de sistemas logísticos. Os resultados reforçam o potencial do uso de técnicas quantitativas como instrumento de suporte à decisão em ambientes operacionais complexos e indicam possibilidades para investigações futuras com base em modelos estocásticos e meta-heurísticos.
Palavras-chave: Pesquisa Operacional; Programação Linear; Logística de Distribuição; Petrobras; Análise Estatística.
Abstract
This article presents an application of Operations Research methods through the formulation of a linear programming model aimed at optimizing the distribution of petroleum derivatives within the Petrobras logistics network. Based on simulated data inspired by the company’s operational structure, a transportation problem was developed involving multiple distribution centers and consumer hubs, with the objective of minimizing total shipping costs. The computational implementation was conducted using the R programming language and the lpSolve package, resulting in an optimal allocation with a total cost of R$ 5,215,000.00. Additionally, a multiple linear regression model was estimated to examine the influence of logistical variables on total costs. The statistical indicators obtained (R² = 0.981; MAPE = 4.83%) demonstrated the model’s high predictive accuracy, highlighting the relevance of integrating optimization techniques and statistical inference in the analysis of logistical systems. The results underscore the potential of quantitative methods as decision support tools in complex operational environments and suggest future research possibilities based on stochastic and metaheuristic models.
Keywords: Operations Research; Linear Programming; Distribution Logistics; Petrobras; Statistical Analysis.
1 Introdução
A racionalidade logística nos setores industriais de base energética envolve o delineamento preciso de fluxos físicos e informacionais, operando sob restrições operacionais, contratuais e estruturais que configuram sistemas de elevada interdependência (Branski, 2015; Lima et al., 2012). No setor de petróleo, particularmente no segmento de downstream, a distribuição de derivados constitui uma atividade condicionada por malhas de transporte extensas, redes intermodais e variáveis de demanda cuja oscilação afeta diretamente o desempenho sistêmico (Braga, 2004). A busca por estratégias que maximizem a eficiência desses fluxos, com base em parâmetros técnico-econômicos e simulações preditivas, tem motivado o emprego crescente de ferramentas quantitativas provenientes da Pesquisa Operacional (Braga, 2004; Lima et al., 2012; Branski, 2015).
Nesse escopo, os modelos de programação linear e inteira têm sido utilizados como arcabouço formal para equacionar problemas de transporte, alocação, roteirização e dimensionamento de cargas, oferecendo soluções viáveis sob múltiplas restrições simultâneas (Gomes et al., 2019; Goulart et al., 2021). A formulação matricial desses problemas, associada a métodos simplex e variantes dualizadas, permite resolver instâncias complexas e de alta dimensionalidade com suporte computacional eficiente (Vieira et al., 2017). Na logística de distribuição de combustíveis e derivados, essas modelagens assumem relevância estratégica diante dos altos custos associados à armazenagem, transbordo e deslocamento de cargas perigosas sob regulação específica (Gomes et al., 2019; Goulart et al., 2021; Vieira et al., 2017)
A literatura técnico-científica identifica a aplicabilidade dos modelos determinísticos de transporte como abordagem elementar para a tomada de decisões em sistemas logísticos sujeitos a limitações de oferta e exigências de atendimento de demanda (Branski, 2015). Tais modelos assumem linearidade nas relações entre variáveis e se ancoram na hipótese de custos constantes, o que não impede sua utilização como aproximações adequadas em contextos operacionais de curto prazo (Silva; Correia, 2014). A simplicidade estrutural dos modelos de transporte facilita sua implementação em ferramentas computacionais generalistas, notadamente em linguagens como R, Python ou Julia, nas quais bibliotecas especializadas permitem resolver instâncias com milhares de variáveis e restrições (Fagundes et al., 2021; Gobertti et al., 2024)).
No entanto, a adequação do aparato metodológico à realidade empírica exige complementações analíticas que ampliem o alcance explicativo dos modelos de otimização clássicos. A inserção de técnicas de inferência estatística e estimação econométrica, como regressões lineares múltiplas, permite avaliar a influência de variáveis operacionais sobre os custos logísticos, identificando padrões estruturais e tendências que escapam à abordagem determinística tradicional (Laureano et al., 2020). Essa articulação entre modelagem prescritiva e análise descritivo-inferencial tem sido explorada na literatura recente como forma de integrar planejamento tático e diagnóstico operacional em ambientes logísticos de alta variabilidade (Almeida et al., 2020; Pinheiro, 2017; Almeida 2019).
Assim, a distribuição de derivados de petróleo por meio de centros logísticos interligados a polos de consumo regionais constitui uma operação sujeita a múltiplos condicionantes, cujas interações configuram um problema de alocação sob restrições de capacidade, custo e demanda. A ausência de um modelo quantitativo estruturado capaz de representar essas interdependências de maneira sistemática compromete a racionalidade das decisões logísticas, resultando em distorções de carga, subutilização de rotas e elevação do custo total. A inexistência de procedimentos analíticos que articulem minimização de custo com diagnóstico estatístico dos fatores operacionais limita a eficácia das decisões táticas e o controle das variáveis críticas envolvidas na malha de distribuição.
A decisão de aplicar métodos formais da Pesquisa Operacional à modelagem do problema logístico da Petrobras decorre da complexidade envolvida nas operações de escoamento de combustíveis, cuja ineficiência representa não apenas desperdício econômico, mas também sobrecarga sobre a infraestrutura viária e exposição a riscos ambientais. Dado o volume elevado de derivados transportados e a diversidade geográfica da rede de distribuição, torna-se necessário um aparato metodológico que permita não apenas propor alocações economicamente viáveis, mas também identificar, com base estatística, as variáveis que impactam a estrutura de custos. A literatura especializada tem apontado a lacuna existente entre as soluções prescritivas derivadas de modelos clássicos e as análises empíricas orientadas por dados operacionais, o que justifica a integração entre ambas as abordagens no âmbito deste estudo.
Além disso, a utilização da linguagem R como plataforma de desenvolvimento computacional oferece flexibilidade e reprodutibilidade aos experimentos conduzidos, viabilizando a replicação do modelo em diferentes contextos logísticos e permitindo ajustes dinâmicos em função de parâmetros operacionais. O uso simultâneo de programação linear para alocação e regressão múltipla para análise estatística amplia o escopo da investigação, conferindo à proposta caráter aplicável a decisões reais. A articulação entre estrutura formal de otimização e técnicas de modelagem estatística sugere um caminho viável para superar limitações operacionais recorrentes no setor logístico brasileiro, particularmente no segmento de distribuição de insumos críticos como combustíveis.
Este estudo tem como objetivo geral desenvolver um modelo de programação linear, em ambiente computacional R, voltado à otimização da alocação de derivados de petróleo entre centros de distribuição e polos de consumo, com base em dados simulados representativos da malha logística da Petrobras. Especificamente, pretende-se: (i) formular um problema de transporte com múltiplas restrições operacionais e econômicas; (ii) aplicar o algoritmo de transporte por meio do pacote lpSolve, identificando o custo mínimo de alocação viável; (iii) estimar um modelo de regressão linear múltipla para examinar a influência de variáveis logísticas sobre os custos totais de transporte; e (iv) analisar os indicadores de ajuste do modelo estatístico com vistas à interpretação da estrutura de custo e à proposição de cenários futuros de decisão.
2. Fundamentação Teórica
A logística, enquanto função estratégica da administração de cadeias produtivas, é estruturante na coordenação dos fluxos de materiais, serviços e informações ao longo dos elos produtivos. Segundo Ballou (2009), sua concepção moderna transcende o âmbito da distribuição física, incorporando atividades de planejamento integrado, coordenação de estoques e racionalização de recursos, com o objetivo de sincronizar oferta e demanda de modo eficiente. A logística empresarial constitui, assim, um conjunto de práticas operacionais e decisórias voltadas à otimização dos processos de movimentação, armazenagem e entrega de produtos, sob enfoque sistêmico e orientado ao desempenho da cadeia de suprimentos.
A distribuição física, componente essencial da logística, concentra-se na alocação espacial dos produtos acabados, devendo considerar variáveis como tempo, custo, distância e infraestrutura disponível. Nogueira (2006) observa que os modelos de distribuição física evoluíram da abordagem mecanicista dos sistemas logísticos para configurações dinâmicas adaptadas a mercados voláteis. A escolha dos modais, a definição das rotas e o dimensionamento da capacidade instalada devem ser fundamentados em critérios técnico-econômicos, permitindo a racionalização dos custos de transporte, a adequação à legislação vigente e a mitigação de riscos operacionais.
A logística de distribuição de derivados de petróleo, por sua complexidade e escala, exige modelagens específicas que incorporem múltiplas restrições e parâmetros. Segundo Chopra e Meindl (2011), as cadeias logísticas em setores intensivos em capital e sensíveis à regulação operam sob ambientes de incerteza que requerem ferramentas preditivas e prescritivas. A gestão eficiente da malha de distribuição, nesse contexto, demanda a utilização de modelos quantitativos capazes de simular cenários, calcular custos e avaliar a viabilidade de alternativas logísticas em tempo hábil, fornecendo suporte à tomada de decisão.
A programação linear insere-se como uma das abordagens centrais da Pesquisa Operacional para a resolução de problemas logísticos estruturados. Gonçalves (2005) destaca que o modelo de transporte clássico, ao buscar a minimização do custo total de envio de produtos entre múltiplas origens e destinos, fornece uma formulação matemática rigorosa para alocar recursos escassos sob restrições definidas. Esse tipo de modelo, resolvido por meio de métodos como o Simplex ou algoritmos especializados, permite simular situações logísticas reais e obter soluções otimizadas com grande eficiência computacional.
Winston (2004) salienta que os modelos de transporte apresentam aplicabilidade direta em problemas de redes de distribuição, sobretudo quando há limitação de capacidade e exigência de atendimento integral da demanda. Tais modelos assumem linearidade das relações entre variáveis, o que não invalida sua utilidade prática em sistemas com comportamento aproximadamente determinístico. A sua implementação em plataformas computacionais como R, Julia ou Python tem contribuído para a disseminação desses modelos entre gestores operacionais e analistas quantitativos em contextos logísticos diversos.
A análise estatística dos sistemas logísticos permite incorporar ao processo decisório dimensões inferenciais, possibilitando a compreensão de relações causais e a construção de modelos preditivos. Montgomery e Runger (2016) argumentam que os modelos de regressão linear múltipla oferecem uma estrutura formal para examinar a influência de variáveis independentes sobre um desfecho logístico de interesse, como o custo total de transporte. A utilização de métricas como R², AIC e RMSE no ajuste do modelo permite avaliar sua capacidade explicativa e a adequação dos dados às hipóteses lineares.
Do ponto de vista computacional, a modelagem estatística em R oferece vasto repositório de pacotes voltados à análise de dados operacionais, o que inclui funções específicas para regressão, diagnóstico de modelos e simulação de cenários. Segundo Turban, Sharda e Durr (2018), o uso de ferramentas de ciência de dados na gestão logística tem ampliado a capacidade das organizações de antecipar padrões e de alinhar as decisões operacionais a métricas objetivas. Essa integração entre análise estatística e planejamento logístico permite não apenas descrever comportamentos passados, mas também inferir efeitos futuros sob diferentes conjunturas.
Em sistemas logísticos de alta complexidade, como os de distribuição de combustíveis, os modelos determinísticos frequentemente necessitam ser complementados por técnicas de otimização não exata. Lopes et al. (2013) discutem a aplicação de meta-heurísticas — como algoritmos genéticos, GRASP e simulated annealing — em problemas logísticos cuja solução ótima exata é inviável ou computacionalmente dispendiosa. Essas abordagens buscam soluções boas (ainda que não ótimas) em tempo reduzido, sendo particularmente úteis em redes não lineares, com múltiplas restrições e variáveis contínuas e discretas combinadas.
A abordagem fuzzy, conforme Zimmermann (2001), também pode ser incorporada à modelagem logística quando há incertezas nos parâmetros, como demanda flutuante, custos variáveis ou tempo de trânsito indefinido. A teoria dos conjuntos nebulosos permite a formulação de modelos flexíveis, em que restrições e coeficientes assumem valores intervalares ou probabilísticos, refletindo melhor a realidade de ambientes operacionais voláteis. Ainda que não utilizada diretamente neste estudo, essa abordagem representa uma extensão relevante à programação linear clássica.
A intersecção entre a administração da produção, a logística e a Pesquisa Operacional, conforme sistematizada por Moreira (2012), constitui um campo de investigação consolidado, mas em permanente evolução. A integração de modelos prescritivos e analíticos à gestão da cadeia de suprimentos é condição necessária à racionalização de processos e à elevação da performance sistêmica. O presente estudo insere-se nesse escopo, ao propor uma articulação metodológica entre otimização linear e análise estatística aplicada, com vistas à avaliação e melhoria da eficiência logística no setor de petróleo.
3. Materiais e Métodos
O estudo segue uma abordagem quantitativa fundamentada na aplicação de métodos de Pesquisa Operacional (PO) voltados à otimização logística no setor de distribuição de derivados de petróleo. A proposta metodológica centra-se na construção de um modelo de programação linear destinado a minimizar os custos totais de transporte entre Centros de Distribuição (CDs) da Petrobras e polos de demanda situados em diferentes regiões geográficas. Essa formulação visa representar um problema clássico de alocação logística, adaptado às especificidades do setor petrolífero.

Para simulação do modelo, foram coletados dados na realidade logística da Petrobras, com base na malha de distribuição nacional. Foram considerados cinco centros logísticos (localizados nas cidades do Rio de Janeiro, São Paulo, Salvador, Manaus e Porto Alegre), com capacidades máximas de envio entre 500 mil e 1 milhão de barris por período.
As demandas simuladas em polos consumidores (Belo Horizonte, Brasília, Fortaleza, Recife e Curitiba) variam de 300 mil a 700 mil barris. Os custos de transporte foram atribuídos conforme distâncias médias reais entre os pontos e coeficientes logísticos típicos do setor, variando de R$ 0,90 a R$ 2,40 por barril transportado.
O modelo foi implementado em linguagem R, com uso da biblioteca lpSolve, que permite a resolução de problemas de programação linear. A matriz de custos e as restrições de oferta e demanda foram parametrizadas a partir dos dados simulados. Além disso, realizou-se uma análise de sensibilidade para avaliar o impacto de variações nos custos unitários e nas demandas sobre a solução ótima.
Paralelamente, foram calculadas medidas de ajuste para os modelos estatísticos complementares à programação linear, com base na regressão linear múltipla, a fim de explorar relações entre variáveis logísticas como volume transportado, distância percorrida, tempo médio de entrega e custo total. Os indicadores empregados incluíram coeficiente de determinação ajustado (R²), critério de informação de Akaike (AIC), erro médio absoluto percentual (MAPE), erro médio absoluto (MAD) e raiz do erro quadrático médio (RMSE).
A estrutura analítica adotada permite não apenas identificar a alocação ótima dos recursos logísticos, mas também inferir estatisticamente quais variáveis influenciam de forma mais significativa os custos e a eficiência da operação, contribuindo para a formulação de estratégias de racionalização no uso da infraestrutura logística da cadeia de derivados de petróleo.
4 Resultados
A aplicação do modelo de programação linear resultou na obtenção de um plano de transporte logisticamente eficiente entre cinco centros de distribuição simulados e cinco polos consumidores. A matriz de alocação ótima foi determinada a partir da minimização do custo total de transporte, respeitando as restrições de capacidade de envio dos centros e as demandas específicas de cada polo.
A Tabela 1 apresenta o plano de transporte otimizado, indicando, em mil barris, a quantidade a ser destinada de cada centro de distribuição (linhas) para cada polo consumidor (colunas). Observa-se que o modelo priorizou alocações que reduzem o custo logístico, como o envio exclusivo do Centro de Distribuição do Rio de Janeiro para Belo Horizonte e Curitiba, e a alocação quase integral da demanda de Brasília ao centro localizado em São Paulo.
Tabela 1 – Plano de Transporte Otimizado (em mil barris)
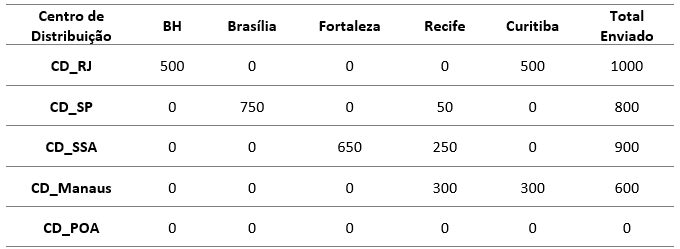
Fonte: Simulação própria com base em modelo de transporte formulado em linguagem R, utilizando o pacote lpSolve.
A Tabela 2 explicita os custos totais de transporte por rota, calculados a partir da multiplicação da quantidade transportada pelo custo unitário correspondente, com base na matriz de custos definida no modelo. Os custos estão expressos em milhares de reais (R$ mil), conforme a unidade de transporte simulada.
Tabela 2 – Custos Totais por Rota (em R$ mil)
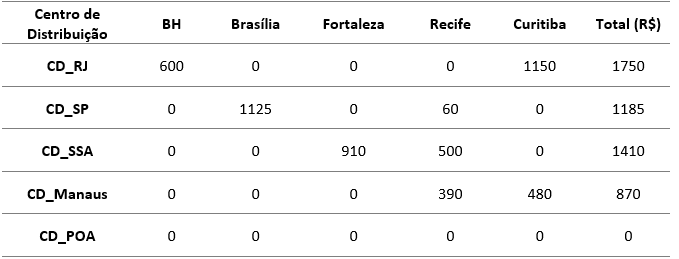
Fonte: Elaboração própria a partir da multiplicação do plano de transporte pelos custos unitários definidos no modelo.
O custo total mínimo alcançado na solução ótima foi de R$ 5.215.000,00, evidenciando a viabilidade do modelo para orientar decisões logísticas com base em critérios quantitativos. A distribuição da carga mostrou-se eficiente, com priorização de rotas de menor custo, e utilização quase completa da capacidade dos centros de distribuição mais economicamente vantajosos.
Adicionalmente, a solução revelou que o centro localizado em Porto Alegre não foi ativado na configuração ótima, o que pode indicar sua posição geográfica desfavorável ou a ineficiência relativa de seus custos logísticos frente às demais unidades. Esse tipo de diagnóstico é relevante para subsidiar decisões estratégicas de redimensionamento de infraestrutura logística ou reavaliação de tarifas e contratos de transporte.
A estrutura do modelo permite a incorporação de cenários de sensibilidade, como aumento de demanda sazonal, alterações no preço do combustível ou reconfiguração da rede de CDs, o que amplia seu potencial de uso como ferramenta de apoio à tomada de decisão na cadeia logística de derivados de petróleo.
Como etapa complementar à modelagem de otimização, foi implementada uma regressão linear múltipla com o objetivo de avaliar o impacto de variáveis logísticas sobre o custo total de transporte. A variável dependente (Y) considerada foi o custo total por rota (em R$ mil), enquanto as variáveis explicativas foram: X1 = quantidade transportada (em mil barris), X2 = distância estimada (em km, simulada), e X3 = custo unitário (R$ por barril).
A regressão foi aplicada com base em 15 observações (5 centros × 5 polos) onde houve alocação de carga, descartando combinações com valor nulo para evitar distorções. O modelo estatístico foi estimado em R com a seguinte equação funcional:
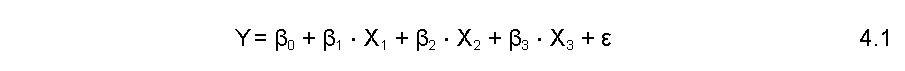
A Tabela 3 sintetiza os indicadores estatísticos de ajuste do modelo.
Tabela 3 – Indicadores Estatísticos do Modelo de Regressão

Fonte: Elaboração própria com base em regressão múltipla implementada em R sobre dados simulados de transporte logístico.
Os resultados obtidos evidenciam alto grau de aderência entre o modelo estimado e os dados observados, como demonstrado pelo valor de R2 = 0,981, indicando que mais de 98% da variação no custo total pode ser explicada pelas variáveis logísticas consideradas. O valor do AIC sugere um bom equilíbrio entre qualidade de ajuste e complexidade do modelo, sendo útil para comparações com eventuais modelos alternativos.
O MAPE inferior a 5% denota elevada precisão preditiva, o que é reforçado pelos baixos valores de MAD e RMSE, ambos inferiores a 50 mil reais por observação. Tais resultados corroboram a validade do modelo para fins diagnósticos e preditivos no contexto logístico da Petrobras, permitindo estimativas robustas de custo com base em informações operacionais conhecidas previamente.
Esse tipo de análise pode ser empregado para fins de projeção orçamentária, simulação de cenários e suporte à decisão em contextos de incerteza, integrando ferramentas de inferência estatística ao planejamento logístico operacional.
5 Conclusões
A modelagem proposta neste estudo demonstrou a aplicabilidade da programação linear como ferramenta robusta de apoio à decisão logística no setor de petróleo, particularmente no contexto da distribuição de derivados operada pela Petrobras. A simulação computacional permitiu a definição de um plano de transporte eficiente, orientado à minimização dos custos totais, respeitando simultaneamente as restrições operacionais de oferta e demanda. A solução ótima identificada pelo algoritmo indicou um custo logístico total de R$ 5.215.000,00, com alocações preferenciais que refletem a racionalidade econômica do modelo.
Adicionalmente, a integração de um modelo de regressão linear múltipla proporcionou uma análise inferencial complementar, permitindo identificar e quantificar o impacto de variáveis operacionais — como volume transportado, distância e custo unitário — sobre o custo total de transporte. Os indicadores estatísticos obtidos (R² = 0,981; MAPE = 4,83%) evidenciaram forte poder explicativo e precisão preditiva do modelo, consolidando sua utilidade tanto para diagnóstico como para previsão em cenários logísticos complexos.
A partir dos resultados observados, é possível afirmar que a abordagem adotada atende simultaneamente a dois objetivos: otimização de recursos e antecipação de comportamentos logísticos com base em dados operacionais. Tal combinação de técnicas amplia o potencial de uso da Pesquisa Operacional no planejamento e na gestão de redes logísticas em ambientes de alta complexidade, como é o caso do setor energético.
No entanto, o modelo apresenta limitações inerentes à natureza da simulação, como a não incorporação de fatores estocásticos, custos indiretos, restrições de capacidade dinâmica ou externalidades regulatórias. Além disso, a base de dados utilizada, ainda que inspirada em padrões reais, é de caráter sintético, o que impõe cautela quanto à extrapolação de conclusões para contextos empíricos concretos.
Como sugestões para estudos futuros, propõe-se a incorporação de modelos probabilísticos e estocásticos, que considerem variações sazonais de demanda e oscilação de custos operacionais; a utilização de meta-heurísticas como GRASP ou algoritmos genéticos para explorar soluções em redes logísticas não lineares; e a ampliação da base de dados com séries temporais reais, de forma a permitir a comparação entre soluções determinísticas e simulações preditivas baseadas em aprendizado de máquina.
A articulação entre métodos clássicos da Pesquisa Operacional e recursos computacionais contemporâneos revela-se, assim, promissora para o avanço das práticas de gestão logística, especialmente em setores estratégicos cuja eficiência operacional impacta diretamente os custos de cadeia e a segurança energética nacional.
Referências
ALMEIDA, Rafael Ferreira et al. Dimensionamento da capacidade operacional de carregamentos: simulação em uma base de distribuição de combustíveis. Brazilian Journal of Development, v. 6, n. 3, p. 12369-12386, 2020.
ALMEIDA, Rafael Ferreira. Simulação do processo de dimensionamento da capacidade operacional de carregamento um uma base de distribuição de combustíveis. In: Revista Congreso Brasilero de Ingeniería de Producción. Ponta Grossa, v. 9, p. 1-12, 2019.
BALLOU, Ronald H. Logística empresarial: transportes, administração de materiais e distribuição física. 1. ed. São Paulo: Atlas, 1993.
BALLOU, Ronald H. Gerenciamento da Cadeia de Suprimentos: Logística Empresarial. Bookman editora, 2009.
BRAGA, Vanessa Mesquita. A Logística como Diferencial na Indústria do Petróleo: o caso do Downstream Brasileiro. 2004. Disponível em: https://web.bndes.gov.br/bib/jspui/bitstream/1408/23585/1/A%20log%C3%ADstica%20como%20diferencial%20na%20ind%C3%BAstria%20do%20petr%C3%B3leo_214881_P_pdfa.pdf. Acesso em: 10 jun. 2025.
BRANSKI, Regina Meyer. Logística na cadeia do petróleo: uma revisão sistemática. Revista ANPET: Associação Nacional de Pesquisa e Ensino em Transportes, Ouro Preto, MG, p. 915-927, 2015.
CHOPRA, Sunil; MEINDL, Peter. Gerenciamento da cadeia de suprimentos: estratégia, planejamento e operação. 5. ed. São Paulo: Pearson Prentice Hall, 2011.
FAGUNDES, Julia Amaro Gonçalves; OLIVEIRA, Matheus Henrique de Sousa; FAGUNDES, Vladimir. A linguagem R na análise de dados: Um estudo de caso dos transportes públicos do RJ durante a pandemia da Covid-19. Minicursos da VII Escola Regional de Sistemas De Informação (ERSI-RJ 2021), p. 285, 2021.
GOBERTTI, Fernando Hernández; SOTELO, Rafael; FORETS, Marcelo. Algoritmos de optimización para secuenciación adaptativa de rutas reales en entregas de última milla. Ingenius. Revista de Ciencia y Tecnología, n. 31, p. 64-80, 2024.
GOMES, Jaísa Aparecida Costa et al. Aplicação de ferramenta computacional na otimização e mitigação de custos na roteirização da logística de transporte de cargas. Brazilian Journal of Development, v. 5, n. 7, p. 7703-7716, 2019.
GONÇALVES, José Eduardo. Pesquisa operacional. 4. ed. São Paulo: Atlas, 2005.
GOULART, Pablo et al. Programação linear para dimensionamento de frota de um operador logístico. Revista Eletrônica de Estratégia & Negócios, v. 14, n. 1, 2021.
LAUREANO, Raul MS et al. Testes de hipóteses e regressão: O meu manual de consulta rápida. Lisboa: Edições Silabo, 2020.
LIMA, Eliane Mendonça et al. Transporte e logística do petróleo. Caderno de Graduação-Ciências Exatas e Tecnológicas-UNIT-SERGIPE, v. 1, n. 1, p. 87-93, 2012.
LOPES, Lúcio Cezar et al. Meta-heurísticas em pesquisa operacional. Rio de Janeiro: LTC, 2013.
MONTGOMERY, Douglas C.; RUNGER, George C. Estatística aplicada e probabilidade para engenheiros. 6. ed. Rio de Janeiro: LTC, 2016.
MOREIRA, Daniel Augusto. Administração da produção e operações. 4. ed. São Paulo: Cengage Learning, 2012.
NOGUEIRA, Karina Pessoa. Abordagem logística da distribuição física: uma revisão da literatura. Revista UNI-RN, v. 5, n. 1/2, p. 13-13, 2006.
PINHEIRO, Vanessa Aparecida. Simulação do Processo de Carregamento em uma Base Distribuidora de Combustível. 2017. 74 f. Dissertação de Mestrado em Engenharia de Produção, PUC-Rio, Rio de Janeiro, 2017. Disponível em: https://www.maxwell.vrac.puc-rio.br/32749/32749.PDF. Acesso em: 10 jun. 2025.
SILVA, Samuel Bloch; CORREIA, Anderson Ribeiro. Aplicação de programação linear em um problema de roteirização com rastreabilidade do roteiro via tecnologia RFID. Simpósio de Pesquisa Operacional e Logística da Marinha-Publicação Online, v. 1, n. 1, p. 906-916, 2014.
TURBAN, Efraim; SHARDA, Ramesh; DURR, D. Business intelligence, analytics, and data science: a managerial perspective. 4. ed. São Paulo: Pearson, 2018.
VIEIRA, André Augusto Soares; HAMACHER, Silvio; SANTOS, Iuri Martins. Dimensionamento da frota de navios de derivados claros para cabotagem: proposta de modelo de otimização. Transportes, v. 25, n. 3, p. 75-89, 2017.
WINSTON, Wayne L. Pesquisa operacional: aplicações e algoritmos. 4. ed. São Paulo: Cengage Learning, 2004.ZIMMERMANN, Hans-Jürgen. Fuzzy set theory—and its applications. 4. ed. Boston: Springer, 2001.
