REGISTRO DOI: 10.69849/revistaft/cl10202505151938
Cícero José da Silva
Willames de Albuquerque Soares
Sérgio Mário Lins Galdino
Jornandes Dias da Silva
Juan Carlos Oliveira de Medeiros
Resumo
Este artigo explora a integração das equações diferenciais (EDO) e (EDP) com as metodologias ativas no ensino do Cálculo e suas aplicações práticas as engenharias e física dos materiais, focados em projetos, exemplos práticos em uma viga sobrecarga distribuída ( EDO de segunda ordem),decaimento radioativo (EDO de primeira ordem) e para finalizar um problema de onda (EDP clássica) buscando propor desafios e questionamentos usando recursos computacionais, simular, valores diferentes para c ( velocidade da onda) e ver o que ocorre graficamente, considerar funções iniciais diferentes com forma triangular, quadrado, delimitar uma fronteira maior tudo `a luz das simulações.
Palavras-chave: Equações Diferenciais Ordinárias, Equações Diferenciais Parciais, Metodologias Ativas, Ensino de Cálculo, Simulações Computacionais, Engenharia, Física dos Materiais.
1. Introdução
O ensino de equações diferenciais ordinárias (EDOs) ´e um pilar fundamental no currículo de cálculo para as engenharias e ciências. A resolução dessas equações permite modelar uma grande variedade de fenômenos físicos e de engenharia, como a deflexão de vigas, o decaimento radioativo e a propagação de ondas. Embora a aprendizagem das EDOs seja essencial, ela pode ser desafiadora para os estudantes. Neste contexto, metodologias ativas de ensino oferecem uma abordagem inovadora que pode melhorar a compreensão, engajamento e aplicação prática dos conceitos.
As metodologias ativas, como a sala de aula invertida, aprendizagem baseada em problemas (PBL) e o uso de tecnologias de simulação e visualização, têm sido cada vez mais adotadas em diversas disciplinas. No caso das EDOs, essas abordagens podem ser usadas para tornar o aprendizado mais dinâmico, permitindo aos alunos explorar problemas reais de engenharia e física de maneira interativa. Este artigo visa integrar as EDOs com metodologias ativas, utilizando dois exemplos: o problema de deflexão de uma viga (engenharia) e o problema de decaimento radioativo (física). integrar as EDP com metodologias ativas, utilizando exemplo da equação de onda, poderia ser o mesmo modelo da modelagem matemática para transmissão de calor.
2. Deflexão de uma Viga Sob Carga Uniforme: EDO de Segunda Ordem
Consideremos uma viga de apoio simples, com comprimento L = 5m, sujeita a uma carga distribuída uniforme q(x) = 100N/m. O objetivo ´e calcular a deflexão máxima da viga, utilizando a equação diferencial que descreve o comportamento da viga sob carga.
A equação que descreve a deflexão de uma viga submetida a uma carga distribuída uniforme é dada por:
onde y(x) é a deflexão da viga, E é o módulo de elasticidade e I é o momento de inércia da viga. Para uma carga distribuída uniforme q(x) = 100N/m, a equação diferencial se torna:
Esta equação pode ser resolvida considerando as condições de contorno y(0) = 0 e y(L) = 0, que representam as condições de apoio simples na viga. A solução geral para a deflexão da viga é dada por:
Agora, substituindo os valores de L = 5m, E = 2 × 1011 N/m2, I = 1.2 × 10−6 m4, e q = 100N/m, podemos calcular a deflexão máxima ymáxima da viga. Esse processo pode ser visualizado e simulado com softwares como MATLAB, Wolfram Mathematica ou Python, proporcionando uma abordagem prática e visual para o entendimento das soluções de EDOs. [darkgreen] 1000*exp(-ln(2)*x);
3. Introdução
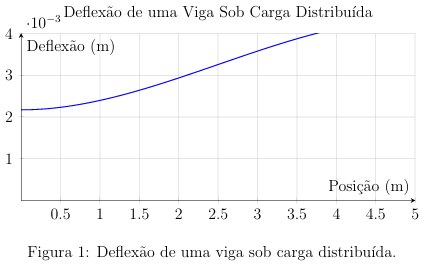
Neste documento, será apresentada a deflexão de uma viga de apoio simples submetida a uma carga distribuída constante ao longo de seu comprimento.
4. Problema
Uma viga de apoio simples com comprimento L = 5m, módulo de elasticidade E = 2×1011 N/m2, momento de inércia I = 1.2×10−6 m4 e carga distribuída q(x) = 100N/m será analisada. A deflexão máxima ocorre no centro da viga, e o gráfico da deflexão ao longo do comprimento da viga será calculado.
5. Equação da Deflexão
A deflexão y(x) ao longo da viga é dada pela seguinte equação:
onde x é a posição ao longo da viga.
6 Gráfico da Deflexão
O gráfico a seguir mostra a deflexão da viga ao longo de seu comprimento L = 5m.
7. Decaimento Radioativo: EDO de Primeira Ordem
O decaimento radioativo é descrito por uma equação diferencial de primeira ordem:
onde N(t) é a quantidade de material radioativo no tempo t e λ é a constante de decaimento. A solução dessa equação é dada por:
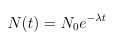
onde N0 é a quantidade inicial de material radioativo. Se tomarmos N0 = 1000g e λ = 0.1ano−1, a quantidade de material radioativo após 5 anos será:
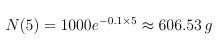
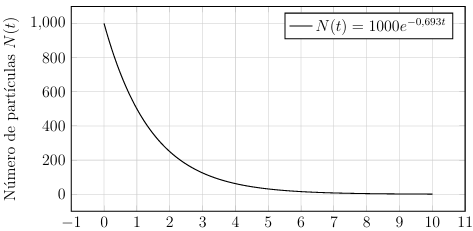
Simulação Gráfica do Decaimento Radioativo com Meia vida = 1
A equação diferencial que rege o decaimento radioativo é:
Para este caso, utilizamos:
- N0 = 1000
- λ = ln(2) ≈ 0,693, o que implica meia-vida igual a 1
- t ∈ [0,10]
Tempo t
Figura 2: Gráfico do decaimento radioativo com meia-vida igual a 1 unidade de tempo.
Simulação Gráfica do Decaimento Radioativo
A equação diferencial do decaimento radioativo é dada por:
Onde:
- N0 = 1000 (número inicial de partículas),
- λ = 0,2 (constante de decaimento),
- t em segundos.
Este problema pode ser abordado em sala de aula de forma interativa, com os alunos utilizando ferramentas de simulação para analisar como diferentes valores de λ afetam o tempo de vida do material radioativo.
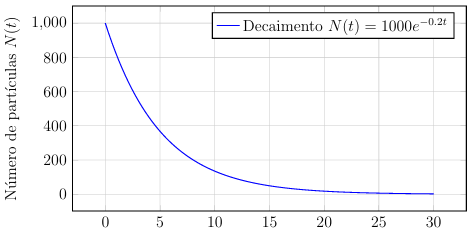
Tempo t (s)
Figura 3: Simulação do decaimento radioativo ao longo do tempo.
8. Integração das EDOs com Metodologias Ativas
A integração das EDOs com metodologias ativas permite que os alunos se envolvam de maneira prática com os conceitos, aplicando-os a problemas reais. Algumas abordagens incluem:
- Sala de Aula Invertida: Os alunos estudam os conceitos teóricos e matemáticos por meio de vídeos e materiais de leitura antes da aula. Durante a aula, eles resolvem problemas práticos como o de deflexão de vigas e decaimento radioativo com a orientação do professor.
- Aprendizagem Baseada em Problemas (PBL): Os alunos recebem um problema prático, como a modelagem de uma viga sob carga ou o estudo de decaimento radioativo, e devem utilizar EDOs para encontrar uma solução. O professor atua como facilitador, ajudando os alunos a desenvolver suas habilidades de resolução de problemas.
- Simulações Computacionais: Softwares como MATLAB, Python (com bibliotecas como NumPy e SciPy) e Wolfram Mathematica podem ser usados para simular a solução das EDOs. Isso permite que os alunos visualizem as soluções e experimentem com diferentes condições iniciais e parâmetros.
Estas abordagens, quando combinadas, não só ajudam os alunos a compreenderem a teoria das EDOs, mas também os capacitam a aplicar esses conhecimentos em situações reais, como o projeto de vigas em engenharia ou o estudo de materiais radioativos em física.
9. Conclusão
A integração das EDOs com metodologias ativas representa uma oportunidade de inovar o ensino de cálculo, tornando-o mais relevante e engajador para os alunos. Através de exemplos práticos de engenharia e física, como a deflexão de vigas e o decaimento radioativo, os alunos podem aplicar as EDOs em contextos reais, desenvolvendo habilidades essenciais para sua formação. As metodologias ativas, como a sala de aula invertida, a aprendizagem baseada em problemas e as simulações computacionais, são ferramentas poderosas para promover uma aprendizagem mais profunda e duradoura.
[12pt]article amsmath, amssymb pgfplots tikz geometry caption lipsum margin=2.5cm Metodologias Ativas e Resolução da Equação da Onda
1. Introdução
Neste estudo, combinamos a resolução matemática da Equação da Onda com a aplicação de metodologias ativas de ensino. O objetivo é promover um ambiente de aprendizagem mais participativo, onde os alunos possam compreender conceitos abstratos por meio da simulação computacional e de práticas investigativas.
2. Equação da Onda: Formulação e Resolução
A equação da onda unidimensional é dada por:
com condições de contorno:
u(0,t) = 0, u(L,t) = 0
e condição inicial:
2.1 Separação de Variáveis
Assumimos uma solução do tipo u(x,t) = X(x)T(t), e obtemos as equações:
X′′(x) + λX(x) = 0, T ′′(t) + c2λT(t) = 0
X(0) = X(L) = 0
2.2 Solução Geral
Com
temos:
3. Simulação Gráfica
4. Metodologias Ativas no Ensino de EDPs
4.1 Sala de Aula Invertida
Antes da aula presencial, os alunos assistem a vídeos com a resolução da equação da onda, exploram a teoria por meio de simuladores online, e leem um resumo interativo em PDF com perguntas guias. A aula ´e dedicada a` resolução de problemas práticos em grupo, com foco em interpretação física das soluções.
Soluções da equação da onda para diferentes tempos
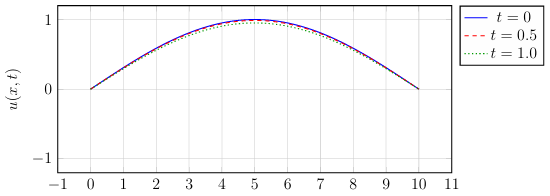
Figura 4: Solução da equação da onda para L = 10 e c = 1 com condição inicial f(x) =
4.2 Aprendizagem Baseada em Projetos (ABP)
Os estudantes desenvolvem projetos em duplas para simular o comportamento de uma corda em diferentes condições:
Alterando o valor de c (velocidade da onda)
Considerando outras funções iniciais, como uma forma triangular ou gaussiana
Estudando a propagação com fronteiras livres ou parcialmente fixas
4.3 Ensino por Investigação
Os alunos são desafiados a responder perguntas como:
Como o valor de c influencia a frequência da onda? E possível ter uma solução estacionária?´
O que acontece se f(x) for uma combinação de senos?
Eles testam hipóteses e verificam as respostas com simulações gráficas, promovendo aprendizado investigativo e reflexivo.
5. Considerações Finais
Ao combinar a modelagem matemática rigorosa com metodologias ativas, favorecemos a compreensão profunda de EDPs. O uso de gráficos, simulações e perguntas abertas aproxima a matemática da realidade e prepara os alunos para aplicações práticas e interdisciplinares.
1. Enunciado da Equação da Onda
Consideramos a equação da onda unidimensional:
com as seguintes condições de contorno e iniciais:
2. Método de Separação de Variáveis
Assumimos uma solução do tipo:
u(x,t) = X(x)T(t)
Substituindo na equação original:
X(x)T ′′(t) = c2X′′(x)T(t)
Dividindo ambos os lados por c2X(x)T(t), obtemos:
A igualdade a uma constante negativa −λ nos permite separar as variáveis.
3. Solução da Equação Espacial
A equação para X(x) se torna:
X′′(x) + λX(x) = 0, X(0) = X(L) = 0
As soluções são senoidais:
4. Solução da Equação Temporal
A equação para T(t) é:
T ′′(t) + c2λnT(t) = 0
Substituindo λn:
Solução geral:
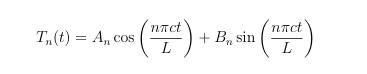
5. Solução Geral da EDP
Somando os modos:
6. Aplicação das Condições Iniciais
Dada a condição inicial u(x,0) = f(x), temos:
Ou seja, os coeficientes An são obtidos por projeção de Fourier:
Da condição ∂u∂t (x,0) = 0, obtemos:
7. Exemplo:
Nesse caso, apenas o termo n = 1 é diferente de zero:
A1 = 1, An = 0 para n ≥ 2
Logo:
8. Interpretação Física
Essa solução representa a vibração de uma corda presa nas extremidades, onde a forma inicial é um arco de seno, e a oscilação ocorre com frequência fundamental. A amplitude varia no tempo com um fator cossenoidal. pgfplots
9. Simulações Gráficas com Diferentes Valores de c
Para observar o efeito da velocidade da onda c na solução da EDP, apresentamos abaixo três gráficos para diferentes valores de c, fixando L = 10 e observando a solução para diferentes instantes de tempo.
9.1 Simulação com c = 0.5
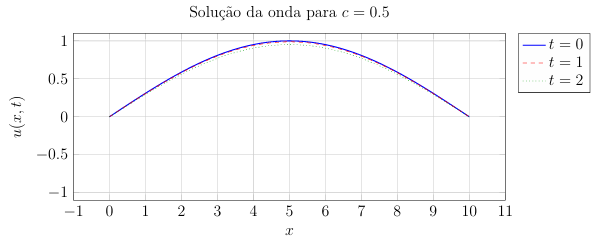
Figura 5: Evolução da solução com c = 0.5
9.2 Simulação com c = 1.0
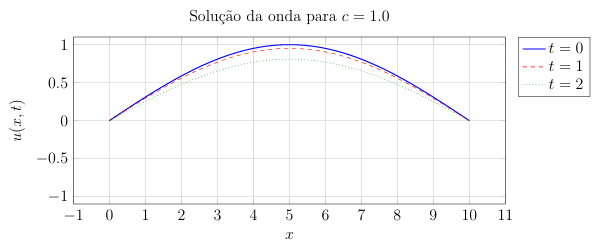
Figura 6: Evolução da solução com c = 1.0
9.3 Simulação com c = 2.0
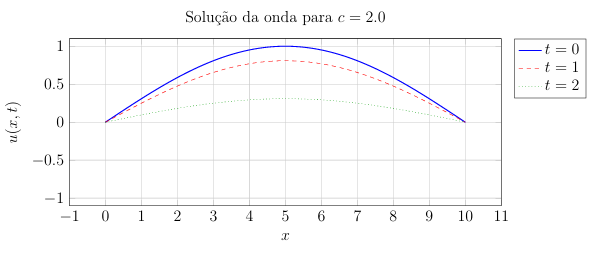
Figura 7: Evolução da solução com c = 2.0
Referências
- SciELO Brasil. Análise do potencial microbiano de uma biopilha na biorremediação de solos contaminados por hidrocarbonetos. Disponível em: https://www.scielo.br/j/esa/a/yycGJ6XbhTLXbtdsfK9Tvgx/.
- ALVES, R. I. S. et al. Avaliação de metais em águas superficiais em Ribeirão Preto, SP. Ambi-Agua, 2022.
- ANDRIANANTOANDRO, E. et al. Synthetic biology: engineering living systems. Nature Reviews Genetics, v. 7, p. 336–351, 2024.
- WAY, J. C. et al. Integrating biological redesign: where synthetic biology came from and where it needs to go. Cell, v. 157, n. 1, p. 151–161, 2024.
- GIBSON, D. G. et al. Creation of a bacterial cell controlled by a chemically synthesized genome. Science, v. 329, n. 5987, p. 52–56, 2020.
- CHANDRAN, D. et al. Design and implementation of a prototype biosynthetic pathway in Escherichia coli. Nature Protocols, v. 4, n. 12, p. 1685–1701, 2019.
- BRENNER, K.; YOU, L.; ARNDT, K. Toward a biosynthetic economy: integrating engineered microbes into the manufacturing process. Trends in Biotechnology, v. 26, n. 9, p. 483–489, 2008.
- NIELSEN, J.; KEASLING, J. D. Engineering cellular metabolism. Cell, v. 164, n. 6, p. 1185–1197, 2018.
- RAI, A.; PANDEY, N. Bioremediation of oil spills using synthetic biology approaches: recent advances and future prospects. Biotechnology Advances, v. 53, 2021.
- MODERN MEADOW. Biofabricated Materials. Disponível em: https://www. modernmeadow.com. Acesso em: abr. 2025.
- BIOSPHERE PLASTIC. Using synthetic biology to create biodegradable plastics. Journal of Industrial Biotechnology, v. 42, n. 3, p. 145–158, 2022.
- YADAV, V. G. et al. The future of industrial biomanufacturing with synthetic biology. Current Opinion in Biotechnology, v. 23, n. 6, p.
Universidade de Pernambuco (UPE)
cjs@poli.br
was@poli.br
galdino.sergio@gmail.com
jornandesdias@poli.br
juca@ufc.br
