GEOMETRIC STUDIES – CIRCLES
REGISTRO DOI: 10.69849/revistaft/ar10202508312158
José Silvio Filho
Resumo
O estudo analisa um novo método de calcular o perímetro do círculo através de polígonos regulares circunscritos nele. Trata-se de um estudo coerente e exato, onde foram analisados círculos de 3, 5 e 7 quadrados de diâmetro, medindo cada quadrado da malha aproximadamente 2,20 cm. Este método apresenta bons resultados, onde se obtém o valor do perímetro do círculo por meio de um valor absoluto igual a três vezes o diâmetro. Retificamos o estudo publicado pela Revista eletrônica Acervo Mais Revistas em 28/01/2020, intitulado Análise do Perímetro da Circunferência. Naquele estudo, o objetivo foi calcular o perímetro da circunferência. Já neste estudo, focaremos a parte interna da circunferência, o círculo, como base para o cálculo da capacidade, assim usaremos o termo perímetro do círculo para especificar ou diferenciar e também por se tratar da parte interna da circunferência, a parte disponível da esfera apta para ser preenchida, com por exemplo, por água. Neste estudo veremos que é hexágono circunscrito que tem o lado igual ao raio do círculo.
Palavras-Chaves: Hexágono. Circunscrito. Igual. Raio.
Abstract
This study analyzes a new method for calculating the perimeter of a circle using regular polygons circumscribed around it. It is a coherent and precise study where circles with diameters of 3, 5, and 7 squares were analyzed, with each grid square measuring approximately 2.20 cm. This method yields good results, where the value of the circle’s perimeter is obtained through a constant value equal to three times the diameter. We correct the study published in the electronic journal “Acervo Mais Revistas” on 01/28/2020, entitled ‘Analysis of the Circumference’s Perimeter.’ In that study, the objective was to calculate the perimeter of the circumference. In this present study, however, we will focus on the inner part of the circumference—the circle—as the basis for calculating capacity. Therefore, we will use the term ‘perimeter of the circle’ to specify or differentiate, and also because it deals with the inner part of the circumference, the available part of a sphere suitable for being filled, for example, with water. In this study, we will see that it is the circumscribed hexagon that has a side equal to the radius of the circle.
Keywords: Hexagon, Circumscribed, Radius.
Introdução
Segundo o site Mundoeducação, “se um hexágono regular está inscrito em uma circunferência, então todos os vértices do hexágono pertencem à circunferência. Além disso, o centro dessa circunferência coincide com o centro do hexágono, e o raio dessa circunferência possui a mesma medida que o lado do hexágono.” Desta forma, o perímetro do hexágono regular inscrito seria igual a 6 vezes o lado ou seis vezes o raio. O hexágono regular inscrito tem o lado igual ao raio da circunferência e o ângulo interno é igual a 60 graus, assim como o círculo tem um total de 360 graus. Dessa forma, o perímetro do círculo seria igual a seis vezes o raio ou três vezes o diâmetro.
Figura 1 – Círculo, Borda e Circunferência, Quadrado
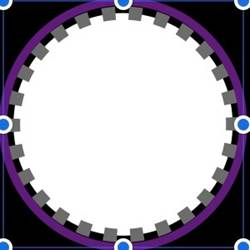
O círculo é a parte branca, a borda é a verde e pontilhada, a circunferência é a parte azul e o quadrado circunscrito é preto.
Figura 2 – Hexágono regular inscrito e circunscrito no círculo.
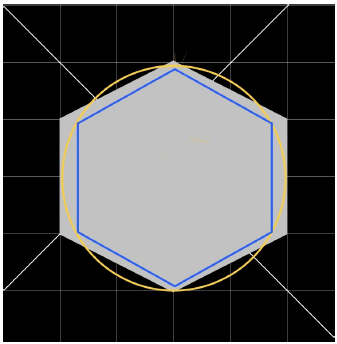
Vemos que no hexágono regular inscrito o seu lado é menor que o raio que corresponde a dois quadrados, mas o hexágono regular circunscrito tem o tamanho igual ao raio da circunferência. Assim temos:
Lado do hexágono circunscrito é igual a dois quadrados, logo o perímetro dele é seis vezes dois quadrados que somam 12 quadrados. O perímetro do circulo é igual a seis vezes o raio que também é dois quadrados totalizando 12 quadrados.
Sobre esse assunto, a Sociedade Torre de Vigia de Bíblias e Tratados diz: “A circunferência de 30 côvados é evidentemente um número redondo, porque, mais precisamente, seria de 31,4 côvados.
Neste respeito, Christopher Wordsworth cita certo Rennie como fazendo esta interessante observação: “Até o tempo de Arquimedes [terceiro século AEC], a circunferência do círculo era sempre medida em linhas retas pelo raio; e Hirão descreveria naturalmente o mar como tendo trinta côvados de circunferência, medindo-o, como era então invariavelmente costumeiro, pelo seu raio, ou semi diâmetro, de cinco côvados, que, sendo aplicado seis vezes em volta do perímetro, ou ‘borda’, daria os trinta côvados declarados.
Não havia, evidentemente, nenhuma intenção no trecho senão a de dar as dimensões do Mar na linguagem costumeira para que todos entendessem, medindo a circunferência do modo como todos os trabalhadores peritos, como Hirão, costumavam medir os círculos naquele tempo. Ele, naturalmente, porém, devia saber perfeitamente bem que, visto o hexágono poligonal assim circunscrito pelo seu raio ter trinta côvados, a verdadeira circunferência curva era um pouco maior.” (Notes [Notas] sobre a King James Version [Versão Rei Jaime], Londres, 1887) Assim, parece que a proporção de três por um (isto é, a circunferência tendo o triplo do diâmetro) era a maneira costumeira de expressar isso, visando-se que a medida fosse entendida como apenas aproximada.”
Figura 3 – Círculos de 3 (branco), 5 (amarelo) e 7 (azul) quadrados de aproximadamente 2,20 cm de diâmetro.
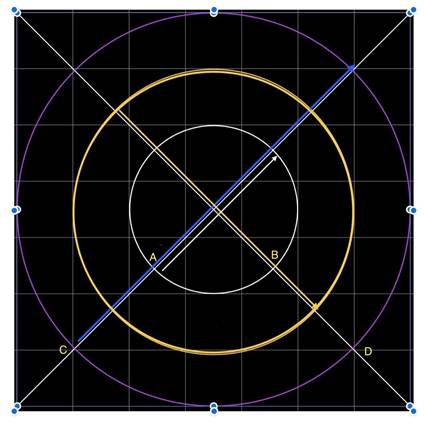
Figura 4 – Parte do círculo da figura 4 com régua na vertical medindo o raio dos círculos respectivamente 3, 5 e 7 quadrados.
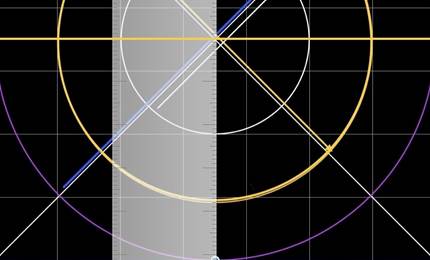
Ponto em que cruza a diagonal no círculo. Usaremos os Teorema de Pitágoras.

Círculo azul de 7 quadrados de diâmetro, aproximadamente igual aí 5 diagonais.
Seta Azul na figura 3.

Tamanhos do arcos na figuras 4 do circulo de 3, e 7 quadrados.
Arco AB é igual ao ¼ do perímetro do circulo de três quadrados.
3 quadrados vezes 3 é igual a 9 quadrados de perímetro.
9 quadrados de perímetro dividido por 4 é igual a 2,25 quadrados.
Arco CD é igual ao ¼ do perímetro do circulo de 7 quadrados.
3 quadrados vezes 7 é igual a 21 quadrados de perímetro.
21 quadrados de perímetro dividido por 4 é igual a 5,25 quadrados.

Parâmetros para o cálculo do volume e perímetro do círculo da esfera.
Perímetro do círculo da esfera é igual ao diâmetro vezes 3.
Esfera branca de 3 quadrados de lado tem o perímetro do círculo igual a nove quadrados.
Esfera amarela de 5 quadrados de lado tem o perímetro do círculo igual a 15 quadrados.
Esfera azul de 7 quadrados de lado tem o perímetro do círculo igual a 21 quadrados.
Atualmente a esfera azul com 7 quadrados tem como perímetro da circunferência igual a 22 quadrados. Sete x Pi = 22.
Arquimedes, matemático grego do terceiro século A.C que considerava o valor de Pi como único e proporcional ao diâmetro da circunferência e entre os valores 22/7< π < 223/71, conseguido através de divisões sucessivas dos perímetros de polígonos regulares inscritos e circunscritos.
O parâmetro acima de Arquimedes para cálculo de capacidade é conhecido mundialmente, mas não é o mais antigo. Arquimedes conseguiu o valor de Pi através de divisões sucessivas de polígonos regulares inscritos e circunscritos no terceiro século antes de Cristo.
O caso proposto neste estudo é por comparar o perímetro do hexágono regular circunscrito com o perímetro do círculo da esfera que é igual a três vezes o diâmetro. Este parâmetro para cálculo de capacidade da esfera foi mencionado por volta 580 A.C por Jeremias na antiga Judá, como escreve no livro bíblico de Primeira de Reis capítulo 7 e versículo 23, “Então ele fez o Mar, de metal fundido.
Ele era circular, com 10 côvados de uma borda à outra e 5 côvados de altura, e era necessário uma corda de medir de 30 côvados para dar a volta nele” e também por Esdras em 460 A.C provavelmente na antiga Jerusalém uns 120 anos depois. O templo construído por Salomão que continha essa bacia usada para armazenar água para os sacerdotes se lavar, o Mar de Cobre, foi inaugurado em 1026 A.C.
Conclusão
O que vemos na prática é que para cálculo de capacidade de esfera, atualmente se usam como parâmetro: Pi igual a 3,1428 ou 3,1415 ou 3,14 ou 3,1 ou 3 e as vezes as respostas são em função de Pi dividido por 3.
Como vimos acima, era adotado o conceito errado do hexágono como polígono regular inscrito sendo igual ao perímetro da circunferência, sendo que o correto é o hexágono regular circunscrito. Assim, conseguimos calcular o perímetro do circulo em números exatos, pois é obtido por multiplicar o diâmetro por três. Podemos constatar visualmente o cálculo do perímetro da circulo através das soma das duas transversais do quadrado circunscrito.
Referencias.
- – Biblioteca On-Line da Torre de Vigia. Estudo Perspicaz das Escrituras- Volume 2 páginas 301– https://www.jw.org/pt/biblioteca/livros/Estudo-Perspicaz-dasEscrituras/Mar-de-fundição-mar-de-cobre/ disponível em: 25/08/2025.
- – Biblioteca On-Line da Torre de Vigia.Tradução Novo Mundo das Escrituras Sagradas – Edição de Estudo. https://www.jw.org/pt/biblioteca/biblia/biblia-de-estudo/livros/1-reis/7/ disponível em 25/08/25.
- – Mundo Educação https://mundoeducacao.uol.com.br/matematica/relacoesmetricas-no-hexagono-regular-inscrito.htm disponível em 25/08/25.
- – SÍLVIO FILHO, José. Análise do volume do cubo e da esfera. In Ensino de matemática na atualidade:Percepções, contexto e desafio 3. Ponta Grossa. Aya Editora 2022. Pág 131-142.https://ayaeditora.com.br/wp-content/uploads/Livros/L136C12.pdf/ Disponível em 25/08/2025
- – SILVIO FILHO,José, Análise Geométrica ll- Estudo 9 página 104 Aya Editora(2023) https://ayaeditora.com.br/Livro/24333/ disposição em 25.08.25.
- – SILVIO FILHO, José. Análise do perímetro da circunferência. Artigo Revistas.com, volume 14, 2020. https://ayaeditora.com.br/wp-content/uploads/Livros/L136C12.pdf/ Dispositivo em 25/08/25.
